最小二乘偏移成像方法速度误差适应性测试分析

马方正 郭书娟

摘 要：为了适应高精度地震成像技术需求，实现了在反演理论指导下的最小二乘偏移成像技术。研究了最小二乘误差泛函建立，反偏移数据重构算法，及基于共轭梯度法的反演迭代更新方法等关键技术，建立了迭代最小二乘逆时偏移成像技术流程。用模型数据测试了最小二乘偏移的应用效果，并测试分析了当背景速度有不同误差时最小二乘偏移的收敛性和有效性，说明了当速度误差不同时最小二乘偏移的不同程度的优势。

关键词：最小二乘逆时偏移；迭代法；反偏移；共轭梯度法；速度误差

目前发展相对比较成熟的方法包括射线类、波动方程类等偏移成像方法可以实现复杂构造成像。但这些常规偏移算子是正演传播算子的共轭转置，而不是它的逆，由于采集孔径有限、地下模型复杂以及地震波带宽有限，主要侧重于實现反射界面的几何结构成像。为了适应越来越迫切的高精度储层刻画的要求，成像方法和技术的保真度需不断提高，简单的基于射线或波动方程的偏移成像理论不能支持进一步保幅成像的研究，需要地震反演方法理论的支持。基于反演理论的最小二乘偏移成像技术核心思想是求解模型空间的精确解，可以实现更加保幅和高分辨率成像，是地震成像技术理论由常规地下岩石的几何结构描述向更精细成像的推进和发展，是目前成像技术的发展趋势和研究热点。

Nemeth[1]提出了基于Kirchhoff的最小二乘偏移方法，Kuehl和Sacchi[2-3]提出了最小二乘裂步偏移算法，并于2002年提出最小二乘DSR偏移算法。

为了达到较好的成像效果，最小二乘偏移对背景速度场也具有较高的要求，当背景速度有误差时，最小二乘偏移的收敛性和成像效果都会受到影响。在实际资料处理时，速度误差不可避免，为了更好的指导最小二乘偏移在实际资料中的应用，建立了最小二乘逆时偏移方法技术实现流程，并结合模型数据试算说明了速度误差对最小二乘偏移方法技术的影响。说明了当速度误差不同时最小二乘偏移在提高分辨率和成像均衡性方面不同程度的优势体现。

2 最小二乘偏移对速度场误差适应性分析

在实际数据处理时，速度误差是不可避免的。若背景速度不合适，最小二乘偏移可能不会收敛至理想的情况。通过模型数据测试了当背景速度有误差时最小二乘偏移的收敛性和有效性。

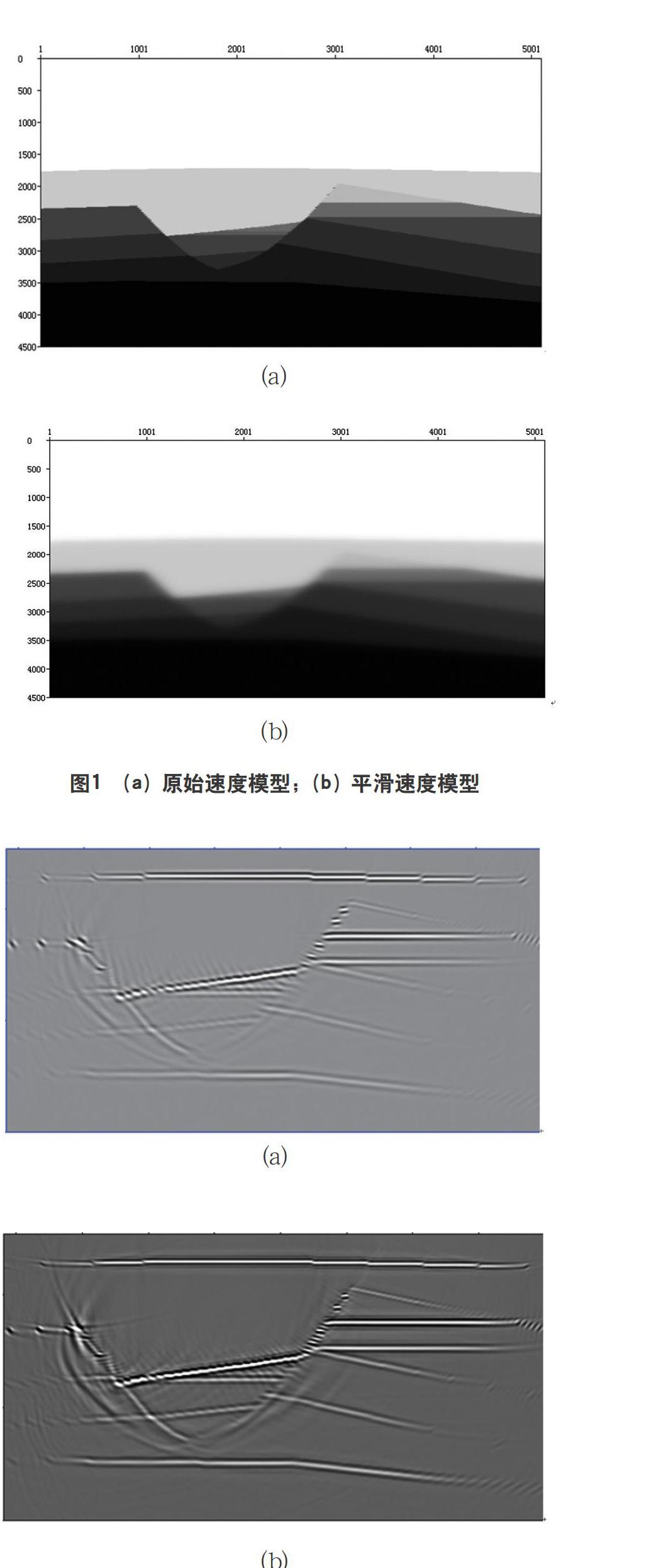
图1a是真实速度模型，图1b是用于偏移的背景速度模型。炮间距60m，道间距100m，最大炮检距是1500m，共150炮，每炮31道。

从此模型测试结果可以总结出，存在速度误差情况下，相较于初始偏移，最小二乘偏移普遍会有精度提高。但不同速度误差幅度，对比效果不同：（1）速度误差越小，速度场越精确，最小二乘逆时偏移收敛越快，在少数迭代次数内更好的收敛。而且最小二乘偏移相对于逆时偏移有比较明显的优势体现，如提高分辨率或者整体振幅均衡性；（2）若有较大的速度误差，即初始逆时偏移构造已经基本不准确的情况下，会致使最小二乘逆时偏移较低的收敛速度，相对于初始逆时偏移，最小二乘逆时偏移优势体现较弱。

3 结论与认识

实现了最小二乘逆时偏移技术，通过模型数据展示了最小二乘偏移在提高成像分辨率及提高了中深层成像精度方面的应用优势。并通过模型数据测试了当背景速度有误差时最小二乘偏移的收敛性和有效性。说明最小二乘偏移对速度误差也有一定的容忍度。但背景速度估计要尽量精确，在此基础上能够实现初始偏移构造成像基本准确，此时，继续做最小二乘偏移提高成像精度才更有意义。

【基金项目：国家重大科技专项（2011ZX05014-001-002）专题资助。】

参考文献

[1] Tamas Nemeth， Chengjun Wu?， and Gerard T.Least-squares migration of incomplete reflection

data[J]. Geophysics， 1999， 64（1）： 208–221.

[2] Kuehl H and Sacchi M D. Split-step WKBJ least-squares migration/inversion of incomplete data[A]. In：

5th SEGJ international symposium imaging technology，2001.

[3] Kuehl H and Sacchi M D. Least-squares wave-equation migration for AVP/AVA inversion[J].

Geophysics，2003，68（1）：262-273.