Hoek-Brown准则下岩质边坡稳定性的敏感性分析

2016-04-15■郑斌

福建交通科技 2016年1期

关键词：岩质岩体敏感性

■郑　斌

(中国电建集团华东勘测设计研究院有限公司，杭州　310000)

Hoek-Brown准则下岩质边坡稳定性的敏感性分析

■郑斌

(中国电建集团华东勘测设计研究院有限公司，杭州310000)

摘要针对胡克-布朗(Hoek-Brown)准则下的岩质边坡，克服传统极限平衡法的不足，提出了基于极限分析上限定理的敏感性分析方法。通过算例，进行某岩质边坡几何参数与强度参数对边坡稳定性的敏感性分析。结果表明，岩石抗压强度的敏感性始终等于1，而扰动系数的敏感性较小。岩石地质系数GSI的影响较小，而经验参数的影响最大。本文分析方法对边坡防护设计以及处治有一定的工程指导意义。

关键词边坡工程敏感性分析非线性破坏准则岩质边坡

1　引言

随着近年来我国基础交通建设的广泛开展，在高速铁路，公路的建设中，边坡工程的数量和规模也日益增多。对边坡工程的设计以及处治时，边坡稳定性指标是设计方案关注的首要目标，稳定性分析也是设计、施工中必不可少的首要步骤。

在稳定性分析中，除了对其安全系数、稳定系数以及滑动面分析进行分析和评价外，敏感性分析是非常重要的内容。通过敏感性分析，设计者可以了解不同物理参数以及强度参数对其稳定性的影响，从而在治理时设计有针对性的处置方案，从而降低工程成本，提供工程效率，以达到“花小钱，办大事”的目的[1-3]。已有学者对边坡的敏感性进行了研究，董瑞朝[4]在稳定性评价的基础上，对陕西凤凰山滑坡体进行了敏感性分析；杨春发[5]等人采用SARMA方法对刚果(金)SICOMINES铜钴矿矿区边坡进行了敏感性分析；罗常青[6]等人对加筋土质边坡进行敏感性分析等。

需要指出的是，已有的大多数研究均针对土质边坡进行。但实际工程中，很多山体边坡为岩质边坡。由于岩质边坡不符合摩尔-库伦准则(Mohr-Coulomb criterion),因此采用条分法等极限平衡方法进行敏感性分析已不大适用。所以有必要岩质边坡的敏感性分析方法进行讨论和研究。本文针对各向同性的遍布节理岩质边坡，采用上限分析方法，对其进行敏感性分析方法进行研究，并结合算例，表明了该方法的可行性。

2　敏感分析的基本原理

敏感性分析起初用于经济投资模型中，以评价不同经济指标对投资效果的影响。20世纪90年代，敏感性分析被引入到岩土工程的稳定性评价中，分析不用的物理力学参数对工程稳定性的影响。通过敏感性分析，设计者可以了解工程的各个参数对其稳定性的影响程度大小。若某因素对稳定性的敏感程度高，则称之为高敏感性因素。反之，则称之为低敏感性因素。充分了解某工程的高敏感性因素以及影响程度，对工程设计有重要的指导意义。采取针对性的处置措施，可以收到事半功倍的效果。例如，对于荷载敏感程度较高的工程，可采用分散其荷载的方法提高其稳定性；而对于土体强度较为敏感边坡，则可采用土体加固的方法进行处置。

具体到边坡工程，一般而言，其稳定性的影响因素可大致分为以下若干类：包括几何参数(坡角，高度)，一般物理参数(重度,弹性模量，泊松比)，强度参数(内摩擦角，粘聚力)以及外部条件参数(荷载，孔隙水压力等)。当边坡的稳定性用安全系数Fs进行表示时，其表达式可以写为：

第i个影响因素的敏感性可表示为

其中,Δxi为影响因素xi的变化值，ΔFs为该情况下安全系数Fs的变化值。η表示因素Xi在变量区间内对稳定性的影响程度。η越大,表明在该条件下Fs对xi越敏感。η为无量纲参数，不同因素之间的敏感性可以进行比较。在实际分析过程中，基准参数值xi一般由室内土工试验或者现场原位试验获得，参数变化量Δxi根据实际工程经验选取。

3　Heok-Brown准则及分析方法

由式(2)可知，敏感性分析的关键是边坡稳定性的求解。大多数已有研究中，研究者采用极限平衡方法(条分法)，对土质边坡进行稳定性求解，进而进行稳定性分析。条分法建立在静力平衡的基础上，并认为土体服从Mohr-Coulomb屈服准则。但是大多数岩质边坡由于节理面的影响，并不适用Mohr-Coulomb屈服准则。因此上述研究方法不适用于岩质边坡。事实上，除极限平衡外，目前常见的边坡稳定性分析方法还有极限分析方法。极限分析充分考虑土体塑性，更适合于土体等弹塑性材料的稳定性分析。且结合方法，可以更好地对遍布节理的岩质边坡求解。本文针对服从Heok-Brown的岩质边坡，采用极限分析原理对敏感性进行研究[7-9]。

极限分析采用上下限定理进行稳定性求解，应用上限法的关键在于构建破坏机构。本文采用对数螺旋线的旋转破坏机构，如图1所示。边坡坡脚为β，坡顶倾角为α。破坏机构的速度间断面为对数螺旋线BC，其方程为：

式中，rh，r0为对数螺旋线半径，θh，θ0为对应夹角，φ为土体内摩擦角。

在极限分析中，边坡稳定性一般由稳定系数Ns表示，其表达式如下：

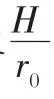
由下列式子表示：

上述对数螺旋线机构求解适用于服从线性Mohr-Coulomb准则的土质边坡。但是对于多节理边坡，其破坏准则表现出较强烈的非线性特征。加拿大著名学者E.Hoek在大量实验的基础上，考虑了岩体结构、强度等多种因素的影响，提出了适用于多节理岩体的破坏准则Hoek-Brown准则，此准则同样适用于含有均匀的各向同性结构面的岩体。

Hoek-Brown准则的表达式如下：

式中σ1，σ3是岩石的最大最小主应力，σ2是完整岩体的单轴抗压强度，D为岩石扰动因子，mi为完整岩块的Hoek-Brown常数，其中GSI根据岩体所处的地质环境，岩体结构特性和表面特性来确定。

由于Hoek-Brown准则中抗剪强度的包络线是非线性的，而上述破坏机构建立在线型Mohr-Coulomb破坏准则上。因此在计算Hoek-Brown准则下的岩体稳定性时，需要采用图2中所示的切线法[7-8]：

即在Hoek-Brown破坏包络线上任取一点C做切线，该切线与τ轴的截距为ct，其斜率为tanφt，其关系式可以写成：

任意切线的等效强度ct、φt均大于真实岩体强度，因此按切线强度计算的稳定系数为真实强度的上限解，同样也为真实荷载的上限解。

4　算例以及结果分析

极限分析中常采用Ns表示边坡的稳定性，因此在本文采用式(15)表示敏感性：

采用已有文献中的算例，分析设计参数对Hoek-Brwon准则下的边坡临界高度的敏感性。边坡的参数如下：重度γ=25kN/m3，σ=30MPa，β=35.5°，mi=2，D= 0.0，GSI=5。敏感性分析的结果如图3-图6所示。由于岩体扰动系数D与试验手段有关，且对岩土强度影响不大，故没有进行敏感性分析。

从图3可以看出，稳定系数随着岩体重度的增加大体上呈线性增大。当γ=20kN/m3时，敏感度大约为0.8，当γ增加至30kN/m3时，η也随之增加至1.2。增长速率大致为0.12。

从图4可以看出，稳定系数随着岩体GSI的增大而逐渐减小。当GSI=6时，敏感度大约为0.9，当GSI增加至15时，η也随之减小至0.6。GSI值较小时，其变化速率也逐渐降低。

从图5可以看出，稳定系数随着坡脚的增加而逐渐增大。当β=40°时，敏感度大约为0.5，当坡脚增加至70°时，η也随之增加至1.2。Ns随β基本呈线性增加。

从图6可以看出，稳定系数随着mi增加而逐渐增大。当mi=2.5时，敏感度大约为0.5，当mi增加至7时，η也随之增加至0.3。当mi≤3.5时，η的增加速率较大，当mi＞3.5时，η基本上呈线性增加。

综合图3至图5可以看出，参数γ，GSI，β以及mi对Ns的敏感性系数η均在0～3之间。对于γ，β以及mi，随着参数的增加η逐渐增加，而对于mi，η逐渐减小。其变化规律大体呈线性。就敏感性系数的大小而言，γ与β大致相等，GSI略小，而mi对Ns敏感性最大。而mi是反映岩石软硬程度的经验参数，适度注浆可增加岩体强度，从而有效提升岩质边坡的Ns值。