水下姿态测试系统运动的位置算法研究
2016-04-13郭华玲
陈 栋,郑 宾,郭华玲
(中北大学仪器科学与动态测试教育部重点实验室,山西 太原 030051)
水下姿态测试系统运动的位置算法研究
陈栋,郑宾,郭华玲
(中北大学仪器科学与动态测试教育部重点实验室,山西 太原 030051)
摘要:针对海洋探测中水下运动研究的需求,本文基于微惯导的水下姿态测试系统,介绍了该姿态测试系统的功能并分析其所搭载产品的运动情况,提出了一种针对水下运动载体的位置解算算法。
关键词:水下运动;姿态测试;位置解算
当今世界,海洋不仅是物流运输业的重要通道,更是一个有着富饶资源的宝库。随着对海洋[1]关注度的提高,将高科技应用到水下装备中是势在必行的。而为了更好地评价水下装备的性能,就需对水下装备运动中的姿态及运动轨迹进行研究。
1测试系统的功能
水下姿态测试系统[4]可以测试并存储载体运动过程中的三轴X、Y、Z的线加速度、三轴磁场强度和三轴角速度;内部自带的惯性传感部分可以根据测试参数自行解算出测试系统[2]的姿态角:俯仰角、横滚角和航向角。该测试系统具有体积小,精度高,功耗低的优点,可以安装在空间有限的各种载体或设备中,实现水下长时间工作,配置的数据采集存储模块可以收集保存数据,以备实验结束后回传数据,进行数据处理和分析。
2载体的运动过程分析及轨迹解算
某实验过程中,测试系统所搭载的产品搭载在载体上,利用测试系统来测试载体的运动姿态[5,6]和解算运动轨迹。载体的运动过程示意图如图1所示。
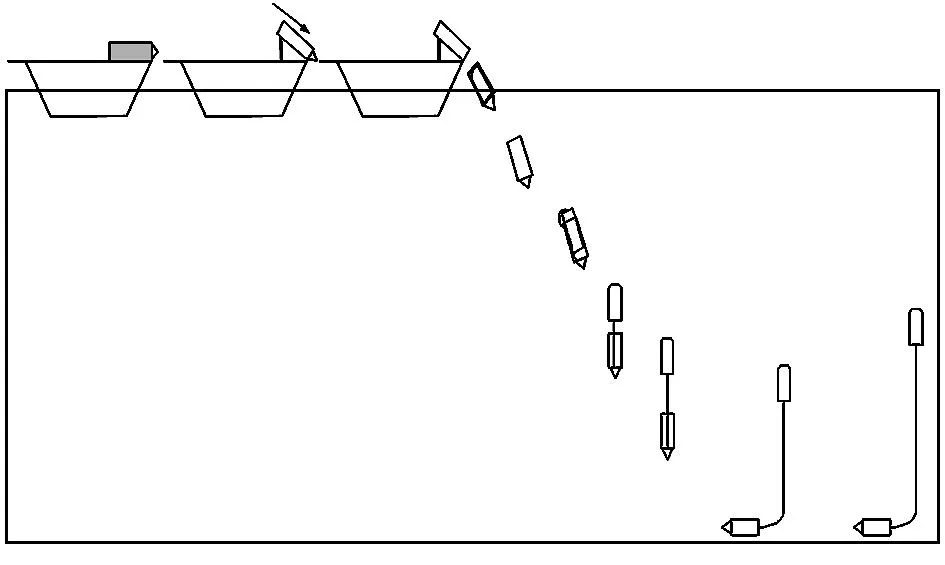
图1 载体的运动过程示意图
对整个运动过程分成三个阶段来分析。
2.1产品在布放装置中运动阶段
产品被装在保护壳体中,产品发射入水需要一定的角度,轨道升到一定角度后打开定位器,产品开始受到合外力而开始顺着布放装置向下滑动,滑出布放装置,做直线运动,记下此时的倾角θ的值。

图2 受力分析图
设置图中发射倾角θ=30°,产品受力分析情况如图2所示。忽略空气阻力的影响,产品在布放装置[5]中运动近似二维运动, 默认产品的轴线为X轴,垂直于轴线为Z轴图2中,产品受到竖直向下的重力mg,布放装置沿着Z轴对产品的支持力Fn,布放装置沿着X轴方向对产品的滑动摩擦力Fs,由于产品做初速度,加速度恒定的直线运动,所以将外力分别沿着X轴和Z轴分解,根据牛顿第二定律F=ma来求解加速度a。我们将重力分别分解为Gx和Gz,其中Gx=mgsinθ,Gz=mgcosθ。Z轴受力平衡,则X轴有:
F合=mgsin-Fs,从而我们可以得到产品的加速度,方向沿着X轴的正方向:
a=gsinθ-Fs/m.
(1)
在公式(1)中,Fs为滑动摩擦力,根据高中知识,滑动摩擦力等于最大静摩擦力,默认在整个运动过程中,摩擦力恒定不变。利用之前记录的产品初始滑动角度α,可以得到:
mgsinα=Fs.
(2)
所以根据公式(1)(2)得:
a=gsinθ-gsinα.
(3)
公式(3)中θ和α皆为产品的俯仰角,可以测试系统测得。由于我们需要研究产品的水平方向和竖直方向的轨迹,所以这里需要将加速度a分解成水平和竖直方向的两个分量ax和ay,那么产品沿水平方向做初速度为0,加速度为ax的匀加速运动,沿竖直方向做初速度为0,加速度az的匀加速运动:
ax=(gsinθ-gcosθ)cosθ.
(4)
ay=(gsinθ-gcosθ)sinθ.
(5)
为了使得整个运动前后衔接起来,在这里我们需要将水平和竖直方向组成的坐标系变换到导航坐标系中,这里采用常用的ENU导航坐标系[1](即东北天笛卡尔坐标系[9]):规定在当地水平面,地理东为水平X1轴方向,地理北为水平Y1轴方向,天为垂直于地面的Z1轴,姿态角分别为:航向角ψ为产品纵轴X轴与地理北方向的夹角,方向顺时针为正;俯仰角θ为产品纵轴X轴与当地水平面的夹角,方向是水平面上偏为正;横滚角λ为产品横轴Y轴与当地水平面夹角,方向是水平面上偏为正。
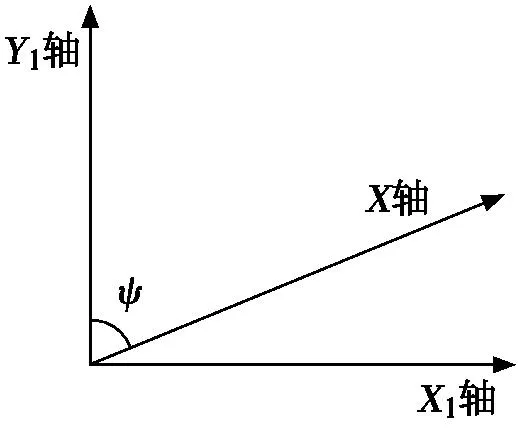
图3 加速度坐标变换示意图
图3中,航向角ψ的大小可以由测试系统测得,那么将产品水平放置时的轴向X轴分解到同一个水平面内的X1轴和Y1轴,加速度坐标变换示意图如图3所示。
那么导航坐标系的三轴加速度分别为:
ax=(gsinθ-gsinα)cosθsinψ.
(6)
ay=(gsinθ-gsinα)cosθcosψ.
(7)
az=(gsinθ-gsinα)sinθ.
(8)
所以可知产品在导航坐标系的三轴内做初速度为0,加速度恒定的匀加速运动,那么三轴的位移Sx、Sy、Sz分别为:
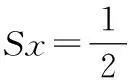
(9)
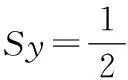
(10)
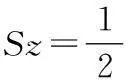
(11)
产品在布放装置中的运动距离为L,产品离开布放装置之前,做匀加速直线运动。根据公式(12)可以计算离开布放架时的速度,
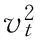
(12)
式中,vt为t时刻的速度,a为加速度,s为位移。根据上述角度参数和公式(12)我们可以得到产品离开布放架时三轴的速度:
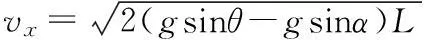
(13)
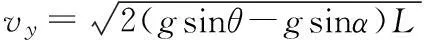
(14)
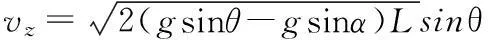
(15)
至此,我们得到了产品在离开布放装置之前的在导航坐标系三轴轨迹和三轴线速度。然后通过实验数据的解算[2,3]来验证算法的正确性,产品的各项初始参数为:θ=30°,ψ=45°,α=10°,L=2 m,经过计算得到如图4所示的在布放装置中运动的三个轴位移图。当产品离开布放装置时,X1轴速度为2.2 m/s,Y1轴速度为2.2 m/s,Z1轴的速度为1.8 m/s。

图4 产品在布放装置中运动的位移
2.2产品离开布放装置入水前的空中的运动过程
产品在空中的运动过程中,如果不考虑空气阻力的影响,那么物体在空中只受重力,产品做匀加速运动,但是由于产品的重心和形心不重合,所以产品在运动过程中会有转动,转动角度可以由测试系统的输出数据得到。
物体在空中做匀加速运动,X1、Y1和Z1轴方向的初始速度分别为产品离开布放架时的速度,水平方向不受力,所以物体在水平方向(X1和Y1轴)做匀速直线运动;竖直方向受重力,加速度为g,在竖直方向(Z1轴)做匀加速直线运动。从而我们可以得到产品在导航坐标系中的位移分别为:

(16)

(17)
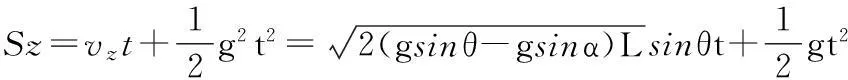
(18)
当产品离开布放装置时,产品的速度分为:X轴方向速度是2.2m/s,Y轴方向速度是2.2m/s,Z轴方向的速度是1.8m/s。空中的运动位移可以通过上面的公式测试得到。图5是空中三个轴向的位移图,从图5中可以看出在空中的运动高速为2m,X和Y轴运动距离均为1m,与实际情况相符。

图5 产品在空中运动位移图
2.3产品入水后轨迹的解算
当产品入水以后,由于水中环境复杂,产品受到多个力的作用做复杂运动,我们还是通过解算导航坐标系三轴的位移来分析。这里采用微元法[8]将运动过程分解为多个小段,以MTi[7]的采样周期每10ms当作一个小段来分析,在这段时间内产品近似做直线运动。位移分解图如图6所示,为了和前面的区分开,这里定义一些新的变量:L为入水深度值,ΔL为深度值的变化量,λ为产品的俯仰角,W水平为产品在水平方向的位移。

图6 每一小段运动位移分解图
图6中,当入水深度增加ΔL,俯仰角为λ时,水平方向的位移增量为:
W水平=ΔL×cot(λ) .
(19)
得到水平方向的位移增量后,通过航向角,将位移增加量分解到导航坐标系的X1和Y1轴中,得到:
Wx1增=ΔL×cot(λ)×sinψ.
(20)
Wy1增=ΔL×cot(λ)×cosψ.
(21)
当产品入水深度增加ΔL,通过俯仰角和航向角,可以得到X1和Y1轴的位移增量,入水深度从0开始,当深度为0时,X1轴和Y1轴的位移增量也为零,每隔10 ms,得到一个深度增量,相应的得到一个X1和Y1轴的位移增量,从而得到产品在水中的总位移。在t时刻的三个方向的位移可以由下面公式求得:
Wx1(t)=(L(t)-L(t-0.01))×
cot(λ)×sinψ+Wx1(t-0.0) .
(22)
Wy1(t)=(L(t)-L(t-0.01))×
cot(λ)×cosψ+Wy1(t-0.0) .
(23)
Wz1(t)=L(t) .
(24)
Wx1(0)=Wy1(0)=Wz1(0)=0 .
(25)
根据上面的四个公式可以依次求得产品在各个方向的运动轨迹。在这里由于深度传感器没装,所以没法得到深度数据,这里只对水下部分的算法做上述设计,这部分算法的验证还需要后期进一步来研究。
在产品轨迹的解算中,我们将运动过程分为了3个部分,每个部分分别计算出了在X、Y和Z轴方向的轨迹,因为我们在解算中选择的是同样的参考系,所以最后将这部分的轨迹加起来,就可以得到产品整个运动过程的轨迹。
3结束语
本文在对产品的运动过程进行了受力分析的基础上,分析了产品搭载的测试系统的位置的计算;在matlab环境下,根据水上部分的解算数据进行了部分仿真还原。结果显示符合实际情况,证明了算法的合理性,但是,水下情况还需要今后进一步来研究。
参考文献
[1]李江玲.海洋战略与爱国情怀[J].民生周刊(学术版),2013(7):100-103.
[2]郭晶晶.常用姿态测试技术的综述[J].山西电子技术,2013(5):87-89.
[3]刘浩,韩晶.MATLAB R2014a完全自学一本通(畅销升级版)[M].北京:电子工业出版社,2014.
[4]张文栋.存储测试系统的设计理论及其应用[M].北京:高等教育出版社,2002.
[5]李向楠.水下姿态解算的算法研究[D].太原:中北大学,2014.
[6]杜振宇,石庚辰.弹体飞行姿态测量方法探讨[J].探测与控制学报,2002(1):53-56+60.
[7]MTI User Manual//www.xsens.com.
[8]曹弋,杨忠振,左忠义.基于经典力学与有限元的交通事故再现分析法[J].中国安全科学学报,2014(10):42-47.
[9]施闯,赵齐乐,李敏,等.北斗卫星导航系统的精密定轨与定位研究[J].中国科学:地球科学,2012(6):854-861.
Research on the Algorithm of Moving Position for Underwater Attitude Measurement System
Chen Dong, Zheng Bin, Guo Hualing
(KeyLabofInstrumentationScience&DynamicMeasurement,MinistryofEducation,NorthUniversityofChina,TaiyuanShanxi030051,China)
Abstract:For the needs of underwater motion research in marine exploration, based on the underwater attitude test system of micro inertial navigation, the paper describes the function of this system and the movement of the product equipped with the system. A solution algorithm for the underwater location of moving carrier is proposed.
Key words:underwater sports; attitude test; location solution
中图分类号:TP202
文献标识码:A
文章编号:1674- 4578(2016)01- 0080- 03
作者简介:陈栋(1988- ),男,山西吕梁人,硕士研究生,研究方向:动态测试与智能仪器。
收稿日期:2015-09-23
