概化理论和EduG在教育测量研究中的应用——以试题难易度分析为例

王天剑，彭中梅

（1. 贵州财经大学 外国语学院，贵州 贵阳 550004；2. 贵州财经大学 图书馆，贵州 贵阳 550004）

概化理论和EduG在教育测量研究中的应用
——以试题难易度分析为例

王天剑1，彭中梅2

（1. 贵州财经大学 外国语学院，贵州 贵阳 550004；2. 贵州财经大学 图书馆，贵州 贵阳 550004）

概化理论是一种重要的现代教育和心理测量理论。它整合了方差分析与传统的真分数理论，形成一种新的测量信度评价技术。为了掌握概化分析技术，讨论了概化分析中的基本概念，并以一个试题难易度测量程序研究为例，介绍了利用软件EduG进行概化分析的基本程序和方法。

概化理论；EduG；教育测量

概化理论（Generalizability Theory， GT）是评价行为测量信度（reliability）的理论[1]。它整合了经典测量理论（Classical Test Theory）与方差分析技术（Analysis of Variance），形成一种现代测量评价理论[2-4]。依据经典测量理论，观测分数是真分数与随机误差之和（X = T + E）。真分数是测量特质的真值，随机误差是测量中的所有偏差[4]。随机误差源于哪些因素？为探索这一问题，概化理论整合了方差分析的概念，将随机误差区分为不同的来源成分，估算各自所占权重，并计算信度系数，反映测量的精准度[5]。基于概化分析，研究者不仅能评价既有测量程序之优劣，也可以探索测量程序优化之方案。概化理论在国外教育与心理测量中极受重视。美国心理学协会、教育研究协会和教育测量委员会联合颁布的《教育和心理测量标准》（Standards for Education and Psychology Testing，AERA，2002）明确要求，在建立观察和测量程序的信度与效度时，需依据概化理论[6]。根据对2000-2014年间8种SSCI期刊的综述，邱均平等指出，美国教育评价理论研究的三个热点中含有概话理论（其余两个是项目反应理论和经典测量理论）[7]。

学校的一般测试都属于教育测量范畴。近年来，国内已有学者开始借助概化理论进行相关研究。徐鹰等使用概化理论，考查了高考英语听说模拟测试和CET作文评分程序的信度[8-9]；关丹丹从概化分析视角，研究了阅读理解测试的信度[10]；基于概话理论，温红博等检查了义务教育阶段学生识字量测试的信度[11]。这些研究披露了测量程序中存在的各种缺陷，对于改进测量设计具有重要参考价值。

教育测量贯穿教学的始末。从平时测试、期末测试、升学测试，到各种竞赛测试等，无不需要采用具有较高信度和效度的测量程序。利用概化理论对测量数据进行分析，对于提高测量信度具有重要意义。鉴于国内关于概化理论应用方法和操作入门的研究尚且有限，本文在描述概化分析基本程序的基础上，以试题难易度分析为例，简要介绍利用工具软件EduG进行概化分析的步骤（EduG系瑞士教育专家Jean Cardinet指导下开发的概化分析免费软件，可从如下网页下载：http：//www.irdp.ch/ edumetrie/englishprogram.htm）。

1 概化分析的基本程序

1.1 确定观察设计与估计设计

概化分析涉及的变量（测量的对象以及构成测量条件的因素）统称侧面（facets）。观察设计是指侧面之间的结构关系，主要包括交叉关系、套嵌关系及其各种组合派生的复杂关系。交叉关系是指每一个侧面的每个水平，与其他任一侧面的每个水平均存在接触。套嵌关系是指一个侧面的不同水平仅与另一个侧面的一个水平结合。当有三个或者更多侧面时，会存在复杂的交叉套嵌关系，如先交叉后套嵌，先套嵌后交叉，或者层层叠加套嵌。例如测量中的被试为10名学生（S），评分者为2名教师（R），这时学生和教师就是两个侧面，其水平分别为10和2。倘若每个学生均需要接受每个评分员评分，即S和R的各个水平均有结合，则两侧面构成交叉关系（表示为S×R，或者SR）。这样可以产生10 × 2 = 20个数据。倘若5名学生接受一名评分员评分，其余5名学生接受另外一名评分员评分，即S的5个水平与R的一个水平结合，S的其余5个水平与R的另一水平结合，这时两个侧面存在套嵌关系，S套嵌于R之内（表示为S：R）。这样可以产生1× 5 + 1×5 = 10 个数据。如果再介入一个试题侧面I，则会存在SRI（三侧面完全交叉），S：RI （RI交叉，S套嵌于RI），SR：I （SR交叉，SR套嵌于I），或者S：R：I （S套嵌于R，R进一步套嵌于I） 等复杂关系。

估计设计是指规定各个侧面是以多少个水平估计多大的总体（Universe）。它包括三种类型：（1）侧面总体固定，总体的各个水平全部出现在研究中；（2）侧面总体固定，以随机方式抽取的总体的部分水平出现在研究中；（3）侧面总体无限大（INFINITE，或者INF），以随机方式抽取的总体的部分水平出现在研究中。不同的估计设计研究结果具有不同的概化程度。第一种类型的研究结果仅适用于研究中涉及的侧面的特定水平，这类模型叫做固定模型；第二种和第三种类型的研究结果在理论上可以概化到总体的所有水平中，这两类统称随机模型。一个研究程序中可以同时容纳不同类型的设计成分，这样的模型叫做混合模型。

1.2 确定测量设计

测量设计是指确定哪些侧面是区别侧面（Differentiation Facet），哪些是工具侧面（Instrumentation Facet），测量性质是相对的，还是绝对的。区别侧面是测量的对象，工具侧面是构成测量条件的因素。在教育研究中，一般情况下区别侧面就是学生，我们倾向于关注学生的测试结果是否稳定可靠。其他因素大多属于工具侧面，它们是为学生的测试服务的。但是基于研究兴趣，我们也完全可以将区别侧面和工具侧面调换位置。例如，在一个由学生（S）、评分者（R）和试题（I）组成的交叉设计（SRI）中，如果旨在考查学生的成绩是否可靠，则区别侧面为学生，其余因素构成工具侧面（表示为S/QR）；如果旨在检查学生在不同试题上得分高低的稳定性，则区别侧面是试题，评分员和学生变成工具侧面（Q/ SR）；如果旨在检查不同评分员给分差别是否稳定，则评分员成为区别侧面，学生和试题构成工具侧面（R/SQ）。

为了将学生（或其他研究对象）排名进行的测量叫做相对测量，为了考查学生（或其他研究对象）是否达到既定标准的测量叫做绝对测量。例如竞赛、拔尖、择优之类的测试均为相对测量，目标测试、掌握性测试、过级测试、毕业测试等一般均视为绝对测量。之所以确定测量的性质是相对的还是绝对的，目的在于选择对应的信度系数计算方法，并对结果做出正确的解释。

2 概化研究举例

借助软件进行概化研究非常简便。现以一组试题难易度分析为例，展示利用软件EduG进行概化分析的方法。

2.1 问题描述

现有从题库中随机抽取的10道英语语法题，为了确定其相对难易度，校方进行了一项测试研究。受试者为80名初三学生，其中40名随机抽自普通班，40名随机抽自重点班。为了控制试题的顺序效应，10道试以两种版本（A卷和B卷）呈现，其间唯一的差别是随机排列顺序不同。重点班和普通班各有一半（20名）学生做A卷，一半学生做B卷。每道题做对计1分，做错记0分。每道题的难易度以通过率为考查指标，通过率越高越容易。例如，80名受试者中，有70名作对的题目，难易度为：70 / 80 = 0.875。由于每个学生都要完成10道题，80个学生可产生800个原始数据。试根据这些数据，利用概化理论回答如下研究问题：

1）哪些因素对试题得分影响较大？

2）这种测量程序是否能准确估计不同试题的难易度？

3）重点班与普通班在10道题上的平均得分是否类似？

4）试题呈现顺序对难易度有影响吗？

5）试题的难易度顺序在重点班与普通班之间是否有别？

如上问题中，最核心的是测量程序能否准确估计不同试题的难易度，其他属于附带性问题。

2.2 问题分析

2.2.1 观察设计

本例共有四个侧面：班级（Class或C），试卷版本（Version或V），试题（Question或Q）和学生（Student或S）。试题同班级、版本和学生等三个侧面构成交叉关系，因为同样的试题被包含在不同的版本中，提供给每个班级的每个学生；班级同版本也构成交叉关系，因为每个班级都要接触不同版本的试卷；学生套嵌于班级和版本内（Student within Class and Version，S：CV），因为班级和版本交叉后构成四种条件：重点班-A卷，重点班-B卷，普通班-A卷，普通班-B卷，每种条件内“套嵌”20名学生。整个测量的观察设计为：（S：CV）Q，即班级和版本交叉，学生套嵌于班级和版本的交叉单元内，学生、班级和版本同试题构成交叉关系。

2.2.2 估计设计

本例中班级为固定侧面，水平为2，全域为2，因为研究者面对的班级类型仅有两个水平：重点班和普通班，且两个水平均进入了测量程序。试卷版本水平为2，全域为无限，因为两个版本仅代表两种试题排列顺序，实际上10道试题通过不同的排列组合，可以组成大量（1010）的可能版本，由于数量过大，版本全域可视为无限。试题的水平为10，全域为无限，因为10道试题仅为样本，它们取自题库，而题库可视为一个无限总体。学生尽管有80名，但套嵌于每个“班级-版本”单元内的水平数为20。因为学生是从无限总体中抽取的，其全域为无限。表1呈现的是观察和估计设计结构。

表1 观察和估计设计表（INF = Infinite）

2.2.3 测量设计

本例着重考查测量程序对试题难易度测量的准确度，因此试题是区别侧面（即研究对象），班级、版本和学生为工具侧面（测量的条件因素），这种关系可以表示为Q/CVS。由于研究者关注的焦点是程序对试题难易度测量的准确度（各道题测出的通过率是否准确可靠），测量是绝对的（解释结果时，需要观察绝对指标）。

2.3 输入程序指令

为了利用EduG进行概化分析，需打开软件，并在界面中按如下方式填写指令（见图1）。

图1 概化分析指令界面

完成如上指令的具体步骤包括：

1）确定文件名称与保存位置。运行软件，依次点击File和New，在弹出的界面中填写文件的存储名称和位置（本例名称取“Analysis of question difficulty”，保存位置为F盘）。

2）打开文件，在界面中填写相关指令。

ⅰ在Title后填写文件的标题（这是分析报告中使用的标题，本例仍然用“Analysis of question difficulty”；

ⅱ在Number of facets后选4，表示分析涉及四个侧面；

ⅲ参照表1，在Observation and estimation designs之下填写各侧面的英文名称（EduG不能准确识别汉字），名称的字母代码（C，V，S：CV，Q）。填写各侧面的水平（2，2，20，10），各侧面的全域容量（无限表示为INF）；

ⅳ在Measurement design 后填写测量设计代码（Q/CVS）；

ⅴ在Reports下勾选RTF（表示输出的结果以Word表格形式呈现）；

ⅵ其他选项保持默认值①。

ⅶ插入数据。点击Insert data，选择scores，即弹出数据录入界面（图2）②。第一列表示的是班级序号，第二列是版本序号，第三列是学生序号，第四列是问题序号。前四列是软件根据观察设计自动生成的，第五列（Data）是需要我们录入数据的位置。原始分数共计800个，可以依次录入表中（从重点班内，做A卷的第一个学生，在第一道题上的得分开始，循序录入）。

2.4 查看结果

录入如上程序指令和数据后，点击Compute，即可查看结果。如下部分将结合研究问题呈现相关结果。

1）哪些因素对试题得分影响较大？

表2是输出的方差分析结果。各列依次表示对试题总分变异具有潜在影响的因素（侧面及其交互）、平方和、自由度、均方、随机效果模型方差成分、混合效果模型方差成分、Whimbey’s矫正的方差成分、各矫正成分的百分比及各随机效果模型方差成分的标准误。根据表2第一列和第八列可知，有四个因素对试题总分变异影响较重：

SQ：CV（学生、试题的交互作用）为61.6%；Q（试题）为17.0%；S：CV（学生）为 13.6 %；C（班级）为6.6%。

学生和试题的交互作用意味着，不同学生在不同问题上得分或失分的倾向存在反差。需要注意的是，未知因素和随机因素的影响与SQ的交互作用是混合在一起的，所以其分量较大（61.6%）。试题和学生对总分变异的影响居中（分别为17.0%和13.6%），班级类型的影响较低（6.6%）。需要注意的是，当方差成分接近零时，在计算中会出现负值（理论上的无效值），这些数值在后续处理中视为0。表2中的V、CVQ的方差成分均属此类情况。

2）这种测量程序是否能准确估计不同试题的难易度？

表3呈现的是概化研究表（G-Study Table）。其中第一列是研究对象，即区别侧面（本例是指试题），第二列是区别侧面的方差（相当于经典测量中真分数解释的变异，这里可理解为 “试题可以解释的得分变异”），第三列是潜在的误差来源，第四、五列为相对误差方差及其百分比，第六、七列为绝对误差方差及其百分比（注意：由于班级C为固定侧面，不存在随机抽样误差，故该侧面及其交互作用对测量误差的影响为零）。各列数据是进一步计算概化系数（相当于信度系数）的基础。当系数大于或等于0.80时，一般认为测量结果准确度比较理想[12-13]。

由于本例属于绝对测量，需要根据绝对概化系数（ Coef_G absolute）判断测量的准确度。这里Coef_G absolute = 0.94 ＞ 0.80，表明测量结果可靠准确，即程序能够准确估计不同试题的难易度或者通过率。这里的0.94也意味着，使用该程序测量试题难易度，误差造成的影响仅有6%（误差可解释总分变异的6%）。

表2 方差分析表

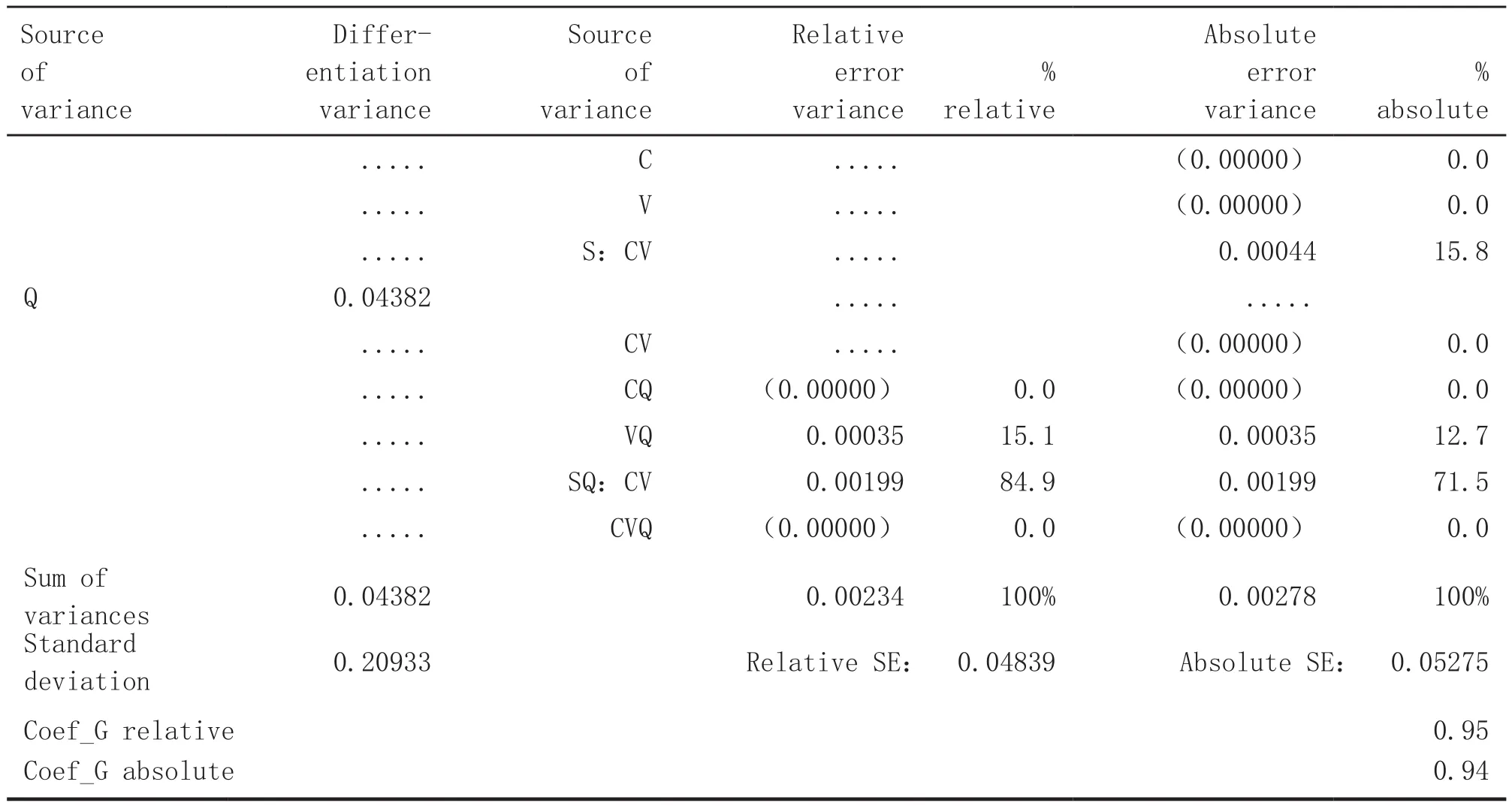
表3 概化研究表

3）重点班与普通班在十道题上的平均得分是否类似？试题呈现顺序对难易度是否有影响吗？

回答这两个问题，需要观察有关方差分析结果和均分。方差分析结果（表2）显示，班级（C）的均方（MS）为 14.31，对试题总分变异的影响权重为6.6%，版本（V）的均方为0.10，对试题总分变异的影响权重为0。据此可以初步推断，班级侧面对试题得分有一定影响，但试题呈现顺序对试题得分（难易度）影响不显著。

不同班级和版本的均分（Mean）差别是否显著？为了获取均分，需在EduG软件指令界面中，点击Mean，在弹出界面中选择C（班级），或者选择V（版本），然后点击Compute，即可获得重点班、普通班、A卷和B卷的平均分（见表4）。过率为39 %）。A卷和B卷的平均分差别不明显：A卷的均分约为0.51（通过率约51 %），B卷的均分约0.54（通过率约54 %）。

综合上述方差分析和均分结果可以推论：班级侧面对试题得分有一定影响，重点班的均分明显高于普通班；不同的呈现顺序对试题得分（难易度或者通过率）影响不明显。

3 结语

表4 不同班级或版本均分

概化理论是将方差分析与传统的真分数理论整合发展而来的信度理论，它是现代教育和心理测量的重要理论之一。利用概化理论，我们可以对考试中的不同因素（如试题、受试者、评分者、考试条件等）进行研究，了解不同因素对测量结果和测量准确度的影响，评价测量程序的可靠度和测量结果的稳定性。本文简要讨论了概化分析中的观察设计、估计设计、测量设计等基本概念，并以试题难易度测量程序研究为例，介绍了利用软件EduG进行概化分析的步骤，以及对输出结果的解释方法。囿于篇幅，只能涉及部分功能和用法，希望有助于概化分析技术的推广。

平均分是指每人每题平均得分。由于做对一题得1分，做错得0分，每人每题的平均分介于0～1之间。全部做错均分为0，通过率为0 %；全部做对均分为1，通过率为100 %。根据表4可知，重点班和普通班在十道题上均分差别明显：重点班均分约0.66（通过率约66 %），普通班均分为0.39（通

注释：

① Number of decimals 表示结果中小数位数；Decimal separator 表示小数的分隔符号；Estimate of Phi用于绝对测量；Optimization和G-Facets analysis用于优化设计研究。如关心均值，需点击Mean并勾选相应侧面。

② 如有现成的原始数据（或平方和），点击Import file with raw data（或Import sums of squares）；如需浏览或编辑既有数据，点击Brows/Edit data；导出数据点击Export data；删除数据点击Delete data。

[1] Shavelson R.J., Webb N.M. Generalizability theory: A primer [M]. California: Sage Publications Inc., 1991： 1-55.

[2] Cronbach, L. J., Rajaratnam, N., & Gleser, G. C.. Theory of generalizability: A liberalization of reliability theory[J]. British Journal of Mathematical and Statistical Psychology, 1963（2）：137-163.

[3] Cronbach, L. J., Gleser, G. C., Nanda, H., et al. The dependability of behavioral measurements: Theory of generalizability for scores and profiles[M]. New York：Wiley, 1972：7-43.

[4] Brennan, R. L.. Generalizability theory[M]. New York：Springer, 2001：3-14.

[5] Cardinet, J., Johnson, S., Pini, G.. Applying generalizability theory using Edug[M]. New York, NY： Taylor & Francis Group, 2010：6-20.

[6] American Education Research Association （AERA）, American Psychological Association（APA）, National Council on Measurement in Education （NCME）. Standards for education and psychology testing[M]. Washington，DC：American Psychological Association, 2002：15-17.

[7] 邱均平，欧玉芳. 美国教育评价研究的知识基础与热点[J]. 中国地质大学学报（社会科学版），2016（3）：142-149.

[8] 徐鹰，曾用强. 基于概化理论和多层面 Rasch模型的计算机化英语听说考试评分研究[J]. 电化教育研究，2015（3）： 89-95.

[9] 徐鹰. 概化理论和多层面R asch模型在CET- 4作文评分中的应用研究[J]. 西安外国语大学学报，2016（1）：91-95.

[10]关丹丹. 阅读理解测试的信度研究： 来自概化分析的视角[J]. 心理学探新，2016（1）：70-74.

[11]温红博，等. 基于概化理论的识字量测验测试用字数研究. 语言文字应用，2016（1）：74-84.

[12]靳雪莲，滕金生，杨德山. 网络论坛公共事务讨论语言的修辞特征和成因[J].重庆邮电大学学报（ 社会科学版），2014（5）：117-123.

[13]翟洪昌，徐小霞，俞园. 房产销售人员职业锚类型与工作满意度的关系研究[J]. 文山学院学报，2013（3）：72-77.

The Application of Generalizability Theroy and EduG to Measurement in Education: Illustrated with a Study of Test Item Dif fi culty

WANG Tianjian1, PENG Zhongmei2
(1. School of Foreign Languages, Guizhou University of Finance and Economics, Guiyang 550004, China; 2. Library, Guizhou University of Finance and Economics, Guiyang 550004, China)

Being one of the most important modern measurement theories in education and psychology, generalizability theory combines ANOVA and traditional True-Score theory, and develops a new technique for the evaluation of reliability. To help readers grasp the skill of generalizability analysis, this paper discusses the fundamental concepts in it, and employs an example of test item dif fi culty study to illustrate the basic steps involved in generalizability analysis with the software EduG.

generalizability theory; EduG; application

G449

A

1674-9200（2016）06-0088-06

（责任编辑 杨爱民）

2016-03-10

贵州省科学技术厅、贵州财经大学软科学研究联合基金资助项目“贵州省软件产业进入国际市场的终端用户许可协议设计研究”（黔科合LH字〔2014〕7262）。

王天剑，男，河南南阳人，贵州财经大学外国语学院教授，博士，硕士生导师，主要从事教育测量学研究；彭中梅，女，河南南阳人，贵州财经大学图书馆馆员，主要从事图书资料管理研究。