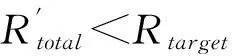一种新型低复杂度的OFDM自适应调制算法*

方四祥

(解放军理工大学 通信工程学院,江苏 南京 210007)



一种新型低复杂度的OFDM自适应调制算法*

方四祥

(解放军理工大学 通信工程学院,江苏 南京 210007)

摘要：OFDM自适应调制最经典的三大算法Hughes-Hartogs算法、chow算法、Ficher算法虽然在信道利用率方面具有无与伦比的优势，但其需要非常大的计算复杂度，对现如今高速通信的要求显然是不符合的；随着对该技术深入的研究有相关学者提出了子带的划分，比如这些算法有SBLA算法、NUDS算法、IDS算法这些技术虽然降低了系统的迭代复杂度，但牺牲了更多的信道容量资源为代价的，利用Ficher算法原理，提出了一种新的子带划分算法，其兼顾了算法的复杂度也能尽可能的逼近不进行子带划分时的信道利用率，通过仿真结果说明了这一点。

关键词：OFDM系统；子带划分；信道容量；自适应调制技术；误比特率

0引言

OFDM因其各子载波具有正交性，且子载波的频谱具有相互重叠的性质，相比于传统的频分复用具有更高的频谱利用率，其另一个优点是对频率选择性衰落信道具有很好的抑制作用。自适应调制手段可以根据当前的信道状况实时改变各子载波的发射功率、调制类型和编码方式，可以极大的提高频谱资源和信道的容量。而且对于功率效率也能显著的提高。其成为现在现今非常重要的OFDM技术研究的方向之一[1-2]。

自适应调制方面经典的算法有Fischer算法、chow算法、注水算法和Hughes-Hartogs算法[3-5]，同时，随着对OFDM研究的深入，学者们又提出了许多改进的算法。但上述列举的算法均是以子信道为基础进行的功率和比特分配，这样的缺点是计算复杂度高，不能满足于现今高速通信的要求。为了克服这种缺点，目前已经有一些文献对于此问题进行了改进---提出了基于自带划分的自适应算法[6-8]。这类算法的思路是将每个OFDM符号按一定标准划分为自带且对于同于自带内的子载波才用一样的的功率和比特分配。但对于自带的划分具有严格的要求，即对于划分后的自带宽度不得大于信道相关带宽。其中关于固定门限的子带划分算法(simple block loading algorithm,SBLA)是典型的子带划分算法[9],该算法的思路是：其子带的宽度是固定的，比特分配的原理是于预先设定的门限进行比较，这种算法的复杂度低，可以快速的更行自适应调试参数。对信道有很好的跟踪能力；本文要介绍的低复杂度的OFDM自适应调制方法，其子带划分的带宽是根据子载波的所处的信道状况实时变化的。这样的好处是，对比于机械的固定子带宽度而言的自适应方法，这种子带划分能更好的拟合信道的状态曲线，也即更接近于不进行子带划分时的自适应系统性能[10-11]。因此，本文经过综合了SBLA算法以及动态子带划分自适应调制算法的优点提出了一种低复杂度的OFDM自适应调制算法(an low computation complexity adaptive modulation algorithm of OFDM,简称LCC算法)，该算法可以依据信道的状态信息不需要迭代就能完成子带的划分，利用这种算法进行比特的预分配，可以降低后续比特的迭代调整次数；在比特调整时充分利用信道条件好的子带。这样既能保证系统的性能，也有相当可观的计算复杂度。仿真结果刚好证明了这点。

1自适应OFDM调制系统模型

其模型如下图1所示[12]，首先通过信道估计[13]获得信道的频率响应，然后将这些信息反馈到发送端，通过下文讲述的自适应调制算法来控制发送端在各个子载波上的比特分配和功率分配，同时将这些信令信息传输到解调端，从而让接收端采用正确的解调方式进行解调，来完成响应的数据恢复。为了能在接收端正确的解调必须要求对这些信令信息高效、可靠的传输。

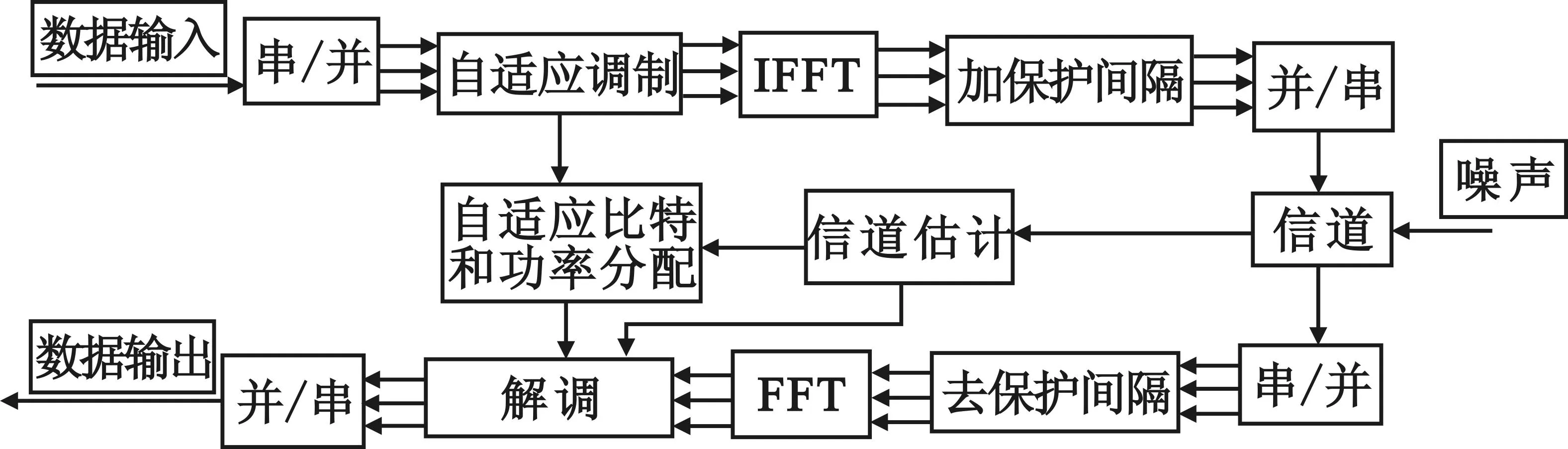
图1　单个用户OFDM自适应调制系统框

2LCC算法

LCC算法的优化方案是基于最大比特率准则，也就是满足下列表达式：

pT=Pi,BER≤BERt,

(1)

式中，Pt是目标功率，BER是目标误码率。本文介绍的算法首先是依据子载波的信道响应以此来实现子带宽度的划分。

2.1自适应调制算法子带的划分

将频率选择性衰落的信道划分为N个子信道，假定在这些子信道中信号是平坦衰落的，在接收端定义子载波j的信噪比为：

(2)

式中，H(j)是子载波j的频率响应，且j取值为1,2,…,N,σ2为子载波的噪声功率。

在文献[14],由信道的频率响应，N个子载波可以划成K个子带：

(3)

由下面的式子求出各个子带中含有的子载波数目：

(4)

第t个子带的宽度(即子带包含你的子载波数目)为bi，其中i=1,2,3,…,N，在第i个子带内的子载波可以用t(i)表示，i=1,2，…bi。因此，信道频率响应可以由式(3)和式(4)得出，可以看出无需再次循环迭代就能就能进行子带的划分，所以，在计算量上有非常可观的降低复杂度。

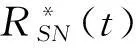
(5)

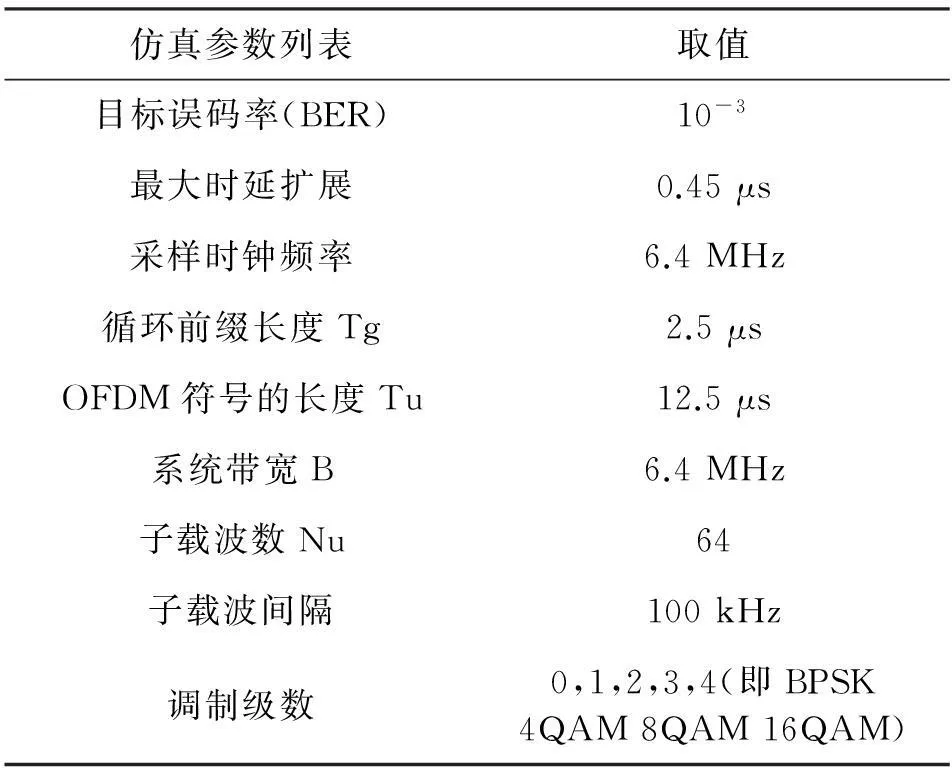
式中，RSNt(s)表示的是第t个划分子带上第s个子载波位置的信噪比。在该文献得出，采用“随机信噪比选取的方案”要比通常的“子带最小增益方案”、“算数平均值方案”具有更低的算法复杂度，且对整个系统的性能没有太大的影响。文章中定义了第t个子带的第i个子载波的等效信噪比：

(6)

2.2算法的流程

通过在上一节子带划分完成后，将子带按对应信道信噪比值按从小到大的顺序排序。此后，按照SBLA算法给各子载波分配一样的比特，完成比特的初始分配；接着依据下述算法流程对各子带的比特进行调整。比特调整的思路是优先利用等效信噪比差值较大的子带。算法的具体流程如下所示。

(1)算法的初始化，假设OFDM符号总的子载波数为K，平均每个子载波携带的比特数m,则每个OFDM符号含有的总的比特数Rtarget=mk。

(2)各种调制方案的门限值为RSNstd(j)，其中j的取值范围0～4代表不同的调制级数。

(3) 由各个子载波频率响应H(i),由文献[14]给出的式(3)和式(4)可以计算出OFDM符号子带的数量N和子带的宽度b。

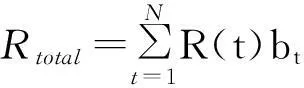
(i)如果R″total=Rtarget,则算法跳转到(8),进行功率分配。

(ii)如果R″total>Rtarget，则再次跳转到步骤(6)。继续减少子带上比特的分配。

(iii)如果R″total

(7)如果Rtotal

(8)功率P在发射端上的子载波上平均分配。

3结果仿真与分析

3.1系统仿真参数

本文仿真的OFDM参数如表格1所示。系统调制级数 的范围在0,1,2,3,4，其对应可选择的调制方式为0，BPSK，4QAM，8QAM，16QAM。本文设定的OFDM符号携带的比特数目128 bit。每个OFDM符号的子载波数是64，在多径信道下仿真。

表1　OFDM系统仿真的参数

图2是在上述参数的OFDM系统的仿真，从该图可以看出每种调制方式在目标误码率(10-3)时的信噪比数值，即BPSK、4QAM、8QAM、16QAM对应的信噪比门限RSNstd/dB值分别是17.1、22.3 25、27.8。

图2　不同调制级数(方式)时OFDM系统误码率曲线

3.2算法的复杂度分析

在如表3中列出了Chow算法、LCC算法、SBLA算法在算法计算时所必须的乘法次数、比较次数和对数次数。明显可以看书子载波数K、自带数目N和设定的目标比特数目Rtarget是决定LCC算法、SBLA算法的主要因素，假定子载波数目K和Rtarget不变，则子带数N是决定复杂度的重要变量，且是正相关的关系。SBLA比本文描述的算法复杂度更低，SBLA和本文列出的LCC算法都是以子带为基础进行的比特分配，而chow算法是以子载波为基础的比特分配，所以后者的复杂度是最高的，表2是具体的复杂度比较。

表2　比较算法复杂度

图中符号含义：信噪比门限数目L;自适应算法的比特调整次数count;Chow算法的最大迭代次数

3.3算法仿真的分析

本文描述算法在3.1节的OFDM系统中完成LCC算法的仿真并对此作出相应的分析。在每次仿真中，设定发送2 000个OFDM帧，每个OFDM帧包括30个OFDM符号。本文描述的算法要求在每个OFDM帧内其信道状态是不变的，其他环节是理想状态。

图3所表示的是两个不同的时刻状态信息，运用LCC算法是现代的比特分配，可以看出LCC算法有很好的跟踪信道状态的能力，符合设计该算法时的初衷。

图3　LCC算法的在不同信道的比特分配

图4中对比了chow算法和LCC算法此2种算法和4QAM调制使的误码率情况，从其中可以看出，在信噪比一样的情况时LCC算法比4QAM有了很大的改善，对抗信道恶劣环境的能力提高了很多；LCC算法能获得和chow算法近似的性能，但是由前面的分析可知LCC相比于chow算法显著的降低的计算复杂度。

图4　不同算法的OFDM系统误码率曲线

图5中对比了LCC算法和SBLA算法的误码率性能。在信噪比小于8之前，两者的误码率性能具有非常近似的趋势，但当达到实际通信误码率要求时(10-3～10-4)时，LCC算法仅需要更低的信噪比，从而可以看出LCC算法具有更强的抗信道恶劣环境的能力。且有表3给出的复杂度对比情况可知，LCC算法具有更低的计算复杂度，从而提高了其跟踪信道的速度。

图5　不同算法的OFDM系统误码率曲线

4结语

在本文中提出了LCC算法在误码率性能方面接近于不进行自带划分的chow算法，又因为其进行了子带的划分，显著减少了算法的迭代次数；在另一方面与固定门限的SBLA算法相比较，其计算的复杂度(反映该算法跟踪信道的能力)相近，当信噪比超过7 dB的时候，会非常显著的降低误码率。所以该算法具有非常适应的价值。当然本文对于OFDM传输系统的其他环节的技术(如同步、信道估计等)都设定为了理想状况，为了更好的在实际应用该算法，下一步的研究方向是把其它实际的情况综合进来。从而系统的研究OFDM系统。

参考文献：

[1]QI Jia-jin, CHEN Xue-ping, XIAO Sheng. Advancese of Research on Low-Voltage Power Line Carrier Communication Technology[J]. Power System Technology .2010, 34(5):161-172.

[2]AN Ning, Li Bing-bing, HUANG Min. Blind Subcarrier Modulation Classification Algorithm of Adaptive OFDM System[J]. Journal of Northwest University, 2011, 41(2): 231-234.

[3]WANG Jing-kuan, HAN Peng, XU Peng, et al. An Adaptiv Block Pilot Scheme for OFDM Systems[J]. Journal of Northeastern University,2011,32(5):642-656.

[4]HUANG Xiao-zhou, WU Si-chuan, WU Yi-yan. Novel Pilot-Free Adaptive Modulation for Wireless OFDM System[J]. IEEE Translations on Vehicular Technology. 2008: 3863-3868.

[5]TANG Chao-wei, ZHAO Li-juan, SHAO Yan-qing, et al. Adaptive Step-by-Step Power Allocation Algorithm for MIMO-OFDM Systems[J]. Journal of Huazhong University of Science and Technology, 2010.38(4):18-21.

[6]LEE S M, PARK Y S．Fast Bit and Power Allocation Algorithm for OFDM Systems[A]. IEEE VTC[C]. [S.I.]: [s.n.,] 2004:503-506.

[7]LEI Ming, ZHANG Ping. Subband Bit and Power Loading for Adaptive OFDM[A].IEEE VTC[C].[S.I.]:[s.n.],2003:1481-1486.

[8]Kobayasgu H,TENG Y Nagaosat，et al. Proposal of Grouping Adaptive Modulation Method for Burst Mode OFDM Transmission System[J]. IEICE Transactions on Communications, 2003,86(1):257-265.

[9]Grunheidr，Bolinthe，Rohline H.A Blockwise Loading Algorithm for the Adaptive Modulation Technique in OFDM Systems[A].IEEE VTC[C]. [S.I.]: [s.n.], 2001: 948-950.

[10]蔡丽萍，刘盈，薛先俊.一种吞吐量最大化的电力线OFDM分子带自适应算法[J].计算机软件与应用，2012,35(05)：1720-1723.

CAI Li-ping, LIU Ying, XUE Xian-jun. An Adaptive Algorithm with Throughput Maximization based on OFDM Sub-Bands Division for Power Line[J].Computer Applications and software, 2012, 29(6): 260-263.

[11]刘盈，代鹏飞，蔡丽萍.等.基于自带动态划分的电力线OFDM自适应算法研究[J].计算机工程与设计，2012,33(50)：260-262.

LIU Ying, DAI Peng-fei, CAI Li-ping, et al. Analysis of Adaptive OFDM Algorithm based on Dynamic Sub-Bands Division for Power Line Carrier Censor Network[J].Computer Engineering and Design,2012,33(5):1720-1724.

[12]Nansal G, Hasan Z, Hossain M J. Subcarrier and Power Adaption for Multiuser OFDM based Cognitive Radio System[A].2010 National Conference on Communications[C]. Chennai:IEEE,2010:1-5.

[13]李臣阳,高向川,张卫党.基于共轭梯度法的低复杂度信道估计[J].通信技术，2015, 48 (11): 1213-1216.

LI Chen-yang, GAO Chuan, ZHANG Wei -dang. Low Complexity Channel Estimation based on Conjugate Gradient Method[J]. Communications Technology, 2015, 48 (11): 1213-1216.

[14]Nader-Esf Ahani S, Afrasiabi M. Simple Bit Loading Algorithm for OFDM-based Systems[J]. IET Communications, 2007. 1(3): 312-316.

[15]ZHANG Shi-chao, JI Zhong-mei, CUI Wei-jia. An Efficient Subband Adaptive Bit and Power Allocation for MIMO-OFDM Systems[J]. Journal of Circuits and System, 2012, 17(4):103-110.

方四祥(1990—)，男，硕士研究生，主要研究方向为无线通信网络与传输技术。

A Novel and Low-Complexity OFDM Adaptive Modulation Algorithm

FANG Si-xiang

(College of Communications Engineering,PLA University of Science and Technology,Nanjing Jiangsu 210007,China)

Abstract：The three most classic OFDM adaptive modulation algorithms, including Hughes - Hartogs algorithm, chow algorithm and Ficher algorithm, although having the incomparable advantages in the channel utilization, requires a very large computational complexity, and this is clearly unconformable to the requirement of modern high-speed communications. With the deep research on this technology, some experts propose some division algorithms of the sub bands, such as SBLA algorithm, NUDS algorithm, IDS algorithm, these techniques although could reduce iteration complexity of the system, spend much more channel capacity resources. By using the principle of Ficher algorithm, a new sub-band division algorithm is proposed, which gives attention to both algorithm complexity and possible approximation to the channel utilization without sub-band division. Simulation results clearly verify this point.

Key words：OFDM system; sub-band division; channel capacity; adaptive modulation technique; bit error rate

作者简介：

中图分类号：TP393.03

文献标志码：A

文章编号：1002-0802(2016)01-0034-05

*收稿日期：2015-08-20；修回日期：2015-12-10Received date:2015-08-20；Revised date：2015-12-10

doi:10.3969/j.issn.1002-0802.2016.01.007