填充天然橡胶材料裂纹扩展模型的建模方法*

2016-04-13上官文斌邓建向余良渭王小莉段小成

振动、测试与诊断 2016年1期

关键词：峰值试件裂纹

上官文斌，邓建向，余良渭，王小莉，段小成，阎礁

(1.华南理工大学机械与汽车工程学院广州，510641) (2.宁波拓普集团股份有限公司宁波，315800) (3.泛亚汽车技术中心有限公司上海，201201)

填充天然橡胶材料裂纹扩展模型的建模方法*

上官文斌1,2，邓建向1，余良渭1，王小莉1，段小成1,2，阎礁3

(1.华南理工大学机械与汽车工程学院广州，510641) (2.宁波拓普集团股份有限公司宁波，315800) (3.泛亚汽车技术中心有限公司上海，201201)

填充天然橡胶材料疲劳裂纹扩模型是指裂纹扩展速率与撕裂能峰值之间的关系，它是用于橡胶减振元件疲劳寿命预测的重要模型。在裂纹扩展试验得到的填充天然橡胶材料裂纹扩展长度与循环次数的数据中，由于橡胶的应力软化现象，试验后期的部分数据不可用。为此，建立了数据处理方法，获得有效的裂纹扩展长度与循环次数数据。基于单轴拉伸载荷下填充天然橡胶材料最大应变能密度与最大应变满足幂函数关系的假设，建立了变幅加载工况下裂纹扩展长度与循环次数的数学模型和识别其模型参数的优化方法。在建立的裂纹扩展长度与循环次数模型的基础上，建立了裂纹扩展速率与撕裂能峰值关系的模型和确定模型中参数的数值方法。利用一组哑铃型试片的疲劳寿命实测数据，对建立的裂纹扩展速率模型进行了验证，证明了所建立模型的正确性。

裂纹扩展试验; 裂纹扩展长度; 循环次数; 裂纹扩展速率; 撕裂能峰值; 模型参数识别; 变幅加载工况

引言

填充天然橡胶材料由于其良好的隔振效果和缓冲性能，已经被大量应用于汽车隔振器件、车轮轮胎以及各种常用密封器件中。对填充天然橡胶材料疲劳特性的研究具有重要的理论意义和实用价值。

由断裂力学可知，材料的疲劳破坏历经裂纹的萌生、裂纹的稳定扩展、裂纹的失稳扩展以致最终造成材料断裂等演化过程。忽略臭氧、温度等环境因素的影响，只有当撕裂能峰值大于某一门槛值时，裂纹的演化才会开始[1]。当撕裂能峰值小于这一门槛值时，即便材料中有微小裂纹，裂纹也不会长大。当撕裂能峰值大于某一临界值时，裂纹会发生失稳扩展，材料瞬间发生断裂。在填充天然橡胶材料裂纹扩展特性的研究中，将这一门槛值称作为门槛撕裂能，将这一临界值称为临界撕裂能。显然，对于无限寿命设计而言，门槛撕裂能是填充天然橡胶材料重要的特性参数[1-2]。对于抗断裂设计而言，临界撕裂能是重要的特性参数。在填充天然橡胶材料疲劳裂纹扩展模型的研究[3]中，普遍认为裂纹扩展速率与撕裂能峰值满足幂函数的关系。实际上，对于填充天然橡胶材料，裂纹扩展模型满足幂法则的前提是所受载荷对应的撕裂能峰值要大于某一特定的值(不一定等于门槛撕裂能，用转折撕裂能以示区别)[3-4]。对于新配方的填充天然橡胶材料，有必要确定这一特定值的撕裂能。

笔者开展了某填充天然橡胶材料在变幅加载下的裂纹扩展试验，以建立适用于不同载荷水平下的裂纹扩展模型，其中还包括对门槛撕裂能、转折撕裂能值和临界撕裂能的确定。针对变幅载荷工况下裂纹扩展实测数据的特点，基于试验中循环载荷最大应变能密度与最大应变近似满足幂函数关系的假设，推导出此种变幅加载方式下裂纹扩展长度与循环次数的关系式及裂纹扩展长度与循环次数的扩展模型。最后，对建立的裂纹扩展模型进行了验证。

1 撕裂能与裂纹扩展速率

Thomas等[5]最早将基本的断裂力学理论应用到橡胶断裂问题,认为裂纹的扩展过程是材料释放弹性应变能用以提供裂纹扩展产生新表面所需表面能的过程，并定义裂纹扩展单位面积(A)释放出的弹性应变能(U)为橡胶的撕裂能(T)，即

(1)

其中：负号表示材料的弹性应变能随着裂纹的扩展而减少。

描述材料裂纹扩展特性的另一个重要物理量是裂纹扩展速率，定义为单位循环次数(N)下的裂纹扩展长度(a)

(2)

撕裂能比R=0(一个循环载荷周期中撕裂能的最小值Tmin和最大值Tmax之比)的载荷是橡胶材料疲劳失效中经常遇到的疲劳工况，为此笔者研究撕裂能比R=0的变幅载荷工况下的裂纹扩展特性。1965年，Lake等[3]对某填充天然橡胶进行了多个载荷幅值恒定且撕裂能比R=0的裂纹扩展试验，根据实测数据的分布特点得出受到广泛认可的裂纹扩展速率和撕裂能峰值关系的4个分段模型(如图1所示)，即

(3a)

(3b)

(3c)

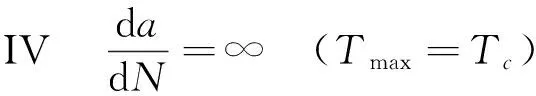
(3d)

其中：T0，Tt和Tc分别为门槛撕裂能、转折撕裂能和临界撕裂能；rz为撕裂能峰值小于T0时的裂纹扩展速率；A，B和F为材料常数。

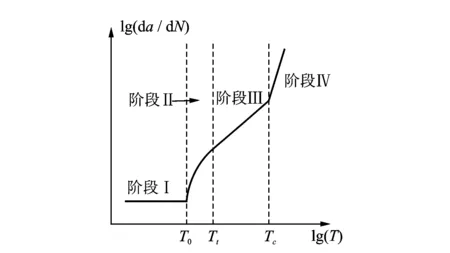
图1 填充天然橡胶材料裂纹扩展速率的4个阶段Fig.1 The four stages of filled natural rubber′s crack growth rate

在阶段I，裂纹以极小的恒定速率扩展且不受外力载荷影响[1]，门槛撕裂能T0代表了材料的抗疲劳能力。在阶段II和阶段III，裂纹扩展速率以转折撕裂能Tt为转折点由线性增长转为幂函数增长。在阶段IV，裂纹失稳扩展，裂纹扩展速率急速上升并导致材料迅速断裂。任何工况下，只要撕裂能峰值到达Tc，即可认定材料将迅速断裂，从而Tc代表了材料的抗断裂能力。

建立填充天然橡胶材料裂纹扩展模型关键在于获取裂纹扩展速率。对于撕裂能比R=0的恒幅载荷裂纹扩展试验，试件的撕裂能峰值保持不变，裂纹扩展速率为恒定值，则裂纹扩展长度与循环次数成正比例关系。但是在变幅载荷加载工况，试件的撕裂能峰值不断变化，裂纹扩展速率不再是恒定值，其裂纹扩展长度与循环次数的关系还有待研究。

2 裂纹扩展长度模型与裂纹扩展模型的建立方法

裂纹扩展长度模型是裂纹扩展长度与循环次数之间的关系。裂纹扩展模型是裂纹扩展速率与撕裂能峰值之间的关系。基于单轴拉伸载荷下最大应变能密度与最大应变满足幂函数关系的假设，笔者建立裂纹扩展长度数学模型，根据试验给出的实测数据，先后建立求解裂纹扩展长度模型与裂纹扩展模型中模型参数的最优化方法。

2.1 裂纹扩展长度与循环次数关系的模型

2.1.1 裂纹扩展长度与循环次数关系的理论模型

实际设计的裂纹扩展试验中，所施加载荷对应的撕裂能峰值在T0～Tc之间变化，即载荷水平在阶段II和阶段III之间。因此，实际试验中填充天然橡胶材料裂纹扩展速率与撕裂能峰值的关系可近似由式(3b,3c)表示，改写为

(4)

其中：D=AT0-rz；A，D，B和F为待确定的材料常数。

纯剪试件的撕裂能与裂纹尺寸无关，通常采用纯剪试件进行裂纹扩展试验。试验中纯剪试件的撕裂能峰值计算公式[3]为

(5)

其中：h为试件标距；Wmax为试件上远离裂纹尖端处的应变能密度峰值，由试件在当前载荷循环卸载段的应力应变曲线积分所得[6]。

在单轴拉伸载荷下中填充天然橡胶材料的最大应变能密度(Wmax)与最大应变(εmax)近似满足幂函数关系[6-8]，即

(6)

其中：k和b为待确定常数。

在变幅工况下加载的最大应变载荷幅值(εmax)与循环次数(N)满足线性增长的关系，则

(7)

其中：c和d为已知常数。

根据式(5)～(7)，试验过程的撕裂能峰值(Tmax)可用循环次数(N)表示为

(8)

将式(8)代入式(4)，可得裂纹扩展速率与循环次数的关系式为

(9)

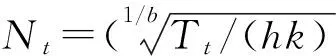
裂纹扩展长度表示为Δa=a-a0，其中，a0为纯剪试件的初始裂纹长度。对式(9)进行不定积分，可得试验过程中裂纹扩展长度(Δa)与循环次数(N)的关系为

(10)

其中：E和H为待确定常数。

由式(10)可知，对于撕裂能比R=0的裂纹扩展试验，若单轴拉伸(非平面拉伸或者双轴拉伸)试验施加的应变载荷幅值随循环次数线性增加，则裂纹扩展长度(Δa)与循环次数(N)存在确定的函数关系。

式(10)中，常数k，b可通过式(6)对试验所得到的循环载荷最大应变能密度与最大应变进行幂函数拟合获取。在此基础上，通过优化算法可确定式(10)中的其他常数A，B，D，E，F和H，但此种方法会将常数k，b的误差引入到式(10)中。为了避免常数k，b引入的误差，可先将式(10)改写为

(11)

其中：Af，Df，Ef，Bf，Hf，p，q和Nt均为待确定参数，但是这些参数之间并不是独立的。

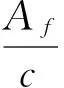
(12)

对式(11)关于循环次数N求导，可得裂纹扩展速率与循环次数的关系式为

(13)

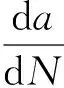
(14)

结合式(11)、式(13)和式(14)，整理可得

(15)

2.1.2 裂纹扩展长度理论模型参数的确定方法

由式(12)与式(15)可知，待确定常数Ef，Bf和Hf可由Af，Df，p，q和Nt等5个待确定参数表示。因此，只需获取Af，Df，p，q和Nt等5个待确定常数，即可确定裂纹扩展长度与循环次数的关系式(11)。

为了能从实测裂纹扩展长度和循环次数数据中确定常数Af，Df，p，q和Nt，根据式(11～15)，建立最优化模型

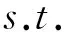
其中：目标函数f为裂纹扩展长度实测值(Δa)和计算值(Δacal)的偏差平方和；n为裂纹长度实测有效数据总数；Ni为第i个循环次数；Δai为循环次数Ni对应的裂纹扩展长度实测值；Δacal,i为循环次数Ni对应的裂纹扩展长度拟合值；其他参数的意义参考式(11)～(15)。

2.2 裂纹扩展速率与撕裂能峰值关系的模型

求解式(16)最优化问题，可得到裂纹扩展速率与循环次数关系式(13)中的各个待确定常数，从而得到试件不同实测循环次数时的裂纹扩展速率。填充天然橡胶试件的撕裂能峰值可以通过计算的方法得到[4]，由此得到试件裂纹扩展速率和撕裂能峰值的关系。利用式(4)描述的裂纹扩展速率与撕裂能峰值关系理论模型，建立最优化方法来确定模型中的各个材料参数。

纯剪试件的裂纹扩展试验一般要在一批相同材料试件上进行多次重复试验，从而减少偶然或其因素引起的试验误差。对于同一批填充天然橡胶材料试件，无论试件形式、试验条件和加载工况等因素，试件裂纹扩展模型(如式(4)所示)中的待确定常数数值均一样。因此，应将所有的同一批试件的裂纹扩展速率和撕裂能峰值数据视为一个整体，作为获取裂纹扩展模型的原始数据。

式(4)中，由于rz很小，处理试验数据时一般认为rz=0，则有D=AT0。因此，式(4)可变形为

(17)

其中：裂纹扩展速率为[T0，Tc]上的连续函数。

(18)

所有试件实测数据整合后的撕裂能峰值序列记为Tmax,1，Tmax,2，Tmax,3…Tmax,i…Tmax,n，对应的裂纹扩展速率原始值序列记为r1,r2,…,ri,…,rn，其中，n为整合后的数据总数。为确定式(17)中的待确定常数B，F，T0和Tt，建立以下最优化模型来求解。

(19)

其中：目标函数f为裂纹扩展速率原始值与拟合值的偏差平方和；rcal,i为对应撕裂能峰值Tmax,i的裂纹扩展速率拟合值；其他参数的意义参考式(4)。

3 裂纹扩展长度模型与裂纹扩展模型建立方法的应用

为了验证填充天然橡胶材料疲劳裂纹扩展模型建立方法的正确性，对某填充天然橡胶材料的纯剪试件进行变幅加载裂纹扩展试验。在得到有效的裂纹扩展长度、撕裂能峰值与循环次数实测数据后，根据建模方法建立所研究填充天然橡胶材料的疲劳裂纹扩展模型。

3.1 变幅加载时裂纹扩展试验实测数据分析

裂纹扩展试验的主要目的是获取材料的裂纹扩展特性，即裂纹扩展速率与撕裂能峰值的关系。试验通过测量试件的裂纹长度值并记录对应的循环次数来获取裂纹扩展速率，结合实测的撕裂能峰值数据，用数学方法建立裂纹扩展模型。

已知本裂纹扩展试验所采用纯剪试件的断裂应变为188.53%，临界撕裂能为174 007.8 J/m2。为了快捷地得到不同载荷水平下的裂纹扩展数据，笔者采用撕裂能比R=0的线性变幅加载工况。

试验采用3个纯剪试件(sp1，sp2和sp3)进行3次重复试验，其中，试件的初始裂纹a0=25 mm。如图2所示，试验施加的应变载荷谷值一直保持为零，而峰值随循环次数线性增加。根据试验设定，式(7)中的待确定常数c=2.500 6×10-6，d=0.029 7。

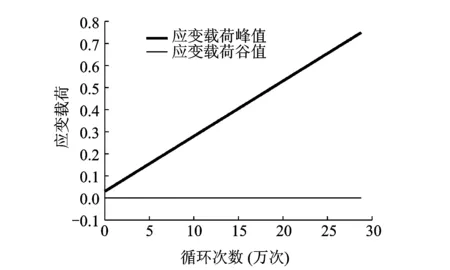
图2 变幅加载裂纹扩展试验中应变载荷随循环次数的变化Fig.2 The relationship between strain and number of cycles in crack growth experiment under variable amplitude

试验实测裂纹长度与撕裂能峰值数据如图3所示。由于应力软化和永久变形等缘故[8]，随着循环次数的增加，试验加载的最大应力载荷不断减小，导致载荷循环最大应变能密度的增长速度下降甚至减小。图3(b)中，受应力软化和永久变形的影响，在循环次数约大于20万次后，撕裂能峰值的增长速度开始减小，撕裂能峰值甚至下降，与式(8)中撕裂能峰值的变化规律不符。为获得建立裂纹扩展模型的有效试验数据，应剔除试验后期受应力软化和永久变形影响的实测数据。

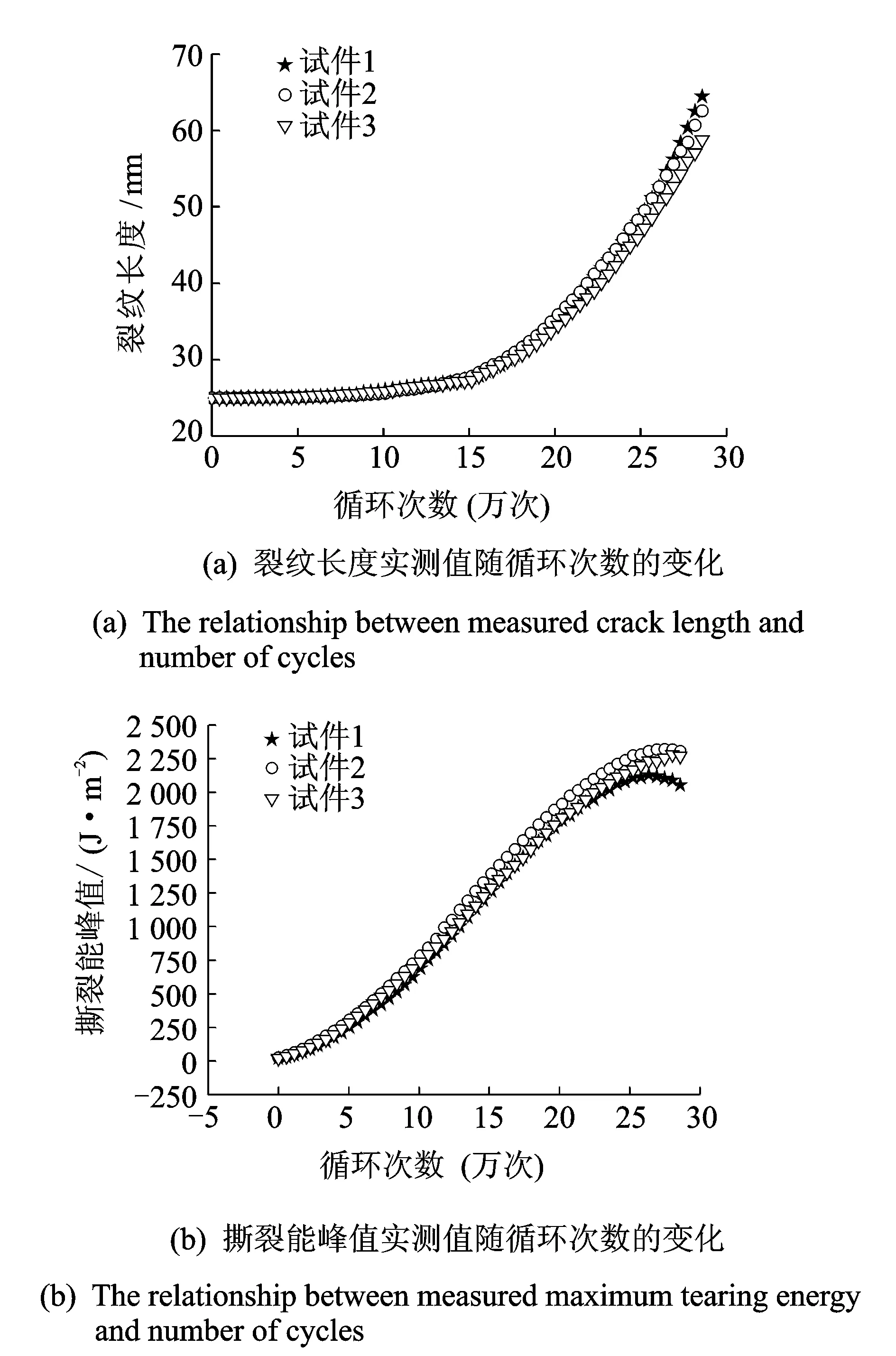
图3 变幅加载工况下实测裂纹长度与撕裂能峰值的变化Fig.3 The measured value of crack length and maximum tearing energy

图4 循环载荷最大应变能密度与最大应变的关系Fig.4 The relation of maximum strain energy density and maximum strain

3.2 裂纹扩展试验有效实测数据的选取

如图4所示，在试验前期，循环载荷最大应变能密度与最大应变实测数据在双对数坐标系下基本成线性分布，与式(6)的幂函数关系相符。在试验后期，由于最大应变能密度的下降，导致试验数据不再是线性分布。为准确剔除不再按照线性分布的实测数据，笔者采用最小二乘法对最大应变能密度与最大应变进行线性拟合，并依据相关系数的大小对实测数据进行截断。

在式(6)两边取常用对数，得最大应变能密度与最大应变的线性拟合模型

(20)

设试件最大应变能密度实测数据的总数为n，在第m(m≤n)个数据点对最大应变能密度与最大应变进行截断，取第m个数据点后面的所有最大应变能密度与最大应变数据进行线性拟合。各试件试验数据的拟合相关系数R随截断点m的变化曲线如图4所示。

两个变量线性拟合的相关系数越接近1，则两个变量的线性相关性越强。令数据截断位置的相关系数为0.95，当最大应变能密度与最大应变线性拟合的相关系数小于0.95时，认为此时应力软化和永久变形等现象已经对试验数据产生影响。如图5所示，3个试件的数据总数均为1 028，用相关系数R=0.95去截断数据，可得数据截断点的m值分别为607，759和889。其中，3个数据截断点对应的循环次数分别为169 963，212 523和248 923。

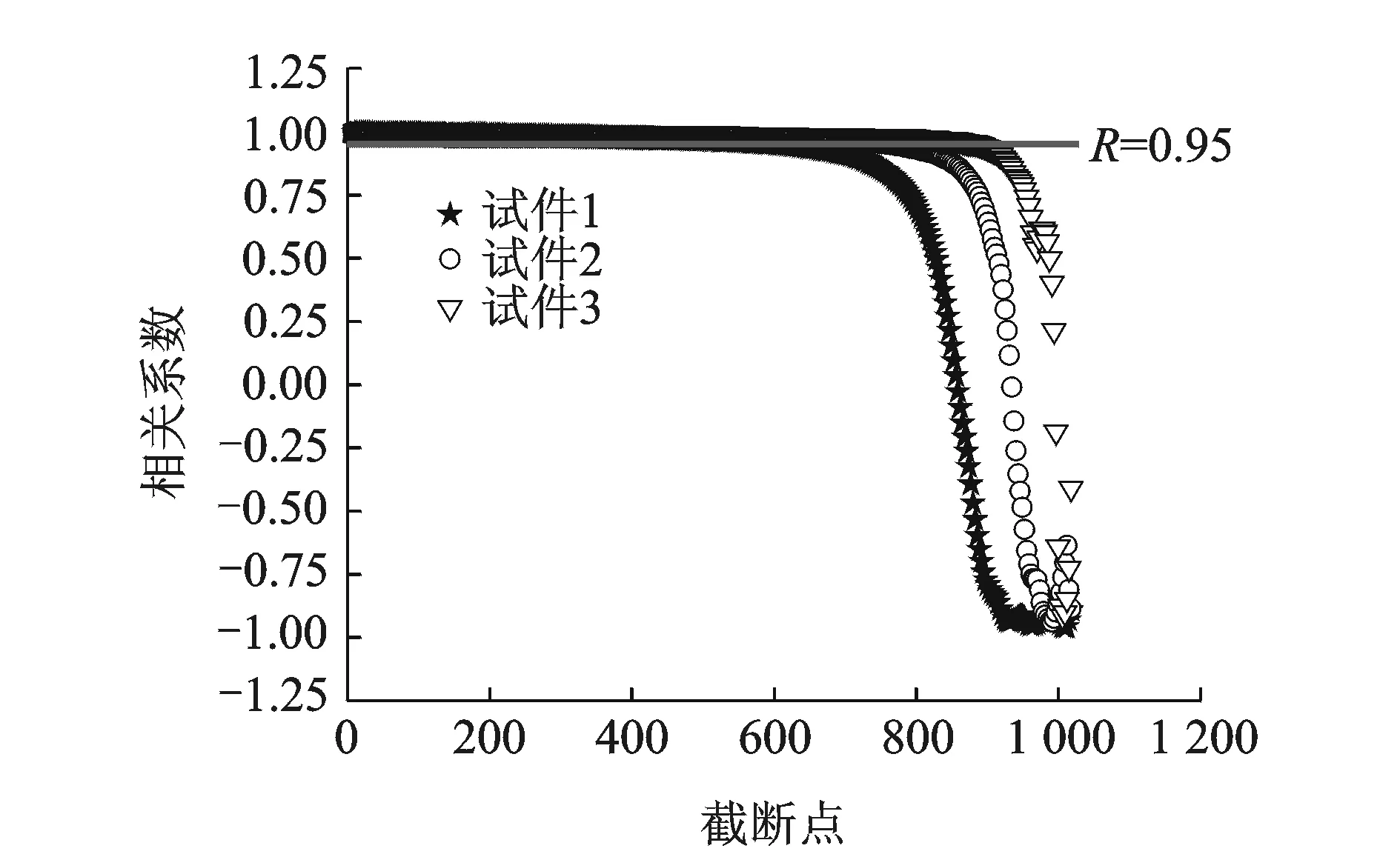
图5 截断点m对拟合相关系数R的影响Fig.5 The influences of cut-off points on fitting correlation coefficient

3.3 裂纹扩展模型中材料参数的确定

3.3.1 裂纹扩展长度与循环次数模型参数的确定

根据得到的裂纹扩展长度与循环次数有效实测数据，求解式(16)的最优化问题。记实测循环次数序列为N1，N2，N3，…，Ni，…，Nn。求解时，假设转折循环次数Nt为实测循环次数中的某一具体值Ni，从而可将实测数据划分为两部分。根据式(11)中两个阶段的关系式，分别对两部分裂纹扩展长度与循环次数实测数据进行最小二乘拟合。两个最小二乘拟合偏差平方和的加和，即为式(16)最优化问题的目标函数值，记为fi。当转折循环次数Nt取遍实测循环次数序列时，对应可得目标函数值序列，记为f1，f2，f3，…，fi，…，fn。目标函数值序列最小值对应的最小二乘拟合结果即为最优化问题的最优解。对应最优解，3个试件裂纹扩展长度与循环次数关系式中各待确定参数拟合结果如表1所示。

图6为各个试件裂纹扩展长度与循环次数实测值和拟合值的对比，由图可知实测数据和拟合曲线吻合较好。将表1各个材料常数的值代入式(13)，可得各试件试验过程中裂纹扩展速率的变化情况，结果如图7所示。当循环次数约大于10万次之后，各个试件的裂纹扩展速率增长均明显加快。

表1 3个纯剪试件裂纹长度和循环次数关系式中各个待确定常数的拟合结果

Tab.1 The fitting results of variables in the equations between crack length and number of cycles for the three pure shear test pieces

试件AfDfpEfBfqHfNt16.52×10-51.95×10-62.4657-0.004534.23×10-44.90000.722212460324.14×10-54.07×10-132.6301-0.001625.59×10-44.86000.16968260332.94×10-51.99×10-162.2107-0.005003.58×10-44.42470.237482603

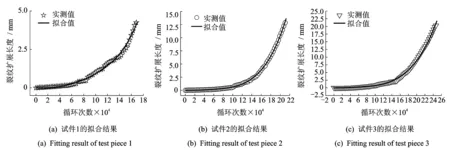
图6 裂纹扩展长度实测值与拟合值的对比Fig.6 The comparison of measured and fitted values of crack growth length

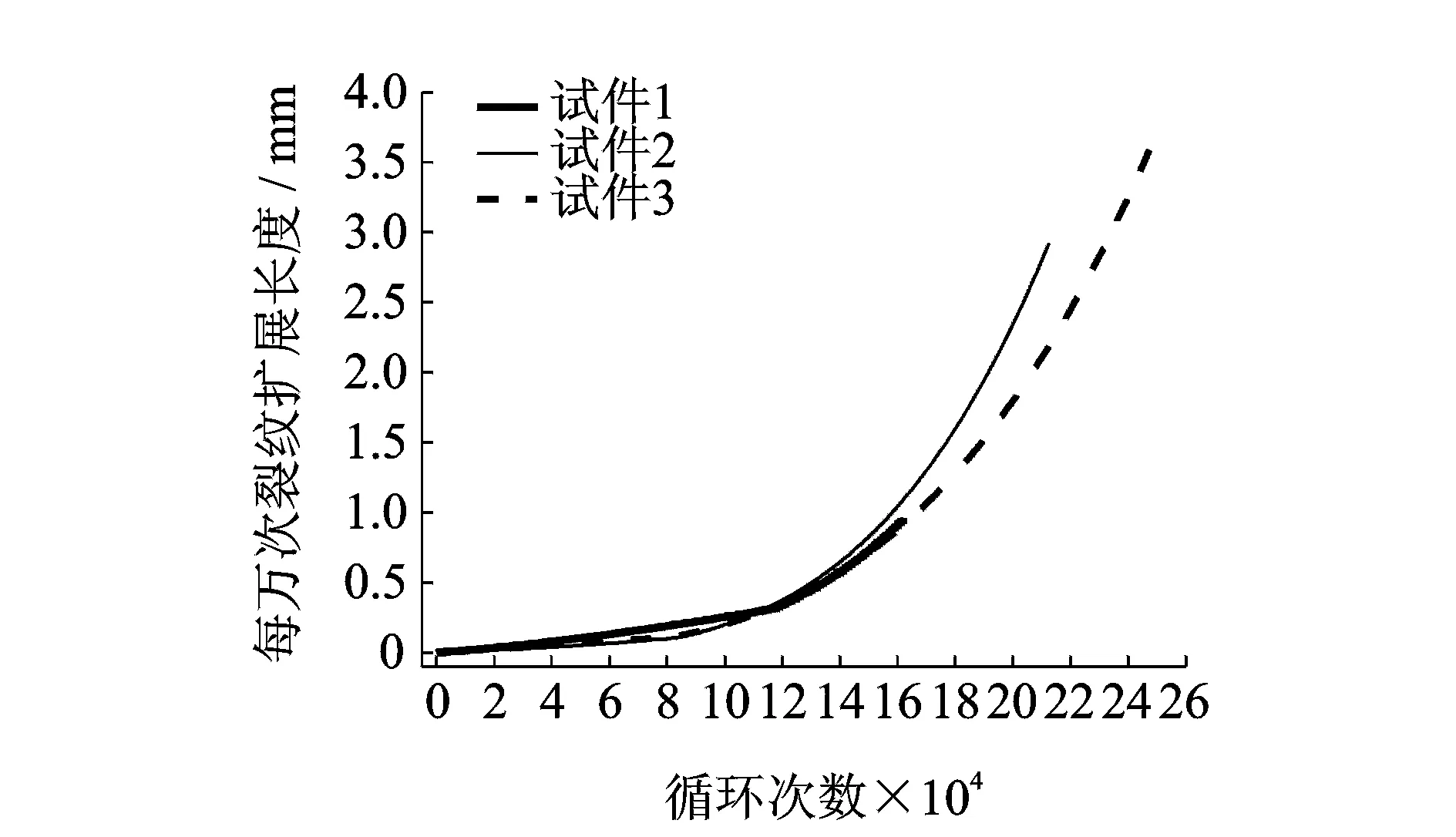
图7 裂纹扩展速率随循环次数变化的拟合曲线Fig.7 The fitted curve between the crack growth rate and number of cycles

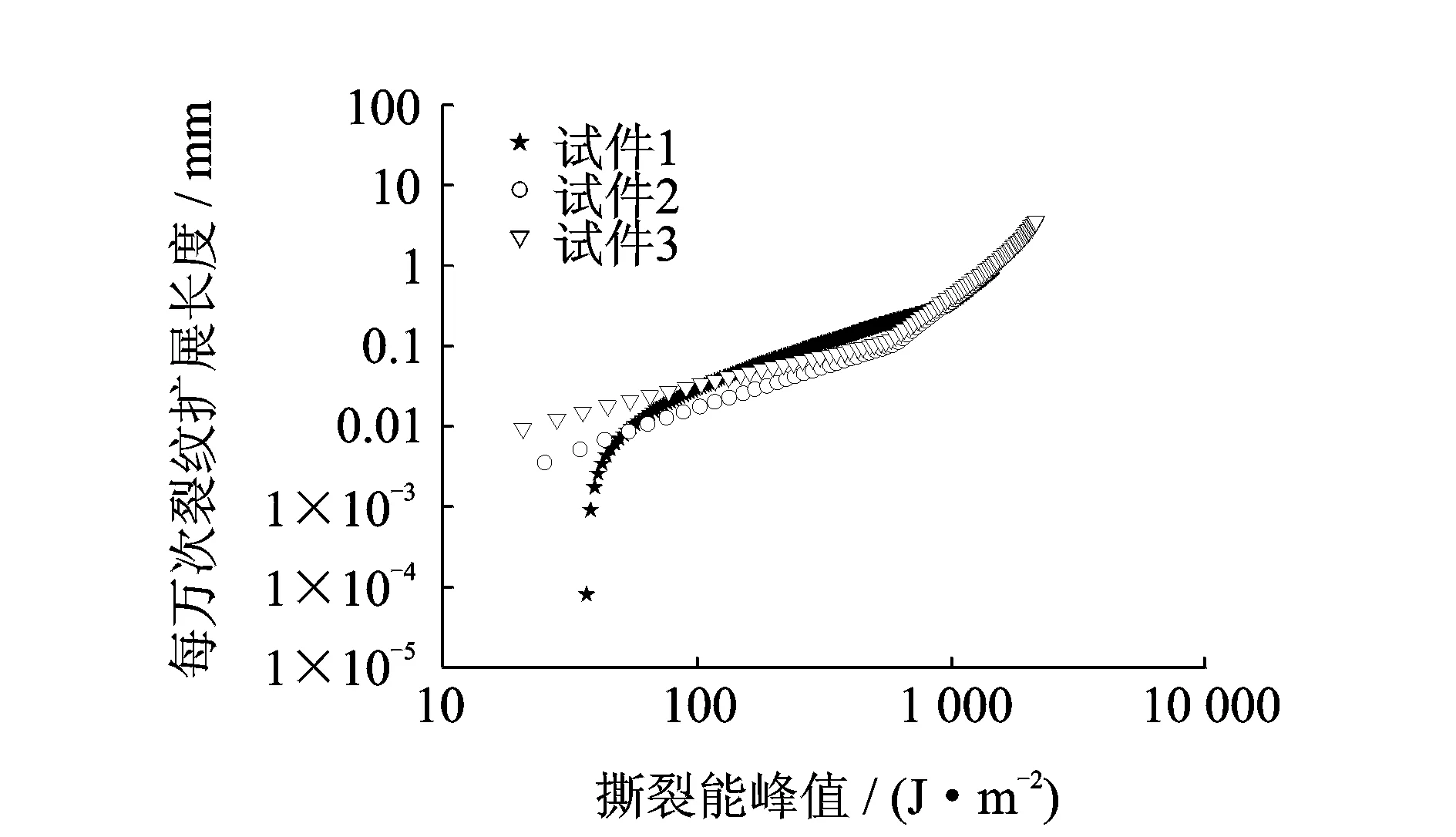
图8 裂纹扩展速率拟合值与撕裂能峰值实测值的变化关系Fig.8 The relation between fitted values of crack growth rate and measured values of maximum tearing energy

3.3.2 裂纹扩展速率与撕裂能峰值模型参数的确定

图8为各试件的裂纹扩展速率和撕裂能峰值实测数据。在撕裂能峰值约小于500 J/m2前，裂纹扩展速率增长缓慢，试件每万次裂纹扩展长度增长的平均速度约为2.5×10-4mm/(J·m-2)；而在撕裂能峰值约大于800 J/m2后，裂纹扩展速率快速增长，试件每万次裂纹扩展速率增长的平均速度约为1×10-3mm/(J·m-2)。裂纹扩展速率随撕裂能峰值的增长模式明显存在两个不同规律，与式(4)描述的理论模型相符，因此可通过求解式(19)的最优化问题来建立所研究填充天然橡胶材料的裂纹扩展模型。

基于3个试件裂纹扩展速率和撕裂能峰值整合后的数据，求解式(19)的最优化问题。当转折撕裂能Tt取遍所有实测撕裂能峰值序列Tmax,1，Tmax,2，Tmax,3，…，Tmax,i，…，Tmax,n时，对应可得目标函数值序列。目标函数序列的最小值对应的模型参数用来描述裂纹扩展速率与撕裂能峰值的模型参数。当目标函数取最小值时，求解得到的撕裂能门槛值T0、转折撕裂能Tt与材料常数A,B,F如表2所示。

表2 填充天然橡胶材料裂纹扩展模型中各个待确定常数的拟合结果

Tab.2 The fitting results of all variables in crack growth model

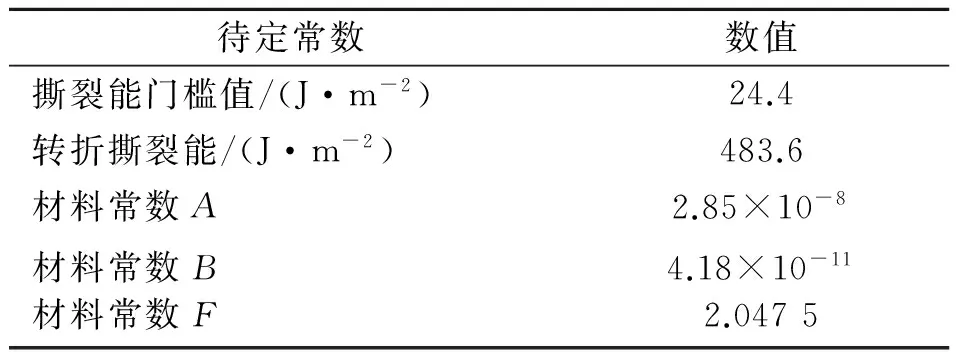
待定常数数值撕裂能门槛值/(J·m-2)24.4转折撕裂能/(J·m-2)483.6材料常数A2.85×10-8材料常数B材料常数F4.18×10-112.0475

如图9所示，裂纹扩展速率与撕裂能峰值的原始数据和拟合的关系曲线吻合良好。将表2中的数据代入式(17)，结合式(3)，可得笔者研究填充天然橡胶材料的裂纹扩展模型为

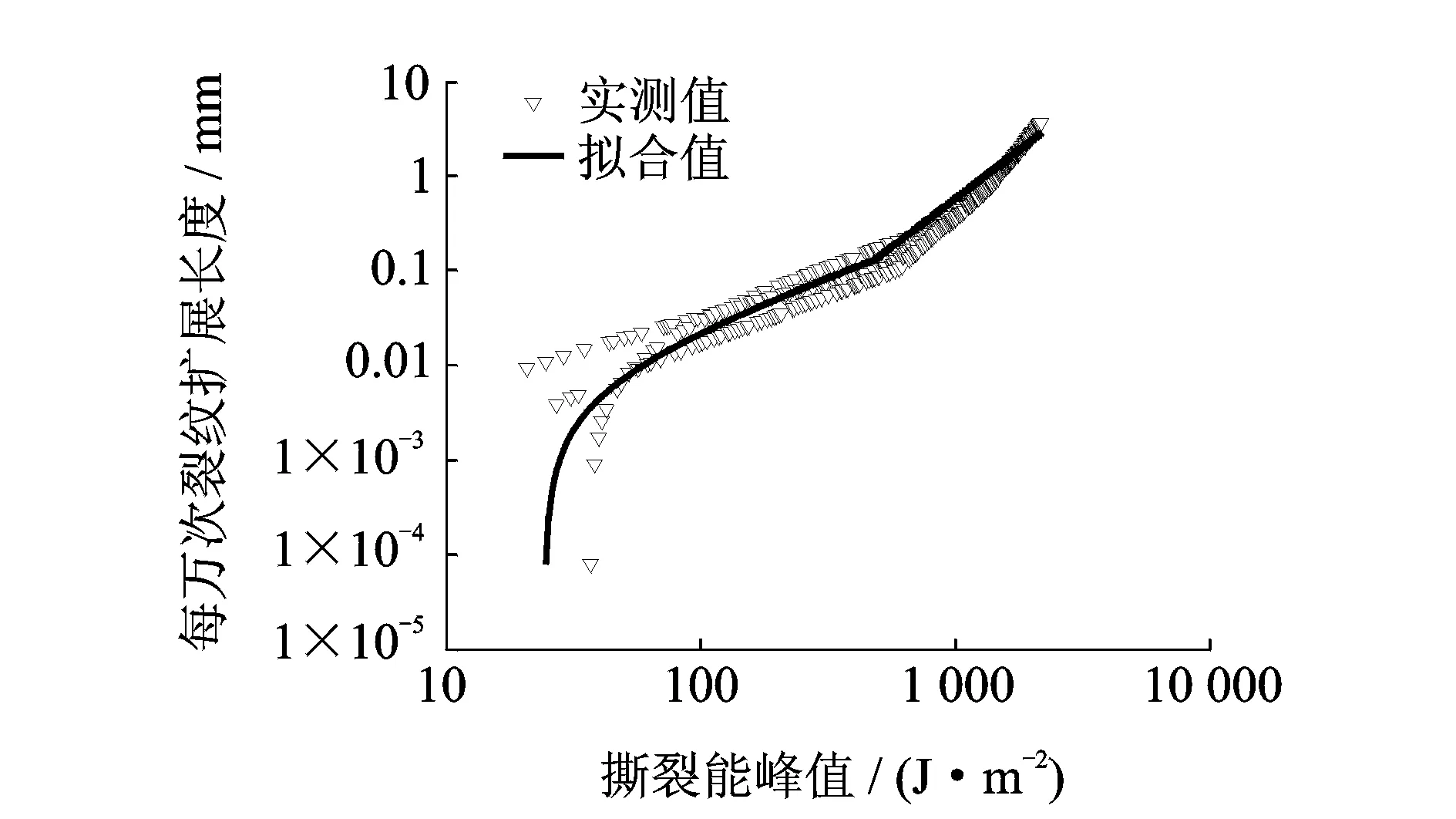
图9 裂纹扩展速率与撕裂能峰值的关系曲线Fig.9 The relation curve of crack growth rate and maximum tearing energy

(21)

4 裂纹扩展模型的验证

为了验证式(21)中裂纹扩展模型的正确性，笔者试制同配方的哑铃型试片进行单轴拉伸疲劳试验[7]，获取试片在不同恒幅载荷水平下的疲劳寿命。

哑铃型试片的单轴拉伸疲劳试验过程参见文献[7]。笔者一共开展了8个不同应变峰值的恒幅载荷疲劳试验，每一工况下分别对20个填充天然橡胶哑铃型试片进行重复试验，将各个工况的20个实测寿命取平均值，如表3所示。

表3 哑铃型试片疲劳试验应变和实测寿命

Tab.3 The strain and measured lifetime of all dumbbell-shaped test pieces

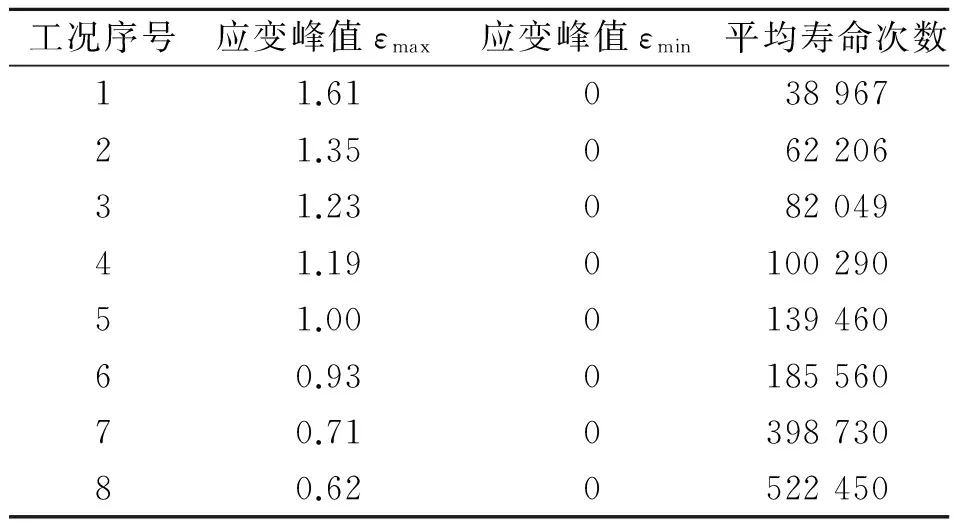
工况序号应变峰值εmax应变峰值εmin平均寿命次数11.6103896721.3506220631.2308204941.19010029051.00013946060.93018556070.71039873080.620522450

在实际试验中，不论撕裂能峰值处于图1中的哪一阶段，阶段III的裂纹扩展特性可近似代替其他几个阶段的扩展行为[9]。因此，计算疲劳寿命时可认为裂纹扩展速率与撕裂能峰值成幂函数关系。文献[9]给出了哑铃型试片单轴拉伸疲劳试验的寿命预测公式

(22)

其中：Np为试件的疲劳寿命预测值；a0为试片橡胶材料的初始裂纹长度；B，F为式(17)中的材料常数；k为一个与材料类型和远离裂纹尖端的应变水平相关的系数[4]；W为试片远场的应变能密度。

将式(22)中的疲劳寿命预测值Np用实测值Nf代替，则式(22)可变形为橡胶材料初始裂纹的计算式

(23)

随机选择工况1，2，4，7的实测疲劳寿命代入式(23)计算材料的初始裂纹。其中，Nf取表3中各工况的实测疲劳寿命值。各工况下材料的初始裂纹与平均初始裂纹如表4所示。各个初始裂纹值较为接近，可取其平均值0.023 2 mm作为笔者所采用填充天然橡胶材料的初始裂纹a0。填充天然橡胶材料的初始裂纹一般分布在0.02～0.06 mm之间[10]，因此本研究初始裂纹的计算结果较为合理。

表4 工况试片平均寿命及其对应的初始裂纹

Tab.4 The average lifetimes and initial crack lengths of selected operating conditions

工况序号应变峰值εmax实测平均寿命次数初始裂纹/mm平均值a0/mm11.61389670.026021.35622060.02500.023241.191002900.021370.713987300.0203

如表5所示，将初始裂纹平均值a0代入式(22)计算哑铃型试片在剩余工况3，5，6，8中的预测疲劳寿命，并将其结果与实测疲劳寿命进行对比。各工况预测寿命与实测寿命的比值分布在[0.93,1.03]之内，说明预测寿命和实测寿命有较好的一致性。

表5 哑铃型试片预测疲劳寿命与实测疲劳寿命的对比

Tab.5 The comparison of predicted and measured values of dumbbell-shaped test pieces′ lifetime

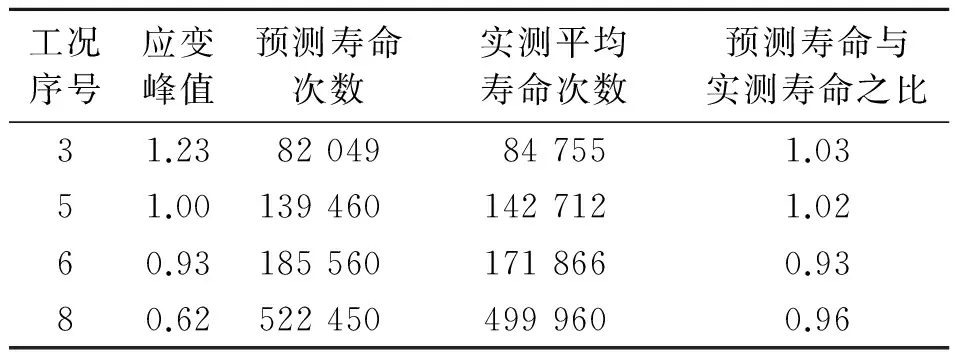
工况序号应变峰值预测寿命次数实测平均寿命次数预测寿命与实测寿命之比31.2382049847551.0351.001394601427121.0260.931855601718660.9380.625224504999600.96

可见，无论是根据实测寿命计算初始裂纹，还是根据初始裂纹计算预测寿命，式(21)的裂纹扩展模型均能给出较好的计算结果，验证了所建立裂纹扩展模型的正确性和获取裂纹扩展模型方法的正确性。

5 结论

1) 建立了变幅载荷单轴拉伸试验中获取有效裂纹扩展长度与循环次数实测数据的数据处理方法，剔除试验后期受到橡胶的应力软化现象影响的实测数据。

2) 给出了单轴拉伸试验下裂纹扩展长度与循环次数模型的建模方法。利用实测的有效裂纹扩展长度与循环次数的试验数据和建立的裂纹扩展长度理论模型，提出了求解模型中材料参数的最优化方法。

3) 建立了填充天然橡胶材料裂纹扩展模型中材料参数的数值求解方法，得到了填充天然橡胶材料的门槛撕裂能、转折撕裂能和临界撕裂能等重要的材料参数。用一组哑铃型试片单轴拉伸疲劳试验的结果验证了该模型的正确性。

[1] Lake g J,Lindley P B. The mechanical fatigue limit for rubber[J]. Journal of Applied Polymer Science, 1965, 1233-1251.

[2] Lake G J,Lindley P B.Fatigue of rubber at low strains[J]. Journal of Applied Polymer Science, 1966, 343-351.

[3] Gent A N， Lindley P B, Thomas A G. Cut growth and fatigue of rubbers I the relationship between cut growth and fatigue [J]. Journal of Applied Polymer Science, 1964, 8: 455-466.

[4] Lindley P B. Relation between hysteresis and the dynamic crack growth resistance of natural rubber [J]. International Journal of Fracture, 1973(9):449-462.

[5] Thomas A G. Rupture of rubber V cut growth in natural rubber vulcanizates [J]. Journal of Polymer Science, 1958, 31: 467-480.

[6] Mars W V. Multiaxial fatigue of rubber [D]. USA: The University of Toledo, 2001.

[7] 王小莉，上官文斌，刘泰凯，等. 填充橡胶材料单轴拉伸疲劳试验及疲劳寿命模型研究[J]. 机械工程学报，2013，49(14)：65-73.

Wang Xiaoli, Shangguan Wenbin, Liu Taikai, et al. Experiment of uniaxial tension fatigue and modeling of fatigue life for filled natural rubbers [J]. Journal of Mechanical Engineering, 2013, 49(14)：65-73.(in Chinese)

[8] Mars W V, Fatemi A. Factors that affect the fatigue life of rubber: a literature survey[J]. Rubber Chemistry and Technology, 2004,76:391-412.

[9] Lake G J. Fatigue and fracture of elstomers [J]. Rubber Chemistry and Technology,1995,68(3): 435-459.

[10]Mars W V, Fatemi A. A literature survey on fatigue analysis approaches for rubber [J]. International Journal of Fatigue, 2002, 24: 949-961.