地球静止轨道远程交会过程导航性能评估

任家栋，曾庆双，朱 虹

（1. 哈尔滨工业大学 航天学院，哈尔滨 150001；2. 上海航天控制技术研究所，上海 201109；3. 上海市空间智能重点实验室，上海 201109）

地球静止轨道远程交会过程导航性能评估

任家栋1,2,3，曾庆双1，朱 虹2,3

（1. 哈尔滨工业大学 航天学院，哈尔滨 150001；2. 上海航天控制技术研究所，上海 201109；3. 上海市空间智能重点实验室，上海 201109）

远程交会是静止轨道共位卫星自主定点置入的关键途径。针对远程交会过程中大距离跨度下相对运动模型的误差信号特性，理论推导了误差的传递机理，给出了相对导航EKF算法期望及噪声特性的定量分析模型。研究表明，确定距离区间存在最优过程噪声量级及其对应的最优滤波性能，且滤波误差与交会距离正相关，可作为全局最优滤波器的定量设计依据，解决了静止轨道远程交会过程EKF导航算法性能的量化评估问题。仿真表明，分析结论正确，相对速度滤波误差全程优于0.005 m/s (1σ)，满足交会任务需求。

地球静止轨道卫星；自主；远程交会；相对导航；滤波精度

远程交会是指追踪星在测量数据的支持下，通过大幅度、远距离的机动变轨，进入到目标星附近的某特定区域。远程交会往往是在轨服务和空间作战等任务中能量消耗最大、时间消耗最长的阶段。对于地球静止轨道（GEO）卫星，轨道的稀缺特性致使多星共位已成为国际上共享轨道资源的主要措施。卫星利用自身的雷达等进行远程自主交会，建立稳定的多星共位关系，可有效提高定点置入效率，是当前应用研究的热点之一。

相对导航是自主交会的基础。近年来国内外研究成果较多[1-3]，导航方案多采用基于 CW（Clohessy-Wiltshire）方程的EKF（Extented Kalman Filter）相对导航算法。在远程交会过程中，距离跨度较大（10～100 km），CW 方程的未建模误差是有色信号且随距离变化。文献[4]采用 H∞滤波器抑制建模误差，此时滤波系统退化为次优状态；文献[5]利用误差分析理论研究了在初始条件、误差噪声模型部分或全部不精确已知的情况下最优等价滤波器的设计方法，但该方法并不适应于有色噪声。同时EKF相对导航算法由于观测方程非线性导致直接应用滤波误差分析理论存在困难[6]，因此滤波系统真实性能的量化分析研究较少，目前多依赖事后数据评估[7]。理论分析表明，无迹转换（Unscented Transformation）等可以实现信号均值及其高阶矩的高精度非线性转换[8]。文献[9]对于加性噪声的UKF系统进行了性能评估，文献[10-11]对于导航系统量测噪声的误差传递特性进行了分析。本文基于同样的思路，采用非线性转化建立基于间接测量的相对导航系统，推导滤波误差的传递机理，根据CW方程在静止轨道的误差特点，定量研究自主相对导航EKF算法的滤波精度，理论上解决了静止轨道远程交会过程中导航性能的评估问题。

1 静止轨道相对运动方程误差分析

远程交会中实施控制的卫星称为追踪星，目标区域的定点卫星称为目标星。

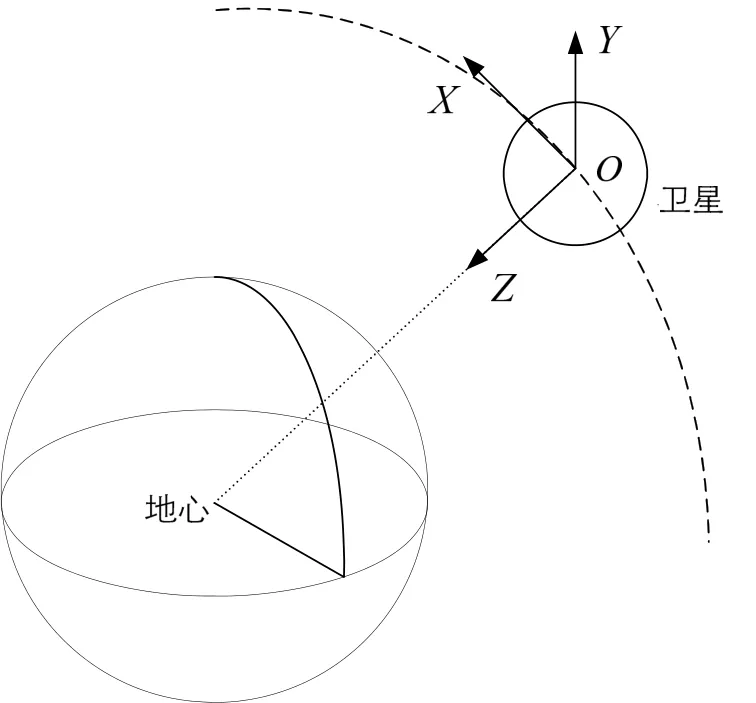
图1 相对运动坐标系Fig.1 Relative motion coordinate system

在近圆轨道下，考虑轨道环境摄动，两星相对运动动力学方程为

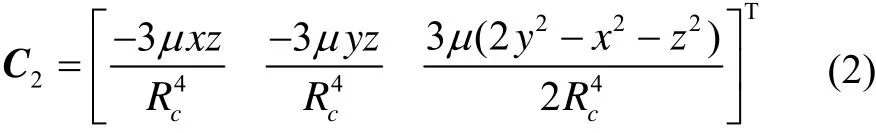
式中：μ为地球引力常数，Rc表示地球静止轨道星地距离。

地球静止轨道卫星星地距离为42 164 km，两星共位保持距离ρ=20 km，此时，

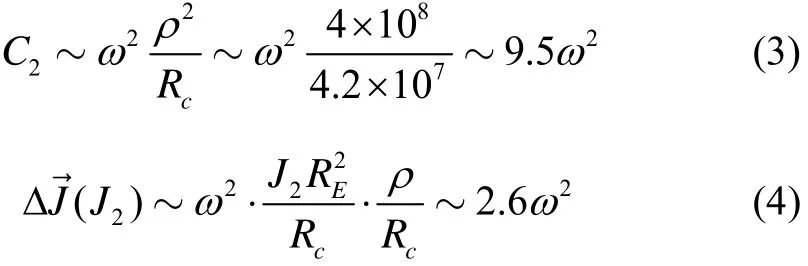
比较以上两式，从量级上可见，中心引力二次项C2约为由J2项引起的相对摄动加速度的4倍。因此，对于远程交会，CW 方程的主要误差源是中心引力二次项，并且误差幅值与交会距离的平方成正比。

结合CW方程的解析解，分析式(2)可得，CW方程的未建误差是有色信号，各轴误差均含有周期振荡信号，振荡周期为1/2轨道周期，同时Z轴误差还包含常值漂移项。

2 间接量测相对导航设计

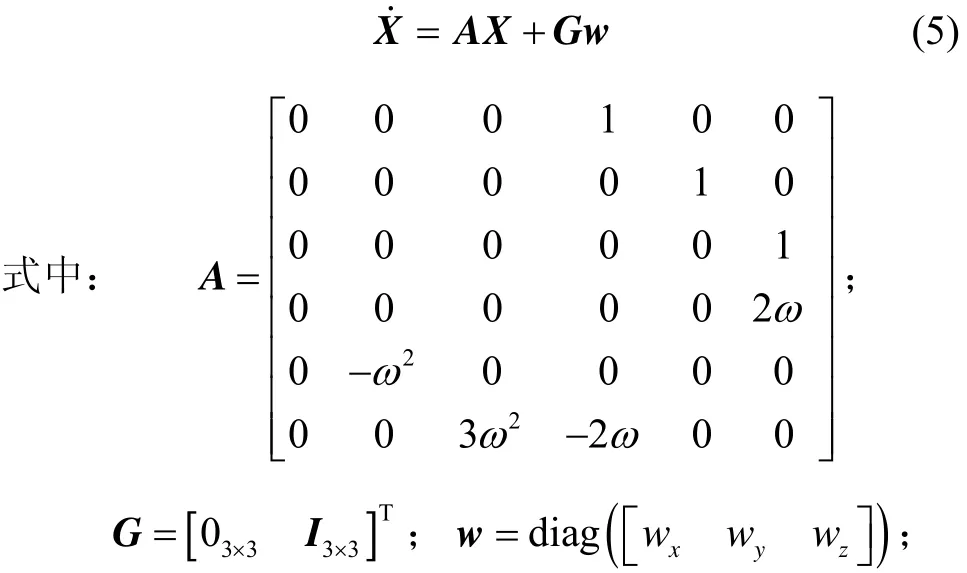
采样时间T，对式(5)离散得：

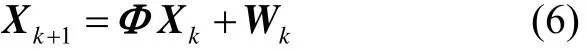
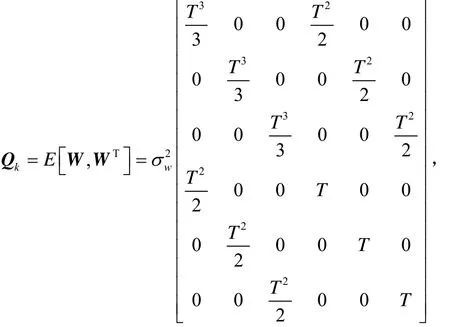
雷达量测方程为

式中：ρ为两星的视线距，ψ为雷达测量航向角，θ为雷达测量俯仰角，V为雷达测量噪声。

将雷达测量坐标系下的测量值采用一阶近似转化到轨道坐标系下，形成间接测量方程。采用 Monte Carlo分析可知，精度与无迹转换相当[8]。

转换关系如下：

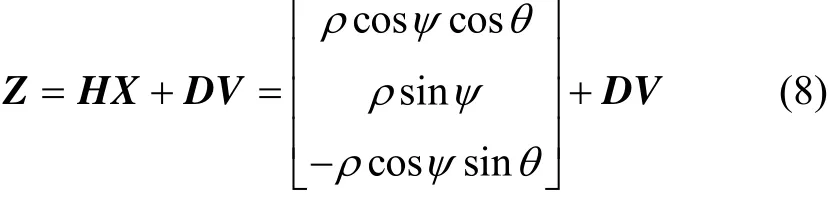
式中：

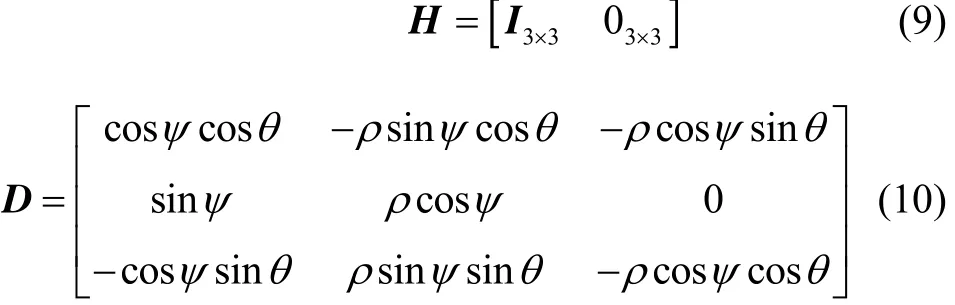
转化后方差：

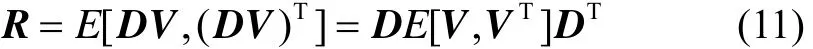
通常远程交会过程相对指向角度较小，雅可比矩阵明显对角占优且变化较小，可近似取

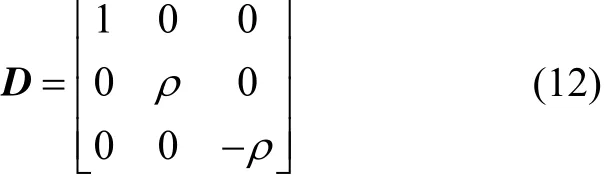
根据某实际系统取雷达噪声，测距误差0.0005ρm(1σ)，测角误差0.1°(1σ)。此时，式(6)和式(8)组成了基于标准卡尔曼滤波器的相对导航系统。

3 相对导航滤波性能分析

滤波精度是滤波器性能的主要指标。状态方程存在未建模误差的情况下，滤波估计方差不能反映滤波状态的真实方差。

CW 方程在静止轨道的未建模误差特性以常值偏差和1/2轨道周期振荡为主。振荡周期远低于滤波系统等效带宽，对滤波系统整体性能影响较小，主要考虑CW方程的未建模误差中的常值信号。

卡尔曼滤波器如(6)(8)，其基本递推方程为

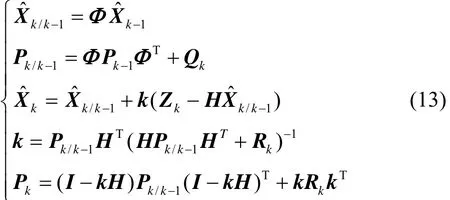
式中：Qk、Rk分别为系统过程噪声阵和量测噪声阵，P为系统状态方差阵，k为滤波增益阵。

理论模型下滤波估计方差满足：

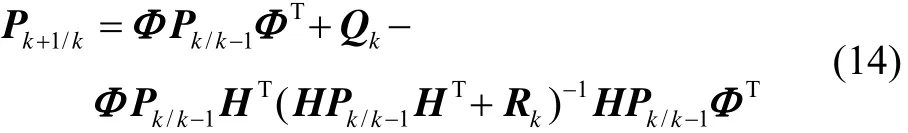
考虑建模误差，准确系统模型可表示为

式中：Δc是CW方程递推常值偏差。

递推，得到系统状态的一步预测估计：

此时，系统真实状态：

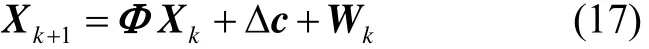
得到估计状态的真实误差：

对导航算法的有偏性进行分析，对式(18)取期望，得：

对上式展开，状态估计的期望偏差为

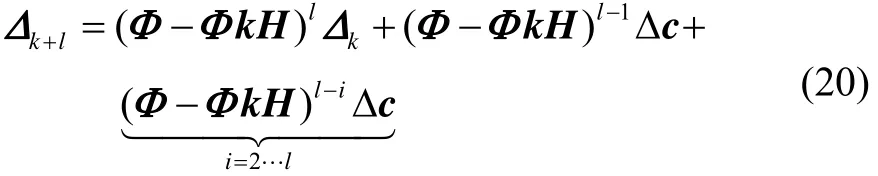
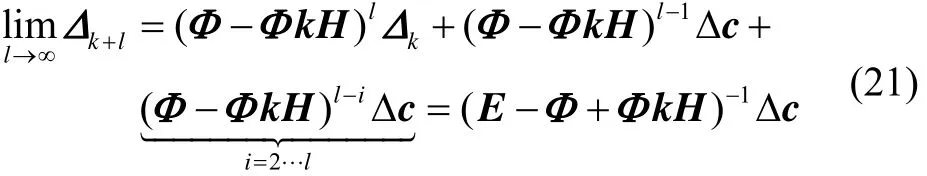
根据式(18)和(20)，一步预测状态的真实方差可表示为

式(23)分解为两个部分。均值可以通过式(21)计算，随机部分方差是递推方程，形式简单，方便实现其稳态值的求解。式(22)(23)理论上解决了基于CW方程的相对导航算法滤波性能分析问题。

由式(24)得，过程噪声Qk中σ2w与滤波精度的关系如图2所示。

研究表明，过程噪声是系统真实滤波性能的主要影响因素，对于特定的交会区间，过程噪声量级以及滤波性能均存在最优解（如图2所示的拐点处），合理设置过程噪声可以获得最佳滤波性能。

然而，如式(2)所示，中心引力场二次项误差随着距离增加线性平方增加，必然影响滤波器的全局最优性。根据式(24)进一步研究滤波精度随交会距离变化的特性，如图3所示。

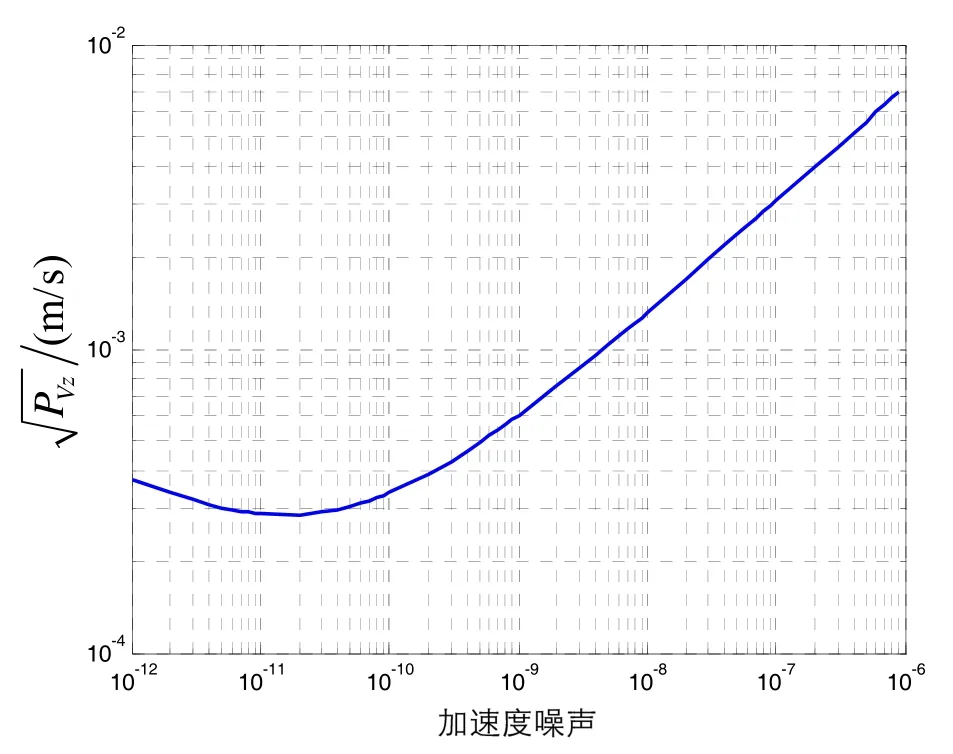
图2 过程噪声与滤波误差关系图（20 km）Fig.2 Relationship between process noise andfilter error (20 km)

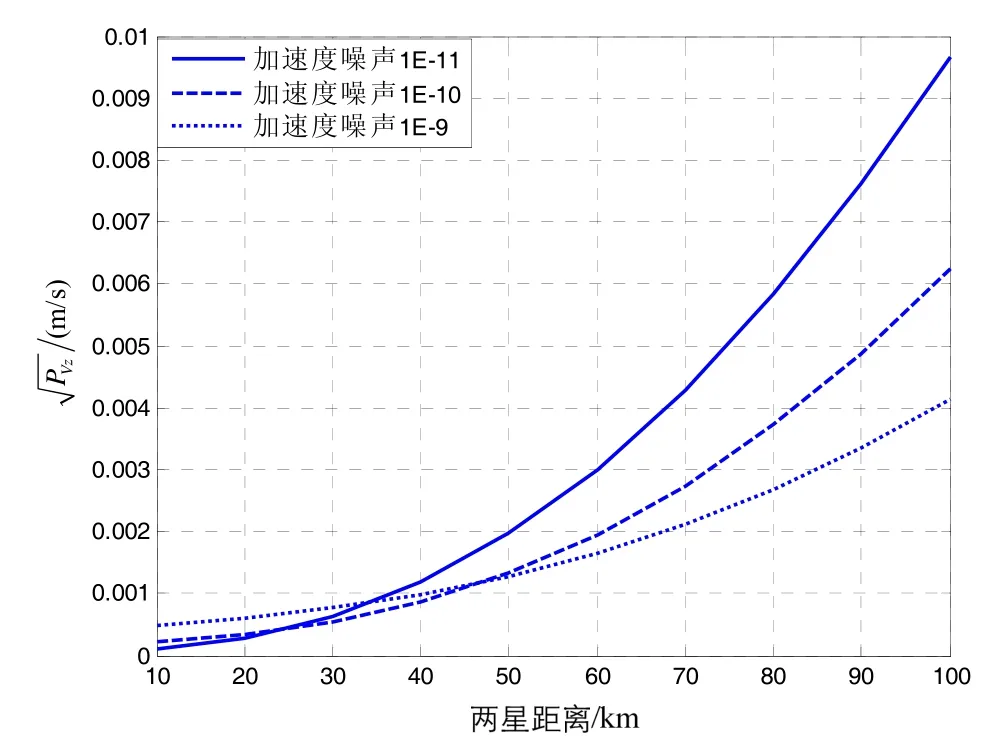
图3 滤波误差与相对距离关系图（10～100 km）Fig.3 Relationship between filter error and relative distance (10～100 km)

研究表明：滤波误差与交会距离正相关，交会距离越远，误差越大；同时相关性与过程噪声的量级有关，对于特定的轨迹，远程和近程的最优滤波性能不可兼得，远程的最优性能往往以近程的次优性能为代价。图3也为全局最优滤波器设计提供了定量分析的依据，分区间整定过程噪声可以实现全区域的最优滤波性能。

4 仿真验证

设计仿真试验，对静止轨道远程交会中相对导航EKF滤波算法性能进行验证。

雷达测量噪声如式(12)所示。

追踪星和目标星运行在静止轨道，两星相位差分别为由0.06°抵近至0.03°，两星相对距离约由50 km接近至20 km。

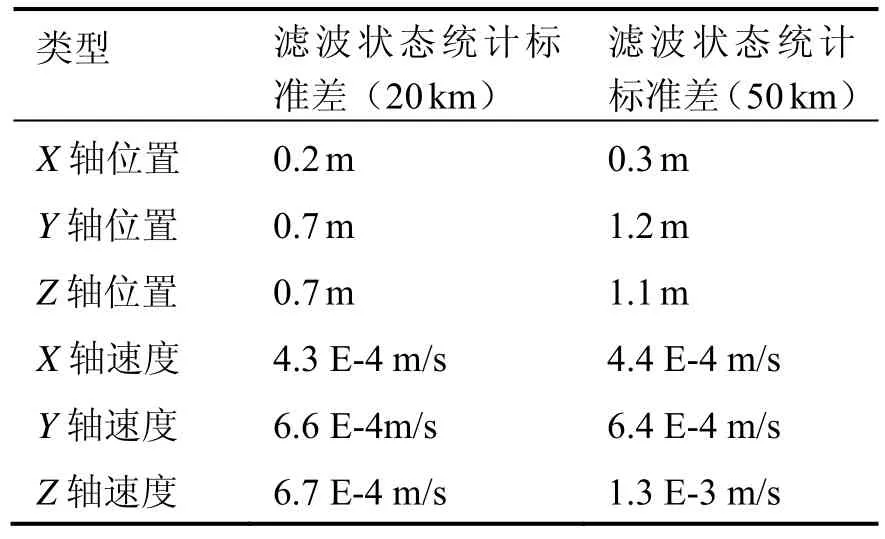
表1 相对导航滤波标准差Tab.1 Relative navigation filter standard deviation

仿真结果显示，20 km和50 km处Z轴相对速度项滤波精度分别为6.7E-4 m/s和1.3E-3 m/s，与图3（加速度噪声取点虚线）理论分析的数值一致。随着距离增加，滤波性能出现衰减，与图 3理论分析的趋势一致。

由于各轴的系统误差存在差异，在交会过程中滤波性能以及衰减趋势也存在差异。运动学方程误差分析表明，Z向的系统较大且存在常值误差，因此其位置及速度滤波误差随距离增加的衰减明显，与理论分析一致。

图4 两星相距20 km时的相对位置估计误差Fig.4 Relative position estimation error when the distance is 20 km

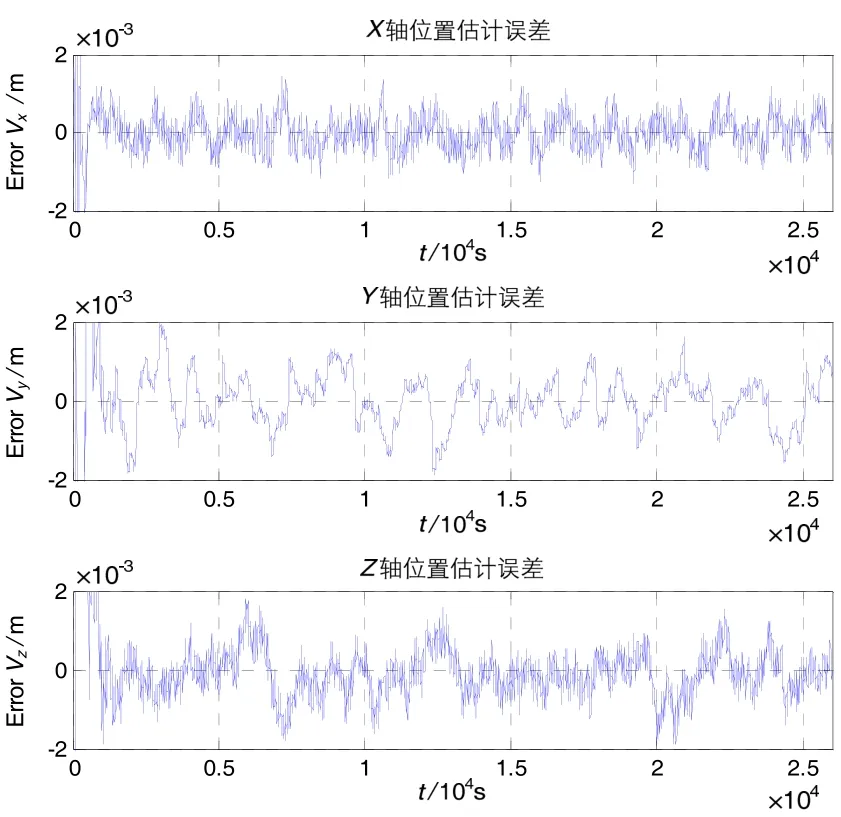
图5 两星相距20 km时的相对速度估计误差Fig.5 Relative velocity estimation error when the distance is 20 km

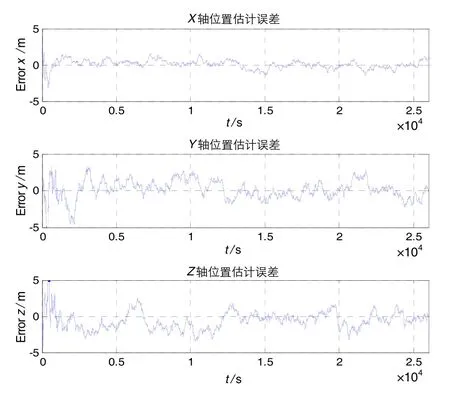
图6 两星相距50 km时的相对位置估计误差Fig.6 Relative position estimation error when the distance is 50 km

图7 两星相距50 km时的相对速度估计误差Fig.7 Relative velocity estimation error when the distance is 50 km

综合分析表明，系统的综合性能与系统噪声阵的配置相关，根据系统需求合理配置系统噪声阵，可保证系统性能满足远程交会各阶段精度要求。

5 结 论

针对地球静止轨道卫星远程交会过程中相对运动模型的系统误差特性，采用非线性转化建立基于间接测量的相对导航系统，推导模型误差的传递机理，给出了相对导航EKF算法的期望以及噪声特性的定量分析模型。研究表明：确定距离区间存在最优过程噪声量级及其对应的最优滤波性能；远程交会过程中，滤波误差与交会距离正相关，对于特定的相关轨迹，远程和近程的最优滤波性能不可兼得，远程的最优性能往往以近程的次优性能为代价，可作为全局最优滤波器的定量设计依据。仿真表明，分析结论是正确的，理论上解决了静止轨道远程交会过程中导航性能的量化评估问题。

（References）：

[1] Segal S, Gurfil P. Stereoscopic vision-based spacecraft relative satellite estimation[R]. AIAA-2009-6094, 2009.

[2] Zhang S J, Liu F H, Cao X B, et al, Monocular vision-based two-stage iterative algorithm for relative position and attitude estimation of docking spacecraft[J]. Chinese Journal of Aeronautics, 2010, 23(2): 204-210.

[3] 龚柏春, 罗建军, 马悦. 单测角相对导航的相对距离重构新算法[J]. 中国惯性技术学报, 2014, 22(3): 340-345. Gong Bai-chun, Luo Jian-jun, Ma Yue. Novel reconstructing algorithm of relative distances for angle-only relative navigation[J]. Journal of Chinese Inertial Technology, 2014, 22(3): 340-345.

Performance evaluation of relative navigation algorithm during geostationary orbit long-range rendezvous

REN Jia-dong1,2,3, ZENG Qing-shuang1, ZHU Hong1,3

(1. School of Astronautics, Harbin Institute of Technology, Harbin 150001, China; 2. Shanghai Aerospace Control Engineering Institute, Shanghai 201109, China; 3. Shanghai Key Laboratory of Space Intelligent Control Technology, Shanghai 201109, China)

Long-range autonomous rendezvous is crucial to the precise placemen of geostationary collocation satellites. Based on the analysis of error signal characteristics of relative motion model during large-span remote rendezvous process, the error transfer mechanism is theoretically derived. Then the quantitative analysis model of mean and noise characteristic is proposed for the relative navigation based on an extended Kalman filter (EKF) algorithm. The analysis results show that there exists an optimal process noise level and corresponding optimal filter performance with respect to the determining distance range. The estimation error is positively correlated with the intersection distance, which can be used as the quantitative basis to design a global optimum filter. Besides, it also theoretically provides an approach to quantitatively evaluate the navigation performance of the EKF optimal filter during long-range rendezvous of geostationary orbit. Simulation results demonstrate that the analysis results are correct, and the relative velocity estimation error is 0.005 m/s(1σ), which satisfies the mission requirements of orbit long-range rendezvous.

geostationary satellites; autonomous; long-range rendezvous; relative navigation; filter precision

V448.21

A

1005-6734(2016)02-0257-06

10.13695/j.cnki.12-1222/o3.2016.02.022

2015-12-15；

2016-03-28

国家高技术研究发展计划（863计划）（2015AA1073A）

任家栋（1986—），男，博士研究生，从事导航滤波技术研究。E-mail: renjiadong@126.com联 系 人：曾庆双（1963—），男，教授，博士生导师。E-mail: zqshuang2000@yahoo.com.cn