基于统计与遗传算法的Cook-Torrance模型研究

李明哲，　赵继广，　杨　帆

(1. 装备学院 研究生管理大队, 北京 101416；　2.装备学院 装备战略发展研究所, 北京 101416)



基于统计与遗传算法的Cook-Torrance模型研究

李明哲1，赵继广2，杨帆1

(1. 装备学院 研究生管理大队, 北京 101416；2.装备学院 装备战略发展研究所, 北京 101416)

摘要为解决Cook-Torrance模型在实际应用中存在偏差的问题，以航空铝板为研究对象，对比分析模型仿真数据和双向反射分布函数实验数据，通过对Cook-Torrance模型的镜面反射和漫反射两部分进行修正，提出一种Cook-Torrance模型的改进方法。对于模型镜面反射部分，采用遗传算法拟合了修正参数；对于模型漫反射部分，采用统计方法解算出其漫反射参数。仿真与实验结果对比表明:改进模型能够更加准确地描述不同波长铝合金和黄铜等金属材料的双向反射分布特性。

关键词航空铝板；Cook-Torrance模型；双向反射分布函数；遗传算法

Analysis on Cook-Torrance Model Based on Genetic Algorithm and Statistical Method

LI Mingzhe1，ZHAO Jiguang2，YANG Fan1

(1. Department of Graduate Management, Equipment Academy, Beijing 101416, China；2. Equipment Development Strategy Research Institute, Equipment Academy, Beijing 101416, China)

AbstractTo solve out the issue of the deviation of Cook-Torrance model in actual application, by taking aviation aluminum plate as the research object, the paper makes contrastive analysis on simulation data and experimental data of bidirectional reflectance distribution function, and brings out a way to improve Cook-Torrance model through correction of specular reflection and diffuse reflection of Cook-Torrance model. As to the specular reflection of the model, the paper fits correction parameters based on the genetic algorithm; as to diffuse reflection of the model, the paper solves out the diffuse parameters with statistical method. Simulation and experimental result shows, the improved model can describe the bidirectional reflectance distribution characteristics of metal materials such as aluminum and brass with different wavelengths more accurately.

Keywordsaviation aluminum plate; Cook-Torrance model; bidirectional reflectance distribution function (BRDF); genetic algorithm

铝合金是飞机轻量化的首选材料[1]，在航空领域具有不可替代的作用，在各种飞机上都有普遍地应用，特别是在军用飞机中用量最高达60%，且一直被用于无人机的主梁和发动机机舱[2]。作为飞机的重要组成材料，航空铝材的各方面特性已经成为研究的焦点。故本文选取飞机材料中最为常见的航空铝板作为研究对象。BRDF是表征目标光学散射特性的重要参数。Cook-Torrance模型是一种常见的BRDF模型，能够对目标材料的镜面反射和漫反射进行全面分析。相对于其他模型，该模型具有适用材料多和计算量小的优势，因此在计算机图形学中得到了十分广泛的应用[3-6]。但受制于模型参数的设置，Cook-Torrance模型在描述航空铝板的光学特性时存在较大偏差。为充分利用该模型的优势，基于实验分析提出了一种Cook-Torrance模型改进方法以弥补其不足。

本文首先从航空铝板材料入手，分析得知Cook-Torrance模型仿真结果与BRDF实验结果之间的偏差具有可分离为镜面反射部分和漫反射部分的特点。然后基于实验数据分别对Cook-Torrance模型的镜面反射部分和漫反射部分进行修正与优化，并根据遗传算法和统计平均方法计算获得修正模型的参数，进而得到改进的Cook-Torrance模型。最后在不同材料和不同波长下，对改进的Cook-Torrance模型进行验证。该方法对准确建立不同材料的Cook-Torrance模型具有重要的借鉴意义。

1Cook-Torrance模型概述

Cook-Torrance模型[3]采用微面元的方法对目标表面进行研究。该模型计算公式为

(1)

式中，R为BRDF值，单位为(sr)-1；Rs为BRDF镜面反射分量；Rd为BRDF漫反射分量。

漫反射分量为

(2)

式中，ρ为目标材料的方向半球反射率；Kd为漫反射分量所占的比例。

镜面反射分量为

(3)

式中，F为菲涅耳反射系数；D为表面高低起伏分布函数；G为遮蔽因子；θi为入射角；θr为探测角；Ks表示镜面反射分量所占的比例，且有Ks+Kd=1。

2铝合金表面Cook-Torrance模型仿真数据的偏差分析

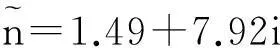
按照以上方法共进行了16×16×33=8 448组实验。为了便于统一分析，将得到的8 448组BRDF值按照如下方法进行排列：首先固定θi的值，再遍历θr的值;此时每取一个θr的值，则遍历一次φ的值，最后以此作为循环过程再遍历θi的值。具体流程图如图1所示。图中Number为对应于每一组角度的序号。

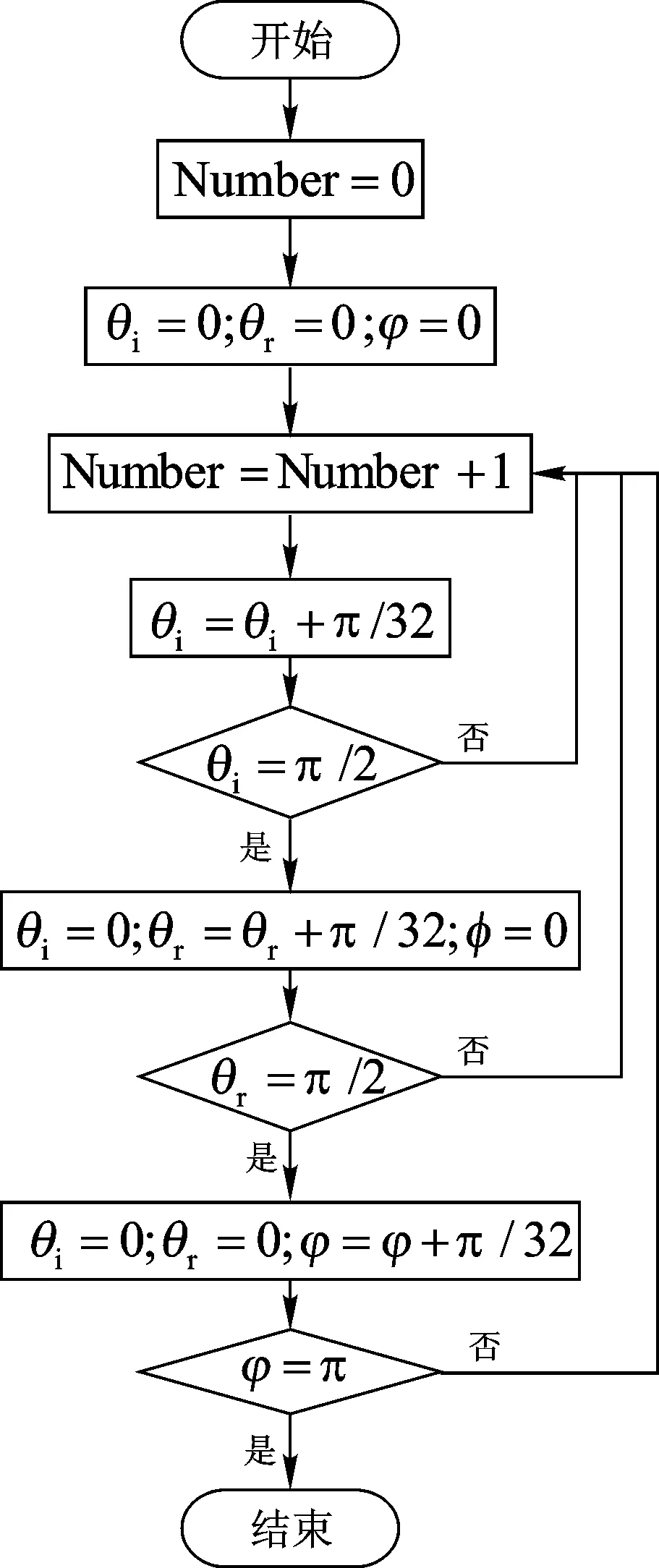
图1　角度排列流程图

按照图1所示的流程顺序，BRDF仿真结果如图2所示，其中横坐标Number为序号，纵坐标为BRDF值，单位为(sr)-1。由图2中排序后的BRDF值，可以看出BRDF仅在若干个离散点处具有明显的非零值。进一步分析，图2中共有16个极大值点，它们对应的角度均为方位角φ=π，且入射角等于探测角(θi=θr)。为分析方便，将满足条件φ=π和θi=θr的16个点提取出来进行分析，如图3所示。为表述方便，称其为BRDF镜面反射线，其中横坐标为入射角θi，单位为(°)。

图2　排序后的BRDF仿真结果

图3　仿真得到的BRDF镜面反射线

为了对Cook-Torrance模型进行研究，采用REFLET 180测量仪对航空铝板的真实BRDF值进行实验测量。REFLET 180测量仪可以对目标进行全方位自动扫描和测量，快速获得不同入射角、探测角和方位角下目标的BRDF值。

将BRDF值按照图1所示流程进行排列，结果如图4所示。提取其中的BRDF镜面反射线如图5所示。

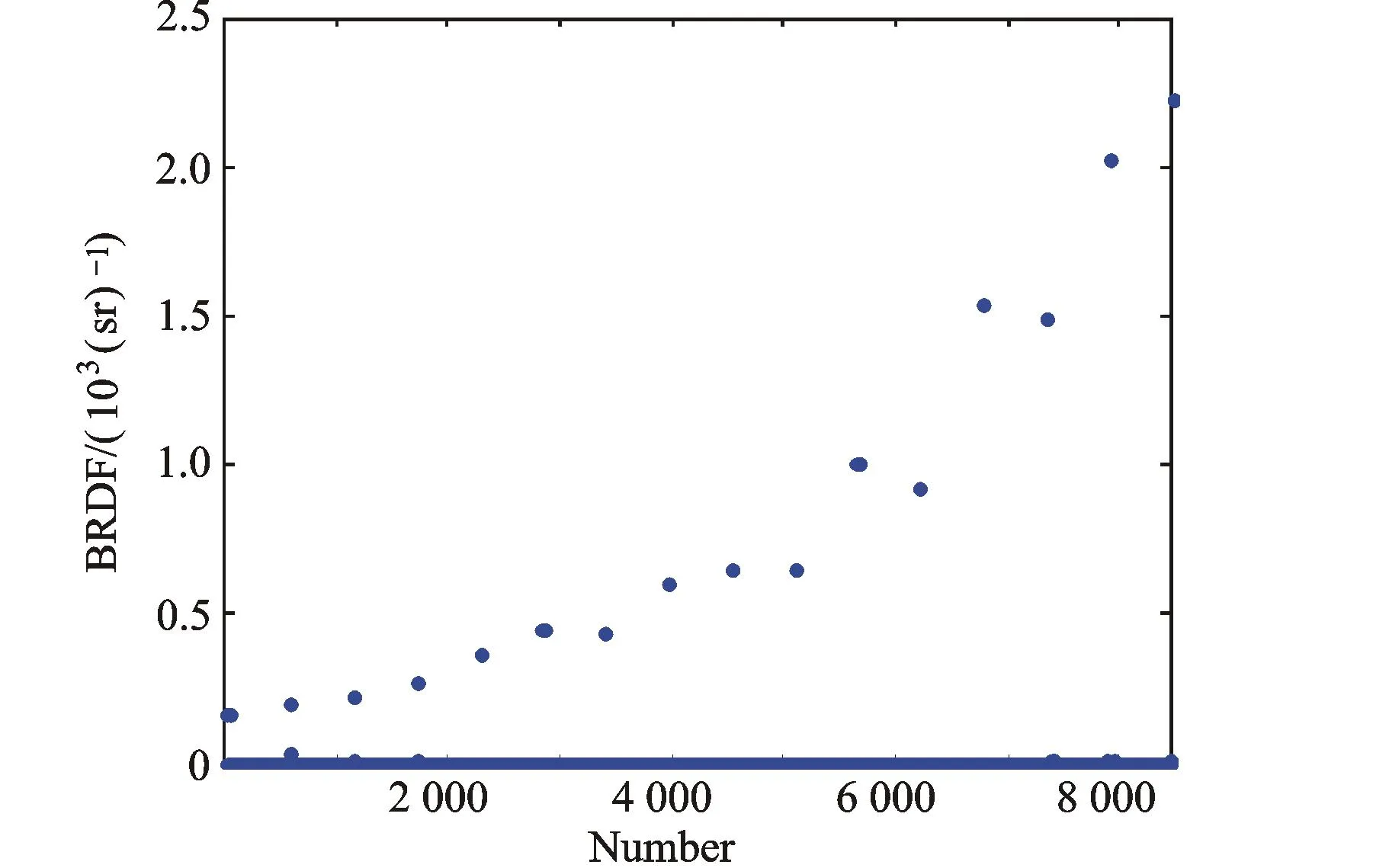
图4　排序后的BRDF值

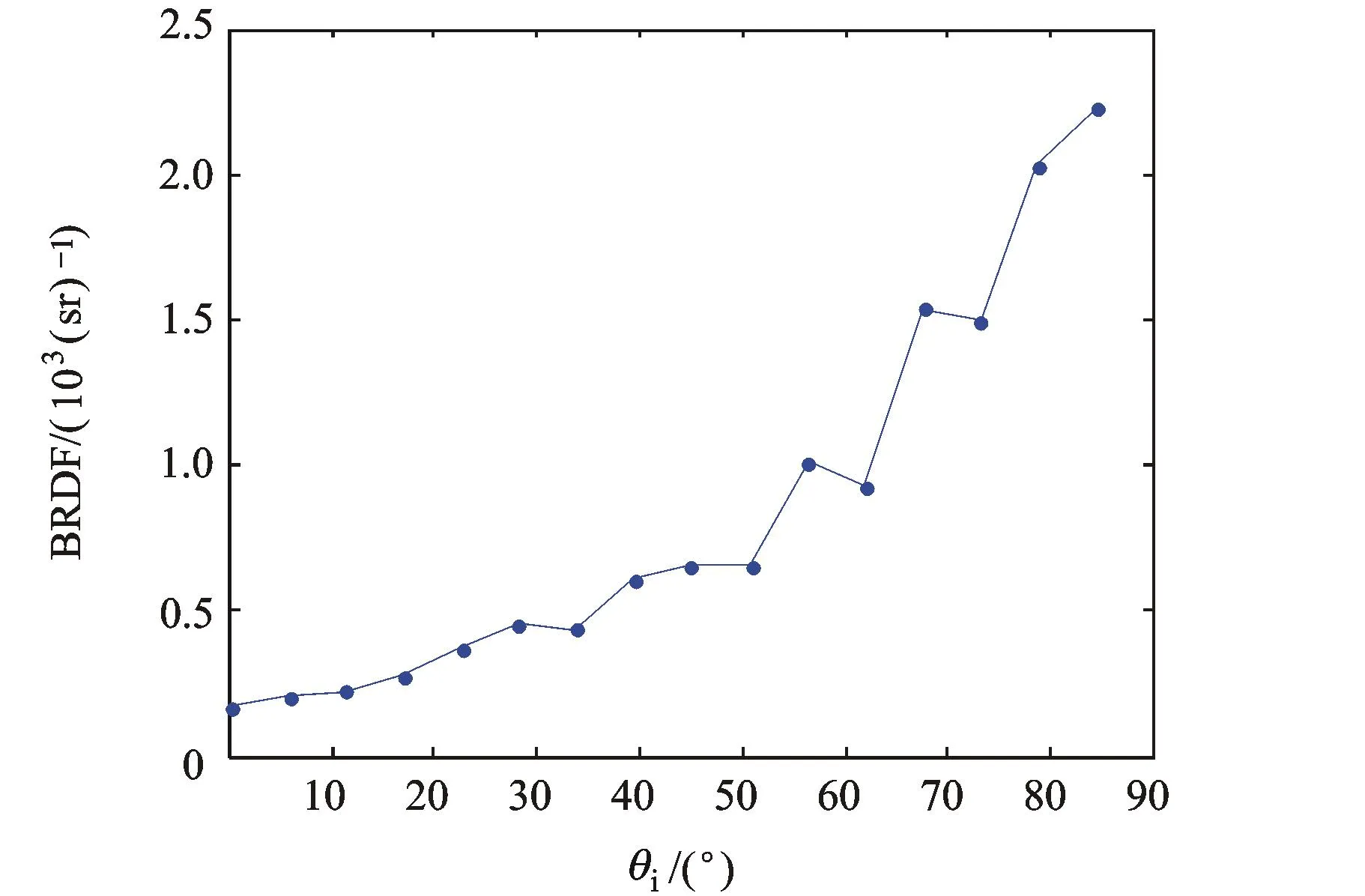
图5　实验得到的BRDF镜面反射线

对比图2与图4可知，仿真结果相对实验结果存在较大偏差。图3中仿真得到的BRDF镜面反射线与图5中实验得到的BRDF镜面反射线具有明显不同的变化趋势。通过研究发现，这一部分偏差主要由于Cook-Torrance模型将每一个微面元近似为理想的光滑表面进行研究，而实验中的材质较为粗糙，故不能准确地对其进行模拟。特别是当入射角较大时，入射方向与目标表面趋于平行，此时在目标材质表面的遮挡效应和多次散射作用十分明显，对BRDF值产生较大的影响。此外，虽然Cook-Torrance模型具有比较广泛的适用范围，但不可能对每一种材料的BRDF值都十分准确地描述，即总是会存在不同程度的偏差。因此考虑从实验数据出发，针对所研究的材质对模型进行一些必要的修正和改进，以使得模型能够更准确地描述该材质的双向反射分布特性。

3Cook-Torrance模型改进方法研究

图3和图5中的16个数值可以表示镜面反射对BRDF值的贡献，而漫反射对BRDF值的贡献则可以由非镜面反射方向的BRDF值来表示。由图2和图4可以看出，相对于镜面反射而言，漫反射分量非常小，故在考虑镜面反射时，漫反射部分可以忽略不计；而在考虑漫反射时，由于其值接近于零，且理想的漫反射与角度无关，则可以将其视为常值。因此，从BRDF镜面反射分量和BRDF漫反射分量两部分对模型改进方法进行研究。

3.1基于遗传算法的Cook-Torrance模型镜面反射分量改进方法

分别将实验和仿真得到的BRDF镜面反射线进行对比，如图6所示。根据仿真数据和实验数据的BRDF镜面反射线变化趋势的不同，对BRDF镜面反射分量进行改进。

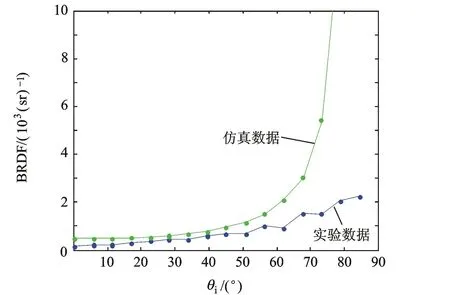
图6　Cook-Torrance模型仿真数据与实验数据对比图

对于镜面反射部分，可将Cook-Torrance模型简写成如下形式

Rs=FDGH

(4)

式中，H的表达式为

(5)

经分析，在F、D、G和H中，仅有F和H两项对镜面反射线有影响。由于F由经典公式——菲涅耳公式推导得到，具有明确的物理意义，故通过对H进行修正来实现对模型的改进[4]。由于航空铝板表面为各向同性表面，根据光路的可逆性，可得知入射角和探测角具有互易性，从而H是关于θi、θr对称的。

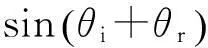
(6)

其次，考虑到此时2条镜面反射线的变化趋势仍然有明显不同，于是在分子和分母项各加入一个常数项来修正曲线的细节走势，使得仿真曲线与实验曲线的拟合情况更加理想，系数分别设为a和b，则有

(7)

最后，考虑到幅值的倍数差异，引入一个因子c，最终得到改进的H表达式为

(8)

对于所选的航空铝板材料，为了得到a、b、c的值，采用遗传算法[5-6]进行参数拟合。以实验数据和仿真数据比值的均方差E作为遗传算法的适应度函数，其具体形式为

(9)

式中，Rept和Rsim分别为实验数据和仿真数据；Mavg表示实验数据与仿真数据比值的算数平均值。

通过遗传算法进行参数拟合得到，当a=0.849 2，b=0.257 6，c=0.434 7时，E取最小值。故最终得到

(10)

改进的Cook-Torrance模型镜面反射部分为

(11)

3.2基于统计方法的Cook-Torrance模型漫反射分量改进方法

在国内外的BRDF模型[7]中，常将物体表面的漫反射假设为理想漫反射进行研究。由于本实验结果中大部分非镜面方向的BRDF值接近于零，故假设模型的漫反射分量为理想的漫反射，并将通过统计平均方法得到的非镜面反射BRDF平均值作为BRDF模型的漫反射分量。对于漫反射部分的改进主要针对模型参数进行化简。

先对实验数据进行处理，通过对BRDF实验值与改进的Cook-Torrance模型镜面反射分量做差的方法剔除镜面反射的部分，仅留下非镜面反射值。在选取BRDF非镜面反射值计算漫反射分量时，由于设备自身的探测器具有一定的测量范围，因此镜面反射并不完全发生在θi=θr的情况下。

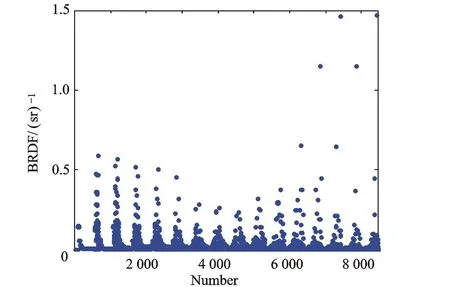
图7　BRDF漫反射分量实验值

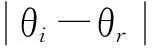
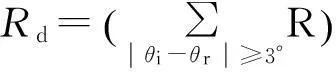
(12)

先前在对Cook-Torrance模型镜面反射部分进行改进时，去除了镜面反射比例参数Ks的影响，从而使得漫反射比例参数Kd变成了一个独立的参数。因此在对Cook-Torrance模型漫反射分量进行改进时，进一步通过将Cook-Torrance模型漫反射分量中的参数Kd·ρ设为e，使模型形式相对于经典Cook-Torrance模型进一步简化。简化后BRDF漫反射分量形式如下:

(13)

对于所研究的航空铝板，其中e=0.014 9π=0.046 8。通过以上对Cook-Torrance模型改进方法的研究，最终得到改进的Cook-Torrance模型为

(14)

基于航空铝板的改进Cook-Torrance模型为

0.046 8/π

(15)

4改进Cook-Torrance模型验证

由图7可以看出，BRDF漫反射实验数据均不超过1.5，而改进模型的漫反射仿真值为Rd=0.014 9，因此BRDF漫反射实验数据与改进模型仿真数据的最大差值同样不超过1.5。为了进一步直观分析改进Cook-Torrance模型的效果，按照图2的排列顺序，仿真结果与实验结果之差的绝对值Rminus如图8所示，其中星点代表镜面反射对应的点。图8中94.79%的值满足Rminus<0.1，此时仿真结果与实验结果拟合效果比较理想，而其中差异较大的部分主要由星点构成。因此接下来将BRDF镜面反射线提取出来进行对比分析，如图9所示，其中实线为仿真结果，星点为实验结果。

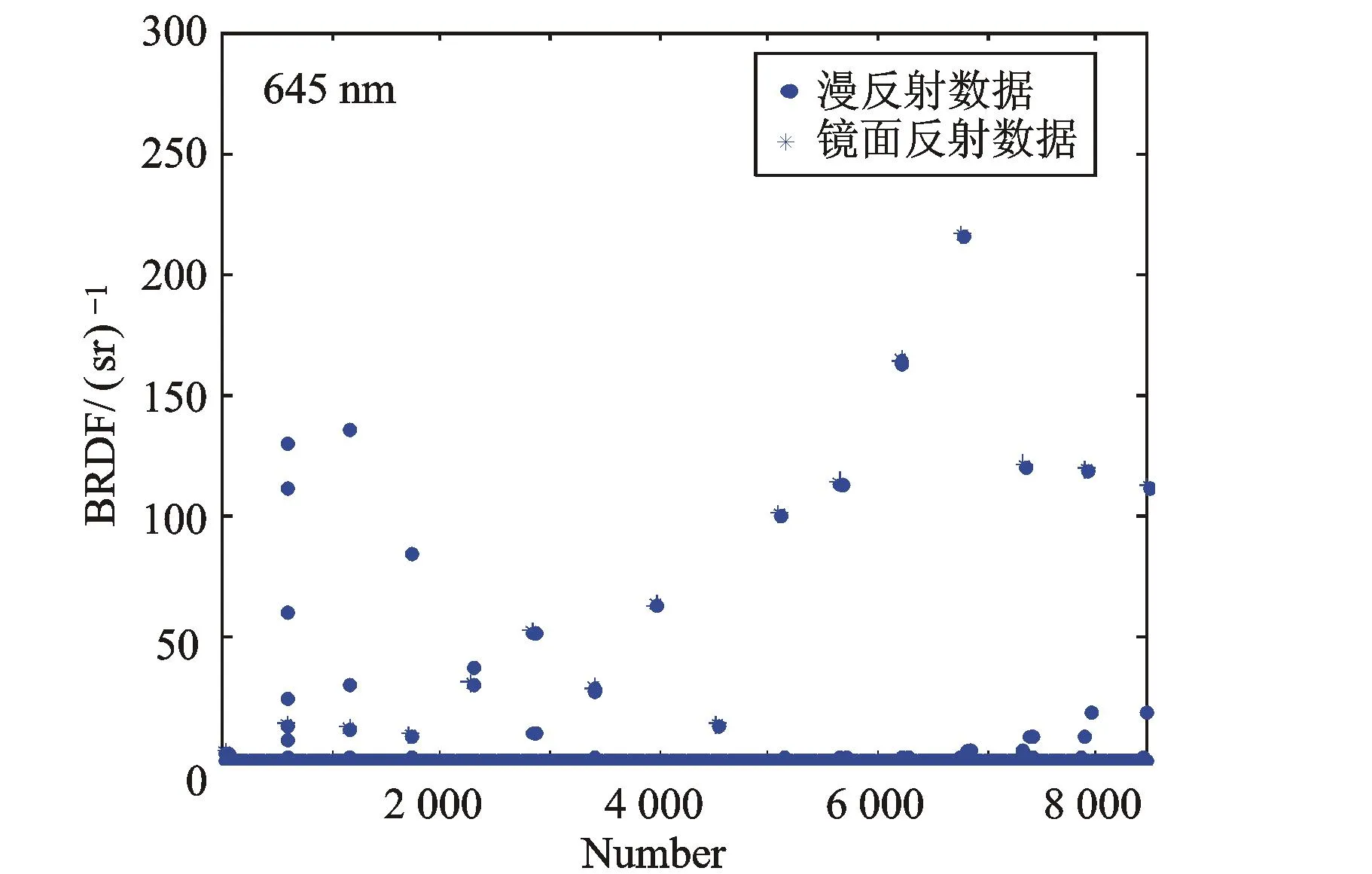
图8　改进模型仿真结果与实验结果之差

通过图6与图9对比可发现，相比于经典Cook-Torrance模型，改进后的模型仿真结果对实验得到的BRDF镜面反射线具有非常理想的拟合效果。为了对该模型改进方法进一步验证，分别在525 nm波长的典型绿光和445 nm波长的典型蓝光下，将经典Cook-Torrance模型和改进Cook-Torrance模型的仿真数据与实验数据进行对比分析，如图10和图11所示。

图9　改进后的Cook-Torrance模型仿真与实验镜面反射线对比图

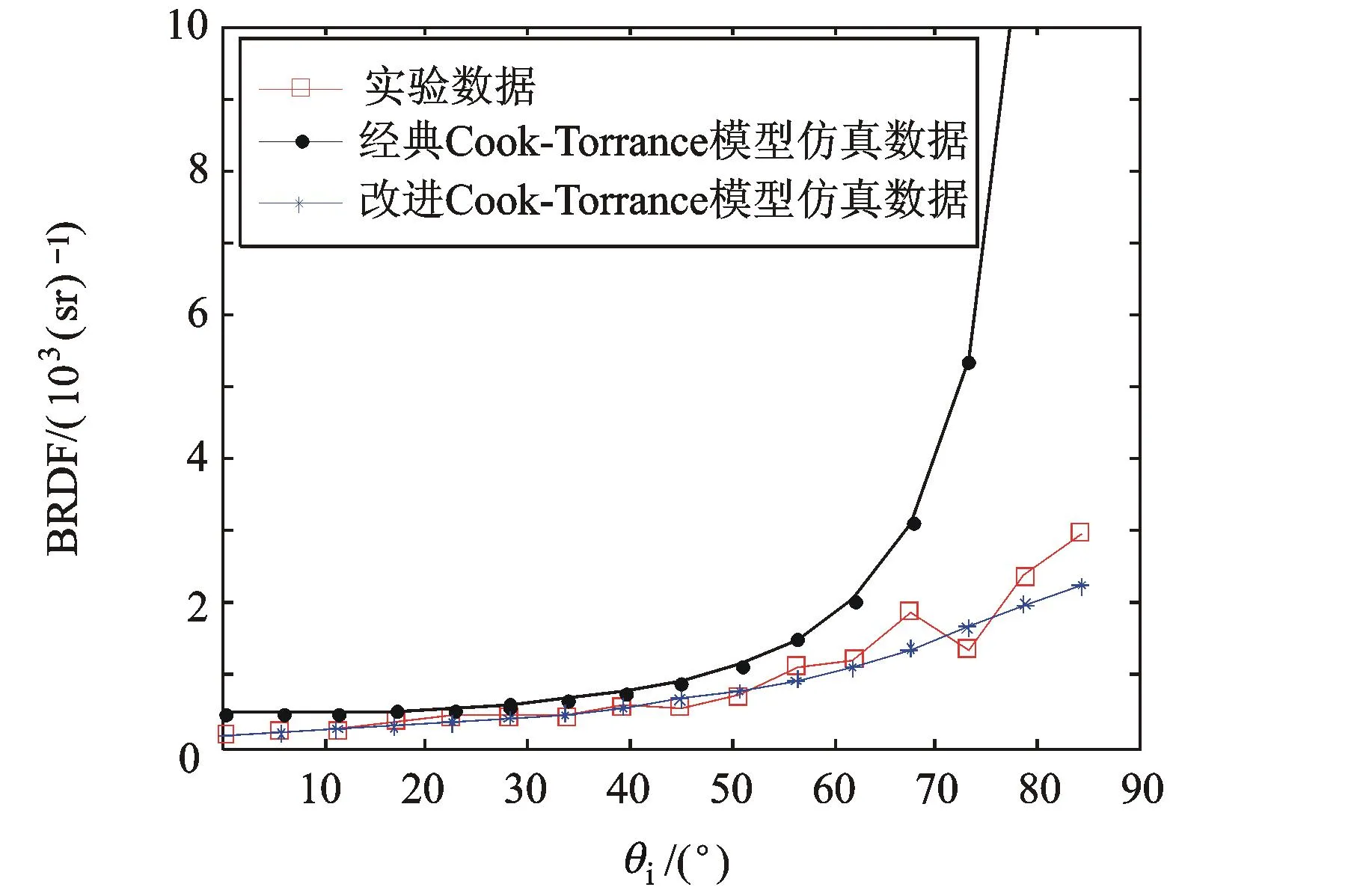
图10　525 nm波长下BRDF镜面反射线对比图

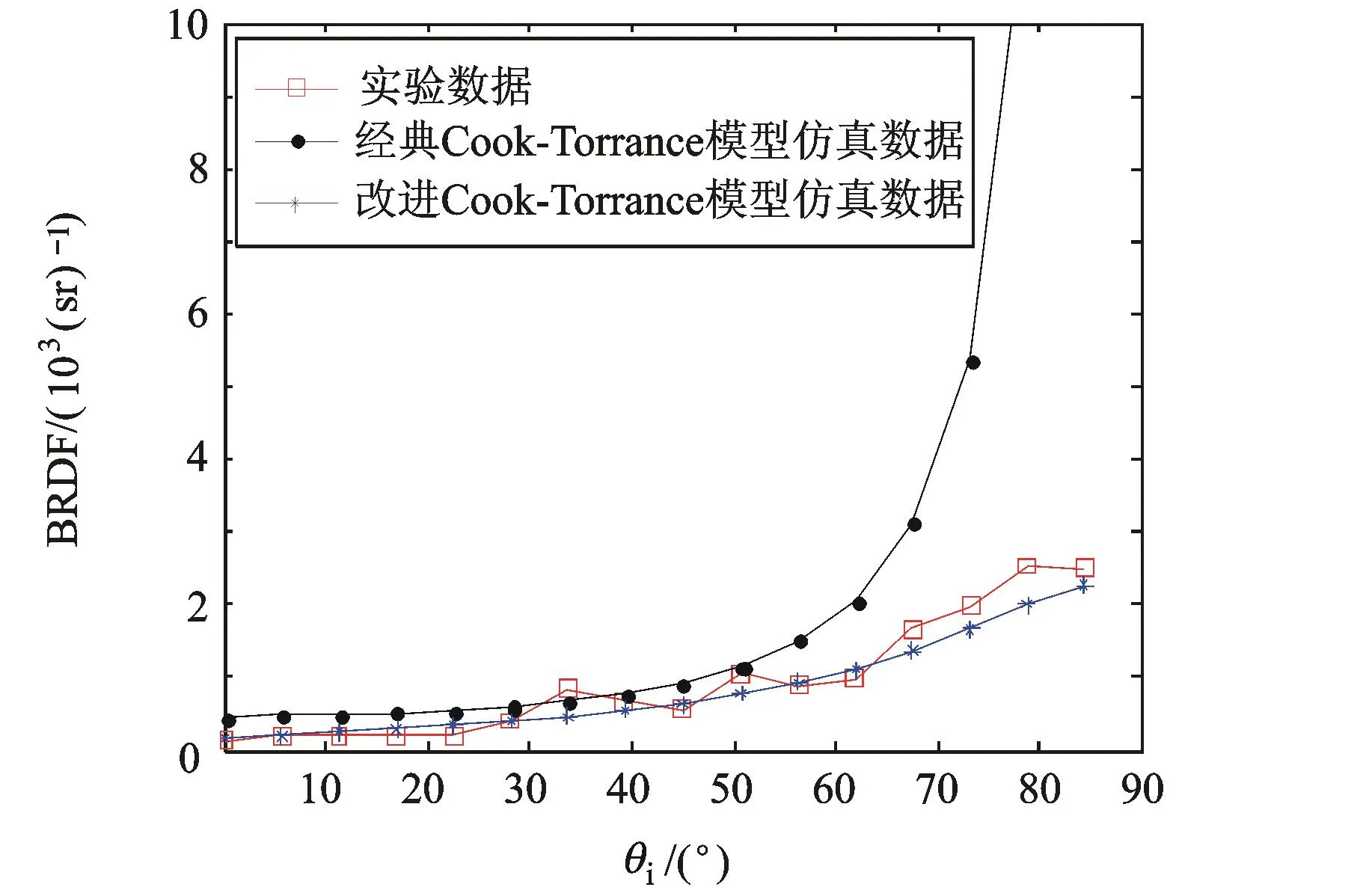
图11　445 nm波长下BRDF镜面反射线对比图

由图10和图11中BRDF镜面反射线的对比可以看出，改进的Cook-Torrance模型修正了BRDF镜面反射线的变化趋势，特别是当入射角度大于60°时，对实验数据的拟合程度有了显著地提升。

为进一步验证改进方法的正确性，再选取一种黄铜材料，分别在645 nm、525 nm和445 nm情况下进行验证。经遗传算法和统计方法计算得到改进Cook-Torrance模型参数a=0.795 0，b=0.132 7，c=0.811 0，e=0.017 3。经典Cook-Torrance模型和改进Cook-Torrance模型的仿真数据与实验数据进行对比分析如图12所示。

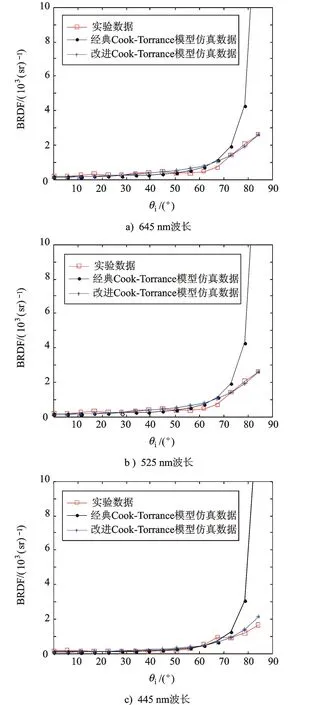
图12　不同波长下黄铜材料的BRDF镜面反射线对比图

通过图12可看出，由该方法得到的改进模型，对于研究黄铜材料也具有很好的效果。综合以上分析，充分说明了改进的Cook-Torrance模型可以实现对不同材料BRDF值分布情况更加真实准确的描述，也进一步验证了该模型改进方法的正确性。

5结 束 语

在645 nm的波长下，综合考虑了镜面反射和漫反射的情况对模型进行改进。通过对改进模型仿真结果的分析得到，相比于经典Cook-Torrance模型，改进的Cook-Torrance模型可以更好地模拟和分析航空铝板的双向反射分布特性。并对不同波长和不同材质分别做进一步的验证，验证结果表明，对于铝合金和黄铜等金属材质，改进模型的仿真结果较为理想。

Cook-Torrance模型的改进方法具有很重要的应用价值。对于不同的材料，经典Cook-Torrance模型经常会存在不同程度的偏差。通过引入的模型参数a、b、c、e来代替原有参数Ks、Kd和ρ，得到了一个满足互易性的四参数改进模型。该改进模型计算量小，且具有更广的适用范围和更高的准确度，同时在一定程度上克服了模型适用范围的限制给工程实际问题带来的复杂和冗余。此外，该方法为BRDF模型的改进工作提供了一条可以参考的途径，对该Cook-Torrance模型改进方法的深入研究与验证，将成为下一步工作的内容。

参考文献(References)

[1]文献军.铝合金价格走势及对航空制造业的影响[C]//中国航空工业产业链发展论坛会议论文集.北京：中国航空学会,2006：55-58.

[2]文武,杨晓波.无人作战系统之十七：蓄势待发英国“雷电之神”隐形无人机[J].轻兵器,2010(20):13.

[3]COOK R L,TORRANCE K E.A reflectance model for computer graphics[J].ACM Transactions on Graphics (TOG),1982,1(1):7-24.

[4]LI M Z,ZHAO J G,ZHOU Y T.Analysis of the modification method for Cook-Torrance model[J].Applied Mechanics and Materials，2014，556-562:4240-4243.

[5]李飞,张元志,王贻坤,等.基于实数遗传算法的混浊介质光学参数提取[J].光学学报,2013(12):198-206.

[6]唐运海,吴泉英,陈晓翌,等.基于遗传算法的渐进多焦点镜片子午线优化设计[J].光学学报,2014(9):245-251.

(编辑：李江涛)

中图分类号O432

文章编号2095-3828(2016)01-0116-06

文献标志码A DOI10.3783/j.issn.2095-3828.2016.01.024

作者简介李明哲(1990-)，男，硕士研究生，主要研究方向为目标光学特性分析。

基金项目部委级资助项目

收稿日期2015-01-16