畸变电流下的电子脱扣器校准误差分析
2016-04-12牛纯春赵莉华冯政松牛帅杰付荣荣
牛纯春,赵莉华,冯政松,牛帅杰,付荣荣
畸变电流下的电子脱扣器校准误差分析
牛纯春,赵莉华,冯政松,牛帅杰,付荣荣
(四川大学电气信息学院,四川 成都 610065)
畸变电流会引起电子脱扣器误动作,进而导致低压断路器无故跳闸。利用峰值系数KP和波形系数KW,分析了三角波和矩形波这两种典型的畸变电流波形对不同电流检测及控制处理方式电子脱扣器的影响,克服了谐波电流总畸变率(THD)难以准确、定量分析谐波电流对电子脱扣器校准误差影响的缺陷。通过峰值检测校准误差曲线和均值检测校准误差曲线可以准确、直观地看出不同畸变波形下峰值检测和均值检测的校准误差。根据非线性负荷的波形特征及校准误差曲线,适当地调整动作电流整定值,能够在一定程度上避免畸变电流导致的电子脱扣器频繁误动作现象。
电子脱扣器(ETU);畸变电流;峰值检测;均值检测;校准误差
0 引言
近年来,许多工厂和企业都发生过脱扣器非故障动作导致低压断路器无故跳闸问题,由此引发的停电事故,不仅威胁设备和人身安全,而且造成了严重的经济损失。调查发现,这些低压配电网的负荷主要为大容量UPS、变频调速电机、整流器、电弧炉等典型的非线性负荷,它们在工作过程中电流会产生严重的畸变,这是导致脱扣器非故障动作的主要原因之一。IEEE电力系统可靠性委员会也曾对低压断路器的可靠性进行了调查,结果表明断路器脱扣器的脱扣校准故障率最高,为其他故障(机械故障、电触头故障)的2倍甚至更高[1]。低压断路器脱扣器可分为热磁脱扣器、电子脱扣器以及智能脱扣器,目前在用的低压断路器中使用最多的仍是电子脱扣器。文献[2]指出,电子脱扣器能否用在电流发生畸变的情况下,取决于其电流检测方法,因为不是所有的方法都能检测电流的有效值(又称方均根值或RMS值)。常见的峰值传感器和均值传感器均不能准确反映畸变情况下电流的有效值。国内外已经有针对低压断路器脱扣器的研究,主要集中在以下几个方面:一是电压暂降或失压对脱扣器的影响[3-4],二是低压断路器脱扣特性仿真分析[5],三是低压断路器脱扣器的可靠性分析[6],四是智能脱扣器设计[7]。畸变电流对电子脱扣器动作特性影响方面的研究还较少,且主要为定性分析[8]。低压配电网中大容量非线性负荷的种类和数目越来越多,电流畸变日益严重[9-11],这对普通电子脱扣器的动作准确性是一个巨大的威胁。所以,定量分析畸变电流对电子脱扣器校准误差的影响具有重要意义。
本文基于三段电流保护特性曲线来说明电子脱扣器的电流保护原理,针对常用的峰值电流检测和均值电流检测方式,利用峰值系数 KP和波形系数KW两个特征量,定量分析了两种典型畸变电流(三角波和矩形波)情况下两种检测方式的脱扣校准误差,得到峰值检测校准误差曲线和均值检测校准误差曲线。指明了通过谐波畸变率(Total harmonic distortion,THD)来分析畸变电流下电子脱扣器校准误差的误导性。校准误差曲线可作为畸变电流下电子脱扣器动作值整定的重要依据。
1 电子脱扣器保护特性
电子脱扣器的保护特性包括:三段式电流保护,欠电压保护,单相接地保护,单相金属性短路、三相不平衡电流和发电机的逆功率保护等。由于谐波电流主要影响其中的电流保护,所以在此仅讨论电子脱扣器的三段电流保护特性。
电子脱扣器具有过载长延时保护、短路短延时保护以及短路瞬时保护等三段电流保护特性,常用如图1所示的三段电流-时间特性曲线来描述[12],图中横坐标表示过电流(指有效值)倍数,纵坐标表示动作时间。脱扣器的额定电流In与被保护线路的计算电流Ic之间存在如下关系:

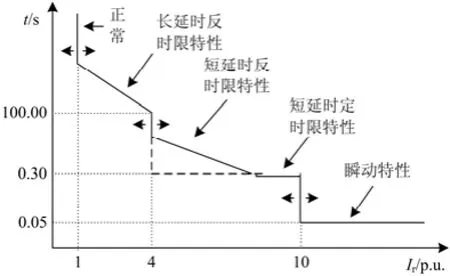
图1 三段电流保护特性曲线Fig. 1 Three-section protection characteristics curve of fault current
电子脱扣器三段电流保护的动作电流整定值和动作时间整定值均可调。过载长延时保护电流整定值Ir与In之间的关系为

短路瞬时保护具有定时限动作特性,动作时间为50 ms以内(一般为10~20 ms),短路瞬时保护电流整定值Ii为

当短路电流超过整定值时,瞬时保护立即启动。
短路短延时保护由反时限和定时限两部分组成,电流整定值Is为

一般以8Ir为分界点,当短路电流小于8Ir时,具有反时限动作特性;当短路电流大于8Ir时,具有定时限动作特性。定时限的动作时间一般为300 ms以内,反时限特性满足式(5)。
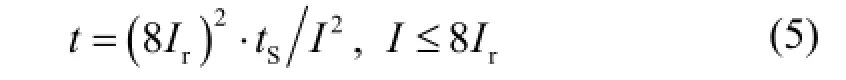
式中:t为动作时间;I为过电流值;tS为短延时整定时间。
过载长延时保护具有反时限动作特性,其数学表达式为
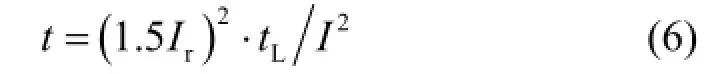
式(6)中:tL为长延时动作时间整定值;其余变量同式(5)中定义。
通过以上分析可知,电流保护的动作值都是基于电流有效值来设定的,准确计算出线路电流有效值是保护正确动作的必要前提。而目前在用的断路器电子脱扣器大多检测电流峰值或平均值,再按纯正弦波进行校准的方式得到线路电流的有效值。所以,当电流波形发生畸变时,会产生脱扣校准误差,导致过流保护或低阈值短路保护误动作。
2 典型非线性负荷波形分析
2.1 单相非线性负荷
单相非线性负荷广泛分布于商业和民用供电系统中,其中典型的有电子荧光灯、开关电源以及单相整流器等,图2给出了几种典型负荷的电流波形。电子荧光灯由于使用了电子镇流器,其输入电流波形发生严重畸变,波形如图2(a)所示,为明显的三角尖脉冲。个人计算机、打印机、电视机以及其他单相电子设备普遍采用开关电源,其交流侧电流 3次谐波含量很高,波形如图2(b)所示,呈现很短的尖脉冲。单相整流器为获得较平稳的输出电流,通常带有大电感,其输入电流波形如图2(c)所示,为矩形方波。
2.2 三相非线性负荷
三相非线性负荷广泛应用于工业和大型商业场所,典型的有大功率UPS、变频调速电机以及三相整流器等,图3给出了几种典型负荷的电流波形。
大功率UPS的输入侧电流会发生畸变,波形如图3(a)所示,呈现“双拱”形。变频调速电机在出力较大(低速)时的输入侧电流将产生严重的畸变,波形如图3(b)所示,呈现出“双三角”形。三相整流器直流侧有大电感时,输出波形较平稳,交流侧电流波形如图3(c)所示,呈近似的矩形方波。

图2 单相非线性负荷电流波形Fig. 2 Current waveforms of single phase nonlinear loads

图3 三相非线性负荷电流波形Fig. 3 Current waveforms of three phase nonlinear loads
2.3 畸变波形简化分析
通过分析典型非线性负荷的电流波形,按其特征可归纳分为两大类:一类是尖顶波,一类是平顶波。由于多数畸变波形的精确表达式难以求得,因此可采用分段线性化的方法来简化分析,如图4所示。
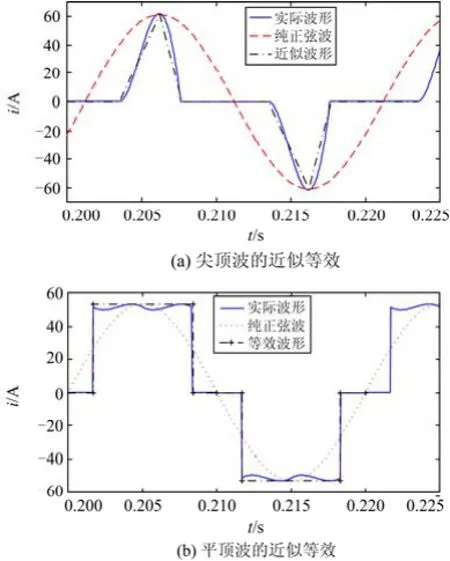
图4 波形的近似等效Fig. 4 Approximate equivalent of waveforms
图 4(a)所示的尖顶波与纯正弦波相比已产生严重畸变,用分段线性化的方法对其进行近似拟合,可等效为三角波。图4(b)所示的平顶波与纯正弦波相比也有明显畸变,同样用分段线性化的方法将其近似等效为矩形方波。
3 电子脱扣器校准误差定量分析
在分析畸变波形时,通常仅仅考虑 THD这一指标,而由 THD值只能定性说明谐波电流对电子脱扣器的影响,且具有一定的误导性(这将在本文第4节予以详细说明)。另外,文献[13]也指出,用THD表征电流畸变可能会造成误导。THD仅包含了谐波的幅值信息,而缺少相位信息,不能有效反映波形的外部特征(如波峰值)。所以,应选用其他指标来定量分析电子脱扣器的校准误差。
3.1 峰值系数KP和波形系数KW
图5所示为等效后典型电流畸变波形,其正、负半波镜对称。图中正半周波峰值为Ip,周期为T,半周导通时间为ton,三角波峰值出现时刻与起始导通时刻差值为t0,有效值为IRMS,正半周波均值为Iav。
则波形占空比为


图5 典型畸变波形Fig. 5 Typical distorted waveforms
峰值系数为
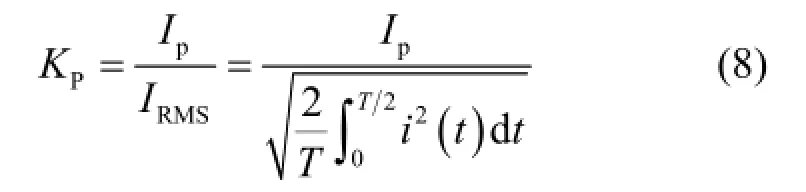
波形系数为
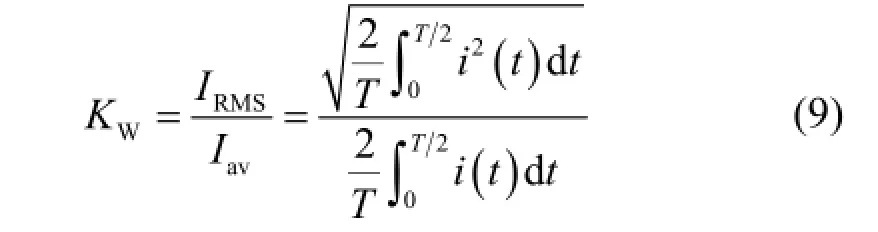
利用式(8)和式(9)可求得三角波和矩形波的峰值系数及波形系数两个特征量,它们只与波形占空比α有关。三角波、矩形波与纯正弦波的峰值系数和波形系数对比如表1所示。

表1 三种波形的参数对比Table 1 Parameter contrast of three waveforms
基于峰值检测的电子脱扣器通过检测到的电流峰值乘以系数K(通常为纯正弦波峰值系数的倒数,即 0.707)来得到电流有效值;基于均值检测的电子脱扣器通过检测到的均值乘以系数K'(通常为纯正弦波的波形系数,即1.111)得到电流有效值。对于标准正弦波,两种检测方法均能正确反映实际电流有效值,但当波形发生畸变时,两种方法所得到的电流有效值有很大误差,可能引起电子脱扣器误动作。峰值系数KP和波形系数KW两个特征量,分别反映了波形峰值和均值与有效值之间的关系,可用以定量分析畸变电流下基于峰值检测和均值检测两种电流检测方式的脱扣校准误差。
3.2 峰值因子PF和波形因子WF
为了直观、定量地分析畸变电流下电子脱扣器的脱扣校准误差,定义峰值影响因子(简称峰值因子)为

均值影响因子(简称均值因子)为

则有

由式(12)可以看出,电流有效值为峰值与峰值因子的乘积或均值与均值因子的乘积。
纯正弦波与两种典型畸变波的峰值因子对比如图6所示,当波形占空比α从0到1逐渐增大时,三角波和矩形波的峰值因子均单调递增。其中三角波的峰值因子始终小于纯正弦波的峰值因子(0.707);而矩形波在占空比 α小于 0.5时,峰值因子小于0.707;占空比α大于0.5时,峰值因子将大于0.707。
正弦波与两种典型畸变波的波形因子对比如图7所示,当波形占空比α从0到1逐渐增大时,三角波和矩形波的波形因子均单调递减。其中三角波的波形因子始终大于纯正弦波的波形因子(1.111);而矩形波在占空比α小于0.81时,峰值因子大于1.111;占空比α大于0.81时,峰值因子将比1.111略小。
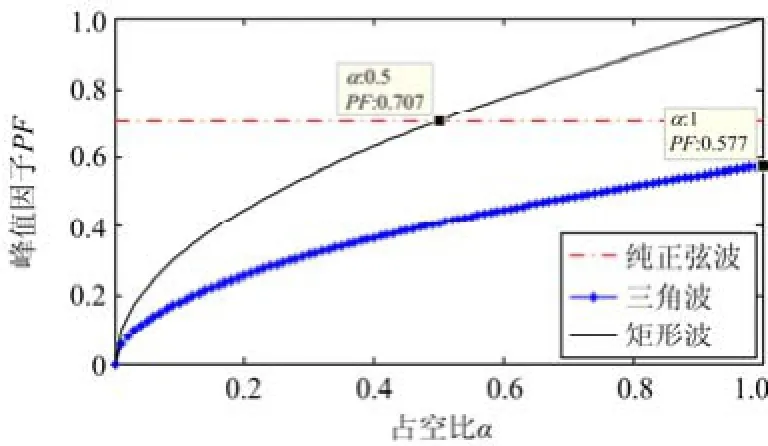
图6 三种波形的峰值因子对比Fig. 6 Peak factor comparison of three waveforms
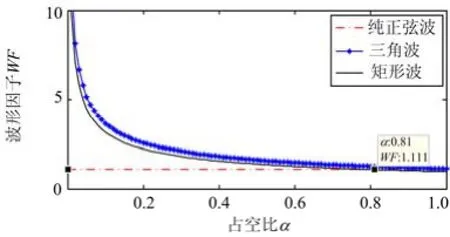
图7 三种波形的波形因子对比Fig. 7 Waveform factor comparison of three kinds of waveforms
3.3 校准误差分析
峰值检测校准误差可表示为

均值检测校准误差可表示为

式(13)和式(14)中的IRMS0、PF0、WF0分别为纯正弦波对应的电流方均根值、峰值因子、波形因子。由式(13)和式(14)可以求得峰值检测校准误差和均值检测校准误差,它们只与波形占空比α有关。
三角波和矩形波在不同占空比α下的峰值检测校准误差曲线如图8所示。三角波的峰值检测校准误差始终为正值,说明对三角波采用峰值检测并按标准正弦波进行校准求得的电流有效值比实际值偏大,并且随着三角波占空比的减小,峰值检测校准误差会越来越大。当占空比α为0.2时,误差已经达到了173.9%,即峰值校准得到的电流有效值是真实值的 2.739倍,这会被误认为是一个过流信号甚至是一个小短路信号,从而引起过载保护或低阈值短路保护误动作。
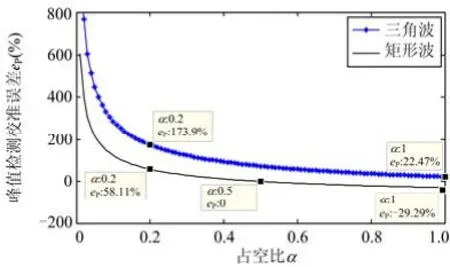
图8 峰值检测校准误差曲线Fig. 8 Calibration error curves of peak value detection
矩形波在占空比α小于0.5时,峰值检测校准误差为正,峰值校准得到的电流有效值比真实值大;当占空比α大于0.5时,峰值检测校准误差为负,表明峰值校准得到的电流有效值比真实值小。从图中还可以看出,矩形波的峰值检测校准误差明显小于三角波,当占空比α为0.2时才达到58.11%。
三角波和矩形波在不同占空比α下的均值检测校准误差曲线如图9所示。三角波的均值检测校准误差始终为负值,表明对三角波采用均值检测并按标准正弦波进行校准求得的电流有效值比实际值偏小,并且随着三角波占空比的减小,均值检测校准误差越来越大,当占空比α为0.2时,误差达到了-56.98%,即均值校准得到的电流有效值是真实值的0.430 2倍,这样的过流会被误认为是正常电流,从而使得过载保护拒动作。
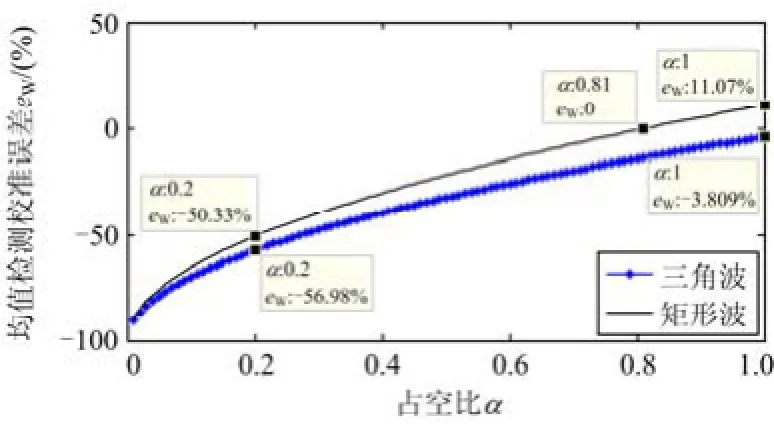
图9 均值检测校准误差曲线Fig. 9 Calibration error curves of mean value detection
矩形波在占空比α小于0.81时,均值检测校准误差为负,均值校准得到的电流有效值比真实值小;当占空比α大于0.81时,均值检测校准误差为正,表明均值校准得到的电流有效值比真实值大。从图中还可以看出,矩形波的均值检测校准误差略小于三角波,当占空比α为0.2时也达到了-50.33%,而且当占空比α为1时,矩形波出现最大为11.07%的正的均值校准误差。
由峰值检测校准误差曲线和均值检测校准误差曲线可得如下结论:
(1) 峰值检测校准误差和均值检测校准误差可统一为脱扣校准误差。对于三角波和矩形波而言,脱扣校准误差仅与波形占空比α有关,并且随占空比α单调变化。
(2) 脱扣校准误差为正值时,电子脱扣器检测到的线路电流有效值比真实值大,将会影响过载保护和低阈值短路保护,表现为脱扣器在正常工作电流下误动作。脱扣校准误差为负值时,电子脱扣器检测到的线路电流有效值比真实值小,将使脱扣器在过载电流下拒动作。
(3) 三角波具有正的峰值校准误差和负的均值校准误差,且误差绝对值随波形占空比α的减小而增大。矩形波的峰值校准误差和均值校准误差均有正有负,但在波形占空比α趋于0时的误差绝对值要比α趋于1时的误差绝对值大得多。
(4) 根据上述脱扣校准误差分析,可依据所带负荷类型适当调整电子脱扣器的电流保护整定值,以消除脱扣校准误差引起的保护装置误动作。
4 谐波总畸变率的误导性
下面将分别讨论利用三角波和矩形波的谐波总畸变率来分析电子脱扣器脱扣校准误差的误导性。对图5(a)所示的三角波,定义峰值偏移度β为
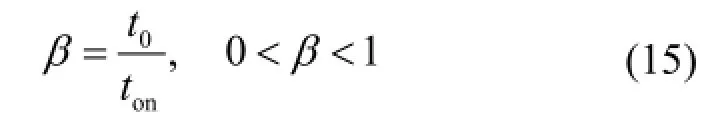
由高等数学基本知识可知,只要三角波的波形占空比α和峰值偏移度β恒定(即形状一定),则其谐波组成不变,总谐波畸变率也恒定。而起始导通时刻的变化(即波形的平移),实质为各谐波分量在不同的相位进行了叠加。
对占空比为α、峰值偏移度为β的三角波,将起始导通时刻作为计时零点,其傅里叶级数表达式为式中:
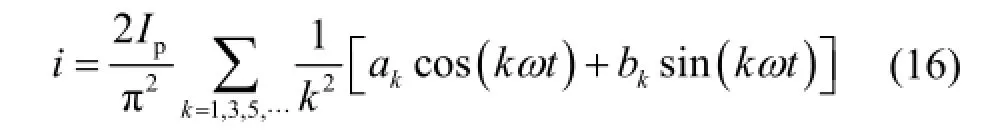

总谐波畸变率为
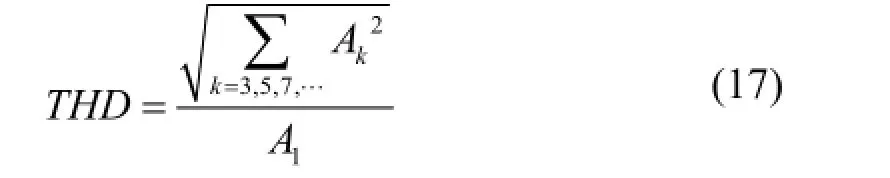
图 10给出了三角波总谐波畸变率与占空比 α及峰值偏移度β之间的关系。THD值随占空比α的增大而减小,同时关于峰值偏移度β=0.5对称。当α值较小时,THD值在β=0.5处最大;当α值较大时,THD值在β=0.5处最小。这样,同一个THD值可能对应多个α值;即使对于同一占空比α,THD值也可能不同。
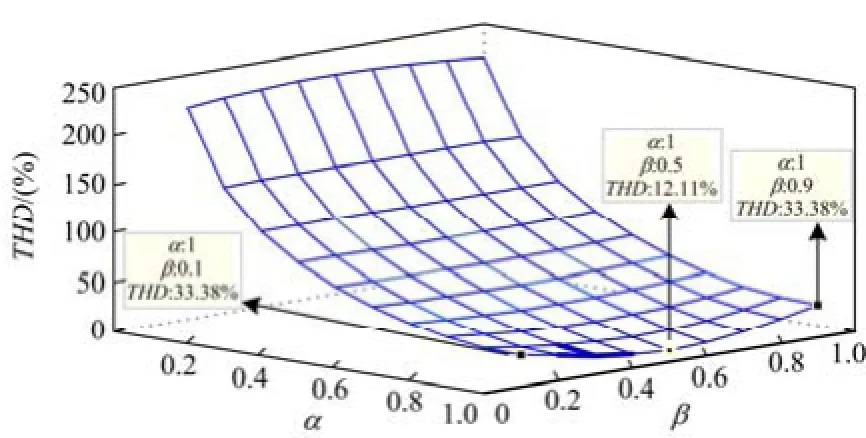
图10 三角波THD与a及β之间的关系Fig. 10 Relationship between THD, α and β for triangular wave
对图 5(b)所示的矩形波,占空比为 α,起始导通时刻为计时零点,其傅里叶级数表达式为
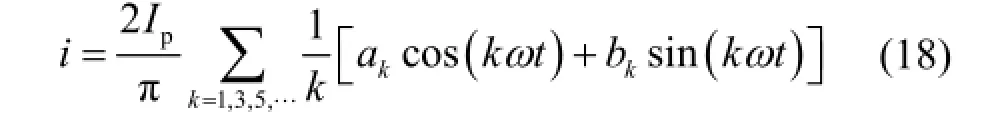
式中:
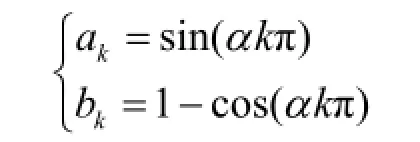
则总谐波畸变率为

式中,
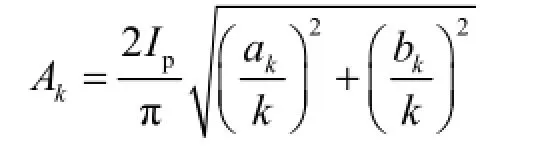
图 11给出了矩形波总谐波畸变率与占空比之间的关系。从图中可以看出,THD与占空比α有关,但非单调变化。α<0.74,THD值随着α的增大而减小;α>0.74,THD值随着α的增大而增大。这样,将会出现同一个THD值对应两个不同波形占空比α的情况。

图11 矩形波THD与α之间的关系Fig. 11 Relationship between THD and α for rectangular wave
从上面分析可知,对于三角波和矩形波,其波形系数、峰值系数及电子脱扣器脱扣校准误差均仅与占空比α有关,且存在一一对应关系,而总谐波畸变率与占空比α不是一一对应关系,即同一THD值可能对应多个不用波形占空比 α,亦即对应多个不同脱扣校准误差值。所以,通过总谐波畸变率THD的值来反映畸变电流下的脱扣校准误差,只能定性分析,且具有误导性。
5 实例分析
以工业中广泛使用的电弧炉负荷为例,分析畸变电流引起的脱扣校准误差。利用Matlab/Simulink搭建电弧炉系统的仿真模型[14],得到如图 12所示的电弧炉熔化期电流波形。
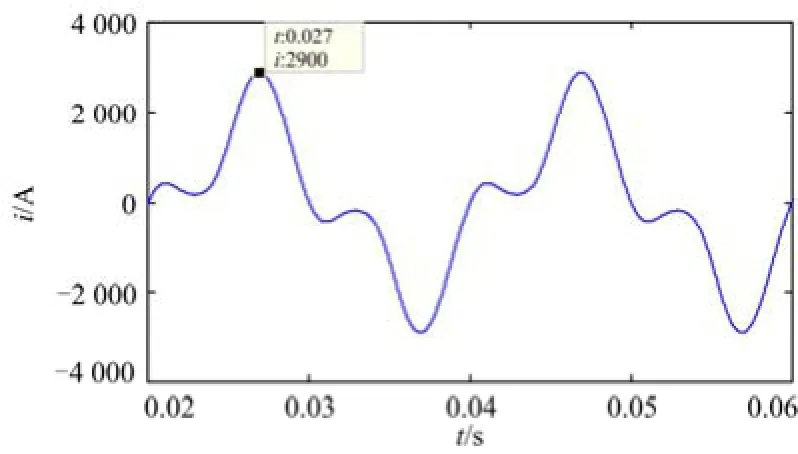
图12 电弧炉电流波形Fig. 12 Current waveform of arc furnace
该波形为典型的尖顶波,可用三角波近似等效,等效三角波的占空比为 0.7。波形的正半周波峰值为2 900 A,正半周波均值为1 160 A,有效值为1 530 A。该波形对应两种检测方式的校准误差与近似三角波的校准误差值如表2所示,近似三角波与实际波形的校准误差相当。电弧炉电流峰值校准得到的有效值为2 048 A,均值校准得到的有效值为1 289 A。

表2 电弧炉电流波形的校准误差Table 2 Calibration error of arc furnace’s current waveform
由于电弧炉在熔化期电流值最大,而熔化期电流有效值为1 530 A,用于电流保护的断路器可以选择DW914(AH)-2000型号配电子脱扣器的低压断路器。在未考虑畸变电流下的脱扣校准误差时,断路器电子脱扣器的动作电流和动作时间整定值可按表3所示进行设置。
根据表3可知,过载长延时保护将在电流超过1.2Ir(即1 920 A)时动作。在电弧炉熔化最大电流值时,根据峰值检测校准得到的电流有效值为实际电流有效值的1.339倍(即2 048 A),已超过过载长延时保护的动作值,将会引起电子脱扣器误跳闸。这是因为电子脱扣器的峰值检测校准误差为正,即过高估计了线路电流,导致实际动作电流值小于整定值。此时,若考虑脱扣校准误差,按 1.339倍的负载额定电流来进行保护整定,即可避免脱扣器误跳闸。

表3 电弧炉用断路器电流保护整定值Table 3 Current protection setting values of circuit breaker for arc furnace
6 结论
本文将典型的非线性负荷电流波形简化为三角波和矩形波,利用峰值系数和波形系数这两个特征量,定量分析了采用峰值检测和均值检测的电子脱扣器的校准误差,得到了峰值检测校准误差曲线和均值检测校准误差曲线。对于三角波和矩形波而言,其波形系数、峰值系数以及电子脱扣器的脱扣校准误差仅与波形占空比α有关,且存在一一对应关系。而谐波畸变率(THD)和波形占空比α之间并非一一对应,所以通过 THD值来分析畸变波形下的脱扣校准误差具有误导性。总之,虽然电子脱扣器的校准误差是由波形电流畸变引起的,但却不能通过谐波畸变率来评估校准误差;而根据脱扣校准原理,从峰值系数和波形系数入手,可得到校准误差的精确表达式,以此可定量分析脱扣校准误差。
电子脱扣器的动作电流整定值允许在一定范围内自行调节,这样只要知道负载波形特征,就可以根据其校准误差曲线对动作电流整定值进行适当的调整,即可避免非线性负荷波形畸变造成的脱扣器误动作或拒动作现象。
[1] 陆俭国, 王景芹. 低压断路器可靠性评估方法与验证试验方案的研究[J]. 中国电机工程学报, 2004, 24(12): 193-197.
LU Jianguo, WANG Jingqin. Study on the reliability evaluation method and compliance test sampling plan of low-voltage circuit breaker[J]. Proceedings of the CSEE, 2004, 24(12): 193-197.
[2] IEEE Std 3004.5™-2014. IEEE recommended practice for the application of low-voltage circuit breakers in industrial and commercial power systems[S]. New York, USA: IEEE, 2014.
[3] 欧阳森, 刘平, 吴彤彤, 等. 低压脱扣器电压暂降敏感性试验研究[J]. 电网技术, 2015, 39(2): 575-581.
OUYANG Sen, LIU Ping, WU Tongtong, et al. Experimental research on sensitivity of low voltage releaser to voltage sag[J]. Power System Technology, 2015, 39(2): 575-581.
[4] 马宇辉, 吴文宣, 江道灼. 取消低压断路器欠压(失压)脱扣功能的危害及对策[J]. 继电器, 2007, 35(18): 71-74.
MA Yuhui, WU Wenxuan, JIANG Daozhuo. Damage brought by canceling the under-voltage (no-voltage) release of low-voltage breaker and its solutions[J]. Relay, 2007, 35(18): 71-74.
[5] 翟国富, 毕勇, 许峰, 等. 采用有限元法分析电网谐波对断路器动作特性的影响[J]. 中国电机工程学报, 2003, 23(1): 112-115.
ZHAI Guofu, BI Yong, XU Feng, et al. Power network harmonic’s effect on operational characteristic of circuit breaker with finite element analysis method[J]. Proceedings of the CSEE, 2003, 23(1): 112-115.
[6] 孙世双, 郑益慧, 张文荣, 等. 低压断路器智能控制装置可靠性研究[J]. 电力自动化设备, 2002, 22(7): 23-26.
SUN Shishuang, ZHENG Yihui, ZHANG Wenrong, et al. Investigation on reliability of intelligent trip device for LV circuit breakers[J]. Electric Power Automation Equipment, 2002, 22(7): 23-26.
[7] 吴晓峰, 张浩. 基于数字信号处理器的智能型断路器测控系统的研制[J]. 电网技术, 2003, 27(7): 70-74.
WU Xiaofeng, ZHANG Hao. Development of digital signal processor based measuring and controlling unit for intelligent breaker[J]. Power System Technology, 2003, 27(7): 70-74.
[8] FIDIGATTI A, RAGAINI E. Effect of harmonic pollution on low voltage overcurrent protection[C] // 14th International Conference on Harmonics and Quality of Power (ICHQP). [S.l.]: IEEE, 2010: 1-4.
[9] 唐轶, 陈奎, 谷露, 等. 一种高精度快速计算电力谐波参数的方法[J]. 电力系统保护与控制, 2013, 41(5): 43-47.
TANG Yi, CHEN Kui, GU Lu, et al. An accurate and fast approach to calculating the power harmonics parameters[J]. Power System Protection and Control, 2013, 41(5): 43-47.
[10] 彭祥华, 周群, 曹晓燕. 一种高精度的电网谐波/间谐波检测的组合优化算法[J]. 电力系统保护与控制, 2014, 42(23): 95-101.
PENG Xianghua, ZHOU Qun, CAO Xiaoyan. A high precision combinational optimization algorithm of power grid harmonic/inter-harmonic signal detection[J]. Power System Protection and Control, 2014, 42(23): 95-101.
[11] 陈欢, 何怡刚, 肖建平, 等. 基于CWT和DWT相结合的谐波检测[J]. 电力系统保护与控制, 2015, 43(20): 71-75.
CHEN Huan, HE Yigang, XIAO Jianping, et al. Harmonics detection based on a combination of continuous wavelet transform and discrete wavelet transform[J]. Power System Protection and Control, 2015, 43(20): 71-75.
[12] IEEE Std C37.17™-2012. IEEE standard for trip systems for low-voltage (1000 V and below) AC and general purpose (1500 V and below) DC power circuit breakers[S]. New York, USA: IEEE, 2012.
[13] DUGAN R C. 电力系统电能质量[M]. 林海雪, 肖湘宁,等, 译. 北京: 中国电力出版社, 2012.
[14] 郭继红, 颜湘武. 用于谐波分析研究的电弧炉系统的模型和仿真[J]. 继电器, 2005, 33(8): 31-37.
GUO Jihong, YAN Xiangwu. Model and simulation of arc furnace system for harmonic analysis[J]. Relay, 2005, 33(8): 31-37.
Calibration error analysis of electronic trip unit under distorted current
NIU Chunchun, ZHAO Lihua, FENG Zhengsong, NIU Shuaijie, FU Rongrong
(School of Electrical Engineering and Information, Sichuan University, Chengdu 610065, China)
Distorted current causes the electronic trip unit malfunction, which results in low-voltage circuit breaker’s tripping without fault. To analyze the effect of two typical distorted waveforms, triangular wave and square wave, on the electronic trip unit with different current detection and control methods, the peak coefficient KPand waveform coefficientKWare used. The defect that total harmonic distortion (THD) can’t be used to analyze the harmonic current impact on the electronic trip unit’s calibration error correctly and quantitatively is overcome. The calibration error can be seen accurately and intuitively through the calibration error curve of peak value detection and mean value detection. According to the nonlinear load’s waveform characteristic and calibration error curve, the frequent malfunction of electronic trip unit caused by distorted current can be avoided in a certain extent by adjusting the action current setting value properly.
electronic trip unit (ETU); distorted current; peak value detection; mean value detection; calibration error
2015-10-15;
2015-12-03
牛纯春(1991-),男,硕士研究生,研究方向为电力电子技术在电力系统中的应用、配电网电能质量;E-mail: chunke_1991@163.com
(编辑 周金梅)
10.7667/PSPC151818
赵莉华(1968-),女,硕士,副教授,研究方向为电力电子技术在电力系统中的应用、电能质量、有源电力滤波器等。E-mail: tyorika@163.com
