基于遗传优化的调控系统缺失数据填补算法

王一蓉，王瑞杰，陈文刚，吴润泽

基于遗传优化的调控系统缺失数据填补算法

王一蓉1，王瑞杰2，陈文刚3，吴润泽2

(1.北京国电通网络技术有限公司，北京 100070；2.华北电力大学电气与电子工程学院，北京102206; 3.国网山西省电力公司晋城供电公司，山西 晋城 048000)

数据缺失问题是电网调度控制系统中重要的研究课题。为保证数据的完整性和准确性，提出一种基于遗传优化的调度控制系统缺失数据填补算法。该算法利用遗传优化方法估计不完整数据的参数，获得最优数据参数，在最优参数基础上利用马尔科夫链蒙特卡罗算法对缺失数据进行估计、填补。对电力调度控制系统中缺失数据的填补结果分析，发现所提出的缺失数据填补算法能快速准确地填补缺失数据，保证了电网调度控制数据的完整性和准确性。

电网调度控制系统；缺失数据；遗传算法；最优参数；填补算法

0 引言

智能电网是未来电力系统的理想解决方案，而调度环节是智能电网的神经中枢。为了建设智能调度系统和电力系统可视化需要对海量的电力数据进行处理[1]。但是，电力数据中存在数据缺失问题。一方面，电网调度控制系统采集的数据中普遍存在数据畸形和缺失的问题，比如数据采集与监视控制系统、广域监测系统采集到畸形信号或者缺失数据[2-4]；另一方面，对调控领域的多源数据进行整合分析时，容易造成数据缺失问题[5]。随着大数据时代的到来，电网也逐步走向智能化，即智能电网。为了实现智能电网，必须获取海量的、真实完整的状态数据[6]。因此，为了保证电网业务数据的真实性、完整性、准确性，促进智能电网大数据的发展，需要对不完整的数据进行数据填充来解决缺失数据问题。

缺失数据的特征分为缺失数据模式和机制。缺失数据模式描述了以观测数据和缺失数据两部分。通常缺失数据模式分为两类：单调缺失模式和任意缺失模式。缺失数据机制反映了缺失数据与其他观测数据之间的相依关系。因此，在缺失数据填充中确定缺失机制非常重要。按照Little和Rubin提出的缺失机制方法，将其分为三类：完全随机缺失(Missing Completely at Random，MCAR)、随机缺失(Missing at Random，MAR)和非随机缺失(Missing not at Random，NMAR)[7]。对于MCRA机制，数据缺失是随机的，不依赖其他数据；对于MAR机制，数据的缺失只依赖已观测的部分，而不依赖于缺失的部分；对于NMAR机制，缺失数据不仅依赖于已观测的部分，还依赖于缺失的数据。根据缺失数据的模式机制，可以确定相应的缺失数据处理方法。目前存在一些不完整数据填充算法，主要包括基于属性重要性的填充算法、基于最大期望(Expectation Maximization, EM)算法和贝叶斯网络的丢失数据填充算法、演绎填补法、回归填补法、最近距离填补法，多重填补算法(Multiple Imputation, MI)[8-12]。实际情况中，NMAR机制的缺失数据最常见，对该机制的缺失数据进行数据填充时，多重填补算法的填充效果相对较好，其通过多个完整的数据集进行数据的统计分析，并将结果综合分析产生推断，反映了缺失数据带来的不确定性和增加了估计的效率。但是，MI中也存在技术挑战，在MI中用到EM算法进行数据参数估计，通过估计的参数对缺失数据进行估计。EM 算法估计不完整数据的参数时，采用极大似然估计法，计算似然函数的极值确定最优参数，其未考虑全部参数情况，因此，EM 算法估计的最优参数可能为局部最优参数，不准确的参数影响缺失数据的准确性。

为了提高多重填补算法估计缺失数据的准确性和加快算法的计算过程，本文在保持MI算法良好的填充性能上对其进行了改进，针对电力调度控制系统采集数据不完整的问题提出一种基于遗传算法的调度控制系统缺失数据填充算法。该算法以遗传算法思想对不完整数据的参数进行估计，需找数据参数的全局最优解，提高了参数值的准确度。在最优参数的基础上通过常用的马尔科夫蒙特卡洛链的方法进行缺失数据填补。本文以电网调度控制系统采集到的数据为实例，证明了本文算法能快速准确地填补缺失数据，保证了电网调度控制数据的完整性和准确性。

1 基于遗传优化的填补算法

本文中采用马尔科夫链蒙特卡罗(Markov Chain Monte Carlo，MCMC)方法对NMAR机制电力调度控制系统采集的缺失数据进行填充。该方法以不完整数据集和不完整数据的参数为条件，对缺失数据进行迭代估计。由于数据缺失无法确定数据集的参数，因此，对缺失数据填充之前需要对整个不完整数据的参数进行估计。而且，估计的参数与实际值越相近，估计的缺失数据越接近真实值。为了提高参数的有效性，本文采用基于遗传的算法对参数进行估计。

1.1 估计数据均值和协方差矩阵

在电力数据中，数据的分布主要分为两大类：正态分布和幂律分布。其中在对不完整数据参数进行估计时，本文以数据的对数似然函数作为目标函数建立估计模型，其中均值和方差矩阵作为参数。

本文以包含参数的对数似然函数作为目标函数，通过已有样本获得参数的相应约束条件，由目标函数和约束条件共同构成估计模型。其次，通过迭代的过程对参数值进行估计，而参数估计值的精确度是由目标函数确定。目标函数越大，所估计的参数越准确。因此，根据目标函数极大值所对应的参数确定最优参数。由此可得，估计数据均值和协方差矩阵的框架图，如图1所示。

图1 数据参数估计方框图Fig. 1 Block diagram for data parameter estimation

含有待估计的均值和协方差矩阵的对数似然函数为

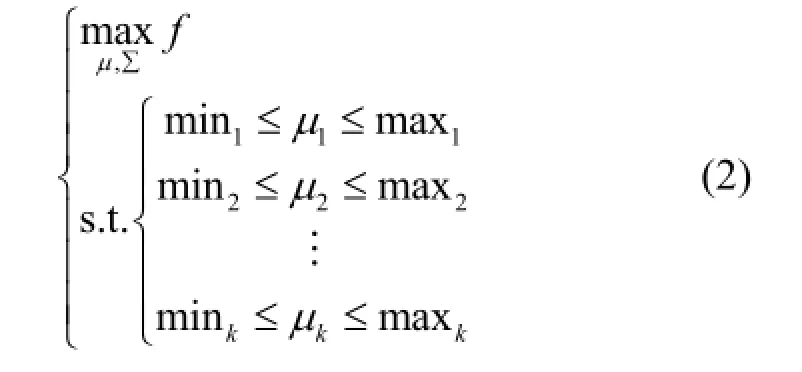
确定待估计参数和参数估计模型之后，要在约束条件内随机生成参数种群，种群的规模可以根据数据缺失率来定(当数据缺失率较高时，种群规模可以适当增大；反之，规模适当减小)。种群规模一般定为100。为了加快得到最优解的速度，第一代种群中需要包含数据集obsY 所对应的均值和协方差矩阵。种群中个体进行初始化后，需要有适应函数来计算每个参数个体在种群中的适应度，以确定个体的优劣程度。本文以目标函数作为适应函数。当函数值越大，参数越接近真实值、越准确。

种群迭代过程模拟了自然进化规律。根据计算得到的个体的适应度，对适应度高的部分个体，采取保留的措施；同时对参数个体，利用交叉、变异措施进行进化，实现得到更优的参数个体。在交叉、变异过程中，交叉概率 Pc和变异概率mP所对应的两个概率值将直接影响着种群的进化速度，而且一般是通过经验得到的。

其中，交叉进化过程如下：设 Pc为交叉概率，取值范围为，建议取0.8。参数种群中含有n个参数个体，从参数种群中选取cn P×个参数个体进行交叉操作。假设表示参数种群的父代，将其随机选择两个参数组成交叉对，记作且i j¹ 。以交叉对为例说明交叉操作的过程，从区间产生一个随机数e，在集合中随机选择v，按式(2)对中的进行交叉操作，产生两个后代，得到新的参数

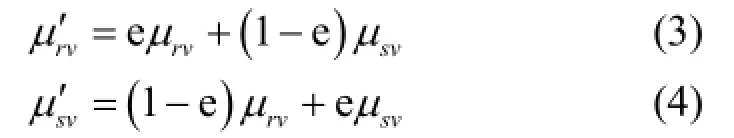
其变异进化过程如下：设mP为变异概率，取值范围为( )0,1，建议取0.06，参数种群中含有n个参数个体，从参数种群中选取mn P× 个参数个体进行交叉操作。设是参数种群中的个体，包含的均值为。取范围内的随机值，按式(4)进行变异，则变异后的均值为，则变异后的参数可记作'hq。

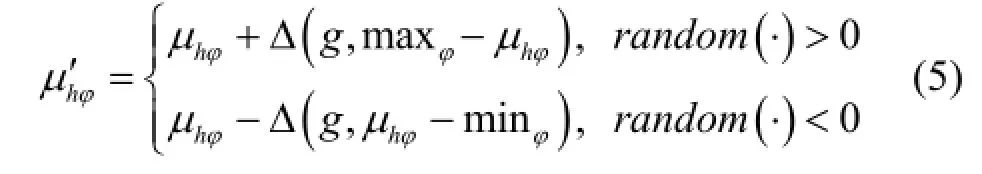
本文算法参数估计迭代终止条件为最优参数对应的适应函数值变化范围小于某个很小的值a，即，其中为迭代循环了i次后最优参数对应的目标函数值。当满足终止条件时，终止迭代，得到最优估计值。若满足则终止迭代，得到最优估计值；若不满足则返回继续迭代寻优。需要注意，取值范围为，建议取 10-4，因为取值过小，迭代次数就会大幅度的增加，增加了系统开销和迭代时间，但是目标函数值的变化幅度较小；a取值过大，确定的参数误差较大，未实现寻找最优参数个体的目的。

相对于EM算法估计参数，本文基于遗传算法进行不完整数据参数估计，扩大了待估计参数的范围，在求解数据参数问题中，容易跳出局部收敛情况，得到更优的解，具有更好的收敛性和收敛速度。

1.2 估计缺失数据

为了提高估计值的准确性，针对电力调度控制系统中以随机缺失模式为主的缺失数据，本文利用MCMC方法对缺失数据进行迭代估计。填补的过程如所述。

(1) 以1.1节估计的均值向量、协方差矩阵和数据集obsY 为条件，对每个缺失数据独立地估计，即从条件分布中，得出的值。

(2) 根据填补后的完整数据集，模拟数据的后验均值向量和协方差矩阵，即中得到，将其用在(1)中，重复进行。

(1)、(2)两步相互迭代对缺失数据进行填充，直到填补的缺失数据以及对应的数据参数不再变化或者变化范围在允许的范围之内。也就是说，在填补过程中产生一条马尔科夫链，该链会聚于分布。当该分布稳定时，将得到的misY 填补缺失数据，获得最终的完整数据集。

为了减小误差提高精确度，本文采用产生m (一般m取5)条马尔科夫链进行填补，填补之后会得到m个完整的数据集。当需要对原数据集进行统计分析时，需要首先对m个完整的数据集进行分析，之后将分析结果进行综合推断分析。

2 实例分析

为了分析本文所提出算法的性能，本文以电力调度控制系统中山西省某变电站数据为实例数据，利用不同算法对缺失数据填充过程和结果进行了仿真分析。该实例数据由8个变量的数据组成，其整体符合正态分布。为了准确地分析填补算法的性能，在选取完整数据基础上，人为地去掉部分数据之后作为实例数据。

本文将基于EM算法与本文算法估计数据参数的过程进行仿真比较。其中，在本文算法的参数估计过程中，将初始种群规模定为 200，交叉概率Pc=0.8，变异概率 Pm=0.06。通过两种算法分别估计缺失数据的均值和协方差矩阵，其中均值情况如表1所示。通过每个属性所对应的均值可以发现，本文算法估计的均值更接近于更准确。

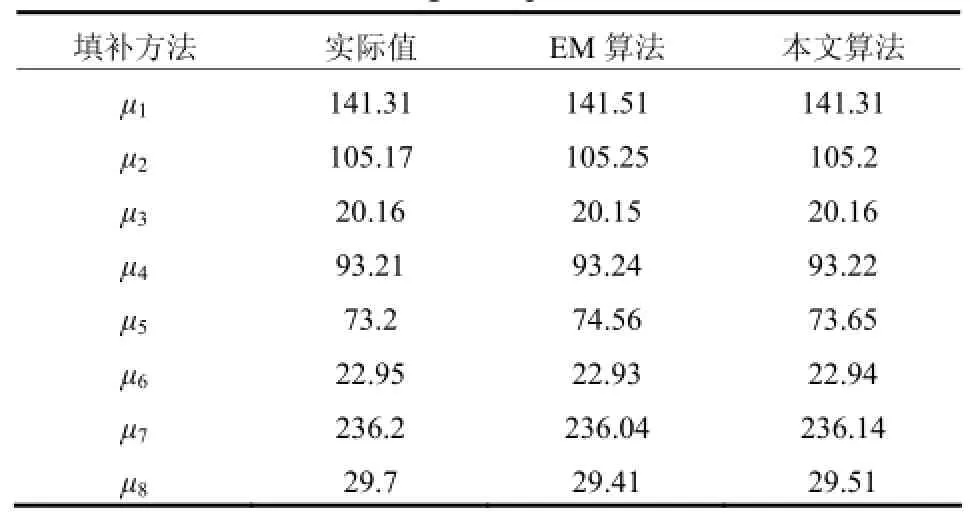
表1 真实数据参数与填补后参数比较Table 1 Comparative between real data parametersand filling data parameters

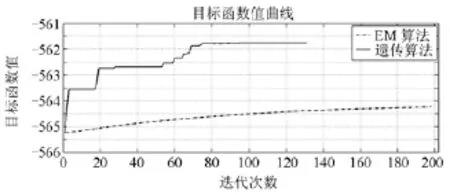
图2 EM算法与GA算法估计参数过程Fig. 2 Estimation parameters process using EM algorithm and GA algorithm

EM算法和GA算法估计参数迭代过程如图2所示。由图可知，EM 算法在计算目标函数最优解过程中产生了局部最优解，并且迭代的速度缓慢，共迭代了198次，而且每代与前一代之间目标函数值变化比较小。而GA算法在计算目标函数值时，容易跳出局部最优解，获得更优的参数。同时，该算法在迭代过程中，存在跳变的可能，大大加快了迭代的速度，本文中迭代次数为131次。

利用SAS软件实现MCMC缺失数据填充过程，本文马尔科夫链的数量m取5，即基于EM的MI算法和本文填充算法的填充结果分别为5个完整的数据集。同时，采用常用的均值填补法和最近邻域法对不完整数据进行填充。衡量填充数据精度的指标有3个：真值与估计值的平均偏差Bias，平均绝对偏差ABS和平均偏移均方根RMSD。设是估计值， Xi是模拟真值，m为缺失数据的个数。在中，为平均偏差 Bias，为平均绝对偏差ABS，后再对和式求算术平方根即RMSD。ABS、RMSD值越小，估计准确性越高。对同一缺失密度下的不完整数据，采用不同的算法进行填充，填充数据精度如表2所示。可得，4种算法中，本文算法和基于EM的MI算法得到的填充数据偏差较小，更接近真实数据，其中本文填补算法对应的填补数据准确性最高。

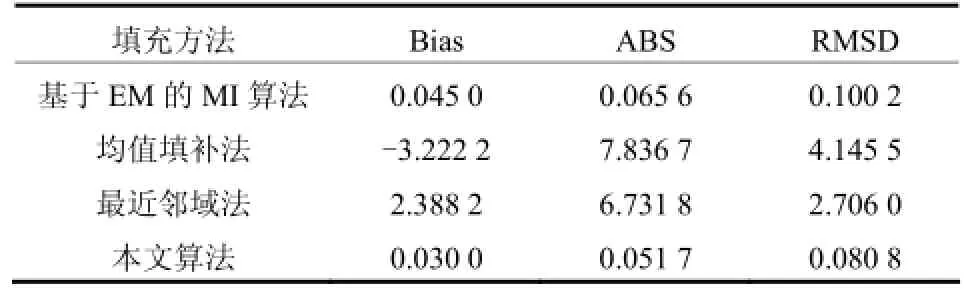
表2 不同算法的填充数据精度指标Table 2 Accuracy index of filling data by different algorithms

本文算法对数据集中数据缺失密度(数据中连续多个数据缺失情况)分别为 12.5%、25%、37.5%的缺失情况进行填充分析，如表3所示。可得，随着数据缺失密度的增大，填充数据偏差也增大。

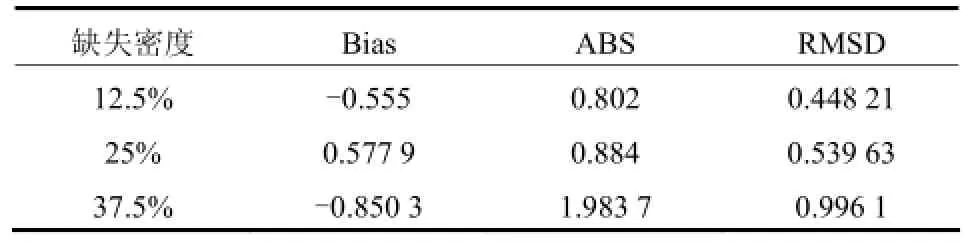
表3 不同缺失密度下的填充数据精度指标Table 3 Accuracy index of filling data under different loss density

3 结论

随着大数据时代的到来，对电力系统数据的质量要求也越来越高。然而，电力调度控制系统中普遍存在数据缺失的问题。部分数据的缺失影响了整体数据的完整性和真实性，干扰了数据后期的清洗、整合、挖掘等处理操作，造成数据分析、挖掘的结论与真实结论存在较大差异。近年来盛行的多重填充法是解决数据缺失的有效方法，而如今面对海量的数据需要加快算法迭代速度以及更准确的估计缺失值。本文提出一种基于遗传优化的调度控制系统缺失数据填补方法，不仅可加快估计不完整数据参数的迭代速度，而且有效地提高了缺失数据所估计值的准确度。

[1] 沈国辉, 孙丽卿, 游大宁, 等. 智能调度系统信息综合可视化方法[J]. 电力系统保护与控制, 2014, 42(13): 129-134.

SHEN Guohui, SUN Liqing, YOU Daning, et al. Intelligent dispatch system information comprehensive visualization method[J]. Power System Protection and Control, 2014, 42(13): 129-134.

[2] 高振兴, 郭创新, 俞斌, 等. 基于多源信息融合的电网故障诊断方法研究[J]. 电力系统保护与控制, 2011, 39(6): 17-23.

GAO Zhenxing, GUO Chuangxin, YU Bin, et al. Study of a fault diagnosis approach for power grid with information fusion based on multi-data resources[J]. Power System Protection and Control, 2011, 39(6): 17-23.

[3] 谢善益, 杨强, 梁成辉, 等. 输变电设备远程诊断信息平台中的统一状态监测模型研究[J]. 电力系统保护与控制, 2014, 42(11): 86-91.

XIE Shanyi, YANG Qiang, LIANG Chenghui, et al. Research of unified condition monitoring information model in data platform of power transmission equipment remote monitoring and diagnosis[J]. Power System Protection and Control, 2014, 42(11): 86-91.

[4] 程学珍, 陈强, 于永进, 等. 基于最大似然译码字的Petri网电网故障诊断方法[J]. 电工技术学报, 2015, 30(15): 46-52.

CHENG Xuezhen, CHEN Qiang, YU Yongjin, et al. A fault diagnosis approach of power networks based on maximum likelihood decoding Peteri net models[J]. Transactions of China Electrotechnical Society, 2015, 30(15): 46-52.

[5] 荀挺, 张珂珩, 薛浩然, 等. 电网调控数据综合智能分析决策架构设计[J]. 电力系统保护与控制, 2015, 43(11): 121-127.

XUN Ting, ZHANG Keheng, XUE Haoran, et al. Framework design of the analysis decision system about the power grid data[J]. Power System Protection and Control, 2015, 43(11): 121-127.

[6] 宋亚奇, 周国亮, 朱永利. 智能电网大数据处理技术现状与挑战[J]. 电网技术, 2013, 37(4): 927-935.

SONG Yaqi, ZHOU Guoliang, ZHU Yongli. Present status and challenges of big data processing in smart grid[J]. Power System Technology, 2013, 37(4): 927-935.

[7] AZARKHAIL M, PETER W. Uncertainty management in model-based imputation for missing data[C] // Reliability and Maintainability Symposium (RAMS), 2013 Proceedings-Annual: IEEE, 2013: 1-7.

[8] 陈志奎, 吕爱玲, 张清辰. 基于属性重要性的不完备数据填充算法[J]. 微电子学与计算机, 2013, 30(7): 167-176.

CHEN Zhikui, LÜ Ailing, ZHANG Qingchen. A new algorithm for imputing missing data based on distinguishing the importance of attributes[J]. Microelectronics & Computer, 2013, 30(7): 167-176.

[9] ZHU Xiaofeng, ZHANG Shichao. Missing value estimation for mixed-attribute data set[J]. IEEE Transactions on Knowledge and Data Engineering, 2011, 23(1): 110-121.

[10] ENDERS C K. Applied missing data analysis[M]. United States: The Guilford Press, 2010: 22-50.

[11] LITTLE R J A, RUBIN D B. Statistical analysis with missing data[M]. United States: John Wiley & Sons, Inc., 2002: 127-169.

[12] 史峰, 王辉, 胡斐, 等. MATLAB智能算法30个案例分析[M]. 北京: 北京航空航天大学出版社, 2011.

(编辑 周金梅)

A missing data filling algorithm for dispatching and control system based on genetic optimization

WANG Yirong1, WANG Ruijie2, CHEN Wengang3, WU Runze2
(1. Beijing GuoDianTong Network Technology Company Limited, Beijing 100070, China; 2. School of Electrical & Electronic Engineering, North China Electric Power University, Beijing 102206, China; 3. Jincheng Branch of Shanxi Power Corporation under State Grid, Jincheng 048000, China)

The problem of data loss is an important research topic in the grid dispatching and control system. A new method based on genetic optimization for dealing with missing data is proposed to ensure the data integrity and accuracy. The proposed method can estimate incomplete data parameters by genetic optimization algorithm. According to the optimal parameters, the Markov Chain Monte Carlo algorithm is used to estimate the missing data. Through filling the incomplete data in the grid dispatching and control system, it is discovered that the proposed method can find more missing data within the same time duration and improve the accuracy of estimated values which guarantee the data integrity and accuracy.

grid dispatching and control system; missing data; genetic optimization method; optimal parameters; filling algorithm

2015-10-22；

2015-12-21

王一蓉(1979-)，女，高级工程师，研究方向为电力系统信息通信技术；E-mail: wangyirong@sgitg.sgcc.com.cn

王瑞杰(1991-)，男，通信作者，硕士研究生，研究方向为电力数据处理及信息化建设；E-mail: wang_ruijie2015@ 163.com

陈文刚(1971-)，男，高级工程师，研究方向为自动化维护及网络管理。E-mail: jcchenwangang@163.com

10.7667/PSPC151867