含VSC-HVDC并网风电场的电力系统最优潮流计算
2016-04-12杨智豪牟龙华
杨智豪,牟龙华,刘 仲
含VSC-HVDC并网风电场的电力系统最优潮流计算
杨智豪,牟龙华,刘 仲
(同济大学电气工程系,上海 201804)
由于风电场出力的实际值通常在预测值附近随机波动,所以在潮流计算时还应考虑风电场出力的随机性。针对风电场通过VSC-HVDC并网的情形,为了使电网既能安全运行,又能实现经济调度,提出了一种基于场景分析的最优潮流计算模型。模型以火电机组的总成本最小为目标函数,并考虑火电机组在预测场景和误差场景有功出力的调节范围约束,采用内点法进行求解。算例结果表明,引入误差场景后,虽然火电机组的总成本增加了,但是风电场出力的随机性对火电机组快速调节出力能力的要求得到了满足,从而保障了电网的安全运行。
风电场;VSC-HVDC;交直流系统;最优潮流;内点法;场景法
0 引言
在环境污染日益严峻的社会背景下,可再生能源的使用已经受到人们的重视。随着可再生能源发电和高压直流输电的发展,可再生能源发电的并网技术也越来越成熟[1-4]。现有的风电场的并网方式主要有三类:通过交流线路并网;通过传统HVDC线路并网;通过VSC-HVDC线路并网。其中VSC- HVDC输电技术拥有的众多优点使其成为了风电场并网连接方式的首选[5-6]。
对VSC-HVDC在电网运行中的稳态特性和控制方式进行分析是以VSC-HVDC的交直流系统潮流计算为前提条件的,这也是研究其暂态特性及安全运行方案的基础。因此,研究含VSC-HVDC的交直流系统潮流计算具有重要意义。文献[7]研究了VSC-HVDC的稳态功率特性,结合其控制方式的分析,建立了可用于牛顿−拉夫逊潮流计算方法的VSC-HVDC数学模型,解决了在使用交替求解法对含VSC-HVDC的交直流系统进行潮流计算时存在的问题,但在交直流耦合性很强时,交替求解法收敛性较差。文献[8]研究了电压源型换流器的多端直流输电系统的稳态模型,分析了统一迭代求解法与交替迭代求解法固有的缺陷,改进了交替迭代求解法使其可以应用于多端直流输电系统的潮流计算,但改进的交替迭代求解法迭代次数明显变多了。文献[9]提出了一种适用于牛顿法解最优潮流的VSC- HVDC模型,但由于牛顿法有效束集难以确定,所以较难用编程实现。文献[10]建立了一种适用于解最优潮流计算的VSC-HVDC稳态模型,并用原对偶内点法和预测校正内点法来计算该模型的最优潮流,但预测校正内点法在迭代时易出现校正方向错误,收敛性会变差。文献[11]提出了一种基于VSC-HVDC的风电场并网系统潮流解耦算法,但潮流计算中并未考虑风电场出力的随机性。
本文围绕风电场通过VSC-HVDC并网的潮流问题,重点研究了考虑风电场出力随机性时的最优潮流计算,提出了一种基于场景分析的最优潮流计算模型。模型以火电机组的总成本最小为目标函数,将风电场出力预测值定义为预测场景,将考虑风电场出力预测误差所生成的场景定义为误差场景,引入了火电机组在预测场景和误差场景有功出力的调节范围约束,以可能出现的风电出力场景模拟风电场出力的随机性,从而定量地描述出风电场出力的概率分布特性,确保了在火电机组有功出力快速调节范围内,可以快速调节火电机组的出力来适应风电场出力的波动,使电网运行的安全性和经济性实现较好的平衡协调。模型采用内点法进行求解,并通过算例验证了该模型的有效性。
1 含VSC-HVDC的交直流系统
1.1 VSC-HVDC稳态模型

图1 VSC-HVDC稳态模型
对于采用正弦波脉宽调制的两端VSC-HVDC输电系统,根据图1所示的参考方向,通过推导可以得到其稳态运行时的潮流计算方程[8]为
在式(1)~式(4)中,di、di、、M、si和si为单个VSC的6个直流状态变量。这6个基本变量中,只须知道其中两个就可算得另外4个,这已知的两个变量就是VSC的控制变量。
1.2 VSC-HVDC用于风电场并网时的控制方式分析
当VSC-HVDC连接有源交流网络时,VSC的控制方式有以下四种[12]:1) 定直流电压d和定无功功率s控制;2) 定直流电压d和定交流电压s控制;3) 定有功功率s和定无功功率s控制;4)定有功功率s和定交流电压s控制。
当风电场使用VSC-HVDC并网时,为了使输送端能够跟随风电场出力的变化相应地快速调节以满足全部接纳风电场出力,从而可以将风电场出力全部输送出去,因此风电场侧的VSC应该采用定有功功率控制方式。同时为了能够向风电场提供足够的无功功率以保证可以维持风电场机组机端电压的稳定,风电场侧的VSC还应该采用定无功功率控制方式。因此,风电场侧的VSC应该采用定有功功率和定无功功率的控制方式。
为了使VSC-HVDC系统两侧能够实现有功功率平衡,交流电网侧的VSC应该采用定直流电压的控制方式。此外,为了能够向交流侧电网迅速提供无功功率以维持交流电网电压稳定,交流侧电网换流站还应该采用定无功功率控制。因此,交流电网侧的VSC应该采用定直流电压和定无功功率的控制方式。
2 风电场经VSC-HVDC并网最优潮流模型
2.1 模型分析
风电场通过VSC-HVDC并网的交直流电力系统最优潮流模型可表示为
式中:为系统的控制量和状态量,=[G,G,,,di,di,,M,si,si],G和G分别为交流系统发电机的有功出力和无功出力,和分别为交流系统母线电压的幅值和相角,di,di,,M,si和si为VSC-HVDC系统的控制量与状态量;()为等式约束;()为不等式约束;和分别为()的下限和上限。
2.1.1目标函数
该模型的目标函数()为所有火力发电厂机组燃料费用的总和,如式(6)。
式中:G为火力发电机总数;2i、1i、0i为火力发电机的耗量特性曲线系数。
2.1.2 等式约束
等式约束()为各节点的功率平衡方程和式(1)~式(4)的VSC-HVDC系统的潮流计算方程。
若节点是和VSC-HVDC线路无关联的节点,其功率平衡方程和纯交流系统相同[13],如式(7)、式(8)。
式(7)和式(8)中:Δri和Δri分别为和VSC-HVDC线路无关联的节点功率不平衡量;和分别是和VSC-HVDC线路无关联的节点发出的有功功率和无功功率;ri是和VSC-HVDC线路无关联的节点的电压幅值;下标表示与节点直接相连的节点,用∈表示;U是节点的电压幅值;是节点、之间的电压相角差;G和B是节点、之间的电导和电纳。
若节点是和VSC-HVDC线路相关联的节点,其功率平衡方程如式(9)、式(10)。
式(9)和式(10)中:Δti和Δti分别为和VSC-HVDC线路相关联的节点功率不平衡量;和分别是和VSC-HVDC线路相关联的节点发出的有功功率和无功功率;ti是和VSC-HVDC线路相关联的节点的电压幅值;si和si分别是交流系统流入VSC的有功功率和无功功率。
2.1.3不等式约束
不等式约束()包括交流系统的发电机有功和无功出力约束,母线电压幅值上下限约束,支路有功潮流约束,如式(11);还包括每个VSC-HVDC线路基本变量的di、di、、M、si、si上下限约束,如式(12)。
2.2 风电场的场景策略
风电场与传统的系统电源并不相同,其出力受风能分布和风速变化等因素影响而具有随机性,使得风电场出力的预测难以精准。如果在最优潮流计算中不考虑风电场出力的随机性,将可能会造成火电机组无法快速调节出力来适应风电场出力的波动,最优解在实际运行中无法实施,有时甚至会威胁到系统的安全稳定运行。这就要求在含风电场的最优潮流中必须计及这种不确定因素的影响。
场景分析是解决风电场出力随机性的一种有效方法。场景分析的本质是用较易求解的多个确定性场景来描述难以用数学模型表示的不确定性因素,避免建立复杂的随机性模型,降低求解模型的难度。
本文采用场景分析的方法来处理风电场发电功率的随机性。场景划分仅考虑风电场出力的随机性,以可能出现的风电场出力场景模拟风电场出力的随机性。将风电场出力预测值定义为预测场景,将考虑风电场出力预测误差所生成的场景定义为误差场景。在考虑风电场出力的随机性时,如果研究的时间段较短,可以假设风速服从正态分布[14]。在近似计算时,可以认为风速和风电场出力呈线性关系,所以也可以假设风电场出力d服从正态分布,即
式中:为风电场出力预测值;为标准差。
目前的风电场出力预测误差在25%~40%[14],本文取风电场出力预测误差为其数学期望的±30%。误差场景的风电场出力将由服从正态分布的随机函数给出。
假设电网系统内有个火电机组,当增加个误差场景时,变量、等式约束和不等式约束都相应地增加倍,此外不等式约束还将增加×个火电机组有功出力快速调节范围的不等式约束,如式(14)。
式中:上标0表示预测场景,上标表示第个误差场景;下标表示第个火电机组;ΔGj为第个火电机组有功出力的快速调节范围。在引入误差场景后,按预测场景对应的最优解进行调度,即便风电场出力的实际值为各误差场景的风电场出力值,依然可以快速调节火电机组的出力来平衡风电场出力的预测误差,同时兼顾了电网运行的安全性和经济性。本文假设各火电机组有功出力所能满足的快速调节范围为其额定发电功率的±5%。
3 模型求解
含VSC-HVDC风电场并网的电力系统最优潮流问题在数学上其实是一个带约束条件的非线性规划问题,可采用内点法进行求解。
内点法的基本思路是:引入松弛变量将不等式约束转化为等式约束,然后用障碍函数法对松弛变量进行约束,把目标函数改造为障碍函数。这样便把含不等式约束的优化问题变成只含等式约束的优化问题,可用拉格朗日乘子法求解,构造的拉格朗日函数如式(15)。
式中:=[1,,y],=[1,,z],=[1,,w]均为拉格朗日乘子;=[1,,l]T,=[1,,u]T为松弛变量;为障碍常数。该模型的最优解须满足Karush-Kuhn-Tucker条件:
式中:=diag(1,,l);=diag(1,,u);=diag (1,,z);=diag(1,,w);=[1,, 1]T。
由式(20)和式(21)可以解得=(T-T)/(2),定义对偶间隙ap=T-T,则可以得到=ap/(2)。
但为了能有较好的收敛性,一般采用:
式中,∈(0,1)称为中心参数,一般取0.1,在大多数情况能有较好的收敛效果。
通过采用牛顿法对非线性方程组式(16)~式(21)进行求解,便可解得风电场经VSC-HVDC并网的交直流电力系统最优潮流模型式(5)的近似最优解。
4 算例分析
4.1 5机13节点交直流系统
以4机11节点纯交流电网[15]为例,在引入风电场及VSC-HVDC直流线路后修改为5机13节点交直流系统如图2。风电场接入13节点,假定风电场出力的预测值为6p.u.,并且风电场处有足够的无功补偿,使其维持电压稳定,因此可将其作为一个PV节点来处理[16],风电场出力经升压变压器后连接到VSC-HVDC线路,VSC-HVDC连接9和12节点。经过修改后,交直流系统中交流网络的参数仍然保持与原先纯交流电网相同,直流网络的参数如表1所示。各发电机出力上下限和费用函数[17]见表2,节点电压的上下限为1.06 p.u.和0.94 p.u.,升压变支路有功潮流上下限为9 p.u.和-9 p.u.,交流线路有功潮流上下限为16 p.u.和-16 p.u.。直流线路各变量的上下限见表3。
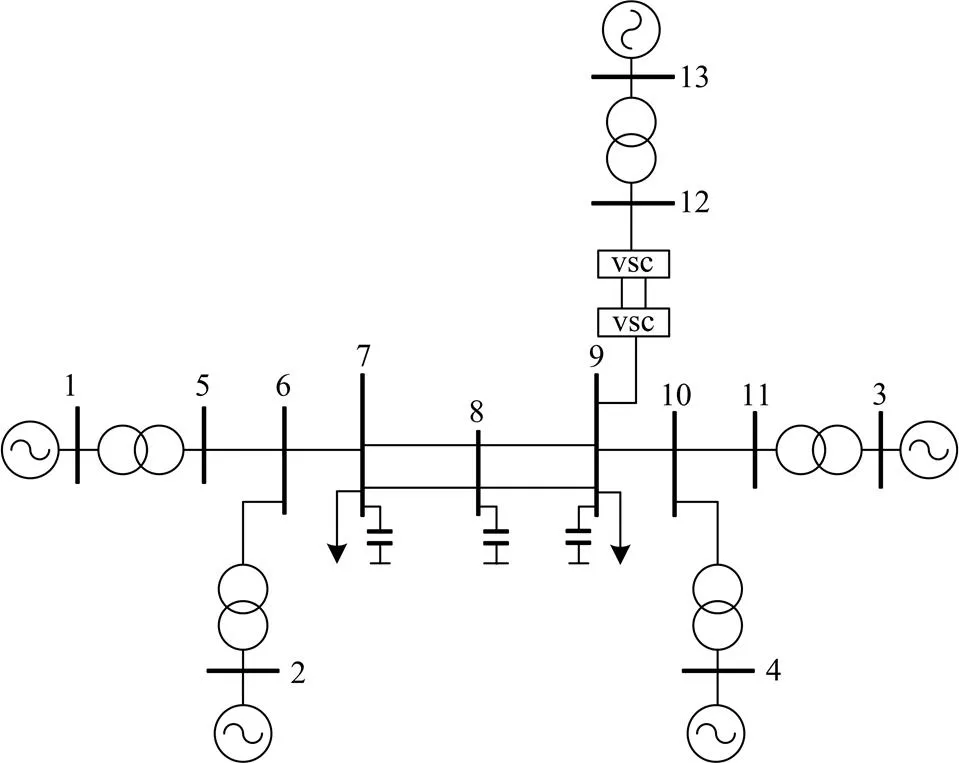
图2经修改的11节点交直流系统
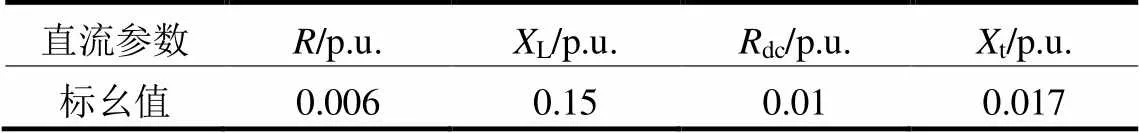
表1 VSC-HVDC线路参数
表1中,为换流器总损耗等效电阻;L为换流变压器阻抗;dc为直流线路电阻;t为12和13节点间升压变压器的电抗。同时,假定VSC-HVDC两侧的VSC参数相同。

表2 各火力发电机组的运行费用函数
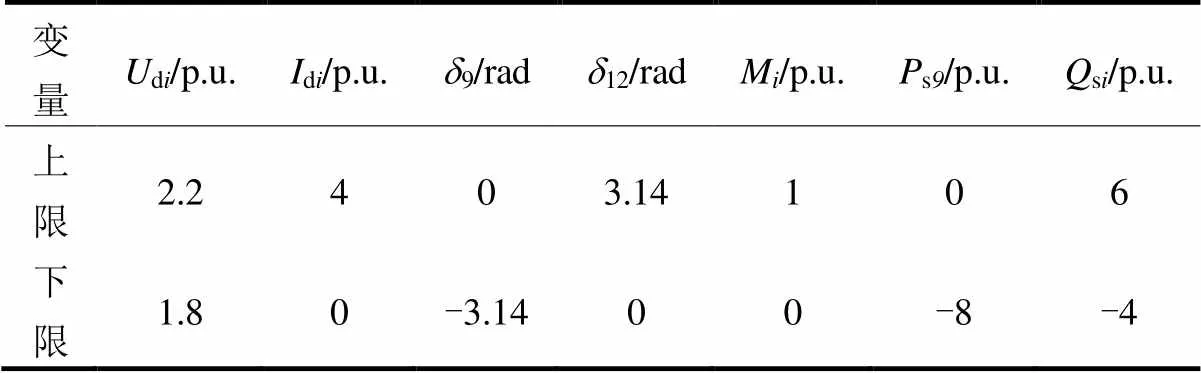
表3 直流变量的上下限
4.2 含误差场景的最优潮流计算
风电场通过VSC-HVDC并网的单个预测场景最优潮流,含5个误差场景最优潮流和含10个误差场景最优潮流的计算结果如表4所示。内点法的收敛判据是最大潮流偏差小于10-3且对偶间隙小于10-6。其中,5个误差场景的风电场出力分别为4.7 p.u.,5.6 p.u.,6.8 p.u.,7.1 p.u.,5.3 p.u.。10个误差场景的风电场出力分别为4.7 p.u.,5.6 p.u.,6.8 p.u.,7.1 p.u.,5.3 p.u.,6.7 p.u.,4.6 p.u.,5.3 p.u.,6.9 p.u.,6.2 p.u.。
从表4的计算结果分析可知,随着引入的误差场景越多,计算的工作量也越大,迭代次数增加。引入10个误差场景最优潮流的火电机组总成本最高,其次是引入5个误差场景,最后是单个预测场景。这是因为在引入误差场景后,约束条件变多,使得可行域有可能减小或者不变,最优解也就可能没有引入误差场景前那么好,所以火电机组的总成本可能会变大或者不变。引入误差场景后,虽然火电厂发电总成本增加了,但是确保了在火电机组有功出力快速调节范围内,可以快速调节火电机组的出力来适应风电场出力的波动,有效地解决风电场出力的随机性,电网因此可以更加安全地运行。这也从侧面体现了电网运行的安全性与经济性在很多时候是存在矛盾的,有时为了提高安全性需要牺牲一些经济性。
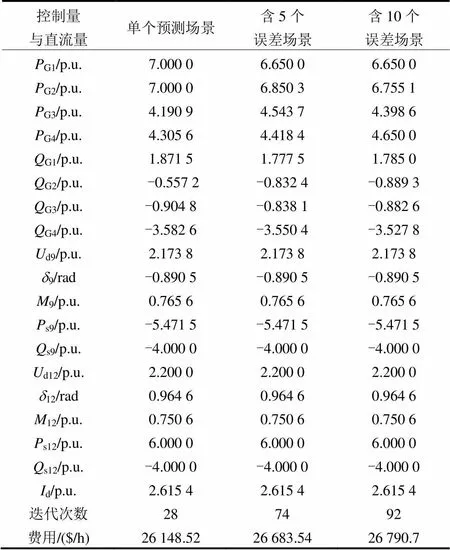
表4 最优潮流计算结果
5 结语
针对风电场通过VSC-HVDC并网的情形,本文建立了一种基于场景分析的最优潮流计算模型。模型以火电机组的总成本最小为目标函数,并考虑火电机组在预测场景和误差场景有功出力的调节范围约束,采用内点法进行求解。通过单个预测场景最优潮流计算结果,含5个误差场景最优潮流计算结果和含10个误差场景最优潮流计算结果的比较表明,在引入了误差场景后,虽然火电机组的总成本增加了,但是确保了在火电机组有功出力快速调节范围内,可以快速调节火电机组的出力来适应风电场出力的波动,从而保障电网安全运行。
[1] 文劲宇, 陈霞, 姚美齐, 等. 适用于海上风场并网的混合多端直流输电技术研究[J]. 电力系统保护与控制, 2013, 41(2): 55-61.
WEN Jinyu, CHEN Xia, YAO Meiqi, et al. Offshore wind power integration using hybrid multi-terminal HVDC technology[J]. Power System Protection and Control, 2013, 41(2): 55-61.
[2] 姚致清, 于飞, 赵倩, 等. 基于模块化多电平换流器的大型光伏并网系统仿真研究[J]. 中国电机工程学报, 2013, 33(36): 27-33.
YAO Zhiqing, YU Fei, ZHAO Qian, et al. Simulation research on large-scale PV grid-connected systems based on MMC[J]. Proceedings of the CSEE, 2013, 33(36): 27-33.
[3] 姚致清, 赵倩, 刘喜梅. 基于准同步原理的逆变器并网技术研究[J]. 电力系统保护与控制, 2011, 39(24): 123-126, 131.
YAO Zhiqing, ZHAO Qian, LIU Ximei. Research on grid-connected technology of inverter based on quasi synchronous principle[J]. Power System Protection and Control, 2011, 39(24): 123-126, 131.
[4] 黄晟, 王辉, 廖武, 等. 基于VSC-HVDC海上串联拓扑风电场低电压穿越控制策略研究[J]. 电工技术学报, 2015, 30(14): 362-369.
HUANG Sheng, WANG Hui, LIAO Wu, et al. Control strategy based on VSC-HVDC series topology offshore wind farm for low voltage ride through[J]. Transactions of China Electrotechnical Society, 2015, 30(14): 362-369.
[5] MITRA P, ZHANG Lidong, HARNEFORS L. Offshore wind integration to a weak grid by VSC-HVDC links using power-synchronization control: a case study[J]. IEEE Transactions on Power Delivery, 2014, 29(1): 453-461.
[6] 钱甜甜, 苗世洪, 白浩, 等. VSC-HVDC系统的离散滑模控制[J]. 电工技术学报, 2015, 30(13): 108-116.
QIAN Tiantian, MIAO Shihong, BAI Hao, et al. Discrete sliding mode control of VSC-HVDC system[J]. Transactions of China Electrotechnical Society, 2015, 30(13): 108-116.
[7] 郑超, 周孝信, 李若梅, 等. VSC-HVDC稳态特性与潮流算法的研究[J]. 中国电机工程学报, 2005, 25(6): 1-5.
ZHENG Chao, ZHOU Xiaoxin, LI Ruomei, et al. Study on the steady characteristics and algorithm of power flow for VSC-HVDC[J]. Proceedings of the CSEE, 2005, 25(6): 1-5.
[8] 叶芳, 卫志农, 孙国强. 含VSC-MTDC的交直流混合系统的改进潮流算法[J]. 河海大学学报(自然科学版), 2011, 39(3): 338-343.
YE Fang, WEI Zhinong, SUN Guoqiang. Modified power flow algorithm for hybrid AC-DC systems equipped with VSC-MTDC[J]. Journal of Hohai University (Natural Sciences), 2011, 39(3): 338-343.
[9] PIZANO-MARTINEZ A, FUERTE-ESQUIVEL C R, AMBRIZ-PÉREZ H, et al. Modeling of VSC-based HVDC systems for a Newton-Raphson OPF algorithm[J]. IEEE Transactions on Power Systems, 2007, 22(4): 1794-1803.
[10] 卫志农, 季聪, 孙国强, 等. 含VSC-HVDC的交直流系统内点法最优潮流计算[J]. 中国电机工程学报, 2012, 32(19): 89-95.
WEI Zhinong, JI Cong, SUN Guoqiang, et al. Interior-point optimal power flow of AC-DC system with VSC-HVDC[J]. Proceedings of the CSEE, 2012, 32(19): 89-95.
[11] 牛博彦, 胡林献, 张众. 基于VSC-HVDC的风电场并网系统潮流算法研究[J]. 电力系统保护与控制, 2014, 42(24): 6-11.
NIU Boyan, HU Linxian, ZHANG Zhong. Research on power flow of wind farm grid-connected system based on VSC-HVDC[J]. Power System Protection and Control, 2014, 42(24): 6-11.
[12] 姜燕. 基于VSC-HVDC并网风电场的暂态电压稳定性研究[D]. 北京: 华北电力大学, 2009.
JIANG Yan. Research on transient voltage stability of grid-connected wind farms based on VSC-HVDC[D]. Beijing: North China Electric Power University, 2009.
[13] 王锡凡, 方万良, 杜正春. 现代电力系统分析[M]. 北京: 科学出版社, 2003.
[14] 江岳文, 陈冲, 温步瀛.含风电场的电力系统机组组合问题随机模拟粒子群算法[J]. 电工技术学报, 2009, 24(6): 129-136.
JIANG Yuewen, CHEN Chong, WEN Buying. Particle swarm research of stochastic simulation for unit commitment in wind farms integrated power system[J]. Transactions of China Electrotechnical Society, 2009, 24(6): 129-136.
[15] 徐政. 交直流电力系统动态行为分析[M]. 北京: 机械工业出版社, 2005.
[16] 张元, 郝丽丽, 戴嘉祺. 风电场等值建模研究综述[J]. 电力系统保护与控制, 2015, 43(6): 138-146.
ZHANG Yuan, HAO Lili, DAI Jiaqi. Overview of the equivalent model research for wind farms[J]. Power System Protection and Control, 2015, 43(6): 138-146.
[17] 林舜江, 刘明波, 刘志文. 计及离散控制的交直流电力系统最优潮流计算[J]. 华南理工大学学报 (自然科学版), 2010, 38(10): 146-152.
LIN Shunjiang, LIU Mingbo, LIU Zhiwen. Optimal power flow calculation incorporating discrete controls in AC/DC power systems[J]. Journal of South China University of Technology (Natural Science Edition), 2010, 38(10): 146-152.
(编辑 魏小丽)
Optimal power flow of wind farm grid-connected system based on VSC-HVDC
YANG Zhihao, MU Longhua, LIU Zhong
(Department of Electrical Engineering, Tongji University, Shanghai 201804, China)
The actual value of wind power output varies randomly around the predicted value, thus, the randomness of wind power output should be considered in the power flow calculation. This paper proposes an optimal power flow calculation model based on scenario analysis of the wind farm connected to AC grid by VSC-HVDC, which can achieve secure operations and economic dispatch. The minimum total cost of thermal power plants is taken as the objective function of the model, and the adjusting range of active power output of thermal power plants under the forecasted wind power scenario and sampling scenarios is considered as constraints. Afterwards, the model is solved by utilizing interior point method. The calculation results show that, although the total cost of thermal power plants is increased after introducing sampling scenarios, the requirement of the capability of thermal power plants that can quickly adjust the randomness of wind power output is satisfied, thereby, the safety of grid operation is guaranteed.
wind farm; VSC-HVDC; AC-DC power system; optimal power flow (OPF); interior point method; scenario method
10.7667/PSPC151253
2015-07-20;
2015-10-22
杨智豪(1991-),男,硕士研究生,研究方向为分布式发电与微电网;E-mail: 1433130@tongji.edu.cn
牟龙华(1963-),男,教授,博士生导师,研究方向为电力系统继电保护、分布式发电与微电网、电能质量;E-mail: lhmu@tongji.edu.cn
刘 仲(1991-),男,硕士研究生,研究方向为微电网黑启动、微电网保护。E-mail: zeakyleo@163.com
