基于多精英协同进化单亲遗传算法的光伏电站功率汇集系统多目标分层优化
2016-04-12陈云超李兴源张祥成温生毅
陈云超,李兴源,苗 淼,张祥成,温生毅,成 静,王 曦
基于多精英协同进化单亲遗传算法的光伏电站功率汇集系统多目标分层优化
陈云超1,李兴源1,苗 淼1,张祥成2,温生毅3,成 静3,王 曦1
(1.四川大学电气信息学院,四川 成都 610065;2.青海省光伏发电并网技术重点实验室,青海 西宁 810008;3.国网青海省电力公司经济技术研究院,青海 西宁 810008)
针对大型光伏电站功率汇集外送拓扑设计问题,提出一种基于多精英协同进化单亲遗传算法(MCPGA)的多目标分层优化设计方法。首先深入阐述大型光伏电站功率汇集系统的构成,建立详细的数学优化模型。其次采用所提出的多精英协同进化单亲遗传算法进行拓扑结构优化设计,运用蒙特卡罗法进行可靠性分析。将经济性和可靠性指标作为汇集系统拓扑结构优化设计的评定指标。最后通过一算例仿真验证,所提方法是有效和实用的,算法收敛速度较快,从而为大型光伏电站汇集拓扑规划提供了有效的优化设计方法。
光伏电站;功率汇集;单亲遗传算法;经济性优化;可靠性分析
0 引言
随着日益严峻的能源危机和环境问题,提高能源利用率、开发新能源成为目前解决经济社会发展过程中能源短缺和环境污染问题的必然选择。近年来,光伏发电技术日趋成熟,发电效率及可靠性均得到明显提高,并网光伏发单已成为发展和研究热点[1-6]。
由于光伏电站内部电气设备众多,不同发电单元之间连接方式差异较大。而不同形式的汇集拓扑在经济性和可靠性上存在较大差异,并影响光伏电站的投资收益。因此设计经济合理而可靠性较高的汇集方案对并网光伏电站的经济、安全和稳定运行具有重要意义。
目前针对该方面的研究较少,且在光伏电站设计方面尚缺乏一套科学的理论指导,对新的拓扑结构的评价缺乏相应经济性、可靠性评估指标,无法全面的评估光伏电站优化设计[7]。文献[8]从工程设计的角度,对并网光伏电站太阳能电池方阵中的逆变器从容量、经济性和转换效率方面进行选择;从直流损耗和投资方面确定方阵装机容量。文献[9]讨论了光伏电站内部发电单元之间、发电单元与升压站间、升压站主接线和站用电接线方式,对接线方案分别从经济和技术方面进行比较分析,但并未从发电单元之间进行详细优化布局设计。
本文提出一种基于多精英协同进化单亲遗传算法的多目标分层设计方法,借鉴多旅行商问题求解思路,以投资成本作为经济指标,以等效容量作为可靠性指标,二者共同作为汇集系统拓扑结构设计评估指标。运用自下而上分层设计思想,先进行光伏电站内部集电系统拓扑设计,再进行外部传输系统设计,最终完成大型光伏电站功率汇集系统拓扑设计。
1 并网光伏电站电气系统构成
目前国内所建光伏电站通常将光伏阵列、汇流器和逆变器相连,而并网逆变器容量一般选择为0.5 MW,由于逆变器出口电压相对较低,如若直接将逆变器与升压变电站相连,则电能损耗较大。故通常将两个0.5 MW的逆变器并列后与双分裂变压器的低压侧相连接,共同构成1 MW的光伏发电单元[10],如图1所示。
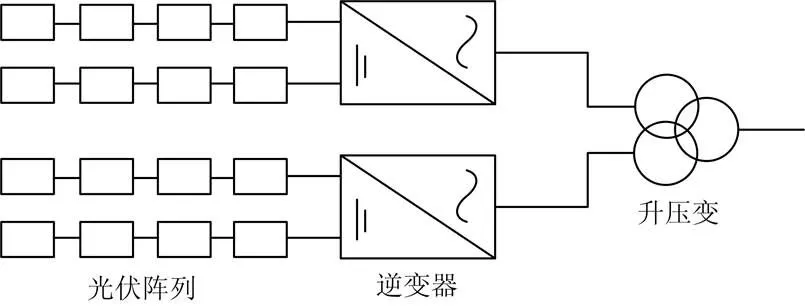
图1光伏发电单元
并网光伏电站功率汇集系统由光伏电站内部集电系统和外部输电系统两部分构成。其中内部集电系统由多个光伏发电单元通过汇集电缆采用不同连接方式汇集后送入中心变电站,而传输系统则由中心变电站、终端变电站和传输导线构成,如图2所示。
2 光伏电站汇集系统多目标分层优化策略
2.1基于多精英协同进化单亲遗传算法的经济性优化
2.1.1数学模型
由上述分析可知,功率汇集系统投资成本取决于:1) 光伏发电单元数目及位置分布;2) 中心变电站的数量及其位置分布;3) 系统连接方式以及汇集导线型号和长度。

图2光伏汇集系统构成
本文主要针对光伏电站内部集电系统以及传输系统之间的拓扑连接方式进行优化,以经济性和可靠性指标作为拓扑结构优化设计指标。
因此优化问题可以描述为
约束条件为
3) 汇集导线成本
每一条馈线上所连接的光伏发电单元的数目取决于该条导线所能传输的最大容量,因此每一条馈线上不同汇集处根据传输容量的不同可以选择不同截面类型导线,从而节约汇集导线成本,如图3所示。

图3第j座变电站第i条馈线
因此汇集导线成本为
2.1.2多精英协同进化单亲遗传算法
由上述的详细分析可知,影响光伏电站汇集系统投资成本的因素很多,各因素彼此之间的联系和制约影响较为紧密,这些因素自身为离散变量,并且是非线性关系,故使得拓扑连接优化设计变得异常复杂和困难。而遗传算法具有在全局范围内进行随机搜索的能力,在函数优化问题上优势明显,尤其是求解变量较多的非线性离散问题。
传统遗传算法采用双亲繁殖方式,其主要遗传操作需要两个个体的参与,它在求解组合优化问题时具有局限性;由于组合优化问题通常采用序号编码方式较为方便,而传统遗传算法的常规交叉算子操作会使产生的新个体部分基因缺失以及重复。
单亲遗传算法的所有操作均在单个个体上进行,故使得遗传操作的过程更加简洁,从而使得寻优效率更加高效[14-15]。
本文在此基础上提出一种多精英协同进化单亲遗传算法,算例验证表明,该方法与常规单亲遗传算法相比,寻优效率较高,收敛效果较好。因此采用该方法并借鉴多旅行商问题的求解思路进行拓扑优化设计[16-17]。
1) 确定编码方式与适应度函数
遗传算法的编码方式主要有序号编码和非序号编码两种方式。而序号编码通常用在求解有序组合优化问题。在对汇集系统进行拓扑优化设计时,易对光伏发电单元进行顺序编号,染色体每一位基因与光伏发电单元序号一一对应,且直接反应发电单元之间连接方式,在整个优化求解过程中无需进行复杂的编码和解码操作,因此使得优化设计问题更为简洁方便。
以汇集系统投资成本作为适应度函数,衡量个体优劣。
2) 种群分组遗传操作
将一定规模的种群分成组,在每一组中分别采用最优保存策略的选择方式,当采用最优保存策略时能够保证算法是全局收敛的[14]。对分组中选中的父代最优个体以相应的概率采用基因换位、基因移位和基因倒位等基因重组操作,产生新的个体,将新个体合并完成种群更新。若种群中最优个体已收敛到最优解或者达到进化代数,则算法结束。
3) 多精英协同进化算法步骤
① 初始化种群;
② 计算个体适应度值;
③ 对种群进行分组,应用最优保存策略选择父代个体;
④ 对各个分组中的父代最优个体以一定概率进行基因换位、基因移位和基因倒位等基因重组操作产生新的个体;
⑤ 将各组中产生的新个体合并构成新一代种群;
⑥ 算法终止条件判断,若满足则输出最优解,否则转②。
2.2可靠性评估
可靠性是指某一元件设备或系统在规定运行时间和条件下完成预定功能的一种能力。而电力系统可靠性指的则是电力系统保证不间断的向用户提供符合一定质量标准且满足用户对电量需求的能力[18]。
在规划设计初期,对功率汇集系统拓扑结构进行可靠性分析的目的是在满足经济性最优的情况下保证更高的可靠性,以便设计出既符合经济性最优又符合可靠性较高的拓扑结构;同时,整个光伏电站功率汇集系统实际送出电量将直接影响到电站的经济效益,这在对投资成本回收进行评估时是一个重要的参考指标。
2.2.1可靠性模型
由前述可知,光伏电站功率汇集系统电气设备众多,为了评估拓扑结构可靠性,本文作出相应简化:忽略光照强度的影响,主要考虑光伏发电单元、汇集电缆和开关设备故障情况下,整个光伏电站实际能够送出的功率,而认为其他设备完全可靠。采用蒙特卡洛法进行可靠性分析的优点是在满足一定精度要求情况下,采样次数与系统规模无关,对数学模型要求相对简单[19]。
1) 光伏发电单元可靠性模型
由光伏发电单元构成可知,只要光伏组件、逆变器、升压变压器和连接电缆任一元件故障,整个光伏单元将失效停运。因此光伏发电单元故障率可表示为
2) 汇集电缆组元件可靠性模型
电缆组元件是一个串联系统,它由一段电缆及两侧开关构成,如图4所示。
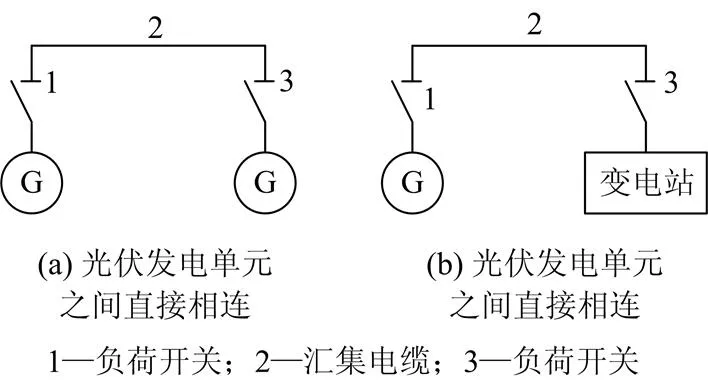
图4电缆组元件电气连接示意图
电缆组元件的等效停运概率可由式(9)描述。
2.2.2可靠性指标
以等效容量作为可靠性评估指标[20],用来衡量汇集系统的实际出力,考察汇集点处的平均出力,计算公式为
数学过程主要包括:
1) 分别设定光伏发电单元和汇集电缆故障率,随机生成故障序列。
2) 判断系统中各元件状态并进行拓扑结构连通性判断。
3) 计算可靠性指标。
由此可得汇集系统拓扑优化设计流程如图5所示。
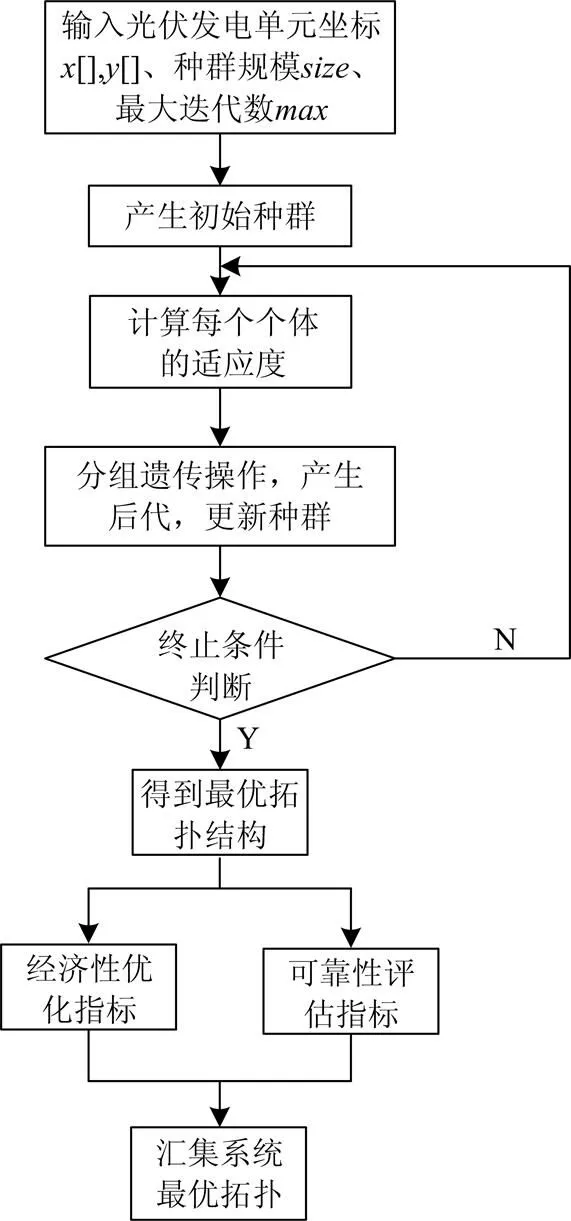
图5汇集系统优化设计流程图
3 算例分析
以某一光伏电站为例,该光伏电站总装机容量为100 MW,一期和二期工程各50 MW。其中500 kW光伏组件接入0.5 MW的并网逆变器,两台逆变器与1 MVA变压器构成1 MW的发电单元,每10个发电单元经集电线路汇集后升压为35 kV,通过2台50 MVA主变升压为110 kV后接入电网。故将整个光伏电站分为10个区域,每个区域内10个光伏发电单元[9]。光伏电站分区如图6所示。

图6光伏电站分区示意图
对区域①内光伏发电单元集电系统按照本文所提方法进行优化设计所得结果如图7所示,其中汇集点代表35 kV中心变电站。

图7集电系统拓扑结构
根据表1及拓扑结构评估指标可确定区域1集电系统拓扑结构为图7中(c)图所示。
表1不同拓扑结构经济性及可靠性结果

Table 1 Results of the economy and reliability analysis for different topologies
分别采用常规单亲遗传算法和多精英协同进化单亲遗传算法的目标函数值收敛曲线如图8所示。从收敛曲线可以看出,采用本文提出的多精英协同进化单亲遗传与常规单亲遗传算法相比,寻优效率更高,收敛效果更好。
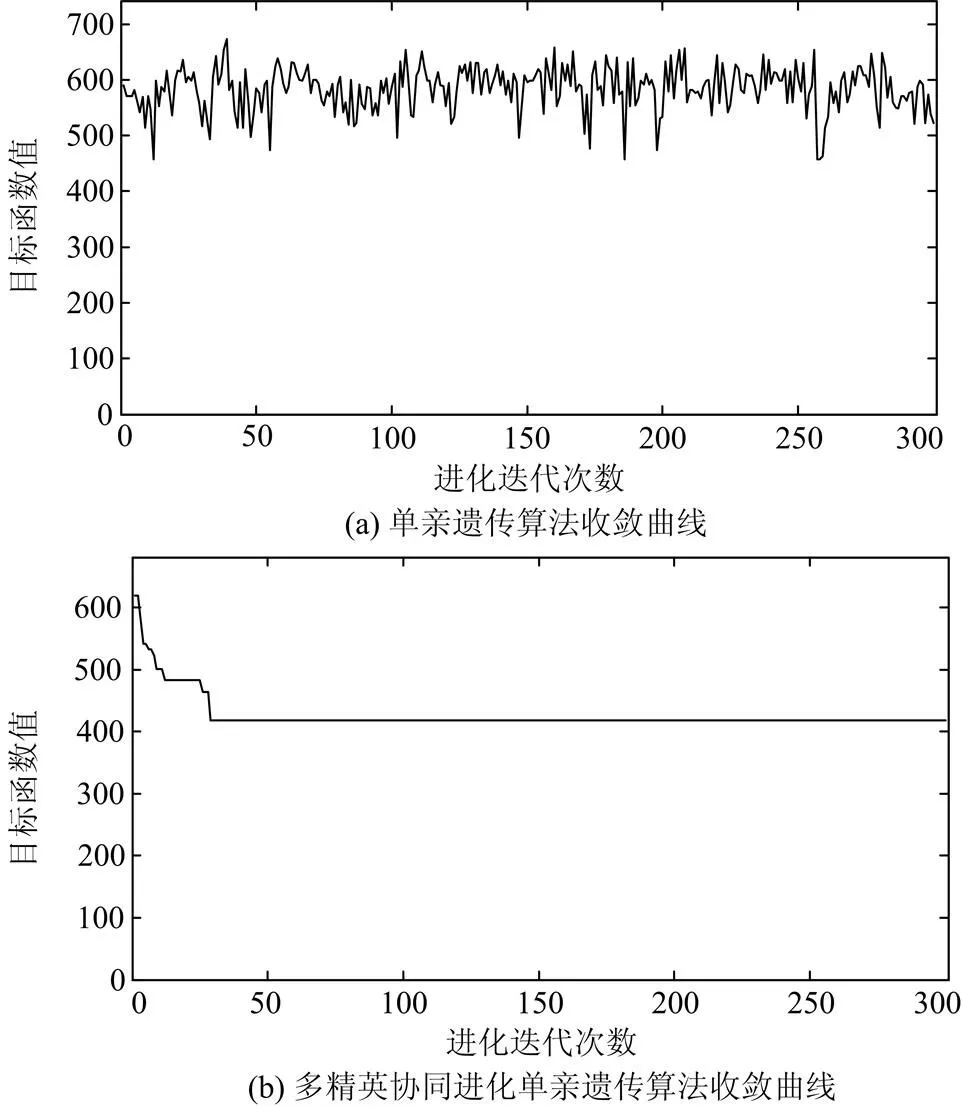
图8目标函数收敛曲线
根据前述方法对图6所示光伏电站分区示意图中各个区域内的光伏发电单元进行经济性优化和可靠性分析,得到经济性及可靠性指标,分别选择不同权重的,,根据式(1),以最小为原则选择拓扑结构,从而得到整个光伏场区功率汇集系统拓扑结构如图9所示。图中光伏单元分布与图6所示区域分布一致,各个区域内的汇集点代表35 kV中心变电站,10个35 kV的中心变电站以每五个为一组采用同样方法汇集到110 kV的终端变电站,最终并入公共电网。

图9光伏场区功率汇集系统拓扑结构
4 结论
本文研究了大型光伏电站功率汇集系统拓扑结构经济性优化和可靠性分析,提出了一种有效的规划设计方法。该方法采用多精英协同进化单亲遗传算法,可得到光伏电站投资经济性指标,采用蒙特卡洛法得到等效容量指标,根据对汇集系统经济性和可靠性的不同权重,可以灵活设置不同的、,以拓扑结构优化设计评估指标最小为原则,进而完成大型光伏电站功率汇集系统拓扑优化设计。采用该方法可以得到多种备选设计方案,根据对汇集系统拓扑结构经济性和可靠性的不同权重,可以灵活确定不同的、,从而为大型光伏电站功率汇集系统拓扑结构规划设计提供参考。
[1] KLEINKAUF W, CRAMER G, IBRAHIM M. PV systems technology —state of the art developments and trends in remote electrification[R]. SMA Technologie AG, 2005.
[2] 王以笑, 张新昌, 路进升, 等. 基于DIgSILENT的并网光伏发电系统的建模仿真[J]. 电力系统保护与控制, 2014, 42(3): 49-55.
WANG Yixiao, ZHANG Xinchang, LU Jinsheng, et al. Modeling and simulation of grid-connected PV system based on DIgSILEN software[J]. Power System Protection and Control, 2014, 42(3): 49-55.
[3] 朱克平, 江道灼. 一种改进型的光伏并网逆变器[J]. 电力系统保护与控制, 2013, 41(6): 99-104.
ZHU Keping, JIANG Daozhuo. An improved inverter for a grid-connected photovoltaic power system[J]. Power System Protection and Control, 2013, 41(6): 99-104.
[4] 孙浩, 张曼, 陈志刚, 等. 并网光伏发电系统的通用性机电暂态模型及其与电磁暂态模型的对比分析[J]. 电力系统保护与控制, 2014, 42(3): 128-133.
SUN Hao, ZHANG Man, CHEN Zhigang, et al. Comparative study on electromechanical and electromagnetic transient model for grid-connected photovoltaic power system[J]. Power System Protection and Control, 2014, 42(3): 128-133.
[5] 姚致清, 于飞, 赵倩, 等. 基于模块化多电平换流器的大型光伏并网系统仿真研究[J]. 中国电机工程学报,2013, 33(36): 27-33.
YAO Zhiqing, YU Fei, ZHAO Qian, et al. Simulation research on large-scale PV grid-connected systems based on MMC[J]. Proceedings of the CSEE, 2013, 33(36): 27-33.
[6] 姚致清, 张茜, 刘喜梅. 基于PSCAD/EMTDC的三相光伏并网发电系统仿真研究[J]. 电力系统保护与控制,2010, 38(17): 76-81.
YAO Zhiqing, ZHANG Qian, LIU Ximei. Research on simulation of a three-phase grid-connected photovoltaic generation system based on PSCAD/TMEDC[J]. Power System Protection and Control, 2010, 38(17): 76-81.
[7] 赵争鸣, 雷一, 贺凡波, 等. 大容量并网光伏电站技术综述[J]. 电力系统自动化, 2011, 35(12): 101-107.
ZHAO Zhengming, LEI Yi, HE Fanbo, et al. Overview of large-scale grid-connected photovoltaic power plants[J]. Automation of Electric Power Systems, 2011, 35(12): 101-107.
[8] 周治. 并网光伏电站子方阵最佳配置选择[J]. 西北水电, 2012(3): 81-87.
ZHOU Zhi. Selection of optimum sub-array arrangement of grid-connected photovoltaic power plant[J]. Northwest Water Power, 2012(3): 81-87.
[9] 白海军. 光伏电站电气一次设计研究[D]. 北京: 华北电力大学, 2013.
BAI Haijun. Photovoltaic power station design research[D]. Beijing: North China Electric Power University, 2013.
[10] 闫凯, 张保会, 瞿继平, 等. 光伏发电系统暂态建模与等值[J]. 电力系统保护与控制, 2015, 43(1): 1-8.
YAN Kai, ZHANG Baohui, QU Jiping, et al. Photovoltaic power system transient modeling and equivalents[J]. Power System Protection and Control, 2015, 43(1): 1-8.
[11]苏剑, 周莉梅, 李蕊. 分布式光伏发电并网的成本/效益分析[J]. 中国电机工程学报, 2013, 33(34): 50-56.
SU Jian, ZHOU Limei, LI Rui. Cost-benefit analysis of distributed grid-connected photovoltaic power generation[J]. Proceedings of the CSEE, 2013, 33(34): 50-56.
[12]史珺. 光伏发电成本的数学模型分析[J]. 太阳能, 2012(2): 53-58.
SHI Jun. Mathematical model analysis of the cost of photovoltaic power generation[J]. Solar Energy, 2012(2): 53-58.
[13] STEMBER L H, HUSS W R, BRIDGMAN M S. A methodology for photovoltaic system reliability & economic analysis[J]. IEEE Transactions on Reliability, 1982, 31(3): 296-303.
[14] 李茂军. 单亲遗传算法理论及应用[D]. 长沙: 湖南大学, 2002.
LI Maojun. The partheno-genetic algorithm theory and application[D]. Changsha: Hunan University, 2002.
[15]李茂军, 童调生. 用单亲遗传算法求解有序组合优化问题[J]. 系统工程与电子技术, 1998, 20(10): 58-61.
LI Maojun, TONG Tiaosheng. A partheno-genetic algorithm solving serial combinatorial optimization[J]. Systems Engineering and Electronics, 1998, 20(10): 58-61.
[16]雷建平, 沈成武, 闻骥骏. 货郎担问题与单亲遗传算法[J]. 武汉理工大学学报, 2003, 25(6): 80-83.
LEI Jianping, SHEN Chengwu, WEN Jijun. Solution TSP in partheno-genetic algorithm[J]. Journal of Wuhan University of Technology, 2003, 25(6): 80-83.
[17]肖鹏, 李茂军, 张军平, 等. 车辆路径问题的单亲遗传算法[J]. 计算技术与自动化, 2000, 19(1): 26-30.
XIAO Peng, LI Maojun, ZHANG Junping, et al. The partheno-genetic algorithm for vehicle routing problem[J]. Computing Technology and Automation, 2000, 19(1): 26-30.
[18]郭永基. 电力系统可靠性分析[M]. 北京: 清华大学出版社, 2003: 1-10.
[19]别朝红, 王锡凡. 蒙特卡洛法在评估电力系统可靠性中的应用[J]. 电力系统自动化, 1997, 21(6): 68-75.
BIE Zhaohong, WANG Xifan. Application of Monte Carlo simulation in power system reliability evaluation[J]. Automation of Electric Power Systems, 1997, 21(6): 68-75.
[20] 陈宁. 大型海上风电场集电系统优化研究[D]. 上海: 上海电力学院, 2011.
CHEN Ning. Research on optimization of power collection system for large-scale offshore wind farm[D]. Shanghai: Shanghai University of Electric Power, 2011.
(编辑 张爱琴)
Multi-objective and hierarchical optimization of power collection system for photovoltaic power plants based on the multi-elite co-evolutionary partheno-genetic algorithm
CHEN Yunchao1, LI Xingyuan1, MIAO Miao1, ZHANG Xiangcheng2, WEN Shengyi3, CHENG Jing3, WANG Xi1
(1. School of Electrical Engineering and Information, Sichuan University, Chengdu 610065, China; 2. State Key Laboratory of Photovoltaic Grid Connected Technology, State Grid Qinghai Electric Power Company, Xining 810008, China; 3. Economic Research Institute, State Grid Qinghai Electric Power Company, Xining 810008, China)
In view of the topological designed problem of power collection system for photovoltaic power plants, the multi-objective and hierarchical optimization based on the multi-elite co-evolutionary partheno-genetic algorithm (MCPGA) is proposed. Firstly, the composition of power collection system is expounded, the corresponding mathematical optimization model is established. Secondly, the MCPGA is used to solve the model, the reliability of collection system is evaluated by Monte Carlo. The economy goal and reliability index are used to evaluate the design of power collection system. At last, simulation results show that this method is effective and practical, convergence of the MCPGA is fast, which can give a coordinate plan of power collection system for photovoltaic power plants.
photovoltaic power plants; power collection system; single parent algorithm; economic optimization; reliability analysis
10.7667/PSPC151440
2015-08-15;
2015-10-31
陈云超(1989-) ,男,通信作者,硕士研究生,研究方向为电网规划及电力系统稳定控制;E-mail: 475369457@ qq.com
李兴源(1945-),男,教授,博士生导师,主要研究方向为电力系统稳定与控制;E-mail: x.y.li@163.com
苗 淼(1982-),男,博士,工程师,主要研究方向为电网规划及电力系统稳定控制。E-mail: miaomiao-5818@ 126.com
国家电网公司科技项目(522830140003)
