基于Pareto原理的HEV能量控制参数NSGA-II多目标优化的研究*

邓 涛，林椿松，李亚南，卢任之

(重庆交通大学机电与车辆工程学院，重庆 400074)

2016087

基于Pareto原理的HEV能量控制参数NSGA-II多目标优化的研究*

邓 涛，林椿松，李亚南，卢任之

(重庆交通大学机电与车辆工程学院，重庆 400074)

以某款并联混合动力汽车为对象，选取8个能量控制参数作为燃油经济性和排放性综合优化参数，提出基于Pareto原理的改进型NSGA-II多目标优化算法，并进行仿真优化。结果表明：优化后燃油消耗率最大降低了11.29%，排放物综合指标最大下降8.78%，其中CO排放的优化效果最显著，下降了24.2%；SOC平衡的误差在0.5%以内，满足约束条件，发动机与电机工作点的效率分布明显改进；同时相比传统加权等单目标优化法，所提出的算法能同时得到多组优化解，为能量管理前期设计提供了更多的选择空间。

混合动力汽车；能量管理；Pareto；NSGA-II多目标优化

前言

混合动力汽车(HEV)能量管理策略是在满足车辆动力性和其它基本要求前提下，根据驾驶员意图和行驶工况，进行不同工作模式切换，控制发动机、电动机/发电机以及蓄电池等部件之间功率流的流动、转换和分配，从全局角度协调控制整车各部件工作状态，实现最优的整车性能，是HEV的核心技术和研究热点之一。当前能量管理控制策略研究大部分都侧重于提高燃油经济性，采用的优化方法包括等效燃油消耗ECMS[1]、动态规划DP、随机动态规划SDP[2]等实现瞬时优化或全局优化，也有其它全局、瞬时或实时优化方法[3]。部分学者指出提高燃油经济性未必就能降低排放，发动机的最大效率区和最小排放区并不完全一致，由此提出了兼顾燃油经济性和排放性的能量管理控制策略[4-7]。还有少数学者进一步分析指出，降低发动机排放物并不等价于减少了尾部排气管排放物，再加上催化器冷却状态时排放转换效率很低，应关注尾部排气管排放物，因此采用DP算法考虑燃油经济性和尾部排气管排放性对能量管理控制的影响[8-9]。

然而，目前不管是针对燃油经济性的单目标优化，燃油经济性和发动机排放性的多目标优化，还是燃油经济性和尾部排气管排放性的多目标优化，绝大多数依然采用的是加权求和的方法，将能量管理控制参数多目标优化问题转换为单目标优化问题，未考虑各目标间的相互影响，且求和后的总目标函数难以反映某些优化目标的真实情况，并不能体现多目标研究的本质。多目标优化的结果应是相互独立、相互排斥的一组最优解集，即某一目标性能优化必然损害其它目标性能。多目标优化得到的最优解集是所有占优解的集合，而非仅有一个最优解。应用Pareto原理解决此问题，能体现出多目标优化的本质。因此本文中将基于Pareto原理的进化算法应用于混合动力汽车能量管理控制经济性与排放性的多目标优化，得到一组非劣Pareto解集克服传统加权方法的缺陷。

本文中以某款并联式HEV为研究对象，建立ADVISOR整车能量管理控制仿真模型，将修改后的NSGA-II进化算法应用于HEV的燃油经济性与排放性的多目标优化之中，克服传统加权方法的缺陷，进一步提升能量管理控制效果。

1 混合动力汽车能量管理控制参数多目标优化

1.1 研究对象

以某款并联混合动力汽车为研究对象，其结构布局如图1所示，整车参数如表1所示。

发动机和电动机通过转矩耦合器，联合驱动车辆(混合驱动模式)；当需求功率较低时，电机可做发电机为电池充电(轻载充电模式)；断开离合器，电机单独驱动车辆(纯电动工作模式)；正常行驶时，电机关闭，发动机单独驱动车辆(发动机单独工作模式)；制动时，断开离合器，电机回收制动能量(再生制动模式)，转换成电能存储在电池组中。

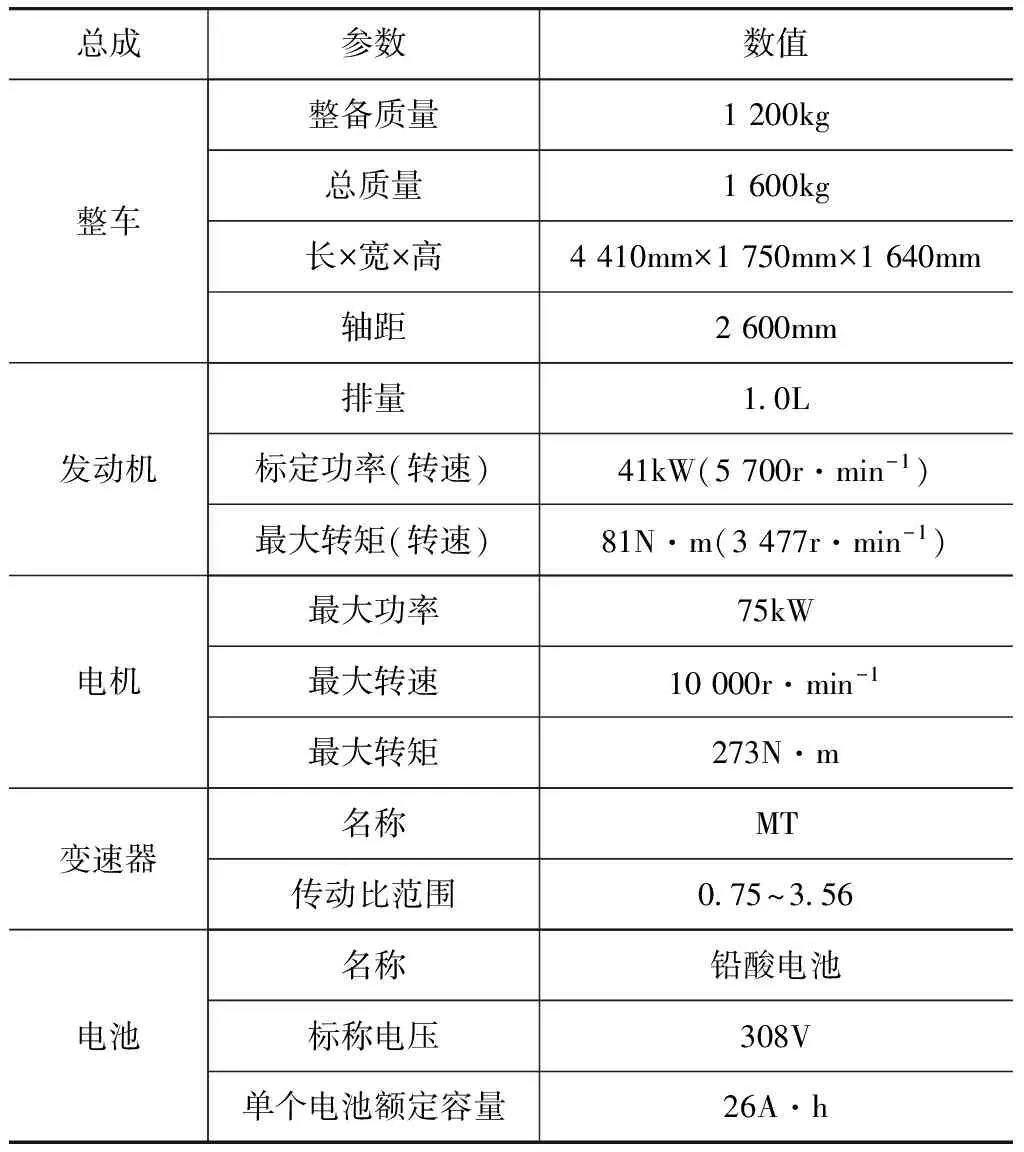
表1 并联ISG型混合动力汽车主要参数

1.2 工作模式分析

工作模式如图2所示，分为：(1)纯电动模式；(2)发动机单独驱动模式；(3)电动助力联合驱动模式；(4)汽车充电模式；(5)制动能量回收模式。

其中各个工作模式中功率、转速与转矩的关系如下。

(1) 纯电动模式 功率需求小，通常为起步阶段，由电动机单独驱动车辆。其转矩与转速的关系为

nw(t)=nm(t)/ρm

(1)

Tw(t)=ρmTm(t)

(2)

Pw(t)=ηmηtηdPm(t)

(3)

(2) 发动机单独驱动 发动机工作在最优工作区间，提供所需功率：

nw(t)=ne(t)/ρ(k(t))

(4)

Tw(t)=p(k(t))Te(t)

(5)

Pw(t)=ηeηtηdPe(t)

(6)

(3) 发动机与电动机联合驱动 电动机起助力作用：

nw(t)=ne(t)/ρ(k(t))=nm(t)/ρm

(7)

Tw(t)=p(k(t))Te(t)+ρmTm(t)

(8)

Pw(t)=ηeηtηdPe(t)+ηmηtηdPm(t)

(9)

(4) 轻载充电模式 电池SOC较低，且发动机输出功率有富余，电动机作为发电机给电池充电：

nw(t)=ne(t)/ρ(k(t))=nm(t)/ρm

(10)

Tw(t)=p(k(t))Te(t)-ρmTm(t)

(11)

Pw(t)ηtηd=ηePe(t)-Pm(t)/ηc

(12)

(5) 制动能量回收模式 发动机停止运行，电动机作为发电机给电池充电：

nw(t)=nm(t)/ρm

(13)

Tw(t)=ρmTm(t)

(14)

Pw(t)ηtηdηc=Pm(t)

(15)

式中：t为行驶时任一时刻；nw为车轮转速；ne为发动机转速；nm为电机转速；ρm为电机速比；Pm为电机功率；Pe为发动机功率；Pw为车辆功率；k(t)为变速器传动比；ρ(k(t))为相应挡位下的总传动比；Te和Tm分别为发动机和电动机输出转矩，耦合后等于车轮的需求转矩Tw；ηe为发动机效率；ηm为电动机效率；ηc为充电效率；ηt为变速器效率；ηd为主减速器效率。

其中主减速器效率取ηd=0.95，变速器效率根据以前实验数据通过插值得到[6]，1-5挡变速器效率map图如图3所示。

1.3 基于Pareto原理的控制参数多目标优化

Pareto最优原理是博弈论中的重要概念，它是指多组最优目标解，不考虑偏好信息时，各组解无优劣之分，这给设计初期提供了更多的选择空间。多目标优化问题中须同时对多个目标进行优化，各个目标之间复杂的关系使传统加权方法有所局限，将Pareto原理引入多目标优化问题中来正好能克服此缺点。基于Pareto原理的NSGA-II算法能够得到多组Pareto解集，对于混合动力的多目标优化问题，此算法能得到比较满意的结果。

多目标优化问题由n个决策变量、m个目标变量和若干约束条件组成，其数学形式为

(16)

式中：x为n维决策矢量，组成n维决策空间；F为m维目标矢量。目标函数F(x)是由m个决策空间到目标空间的映射。

混合动力优化的本质是非线性的多目标优化，本文中以排放和燃油经济性为优化目标，将对汽车性能具有显著影响的几个参数作为优化对象，建立优化函数的表达式：

(17)

式中x为优化参数向量，由于HC和NOx比CO低一个数量级，故将其数值放大9倍。应用NSGA-II算法在Matlab软件中进行仿真，得出Pareto解集，为后期研究开发提供参考数据。

2 基于Pareto的控制参数NSGA-II多目标优化算法

2.1 优化参数的选取

本文中主要选取8个参数进行优化，见表2。

表2 优化参数

2.2 NSGA-II优化算法

目前多目标优化算法很多，其中NSGA-II算法是效果较好、操作更方便而应用最多的一种。以排放和燃油经济性为优化目标，将表2中优化参数作为优化对象，进行燃油经济性和排放性多目标优化，具体优化流程如图4所示。

首先初始化车辆模型，对选取的优化参数进行编码，完成优化参数种群P的初始化；将生成好的种群P依次带入模型中进行求解，返回燃油消耗量和排放物总量作为目标评价值，对两个目标进行非支配排序，并计算拥挤距离，得出个体优劣评价的序列层和拥挤距离，完成对初始化种群的处理；然后在已有初始种群的基础上进行进化操作。采用二联赛的方法在初始种群P中选取种群数量的一半作为进化的父母代，然后对选取的父母代进行交叉变异操作，生产子代种群Q；将生成的子代带入模型进行求解，返回目标值，然后把父代P与子代Q合并成一个新的临时种群，对其进行非支配排序计算拥挤距离，评价个体优劣性；在个体优劣的基础上进行进化，获取与原种群数目相同的个体N。完成一次进化迭代，在没有达到设定的最大进化代数时，重复上面进化操作，直到满足结束条件或进化代数达到设定值为止，输出最优Pareto解集。

3 基于Pareto的NSGA-II多目标优化仿真分析

3.1 并联混合动力汽车仿真建模

以发动机的数学模型为基础，根据稳态工况下的发动机特性实验数据建立发动机模型，发动机外特性转矩通过最小二乘法拟合成转速的一元函数。

(18)

式中：k为拟合阶数；Ai为拟合系数。

万有特性是发动机分析的重要依据，通常可根据转矩与转速拟合成曲面；但应用更多的形式是纵坐标为转矩、横坐标为转速的一族燃油消耗率等高线的曲线图。燃油消耗率的表达式为

(19)

式中：ge为燃油消耗率；Ak为万有特性数学模型中的拟合系数，其中k=(j+1)(j+2)-j-1+i；s为模型阶数。

由此可得发动机燃油消耗和发动机污染物排放特性为

(20)

j-1-l)Telnej-l

(21)

式中：Pe为发动机功率；E为污染物的排放率；k2为排放模型中污染物的拟合系数。

由此可得污染物排放：

(22)

(23)

(24)

根据式(18)～式(24)，可建立发动机仿真模型，如图5所示，结合式(1)～式(17)，可建立整车模型仿真模型，如图6所示。

3.2 仿真分析

在UDDS市区循环工况下进行仿真分析，得到工况跟随结果(图7)、SOC变化情况(图8)、功率变化情况(图9)、Pareto最优解集(表3)、发动机优化前后工作点效率分布图(图10)和电机优化前后工作点效率分布图(图11)等仿真或优化结果。

由图7可见，实际仿真车速能很好地跟随目标车速，并且误差非常小，具有良好的工况跟随能力。

仿真时选取10次仿真结果最优解集，汇总后得到的Pareto最优解集如表3所示，并从中又挑选5组最优解集绘出SOC的变化曲线，如图8所示。可见SOC变化平滑，且SOC平衡约束误差在0.5%以内，满足荷电平衡的要求。

为了解功率变化情况，可在以上10组Pareto最优解集选取其中一组，进行仿真可得到功率变化。

本文中选取第5组，如图9所示。

表3中，第0组为车辆默认设置及性能指标，第1～10组为优化后的最优Pareto解集。观察表中数据可以发现，在保证系统基本性能的前提下，整车的性能均得到提升。燃油经济性和排放性能都在一定程度上得到改善，其中燃油消耗最大下降了11.29%；排放物综合指标最大下降了8.78%，其中，CO降低的效果最为明显，达到24.2%，HC和NOx排放有所下降，结果如表4所示。

表4 最大优化比例

与表3中所列的10组最优优化方案相比，结果上的差距并不大，但是在设计匹配上有多种不同的选择方案，在优化性能的同时拓展了设计方案。

同时选取第5组最优解分析发动机的工作点及其效率分布情况，结果如图10所示。

由图10可见，优化后的发动机工作效率有所提高，并且低效率点(0.15-0.2区间内)明显减少，且工作点相比优化前有所减少(优化前有效工作点960个，优化后有效工作点700个)，原因在于电机工作点增加，电机工作点和效率分布情况如图11所示。

由此可知，优化后能进一步改善发动机和电机两者协调工作性能，进一步提高整车工作效率。

此外，本文中提出的混合动力多目标优化算法具有通用性，适用于其它混合动力系统、电动汽车系统和其它多目标优化控制领域。

4 结论

(1) 针对混合动力汽车能量管理控制燃油经济性与排放性优化过程中将多目标加权转化为单目标问题而存在的缺点，提出NSGA-II多目标优化算法，避免各目标间的相互影响而不能得到需要的解集；通过优化参数，得到10组最优Pareto解集。

(2) 将得到的Pareto解集与初始解比较可以发现，在满足基本性能的前提下，其燃油消耗最大下降了11.29%，排放物综合指标最大下降了8.78%；并且10组Pareto解集也为设计者提供了更多的选择方案，在混合动力的个性化设计上拓展了更大的选择空间。

(3) 仿真结果表明，仿真具有良好的工况跟随能力，SOC变化满足小于0.5%的约束条件，优化后的发动机和电机工作点效率明显提升。

(4) 在Pareto最优解集的分布性(Pareto前沿)上还有待提升，对设计方案上有进一步改善的余地，如何得到分布性更好的Pareto前沿面有待进一步研究。

[1] 李翔晟,陈斗,周永军.基于最小瞬时等效燃油消耗的液压混合动力车辆能量管理策略[J].公路交通科技,2012,29(12):148-152,158.

[2] 张炳力,张平平,赵韩,等.基于离散动态规划的PHEV燃油经济性全局最优控制[J].汽车工程,2010,32(11):923-927.

[3] XU Liangfei, YANG Fuyuan, LI Jianqiu, et al. Real Time Optimal Energy Management Strategy Targeting at Minimizing Daily Operation Cost for a Plug-in Fuel Cell City Bus[J]. International Journal of Hydrogen Energy,2012,37(20):15380-15392.

[4] HE Hongwen, TANG Henglu, WANG Ximing, et al. Global Optimal Energy Management Strategy Research for a Plug-In Series-Parallel Hybrid Electric Bus by Using Dynamic Programming[J]. Mathematical Problems in Engineering,2013,2013(1):1-11.

[5] WALSH P M. Plug-in Hybrid Electric Vehicle Supervisory Control Strategy Considerations for Engine Exhaust Emissions and Fuel Use[D]. Virginia: Virginia Polytechnic Institute and State University,2011.

[6] 秦大同,隗寒冰,段志辉,等.重度混合动力汽车油耗和排放多目标实时最优控制[J].机械工程学报,2012,48(6):83-89.

[7] MICHEL Pierre, CHARLET Alain, COLIN Guillaume. Energy Management of HEV to Optimize Fuel Consumption and Pollutant Emissions[C]. 11th International Symposium on Advanced Vehicule Control, AVEC’12, Seoul, Korea,2012:1-6.

[8] KUM Dongsuk, PENG Huei, BUCKNOR Norman K. Supervisory Control of Parallel Hybrid Electric Vehicles for Fuel and Emission Reduction[J]. Journal of Dynamic Systems, Measurement, and Control,2011,133(6).

[9] KUM Dongsuk, PENG Huei, BUCKNOR Norman K. Optimal Catalyst Temperature Management of Plug-in Hybrid Electric Vehicles[C]. American Control Conference on O’Farrell Street, San Francisco, CA, USA,2011.

A Research on NSGA-II Multi-objective Optimization forHEV Energy Management Parameters Based on Pareto Principle

Deng Tao, Lin Chunsong, Li yanan & Lu Renzhi

SchoolofMechatronics&AutomotiveEngineering,ChongqingJiaotongUniversity,Chongqing400074

With a parallel hybrid electric vehicle as objective, eight energy management parameters are chosen as comprehensive optimization parameters for fuel economy and emission performance, an improved NSGA-II multi-objective optimization algorithm based on Pareto principle is proposed, with a simulation optimization conducted. The results show that after optimization, the fuel consumption decreases by 11.29% at most, the overall emission indicator lowers by 8.78% at most, in which the optimization effectiveness of CO emission is most significant, reducing by 24.2%, the SOC deviation is within 0.5%, meeting its constraint condition, and the distribution of working points and their efficiency for both engine and motor are obviously improved. In addition, compared with single objective optimization algorithms including traditional weighting scheme, the algorithm proposed can obtain much more optimized solution sets, hence providing much more options to choose in preliminary design of HEV energy management.

HEV; energy management; Pareto; NSGA-II multi-objective optimization

*国家自然科学基金(51305473)、中国博士后科学基金(2014M552317)、重庆市博士后研究人员科研项目(xm2014032)、重庆市科委基础与前沿研究计划项目(cstc2013jcyjA60007)和重庆市教委科学技术研究项目(KJ120421)资助。

原稿收到日期为2014年9月18日，修改稿收到日期为2014年12月30日。