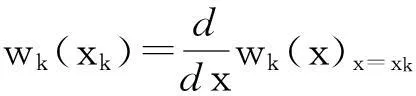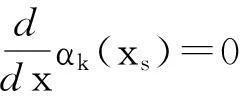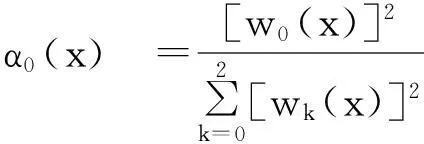二阶切触有理插值算子的构造方法

马锦锦

(安徽建筑大学数理学院，安徽　合肥　230601)



二阶切触有理插值算子的构造方法

马锦锦

(安徽建筑大学数理学院，安徽合肥230601)

[摘要]通过引入二阶插值算子，给出了一种较为简便的构造切触有理插值的新方法和一个新型的切触有理插值公式.如果用该方法所得到的插值函数次数较高，还可以通过引入多个参数的方法，对所构造的有理插值函数进行降次.该方法比常用的连分式方法更为简便易行，具有较高的实用价值.

[关键词]二阶插值算子；切触有理插值；降次；参数；连分式

已有的切触有理插值研究方法大多是基于连分式的方法[1-3].这些方法运算量较大，并且运算也会受到特定条件的限制，不便于实际操作.因此，本文引入二阶插值算子，给出一种较为简便的构造切触有理插值的新方法.

首先讨论切触有理插值问题.

定义1切触有理插值[4]

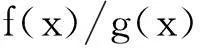
l=0,1,…,sk-1

k=0,1,…,m

切触有理插值理论与应用是有理逼近领域的核心构成部分，是计算数学中最引人关注的课题.切触有理插值是对一般有理插值的推广[4]，类似多项式插值中的Hermite插值[5].尽管切触有理插值比一般有理插值形式复杂，但应用性更强，在量子力学、量子场论、原子和分子物理、控制论和数值分析等领域都有非常广泛的应用.

1构造切触有理插值算子

传统方法构造的切触有理插值比一般有理插值形式复杂，在应用过程中带来很多不便，比如结构繁琐、计算量大.为了克服这些缺点，本节利用多项式插值来构造插值基函数，引入一种新型的二阶插值算子，用于构造切触有理插值函数.如果所构造的切触有理插值次数较高，我们可以通过引入参数的方法，将所构造的切触有理插值函数的分子分母同时降低次数.由于本节所构造的切触有理插值可以通过多次降次来化简，给出形式较为简洁的低次切触有理插值，因而在实际应用中可以大大地减少计算量.

步骤1：给出用于构造插值基函数的多项式插值.

构造多项式插值如下：

对于给定的x0

wk(x)=(x-x0)…(x-xk-1)(x-xk+1)

…(x-xm),

(1)

以上所构造的多项式插值wk(x)满足

1)

wk(xs)=0,

k≠s,k,s=0,1,…,m.

2)

这种多项式插值的特性有助于插值基函数的构造.

步骤2：构造插值基函数

(2)

其中

Q(x)=[w0(x)]2+…+[wk(x)]2+

(3)

以上所构造的插值基函数αk(x)满足

1)

(4)

k,s=0,1,2,…,m.

2)

(5)

k,s=0,1,2,…,m.

通过这种方法给出的插值基函数形式简洁，规律性强，便于构造切触有理插值.

步骤3：引入二阶插值算子，构造切触有理插值函数.

给定x0

给出二阶插值算子为

pk(x)=f(xk)+f′(xk)(x-xk)

+f″(xk)(x-xk)2

(6)

(k=0,1,2,…,m)

则(6)式满足

pk(xk)=f(xk)，

p(l)(xk)=f(l)(xk)

(7)

(l=0,1,2)

用以上构造的二阶插值算子，给出插值公式如下：

(8)

(8)式即为利用二阶插值算子所构造的插值公式.

经过验证

R(l)(xs)=f(l)(xs)

(9)

l=0,1,2.

(8)式中所构造的切触有理插值函数结构简单，且应用无条件制约.而传统的连分式方法计算必须先假定计算中每一步的可行性，如分母是零的情况不会出现，而实际计算前根本无法判定.本节给出的新型切触有理插值构造法很好地避免了连分式方法的这一缺点.

例1给出节点以及相应的函数值、导数值如下：

x0=1，f(x0)=0，f′(x0)=1，f″(x0)=2；

x1=0，f(x1)=1，f′(x1)=2，f″(x1)=3；

x2=2，f(x2)=2，f′(x2)=0，f″(x2)=1.

解由 (6) 式可求二阶插值算子

p0(x)=0+(x-1)+2(x-1)2

p1(x)=1+2(x-0)+3(x-0)2

p2(x)=2+0(x-2)+1(x-2)2

由(1)、(2)、(3)式知

通过 (7) 式可求出

(10)

经过验证

R(l)(xs)=f(l)(xs)，l=0,1,2，s=0,1,2.

(10)式中的切触有理插值函数R(x)是我们通过引入二阶插值算子得到的有理插值函数.从上述实例中可以看出，本文给出的切触有理插值构造方法思路简单、清晰，构造的切触有理插值函数形式较为简洁，且其应用并不像连分式方法一样的约束条件，因此应用范围广，具有较高的应用价值.

我们也可以对所构造的切触有理插值函数进行降阶，给出普遍适用的降阶方法.用这种降阶方法可以灵活地引入参数，降低所构造的切触有理插值函数分子分母的次数，也可以通过该降阶方法，连续多次对插值函数进行降阶，得到次数符合应用需求的切触有理插值函数.

步骤4：引入参数，给出降低切触有理插值函数分子分母次数的一般方法.

给定节点x0

(11)

满足插值条件

R(l)(xs)=f(l)(xs)，l=0,1,2.

例2对例1中用二阶插值算子构造的有理分式函数R(x)进行降次.

解

由(11)式知

令2β0+3β1+β2=0，将有理分式进行降次，则β0=-2,β1=1,β2=1.

故得

(12)

上式中，分子次数为5次、分母次数为2次，而(10)式中所构造的原始插值函数的分子次数为6次、分母次数为4次，通过该方法实现了降次.可以通过多次降阶的途径得到满足应用需求的切触有理插值函数.由于该方法可以灵活地降低切触有理插值函数的次数，故其应用范围很广.我们可以将本文所构造的切触有理插值用于模糊控制和估计复杂系统的可靠性中，利用切触有理插值新方法建立新型插值控制算法.这种算法下的控制器具有设计简单、不需要选择具体隶属函数、不需要过多的专家经验等好处，可以得到很好的控制效果，在实际生产中有更大的灵活性和更高的应用价值.

2结论

(12)式中降阶所得有理分式比(10)式中原始切触有理插值函数的分子分母次数明显降低.这充分说明了上述通过引入参数实现对有理函数分子、分母进行降次的方法是十分有效和实用的，而且操作方便，计算量不大.

本文通过引入二阶插值算子，给出的构造切触有理插值函数方法比常用的连分式方法更为简便易行，给出的插值公式也较为实用.我们也可以将这种思想方法继续推广，给出高阶的插值算子，用于解决更为复杂的切触有理插值问题.本文所给出的切触有理插值构造的新方法由于结构简洁，降阶规律性强，需要的计算量较小，因此在模糊控制论[6]、图像压缩与重建、有理曲线和曲面生成以及复杂系统性能评估等领域都有较高的应用价值[7].

[参考文献]

[1]王仁宏，朱功勤. 有理函数逼近及其应用[M].北京：科学出版社，2004.

[2]MAINAR E，PENA P M. A basis of C-Bezier splines with optimal properties[J].Computer Aided Geometric Design，2012，19(4):291-295.

[3]WANG G Z，CHEN Q Y，ZHOU M H. NUATB-spline curves[J].Computer Aided Geometric Design，2004，21 (2):193-205.

[4]朱功勤,马锦锦.构造切触有理插值的一种方法[J].合肥工业大学学报(自然科学版)，2006，29(10) :1320-1326.

[5]陈之兵. Salzer定理的二元向量形式[J]. 数学研究评论，2003，23(2):233-236.

[6]史健，黄丽，李中夫.模糊控制与插值[J].四川大学学报(自然科学版)，2009，12(5):646-650.

[7]杨文光，赵海良. 基于样条插值的模糊控制算法[J]. 模糊系统与控制，2009，23(3):152-157.

(责任编辑穆刚)

A method of constructing bivariate osculatory rational interpolating operator

MA Jinjin

(College of Mathematics & Physics, Anhui Jianzhu University, Hefei Anhui 230601, China)

Abstract：In this paper, osculatory rational interpolating function was constructed by a new method of introducing bivariate interpolating operator. For osculatory rational interpolating function that we had constructed, we could reduce its number of times by choosing parameters. Existing methods of constructing osculatory rational interpolating function were almost related to calculation of continued fractions. But the feasibility of their algorithms was conditional and they needed a large amount of calculation. This new method in this paper was fairly simple and had immense application foreground.

Key words：bivariate interpolating operator; osculatory rational interpolation; deflation; parameter; continued fractions

[中图分类号]O174.42

[文献标志码]A

[文章编号]1673-8004(2016)02-0037-03

[作者简介]马锦锦(1981-)，女，安徽临泉人，讲师，硕士，主要从事应用数值逼近方面的研究.

[基金项目]安徽省高等学校省级自然科学研究项目(KJ2013B067).

[收稿日期]2015-07-30