三指灵巧手运动学与动力学仿真研究

陈　玉，夏发银

(安徽工程大学机械与汽车工程学院， 安徽　芜湖　241000)



三指灵巧手运动学与动力学仿真研究

陈玉，夏发银

(安徽工程大学机械与汽车工程学院， 安徽芜湖241000)

[摘要]仿照人类手指结构，设计出三指灵巧手的机械结构.灵巧手每个关节由电机驱动，手指结构接近于人手，每个手指具有4个自由度.进行单指运动学分析，得到坐标变换矩阵，通过Adams软件进行单指位姿和指尖位移仿真.通过对灵巧手的动力学分析，利用Adams软件对单指弯曲这一常见动作进行动力学仿真.仿真结果表明：灵巧手设计结构合理，有较大工作空间，动作灵活，可实现多种灵巧操作.

[关键词]灵巧手；运动学；Adams仿真；动力学

与传统机械手相比，机器人灵巧手抓取方式较为灵活，能够对形状复杂的物体进行精确控制，抓取稳定性也较好，能基本替代人类在特定环境下进行作业，如太空、核电站、化工厂等工作环境[1].人手经过自然界的选择与进化，具有很强的优越性.机械灵巧手仿照人手设计的理念，每个手指具有3个指节和3个关节，与人手的情况一致[2].

在灵巧手运动学模型研究方面，主要有DH模型、MDH模型等[3].MDH模型有一定的缺陷，即相邻关节轴线夹角在90°附近时无法适用．由Denavit与Hartenberg[4]提出的DH模型，由于其物理意义明确、编程较为容易，应用较广.

关于灵巧手动力学模型方面，国内外都做了很多研究.余麟等采用Newton-Euler方法对灵巧手进行逆动力学分析，演算出其动力学方程[5].王华等人利用切片理论对水下灵巧手进行动力学分析，并通过Matlab软件中的SimMechanics进行验证[6].针对没有考虑摩擦力影响的动力学模型，李立全等运用拉格朗日动力学方法完成动力学逆解计算[7].Joseph C.Chan提出一种巧妙的动力学模型用以解决碰撞、接触及滑动等问题[8].根据机器人动力学的基本原理，本文进行灵巧手的动力学仿真.仿真结果表明，本文设计的灵巧手结构较为合理，抓取能力也较强.

1灵巧手的机械结构

人类的手指，五指皆不相同，将其运用于机械灵巧手中会有诸多不便.本文设计了一种由3个机械结构完全相同的手指、1个手掌和1个手腕组成的灵巧手.考虑到人类的食指、中指、无名指、小指皆为3个关节，故在此也将机械灵巧手的每个手指关节设计为3个，具体参数如表1所示.为了增强灵巧手的能力，手腕设计与人类略有不同，设计为转动角度更大、更灵活，即可以旋转360°.图1为三指灵巧手的自由度简图.

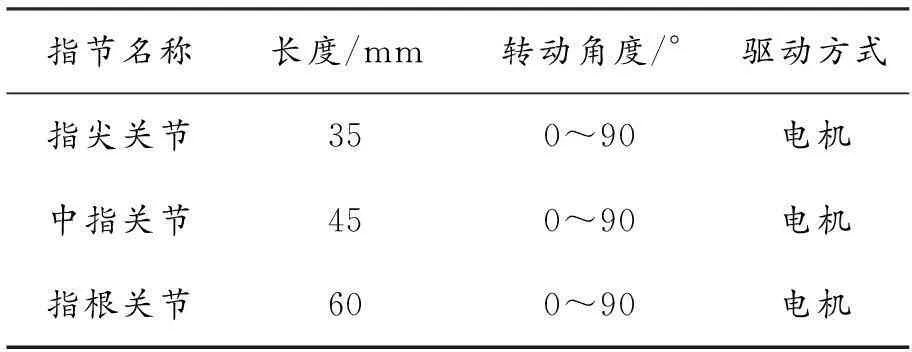
表1　指关节参数

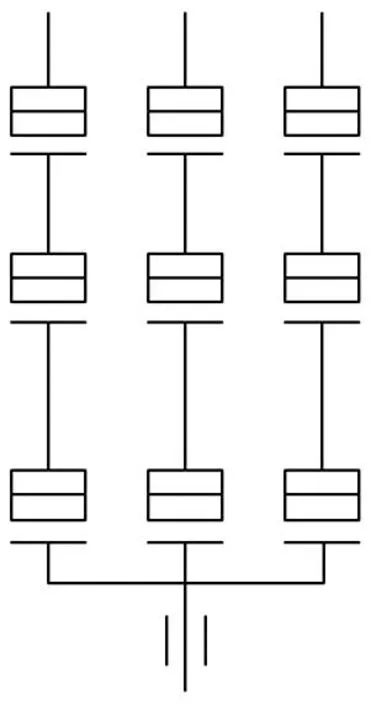
图1　三指灵巧手自由度简图

2灵巧手的运动学模型及仿真结果

2.1灵巧手运动学模型

依据机器人的运动学原理，根据自然人手的特性建立单指三连杆模型进行分析[9]，通过调整3个关节的弯曲角，可使手指指端达到指定位置[10].本文采用DH法对三指灵巧手进行运动学分析.由于本文的灵巧手在设计上令每一个手指结构都一样，所以文中只对单指进行分析.图2为运动示意图，x0y0z0为固定参考坐标系，坐标系x1y1z1、x2y2z2、3y3z3为动坐标系.

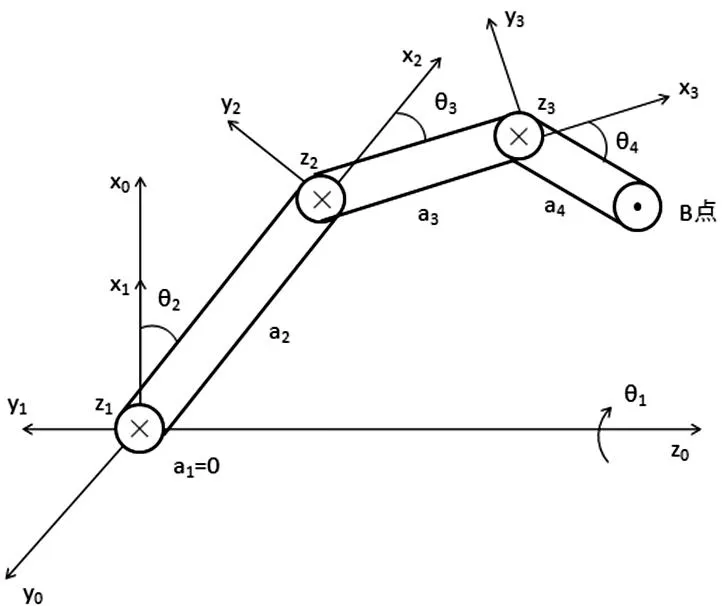
图2　单指运动示意图

a1、a2、a3和a4表示的是每个指节的长度，θ1、θ2、θ3和θ4表示的是每个关节的转角角度.其中，指根关节侧摆的角度由θ1表示，指根、中指和指尖屈曲的角度由θ2、θ3和θ4表示，αi是扭转角，di是连杆距离.假设单指的指尖点(B点)在坐标系x0y0z0中的坐标为 (px, py, pz)，对应的D-H参数如表2所示.

表2　单指机构D-H参数

公式(1)表示的是每个关节的齐次变换矩阵Ai：

Ai=Rot(z,θi)×Trans(0,0,di)×

Trans(ai,0,0)×Rot(x,αi)

(1)

将各参数代入 (1) 式，求得Ai为：

(2)

将表1中的各个参数代入公式(2)当中，可以分别得出公式(3)、(4)、(5)、(6)，也就是A1、A2、A3、A4.

(3)

(4)

(5)

(6)

指尖B点由指根关节a1开始变换直至指尖关节a3，中间经过中指关节a2， 将A1、A2、A3、A4连乘即可得到B点相对于坐标系x0y0z0的变换矩阵T40：

T40=A1A2A3A4=

(7)

上式中，ci=cosθi,si=sinθi,cij=cos(θi+θj),sij=sin(θi+θj),cijk=cos(θi+θj+θk),sijk=sin(θi+θj+θk).其中，i,j,k=2,3,4.

由于公式(7)较为复杂，可以采用以下方式简化B点的坐标变换矩阵.B点的位姿由向量p表示，指尖在坐标系x0y0z0中的姿态需要用正交向量n、方向向量o和接近向量m等3个向量来共同表示，见公式(8)：

(8)

上式中，nx=c1c234, ny=s1c234, nz=-s234, ox=-c1s234, oy=-s1s234, oz=-c234, mx=s1, my=-c1, mz=0, px=(a4c234+a3c23+a2c2)c1, py=(a4c234+a3c23+a2c2)s1, pz=a4s234+a3s23+a2s2.

2.2灵巧手运动学仿真结果

若手指每个指节的长度和转角为已知条件，可以通过公式(8)求得指尖在空间中的位姿.若要查看手指指节中心点的运动情况，可以在指节内表面中心点建立一个标记点，然后以该标记点为测量对象，测量各运动参数[11].图3表示的是手指位姿变换情况.图4为手指弯曲动作时，手指由图3中左上图运动至右下图时，指尖相对于关节2(即指根关节)的xz方向位移.

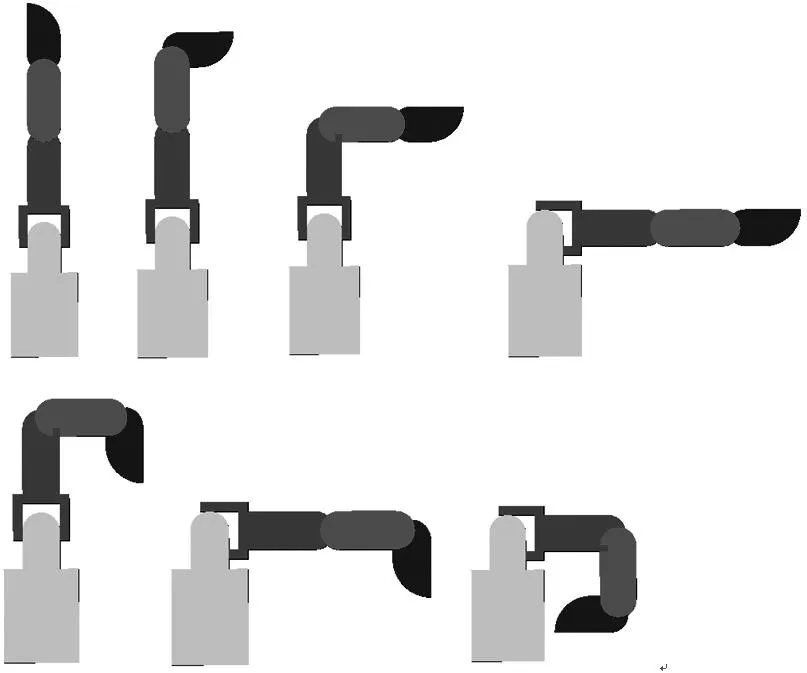
图3　三指灵巧手基本位置与姿态

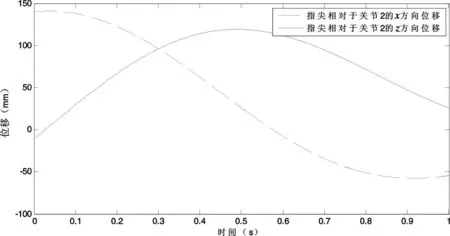
图4　指尖相对于关节2的xz方向位移

3灵巧手的动力学模型及仿真

3.1灵巧手动力学模型

本文采用拉格朗日—欧拉法对灵巧手的动力学进行分析.由于在结构设计上，本文中的灵巧手中每个手指的结构都一样，故而仅仅建立了如图2所示的单指动力学模型.x0y0z0、x1y1z1、x2y2z2和x3y3z3表示的是每个关节的坐标系，τ1、τ2、τ3和τ4表示的是每个关节的驱动力.可得单指的动力学方程：

τ(t)=D(q(t))q″(t)+h(q(t),q′(t))+c(q(t))

(9)

上式中，τ(t)表示的是4×1维的驱动力矢量，q(t)表示的是关节变量矢量，q′(t)表示的是关节速度矢量， q〃( t )表示的是关节加速度的矢量，D(q)表示的是与加速度相关的4×4维的对称矩阵，h(q,q′) 表示的是4×1 维的科氏力和向心力矢量，c(q)表示的是4×1维的重力矢量.

由于公式(4)的灵巧手单指动力学方程具有高度非线性和多输入多输出耦合系统等特点，故而模型很复杂.本文利用ADAMS软件对灵巧手进行动力学仿真.

3.2灵巧手动力学仿真结果

在人类手指的动作中，单指弯曲动作很常用，而且在灵巧手夹持工器夹具时也基本都会有此动作，本文以此动作作为研究对象.主要考虑两个方面：一是指尖仅受重力时，二是同时受外力和重力时.分别分析每个关节的受力情况，得出每个关节的驱动力矩[12].图5中左图所示为手指的初始状态，而右图则表示单指弯曲这一动作的最终状态.在整个动作过程中，由于不需要在Y方向运动，故而关节1是没有任何动作的，即关节1所受力矩始终为零，在此不对关节1做任何分析与研究.只研究关节2、3、4所受力矩.

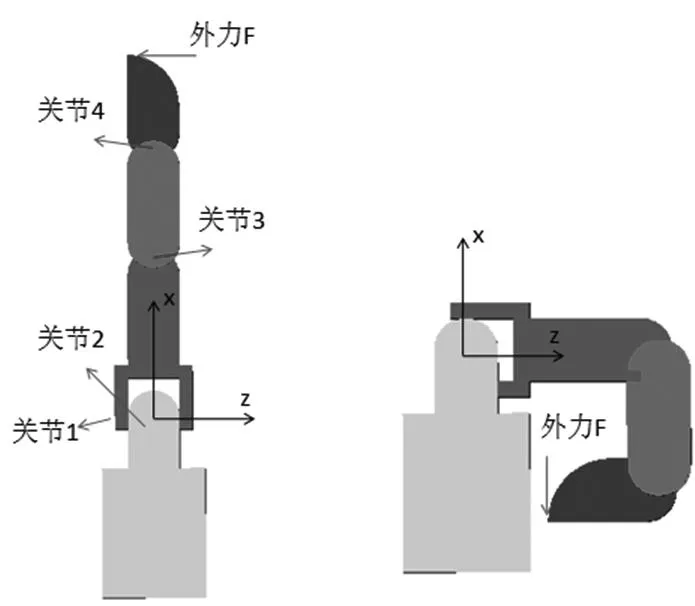
图5　单指弯曲过程与坐标系

根据第1节的内容以及表1的数据可以得出，灵巧手食指各指节的长度和质量分别为：第一指节的长度是35mm，质量是0.105 4kg；第二指节的长度是45mm，质量是0.163 7kg；第三指节的长度是60mm，质量是0.269 7kg.假设整个动作过程中每个关节均作匀角速运动.

3.2.1指尖仅受重力作用状态

首先考虑指尖不受任何外力，仅受重力的状态下运动过程中每个关节的力矩变化情况.每个关节所受到的力矩都在不断变化.图6为力矩具体的变化曲线图.从图6中可以看出：

(1)每个关节在0秒时力矩都是最大的，其力矩分别为τ2max=337.05 N·mm，τ3max=94.75 N·mm，τ4max=14.51 N·mm；

(2)每个关节的力矩都在不断变化，且变化都很平滑；

(3)每个关节都有力矩为零的情况.

造成上面3种情况的原因如下：

(1)所受力矩是力与力臂的乘积，当手指处于初始状态时，力臂的数值最大.

(2)所受力矩是力与力臂的乘积，由于关节所受力始终不变，而在运动过程中力臂的数值在不断变化，所以每个关节所受的力矩也在不断变化.

(3)出现力矩为零的现象，说明该关节于此刻所受的力或者其力臂的数值至少有一个为零.有两种情况的发生会出现力矩为零的现象：一是当重力与指节的方向相同，二是每个指节力矩相互抵消.

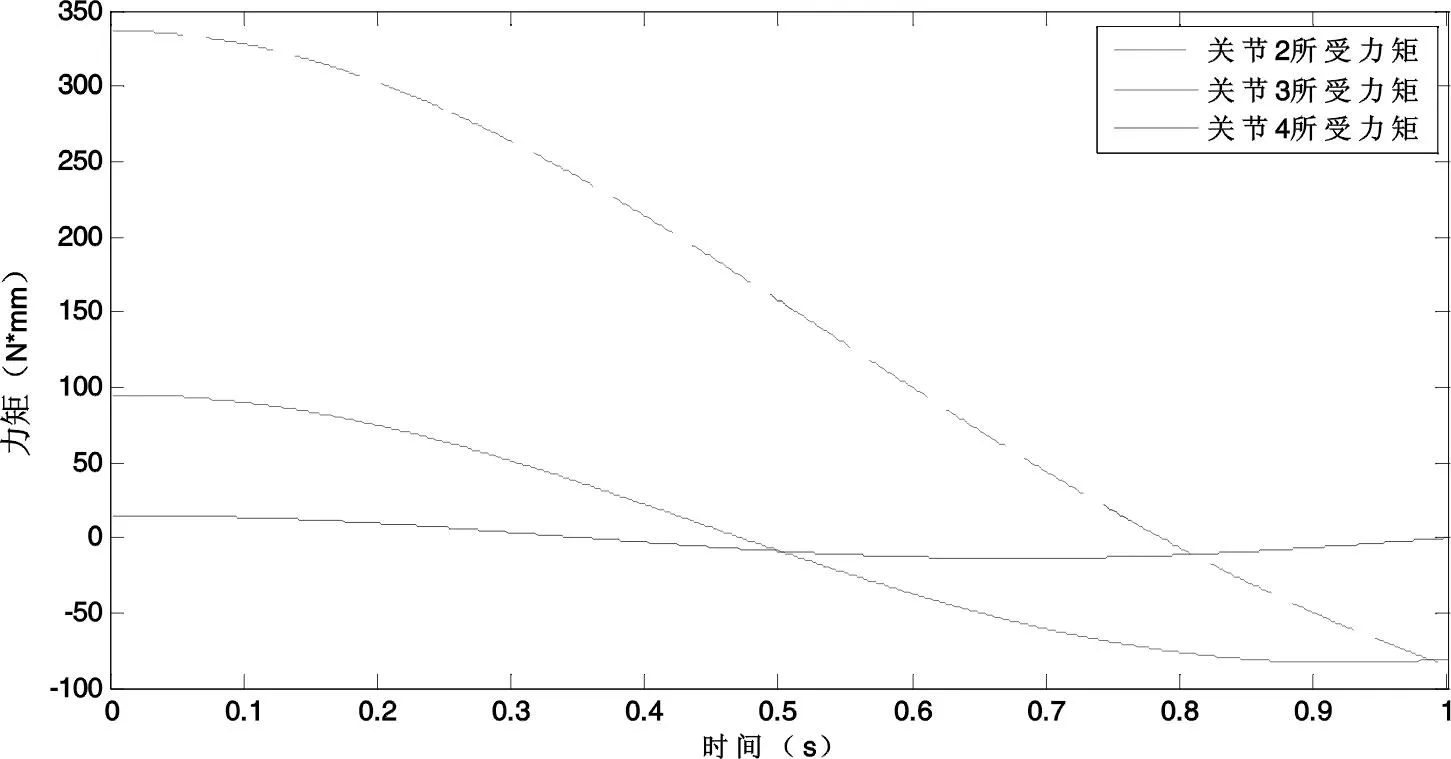
图6　指尖没有施加外力时关节2、3、4所受力矩

3.2.2指尖受到重力与外力同时作用的状态

在重力和外力F=5 N(10 N)的共同作用下，单指从初始位姿到最终位姿时，每个关节所受到的力矩曲线变化情况如图7和图8所示.图7和图8与图6的曲线略有相似，但力矩的数值发生了明显的变化.与前一种情况仅受重力作用的状态时相比，每个关节所受到的力矩明显变大.但在初始位姿时，每个关节的力矩仍然是最大的，即τ2max=1 037 N·mm，τ3max=491.32 N·mm，τ4max=189.51 N·mm(τ2max=1 737 N·mm，τ3max=887.89 N·mm，τ4max=364.51 N·mm).

经过以上对灵巧手所进行的动力学仿真，可以得出每个关节的驱动力矩，可以用于灵巧手的伺服电机选取、控制和可靠性分析.

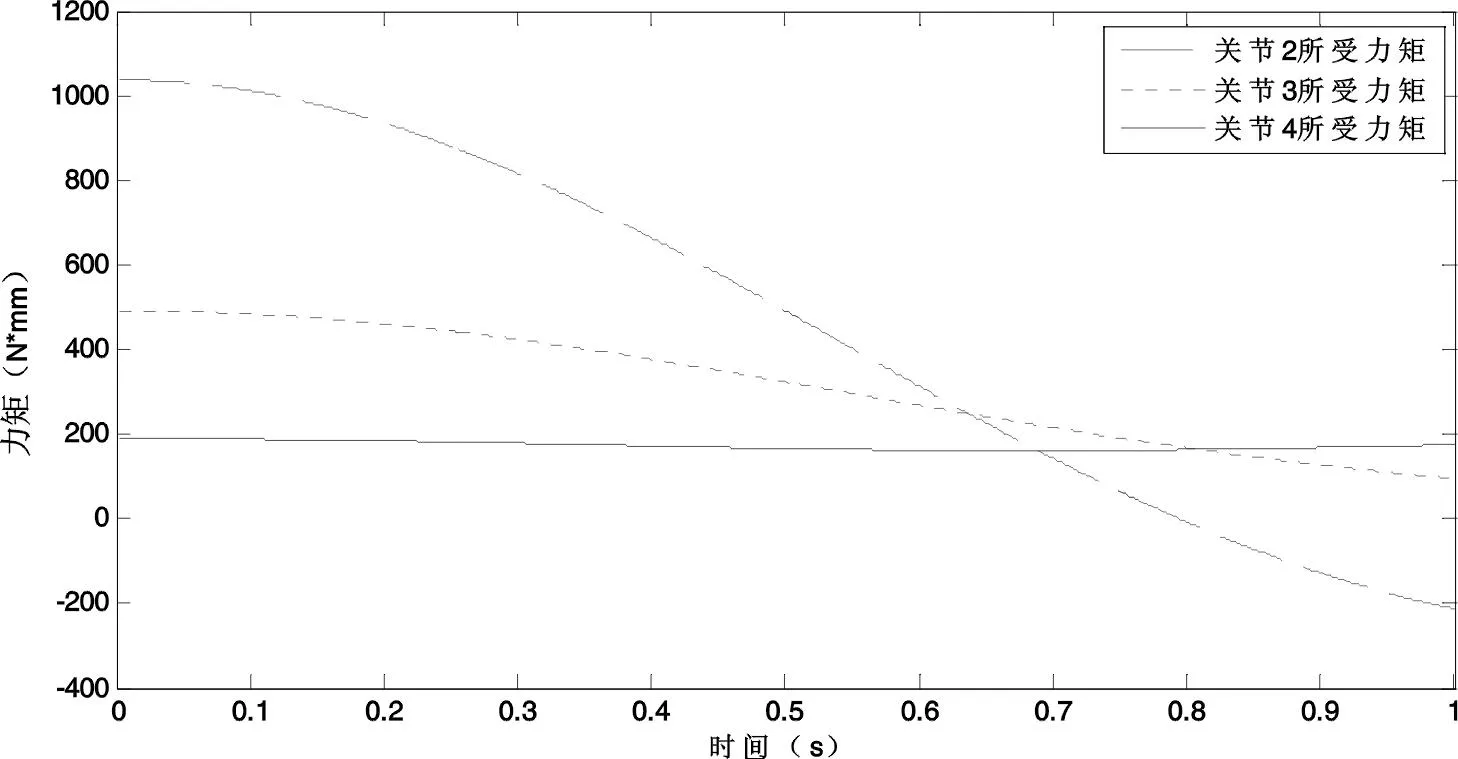
图7　指尖施加5 N外力时关节2、3、4所受力矩

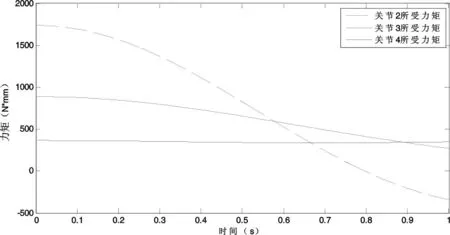
图8　指尖施加10 N外力时关节2、3、4所受力矩

4结语

本文采用DH模型对灵巧手手指运动学方程进行分析和讨论，以便了解灵巧手的关节位置和姿态之间的关系，为下一步研究灵巧手的抓取规划和抓取控制提供依据和打下基础.另外，本文构建了灵巧手的动力学模型，并进行动力学模型的分析和仿真.经过对灵巧手的动力学仿真，对每个关节的驱动力矩进行分析，可以为三指灵巧手控制研究提供依据.

[参考文献]

[1]裴九芳,陈玉,许德章.基于方向可操作度的机器人灵巧手抓持优化研究[J].机械设计, 2012(4):12-16.

[2]郑显华,刘新华,张霖,等.基于Adams的仿人机械灵巧手动力学仿真分析研究[J].制造业自动化, 2013

(7):147-149.

[3]LUHJYS,WALKERMW,PAULRPC.Onlinecomputationalschemeformechanicalmanipulators[J].ASMEJournalofDynamicSystems,MeasurementandControl,1980(2):69-76.

[4]DENAVITJ,HARTENBERGRS.Akinematicnotationforlower-pairmechanismsbasedonmatrices[J].ASMEJournalofAppledMechanics,1955(23):215-221.

[5]余麟,刘昊,彭光正.五指仿人灵巧手运动学与动力学模型[J].北京理工大学学报,2008,28(10):880-884.

[6]王华,孟庆鑫,王立权.基于切片理论的水下灵巧手手指动力学分析[J].机器人,2007,29(2):160-166.

[7]李立全,庞永刚.空间五自由度机械手动力学的研究及仿真[J].机械设计与制造,2009(9):150-151.

[8]CHANJC,LIUY.Dynamicsimulationofmulti-fingeredrobothandsbasedonaunifiedmode[J].RoboticsandAutonomousSystems，2000,32(2):185-201.

[9]杨志明.基于ADAMS虚拟样机的智能仿生手控制研究[D].长春:吉林大学通信工程学院,2014:17-29.

[10]李欢.果蔬采摘机器人末端执行器的设计与研究[D].沈阳：沈阳工业大学,2015:30-41.

[11]钱少明,王志恒,杨庆华.基于气动柔性驱动器的三自由度手指指端输出力特性研究[J].中国机械工程,2014(11):1438-1442.

[12]杨文珍,梁春辉,陈文华,等.ZSTU拟人灵巧手设计与仿真[J].系统仿真学报，2011(12):2617-2622.

(责任编辑穆刚)

Study on kinematics and dynamics simulation of three-fingered dexterous hand

CHEN Yu, XIA Fayin

(Institute of Mechanical and Automotive Engineering, Anhui Polytechnic University, Wuhu Anhui 24100, China)

Abstract：Imitating the structure and function of human hands, the mechanical structure of three-fingered dexterous hand were designed, the dexterous hand joints driven by motor, the structure of the finger being close to the real hand, and every finger have four degrees of freedom. Through the analysis the single fingered kinematics, the coordinate transformation matrix was obtained, and the single fingered position and fingertip displacement were simulated by Adams software; through the dynamics analysis of the dexterous hand, the Adams software was used for dynamic simulation of the common action of single finger bend. The simulation results show that structure design of dexterous hand is reasonable, with large work space, flexible dexterous hand movements, which can realize many kinds of nimble operation.

Key words：dexterous hand; kinematics; Adams simulation; dynamics

[中图分类号]TP241

[文献标志码]A

[文章编号]1673-8004(2016)02-0079-05

[作者简介]陈玉(1973—)，男，安徽怀宁人，副教授，硕士，主要从事机械灵巧手、机电一体化方面的研究.

[基金项目]安徽省自然科学基金项目(1308085ME78)：水压驱动水下灵巧手自主作业规划研究.

[收稿日期]2015-11-09