一个超混沌Lorenz系统的Hopf分岔分析

刘　畅, 张　莉, 秦　爽

(1. 信阳职业技术学院, 河南　信阳　464000; 2.兰州工业学院基础学科部, 甘肃　兰州　730050;

3.兰州交通大学数理学院, 甘肃　兰州　730070)



一个超混沌Lorenz系统的Hopf分岔分析

刘畅1, 张莉2, 秦爽3

(1. 信阳职业技术学院, 河南信阳464000; 2.兰州工业学院基础学科部, 甘肃兰州730050;

3.兰州交通大学数理学院, 甘肃兰州730070)

[摘要]分析了一个超混沌Lorenz系统,并且对其平衡点的局部稳定性和Hopf分岔的存在性进行研究，通过非线性动力学理论研究该系统Hopf分岔周期解的稳定性；最后通过计算机仿真证明理论分析的正确性.

[关键词]超混沌系统;Lyapunov指数;Hopf分岔;范式理论

自上个世纪Lorenz在一个三维自治系统中发现混沌吸引子以后[1],在研究混沌理论及其应用的过程中,混沌理论的研究价值及其他的应用价值不断被学者们所认识,对混沌系统运动研究的关注越来越多.伴随着科学技术的发展以及对混沌理论的逐步深入研究以及工程实际的需要,学者们相继提出各种各样的非线性混沌系统.袁地[2]构造了一个不同于Lorenz系统和Chen系统的三维连续自治混沌系统,并且对系统在不同参数时所产生的复杂动力学现象进行分析.刘俊红[3]讨论了一类新型混沌动力学系统的自适应控制及同步问题,实现了在不同初值且参数未知情况下的自适应同步.高智中[4]构造了一个新的四维超混沌系统,并用数值模拟方法研究该系统的相图、分岔图、Lyapunov 指数谱等动力学行为. 文献[5]设计了一个二次非线性控制器,可以把具有潜在威胁的亚临界Hopf分岔转化成为超临界Hopf分岔. 文献[6]通过Washout-filter方法设计了一个Hopf分岔状态反馈控制器,在保持平衡点不变的情况下,使得非线性系统在期望的参数值处将原来发生的亚临界Hopf分岔转化为超临界Hopf分岔,并且保证了系统在参数值范围内是渐近稳定的. 杜文举等[7]基于Washout滤波器对一类Vander Pol-Duffing系统设计了状态反馈控制器，研究了控制增益对Hopf分岔的存在性及其极限环幅值的影响. Dang等[8]提出了一个超混沌Lorenz系统，设计了两类非线性控制器实现了该系统的同步,并且根据Lyapunov稳定性理论证明了系统的全局渐进稳定性.但文献[8]并没有系统研究Hopf分岔.本文运用中心流行理论和范式理论，更进一步对系统的Hopf分岔行为进行研究.

1新的四维混沌系统

本文主要研究一个新的四维混沌系统[8].该系统的状态方程如下：

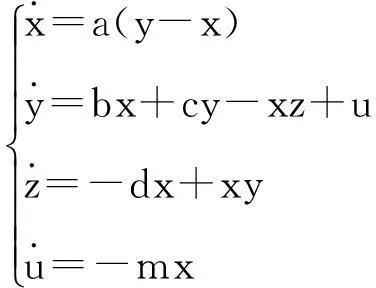
(1)

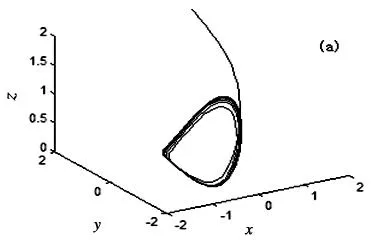
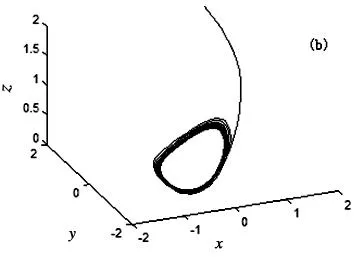
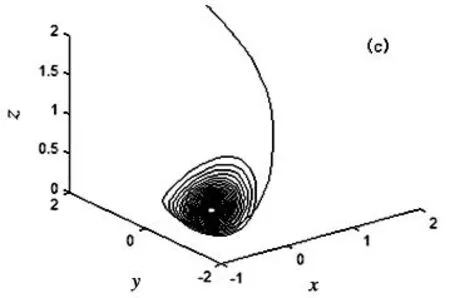
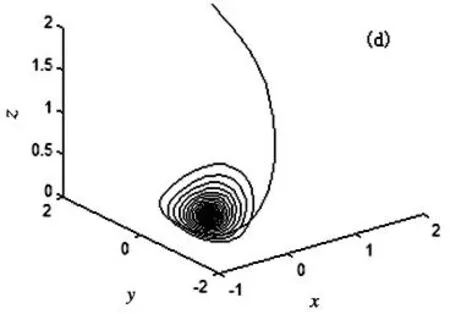
其中x=(x,y,z,u)Τ∈R4是系统的状态变量,a,b,c,m为实参数.当参数a=35,b=7,c=12,d=3,m=5时,系统(1)存在一个混沌吸引子,如图1(a)所示.此时，系统(1)的时间响应图、庞加莱截面图、Lyapunov指数谱图，如图1 (b)、图1(c)和图1(d)所示.

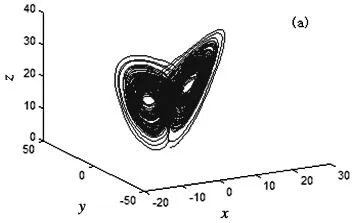
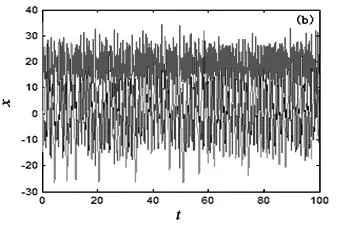
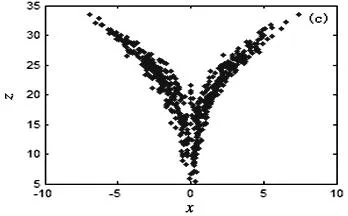
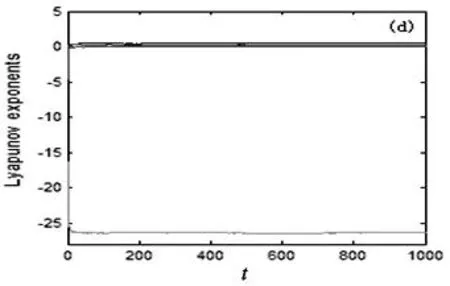
图1　(a) 三维空间吸引子图;(b)系统时间响应图;

2平衡点分析和Hopf分岔的存在性

令方程组(1)的右边等于零，则有

a(y-x)=0,bx+cy-xz+u=0,

-dx+xy=0,-mx=0.

(2)

可以解得系统有唯一的平衡点E0=(0,0,0,0).

系统(1)在E0=(0,0,0,0)的Jacobian矩阵为

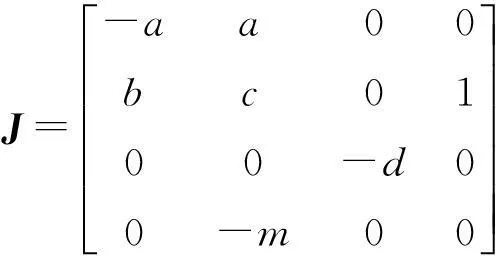
(3)

所以,求得系统(1)在平衡点E0处Jacobian矩阵的特征方程为

f(λ)=(λ+d)[λ3+(a-c)λ2+

(m-ab-ac)λ+am]=0

(4)

根据Routh-Hurwitz判据, 知方程(4)的一切根的实部为负数的充要条件是不等式

d>0,a>c,am>0,m-a(b+c)>0,

(a-c)(m-ab-ac)>am

成立.所以,当满足以上条件时,平衡点E0渐近稳定.

令λ=iω(ω>0)为方程(4)的根,则有

-iω3-(a-c)ω2+(m-ab-ac)iω+am=0

分离以上方程的实部和虚部可得

以及方程(4)的4个特征值为

λ1，2=±iω0,λ3=-d,λ4=c-a.

对方程(4)两边同时关于m求导,有

(5)

根据上式可得

根据Hopf定理[8],可知m0便是分岔的临界值. 当mm0时,有极限环出现.综上所述,系统(1)发生局部的Hopf分岔.假设a>0,b>0,c<0,m>0,a+c>0,当m穿过临界值m0时,系统(1)在平衡点E0处发生Hopf分岔.

3周期解的方向及其稳定性

以下利用Hassard等在文献[9]中提到的范式理论,对系统(1)Hopf分岔所分支出的周期解的方向及其稳定性做进一步研究.通过计算可以得出

Jυ1=iω0υ1,Jυ3=-dυ3,Jυ4=(c-a)υ4

的特征向量

对系统(1)定义如下矩阵

P=(Reυ1,-lmυ1,υ3,υ4)

和变换

(x1,y1,z1,u1)T=P(x2,y2,z2,u2)T

从而有

(6)

其中，

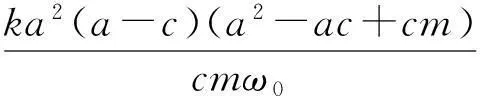
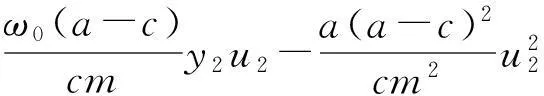
F4(x2,y2,z2,u2)=-kmc(a-c)x2z2+ka(a-c)2u2z2,

k1=ak(a-c)[(a-c)(b+c-1)+m],

k2=ω0k[(a-c)3+ma],

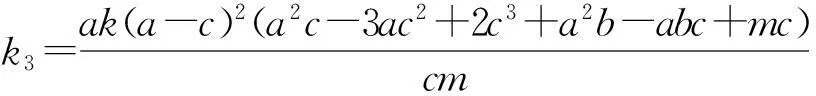
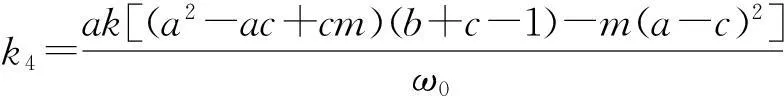
k5=k(a3-2a2c+ac2-a2+2ac-c3),

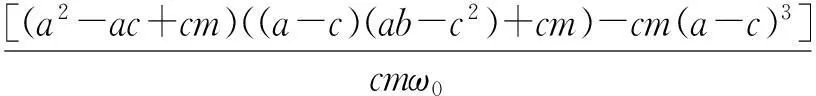
k7=-kmc[m+(a-c)(b+c-1)],

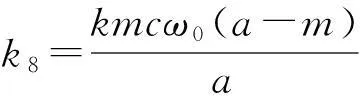
k9=k(a-c)[(a-c)(a2-ac)+a-ab+c2+2mc],

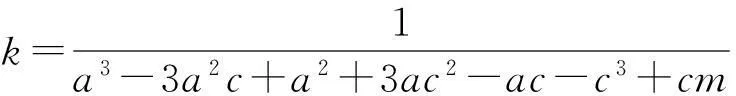
应用Hassard等在文献[9]中提出的方法,进而我们有

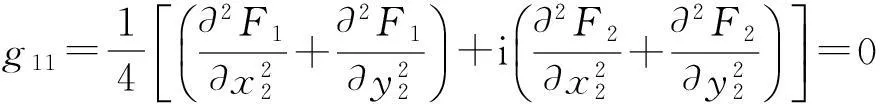
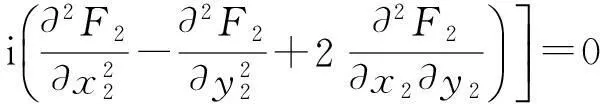
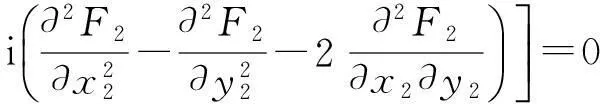
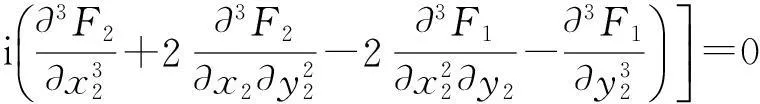
通过解方程

Dw11=-h11,(D-2iω0I)w20=-h20,

可得

其中，

基于上面的分析和计算可得

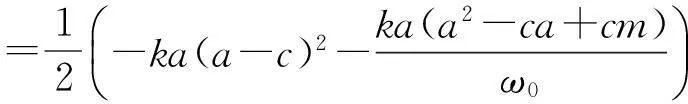
=0,

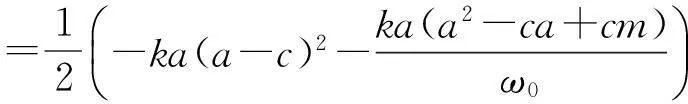
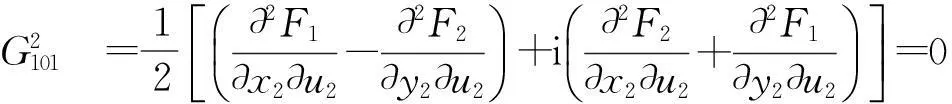
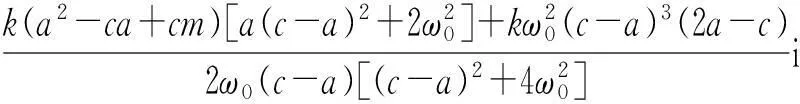
因此,可以得到下面的表达式

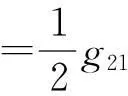
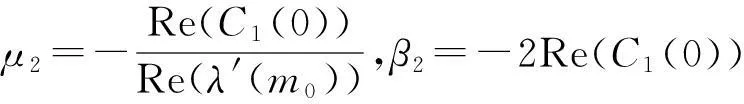
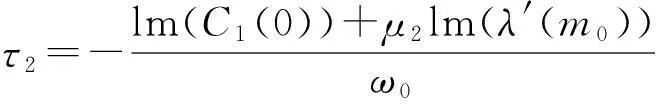
μ2决定Hopf分岔的方向:当μ2>0(μ2<0)时,Hopf分岔是亚临界的(超临界的),并且如果m>m0(m0)时,周期解在中心流形上是稳定的(不稳定的).τ2决定周期解的周期:如果τ2>0(τ2<0),则周期是递增的(递减的).因为当a>0,b>0,c<0时,则有Re(λ′(m0))>0.因此,如果Re(C1(0))>0(Re(C1(0))<0),则系统(1)在平衡点E0的Hopf分岔是超临界的(亚临界的),并且周期解在中心流形上是稳定的(不稳定的).

4数值仿真

为了验证以上理论分析,选取一组参数:a=3,b=2,c=-1,d=3.可以通过计算得出Hopf的临界值m0=12. 当m>m0时,则平衡点是稳定的; 当m0,τ2=-0.068 593<0, 则系统(1)在平衡点E0的Hopf分岔是超临界的,当m

图2　当(a,b,c,d)=(3,2,-1,3)时的平衡点稳定情况：

5结论

本文对一类超混沌Lorenz系统的Hopf分岔行为进行研究，通过理论分析对系统平衡点的稳定性进行研究，选取适当的分岔参数证明了系统Hopf的存在性，而且进一步分析了Hopf分岔周

期解的方向及其稳定性，并通过计算机仿真给出分岔参数变化时系统的相图，数值仿真和理论分析吻合,证明了理论分析的正确性.

[参考文献]

[1]LORENZEN.Deterministicnonperiodicflow[J].J.AtmosphericSci, 1963, 20: 130-141.

[2]袁地.一个类Lorenz系统的混沌动力学分析[J].安阳师范学院学报,2009(2): 26-30.

[3]刘俊红,杨万利,郑素文.一类新型混沌动力学系统的自适应控制及同步研究[J]. 装甲兵工程学院学报, 2010,24(4):91-94.

[4]高智中.一个新超混沌系统及其线性反馈同步[J].中山大学学报, 2012, 51(6):31-34.

[5]李鹏松, 陈书吉，吕雪，等．单参数电力系统亚临界Hopf分岔控制[J]．吉林大学学报(理学版), 2013,51(4): 618-622.

[6]安袆春,张庆灵,张艳，等.基于Wash-out-filter方法控制非线性系统Hopf分岔[J]．东北大学学报(自然科学版), 2008, 29(10):1318-1384.

[7]党红刚,何万生,郭丽峰. 超混沌Lorenz系统的同步[J]．重庆工学院学报(自然科学版), 2008,22(11):104-106.

[8]杜文举,张建刚,俞建宁,等. 基于Washout滤波器的VanderPol-Duffing系统的Hopf分岔控制[J]．吉林大学学报(理学版)，2014,52(3): 568-574.

[9]HASSARDBD,KAZARINOFFND,WANYH．TheoryandapplicationsofHopfbifurcation[M].London:CambridgeUniversityPress, 1981.

(责任编辑吴强)

Hopf bifurcation analysis of a hyperchaotic lorenz system

LIU Chang1, ZHANG Li2, QIN Shuang3

(1. Xinyang Vocational & Technical College, Xinyang He’nan 464000, China;2. Basic Courses Department， Lanzhou Institute of Technology, Lanzhou Gansu 730050, China;3. School of Mathematics and Physics, Lanzhou Jiaotong University, Lanzhou Gansu 730070, China)

Abstract：The paper mainly focuses on the analysis of a hyperchaotic Lorenz system. The local stability of equilibrium is analyzed and existence of Hopf bifurcation is established. The stability of bifurcating periodic solutions is studied by nonlinear dynamic theory. Finally, numerical simulation is given to illustrate the theoretical analysis.

Key words：hyperchaotic system; Lyapunov exponents; Hopf bifurcation; normal form theory

[中图分类号]O415.5

[文献标志码]A

[文章编号]1673-8004(2016)02-0014-05

[通讯作者]秦爽(1992—) , 女，黑龙江大庆人，硕士，主要从事非线性系统动力学及其控制方面的研究.

[作者简介]刘畅(1983—), 女, 河南信阳人，助教,主要从事非线性动力学方面的研究.

[基金项目]国家自然科学基金项目(61364001).

[收稿日期]2015-09-17