多项式分布滞后模型在地面沉降预测中的应用

凌胜任

(苏州工业园区测绘地理信息有限公司，江苏 苏州 215000)



多项式分布滞后模型在地面沉降预测中的应用

凌胜任

(苏州工业园区测绘地理信息有限公司，江苏 苏州 215000)

摘要：介绍多项式分布滞后模型(PDL模型)建立过程，针对地面沉降相对于地下水水位变化的滞后作用，建立考虑滞后作用的多项式分布滞后预测模型，应用该模型对某地区地面沉降实测数据进行模拟预测，并评价模型各项指标。实例分析表明，PDL模型应用到地面沉降变形趋势具有预测精度高、拟合效果好的特点，可以有效实现地下水水位变化导致地面滞后性沉降的定量模拟和预测。

关键词：PDL模型；地面沉降预测；地下水水位；滞后作用

地面沉降是指区域性地面标高降低的一种环境地质变化，是全球范围内普遍存在的问题，其沉降幅度不断加大、影响范围不断扩大趋势[1,2]。在工程建设过程中，地面沉降导致的事故层出不穷，影响形式表现为造成建筑的差异沉降、城市道路的开裂及地下隧道管线的损坏等[3,4]。因此，地面沉降的准确预测，及时提供沉降报警信息对减灾防灾和指导地区工程建设具有重要的意义。

地面沉降的诱发因素主要分为人为因素和天然因素。天然因素主要包括软土层的自重固结、火山运动及地震的冲击等，人为因素主要有抽取地下水、地表施加荷载及各种地下工程建设等[5,6]。本文基于PDL模型对某地区地面沉降数据进行预测，重点考虑地下水对地面沉降量的影响，其思想是地面沉降量受到自身发展趋势影响的同时受到地下水的影响并分布到多个时段。

1模型建立

1.1PDL模型定义

PDL模型是一种动态的回归分析模型，不仅考虑因变量本身滞后项的影响关系，还加入自变量跨时段对其的影响，集合回归模型和时间序列模型的优点，是一种解释能力较强的预测模型[7,8]，其表达形式：

(1)

式中:yt为因变量；yt-i为因变量的滞后项；xt-j为自变量的滞后项；μt为随机扰动项；c为常数；αi,βj分别为因变量滞后项的系数和自变量滞后项的参数；t为时刻；i,j为滞后量；m,n分别为因变量和自变量的滞后期数。

模型中可以只存在一个自变量，也可以存在多个自变量，而滞后期长度可以是有限项也可以是无限项，具体根据地面沉降滞后理论认识与自变量对因变量的解释能力确定，选择对因变量影响较大的滞后项[9]。

1.2模型建立

地面沉降影响因素具有复杂性、多变性，其性质及形式也是多种多样的，且不同因素引起的地面沉降速度、范围和持续时间不同，因此影响因素的择取十分重要。本文在分析建模过程中重点考虑地下水对地面沉降量的影响，经大量的研究表明，地面沉降量与地下水水位变化幅度呈正相关，分布范围与区域地下水降落漏斗基本保持一致，而且地面沉降的产生和发展过程往往与地下水的开采过程保持一致或存在时间滞后，其相应的PDL模型为

(2)

式中:Yt为地面沉降预测值；Yt-i为地面沉降量过去一系列历史值；Ht-j为地下水水位时间序列；αi是地面沉降量自身滞后项的参数；βj是地下水水位影响因子的参数；m为地面沉降量滞后期数；n为地下水水位滞后期数。

1.3滞后期数的确定

采用PDL模型进行地面沉降预测时，首先要利用样本数据确定模型各影响因子的滞后期数。在理论上大致决定模型右端包含的滞后期数，然而在许多情况下，仅从理论上不能完全确定模型滞后期数，这时，必须研究样本数据，从而得到合理的滞后期数，可以采用常用的统计检验来确定[10-12]。

(3)

式中:RSS为残差平方和；TSS为总离差平方和；n为样本容量；k为自变量个数；R2为决定系数。

2)赤池信息准则(Akaike Information Criterion)和施瓦茨准则(Schwartz Criterion)。进行模型选择时，可以通过AIC准则和SC准则确定模型滞后分布的长度，即滞后期数，AIC和SC准则表达式如下：

(4)

(5)

式中：RSS为残差平方和；n为样本容量；k为自变量的个数。

在确定PDL模型滞后期数的过程中，可以通过添加滞后项直至AIC和SC不再降低为止确定滞后的结构。

1.4参数估计

根据代数中的韦亚斯特拉斯(weierstress)定理，PDL模型中参数可用一个适当高次的多项式来逼近。运用该多项式可以有效减小模型待估参数的个数、避免可能存在的高度共线性以及削弱参数估计中的自由度损失。为此，可将式(2)中模型参数βj用一个关于j的多项式来表述，将βj分解为

(6)

在实际运用中，多项式次数p通常取2或3，一般不超过4，本文取p=2，同理将模型参数αi分解为αi=a0+a1i+a2i2,i=1,2,…,m，将分解后的模型参数αi和βj代入式(2)，模型变为

(7)

其中

采用最小二乘法对式(7)进行估计，将估计的参数代入式(6)得到模型参数βj(j=0,1,2,…,n)，同理得到αi(i=1,2,…,m)，最后将αi,βj代入式(2)即可得到所需的PDL模型。

2工程实例及模型评价

2.1工程实例

利用PDL模型对地面沉降进行预测，实验数据来自某地区1984年到2006年连续23年内的地面沉降量及地下水水位(水位面高程)统计数据，如图1所示。

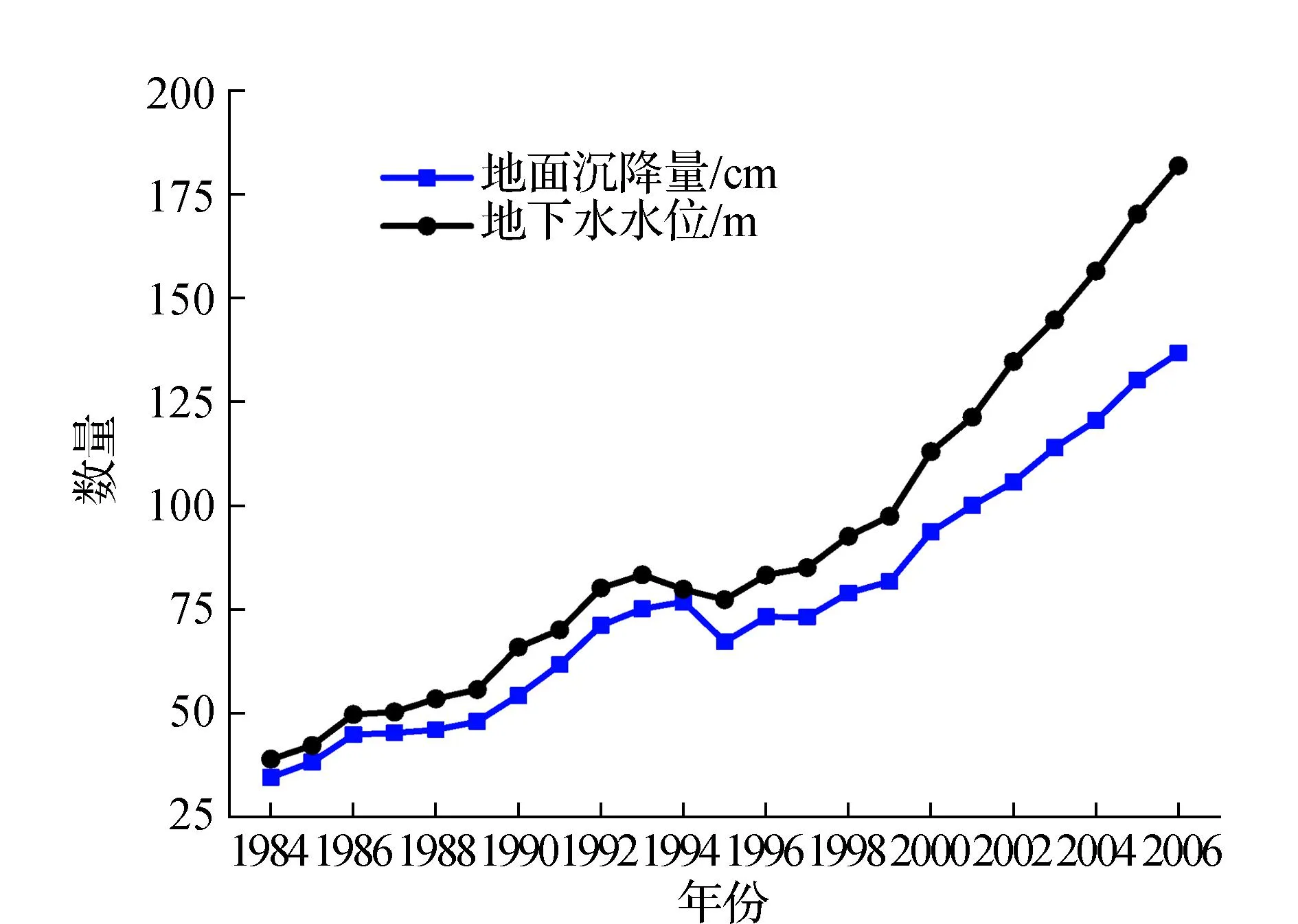
图1　某地区连续23年地面沉降量及地下水水位统计数据

分别用Y和H表示地面沉降量和地下水水位数据，对Y和H两个时间序列分别取对数，因为取对数后可有效减弱变量异常值及随机误差异方差性对模型的影响，并可使模型参数变为弹性。根据上述滞后期数的确定原则以及综合考虑各方面的影响因素，选取地面沉降自身滞后期数m=3，地下水水位滞后期数n=3。对lnY和lnH两时间序列统计数据建立PDL模型，其表达式如下

lnYt=0.031+0.569lnYt-1+0.348lnYt-2-

0.022lnYt-3+0.863lnHt-0.194lnHt-1-

0.524lnHt-2-0.129lnHt-3.

(8)

2.2模型评价

表1　PDL模型各项评价指标

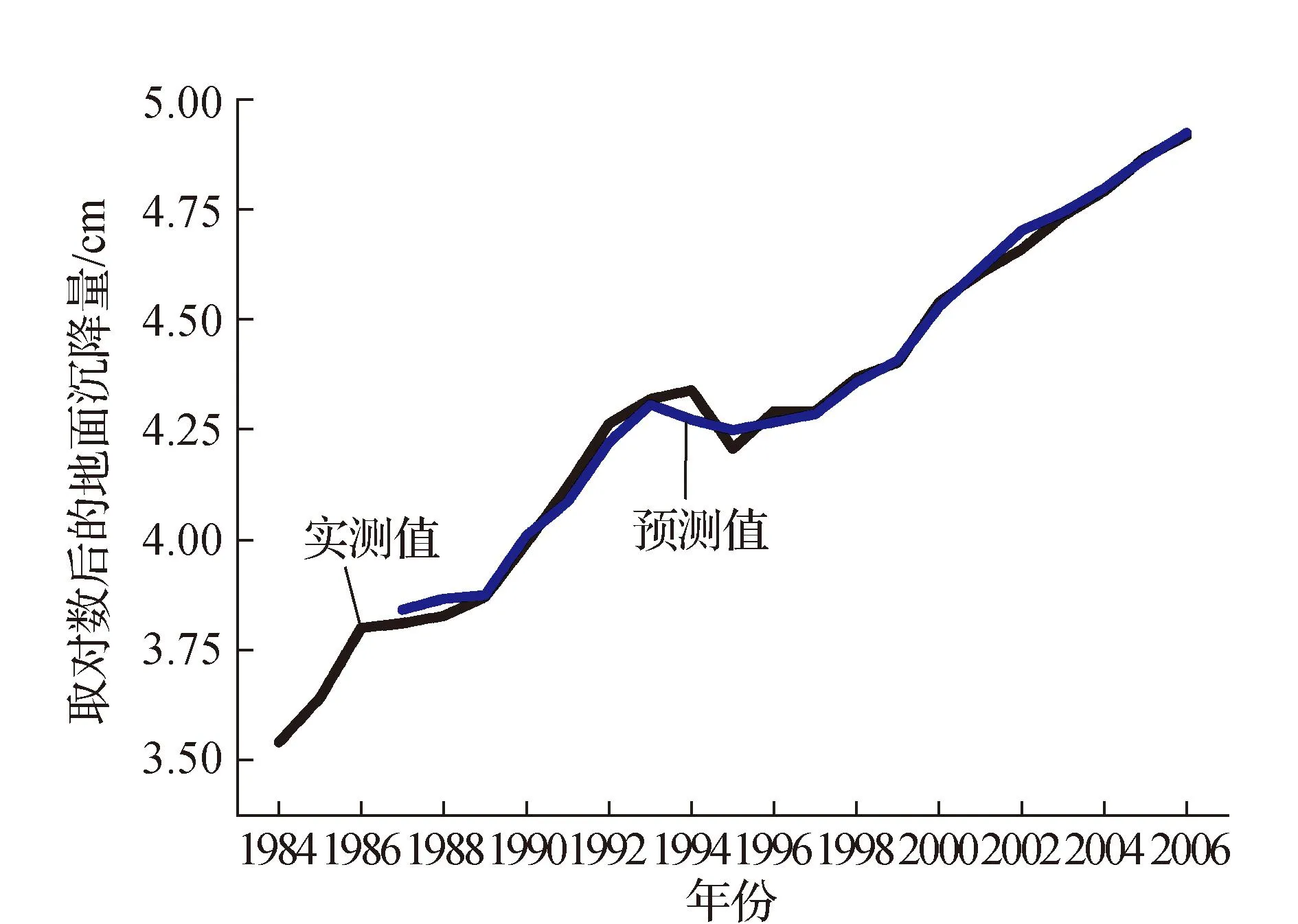
图2　模型预测值与实测值对比

对PDL模型做预测分析，其各项预测指标如表2所示，均方根误差RMSE和平均绝对误差MAE由因变量规模决定，被作为相对指标来比较相同序列在不同模型中的预测结果，误差越小，该模型的预测能力越强，本文RMSE和MAE均较小；平均绝对百分误差MAPE和希尔不等系数TIC统计值是相对量，一般认为0

表2 PDL模型预测分析结果

列实际值的偏差程度，方差率VP反映预测方差与序列实际方差的偏离程度，协方差率CP反映非系统误差的大小，预测结果较好的模型，那么偏差率和方差率应该较小，协方差率较大。本文BP和VP较小，CP较大，符合指标且表明预测效果较好。

3结语

PDL模型集合时间序列模型和回归模型的优点，考虑因变量自身滞后项以及自变量跨时段对其的影响，是一种解释能力较强的预测模型。针对地面沉降相对于地下水水位变化存在时间滞后，建立PDL模型，并采用该模型对某地区地面沉降进行模型预测，结果表明，PDL模型应用到地下水水位变化引起的地面沉降模拟和预测是可行的，并且PDL模型拟合效果良好，预测精度较高，可以有效反映研究区域的地面沉降态势。

参考文献：

[1]张文翔,瞿成松,刘毅,等.灰色模型在基坑工程地面沉降预测中的应用[C]//隧道工程股份有限公司.地下交通工程与工程安全：第五届中国国际隧道工程研讨会文集.上海：同济大学出版社，2011.

[2]程晨.灰色理论和多项式拟合在地表沉降监测中的应用[J].测绘与空间地理信息，2014，37(2)：220-222.

[3]周志广,姚文生,谢轶,等.基于灰色理论的时间序列分析在地面沉降预测中的应用[J].地质灾害与环境保护,2012(4):52-57.

[4]吴蓉,李成柱.基于Preisach滞后模型的地面沉降预测分析[J].水文地质工程地质,2013(6):98-100.

[5]张松,田林亚.时间序列分析在地铁沉降监测中的应用[J].测绘工程,2014,23(10):63-66.

[6]岳建平,方露.城市地面沉降监控理论与技术[M].北京：科学出版社,2012.

[7]楚彬,范东明.改进的多元线性回归模型及其应用[J].测绘工程,2014，23(6):63-66.

[8]谢军,吴伟,杨晓光.用于短时交通流预测的多项式分布滞后模型[J].同济大学学报(自然科学版),2011(9):1297-1302.

[9]冯羽,马凤山,魏爱华,等.考虑滞后作用的地面沉降阿尔蒙分布预测模型[J].中国地质灾害与防治学报,2011(4):117-121.

[10] 丁俊君,戴生泉.多项式分布滞后模型阶数的确定及其应用[J].统计与决策,2004(10):28-29.

[11] 王强，崔希民，张恒璟，等.多项式拟合模型在GPS水准测量中的应用[J].测绘工程，2014,23(8)：19-22.

[12] 丁刚,赵萍萍.基于PDL模型的城市化水平预测[J].统计研究,2005(3):45-48.

[责任编辑：李铭娜]

A PDL model used for the prediction of ground subsidence

LING Shengren

(Suzhou Industrial Park Surveying,Mapping and Geoinformation Co.,Ltd.,Suzhou 215000,China)

Abstract：The process of establishing polynomial distributed lag model (PDL model) is introduced.According to the ground subsidence it shows a nature of hysteresis effect comparing with the fluctuation of groundwater level,and the polynomial distribution lag prediction model is established,which is used to simulate and forecast the ground subsidence based on the measured data of a certain area.The index of the model is evaluated.Example analysis shows the PDL model used to forecast the trend of settlement deformation has the characteristics of high forecast precision and good fitting effect.The quantitative simulation and prediction of the lag of ground subsidence caused by the fluctuation of groundwater level are implemented efficiently.

Key words：PDL model；ground subsidence prediction；groundwater level；hysteresis effect

中图分类号：TU196

文献标识码：A

文章编号：1006-7949(2016)03-0064-04

作者简介：凌胜任(1986-)，男，助理工程师.

收稿日期：2014-12-15