海洋测深网系统误差的平差计算

许运鹏，高　昂，孙　磊，吕玉婷

(1.中国地质大学 信息工程学院，湖北 武汉 430074；2.河南省遥感测绘院，河南 郑州 450003)



海洋测深网系统误差的平差计算

许运鹏1,2，高昂1，孙磊2，吕玉婷1

(1.中国地质大学 信息工程学院，湖北 武汉 430074；2.河南省遥感测绘院，河南 郑州 450003)

摘要：利用一般多项式模型、线性多项式与三角函数多项式结合的模型，将系统误差表示为与时间相关的量，对海洋测深网的系统误差值进行分离。引入半参数模型，将参数值与模型误差进行分离；结合实测的交叉点不符值进行平差计算，使平差后精度进一步提高。

关键词：海洋测深；系统误差；交叉点不符值；半参数模型

测深数据误差处理的研究大多集中在异常值的剔除方面，国内外的学者在异常值的剔除方面做较多研究[1-4]。然而，存在一个突出问题就是如何准确探测可能存在的系统误差及准确评估测深精度。黄谟涛提出基于交叉点差值的海洋重力测线半系统差探测及误差补偿等方法[5]，李明叁对基于秩亏网的海洋测深网的平差模型进行研究[6]。传统的海洋测深系统误差的分离模型均将一条测线上的系统误差认为是一个定值，由于测深船只在航行的过程中受到种种不稳定因素的干扰，所获得的测深数据表现出与时间相关的特性。因此本文将航空重力测线网平差中的一般多项式模型和线性多项式与三角函数多项式结合的模型(下文中简称三角多项式模型)引入到海洋测深网系统误差的平差之中[7]，并利用半参数模型进行模型误差的分离，最后结合实例验证将各测线上的系统误差表示为与时间相关的量，使得测深成果的精度得到较大提高。

1海洋测深网的系统误差分离模型

传统海洋测深中常假设一条测线上各测点的系统误差是一个定值，可以通过交叉点的不符值反映出来，通过对交叉点不符值进行平差处理计算出各条测线的系统误差。

(1)

(2)

(3)

在海洋测线网平差中，传统的系统误差分离模型对于那些含有定值的系统误差可以较好的计算出来。然而在实际的测量中，由于海洋测深的影响因素比较多，一条测线各点的系统误差往往表现出与时间相关的特性，可以采用一般多项式与三角多项式模型，两种模型表示为

(4)

(5)

式中：t为观测时刻，ω代表对应于误差变化周期的角频率，一般取ω=2π/T(T表示整条主、副测线的观测时间)，三角多项式由两部分组成，分别表征误差综合影响的线性变化规律和误差影响的复杂变化规律。

误差模型可以表示为

(6)

其中,Si(tij),Sj(tji)为第i条主测线与第j条检查测线在tij与tji时刻的系统误差值。

可以写出误差方程的矩阵形式：

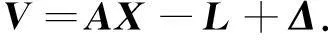
(7)

其中，A为由1，-1，0，tij，tji，-tij,-tji构成的系数矩阵;L为交叉点不符值向量。

由最小二乘原理解得

(8)

为保证尽可能全面的补偿系统误差，如果将所有测线参与平差，系统误差的模型参数太多，其中的一些附加参数对平差结果影响很小，如果误差模型把这样一些参数都包含进来，不但计算量大，而且还会导致计算精度下降，因此有必要对所有测线进行系统误差的显著性检验，只对其中的那些系统误差显著的测线进行系统误差的计算，同时还可以解决法方程秩亏的问题。

引入t检验法检验系统误差，对于每条测线的交叉点不符值来说，其均值应为0，否则该测线的系统误差显著，假定：

国内科研工作者赵钦新[4]等研究了各种常用耐候钢在一定气氛下的硫酸露点腐蚀特性，研究发现不同钢材的腐蚀曲线存在相似的变化趋势，但是转折点有所不同；理想的烟气冷却器装置壁温应高于65℃，且装置材料首选ND钢。

选定显著水平α后，构造统计量：

(9)

其中

2引入半参数模型的海洋测深网系统误差的分离

在实际的测量中，由于海洋测深的环境比较复杂，任何一种平差方法往往都只是模型的近似表达，为了能够有效的分离模型的误差，以半参数模型对其进行平差，可以通过对交叉点不符值平差，将其中的参数值与模型误差分别计算，提高平差结果的精度[8,9]。

(10)

在参数模型最小二乘的基础下，半参数补偿最小二乘准则定义为

(11)

(12)

(13)

组成法方程为

(14)

令S=(P+αR)-1，由法方程可以解得

(15)

(16)

3正则矩阵与平滑因子的确定

3.1正则矩阵R的选取

选取正则矩阵的方法一般有时间序列法、自然样条光滑法以及距离法等。

由于海洋测深网的系统误差分离模型中的观测值(交叉点不符值)表现出与时间相关的特性，因此采用时间序列法确定半参数模型中的正则化矩阵R：

(17)

其中

(18)

3.2平滑因子α的选取

平滑因子α的选取常采用交叉核实与广义交叉核实函数法、L曲线法以及均方误差最小法等。

采用广义交叉核实法来选取平滑因子α，该方法的基本思路是：在满足交叉核实函数为最小的情况下选择光滑因子α，在具体问题中也就是迭代选取平滑因子α以使交叉核实函数值为最小。

令μ1=tr(H(α))/n，则有迭代式：

(19)

其中，H(α)=S+(I-S)A[ATP(I-S)A]-1ATP(I-S)。

4算例分析

数据采用某海区测深的交叉点不符值，选取其中的12条主测线与12条检查测线(横向表示主测线，纵向表示检查测线)构成的测线网，测深仪器由国产的SDH-13D回声测深仪(技术参数：工作频率208 kHZ，设计声速1 460 m/s，测深准确度±0.4%±5 cm，波束角度8°±1°)。该海区的深度范围22~28 m，交叉点不符值如表1所示。

对12条主测线与12条检查测线进行显著性检验的结果如表2和表3所示。

表1　测线的交叉点不符值　m

表2　主测线t检验的结果

表3 检查测线t检验的结果

在显著水平α=0.01，自由度为11的情况下，计算拒绝域：|t|>2.7。

由检验结果可以看出，主测线的系统误差并不显著，检查测线的系统误差比较明显，因此只对检查测线进行系统误差的计算，采用一般多项式模型与三角多项式模型分别进行计算，并结合半参数模型将其模型误差进行分离，各方案系统误差补偿后交叉点不符值统计结果对比如表4所示。

由上述计算可以看出，各种平差方法均可以使得观测网的精度得到较大提高，将一般多项式模型与三角多项式模型引入到海洋测深网平差中，系统误差的补偿效果均得到显著性改善，再进一步结合半参数模型分离模型误差之后，交叉点不符值的精度得到较大提高。

表4　各种平差方法补偿效果的对比　m

为了便于直观，各种平差模型平差改正后的交叉点不符值用圆表示，圆的大小(半径)表示交叉点不符值的大小(图例上列出了不同大小的圆所对应的半径)，圆的实心与空心表示交叉点不符值的正负(其中实心表示交叉点不符值为正值，空心表示为负值，单位:m)，如图1所示。

由以上平差结果可见，将一般多项式模型与三角函数模型引入到海洋测深网平差中，可以提高数据平差后的精度，进一步利用半参数模型分离误差后，使得观测网的精度得到接近一倍的水平。另外，在进行系统误差的改正时，要详细分析测线系统误差与模型误差产生的原因，便改正后的数据更合理。

图1　各平差模型平差后所得交叉点不符值图

5结论

在传统海洋测深秩亏网平差的基础上，通过t检验对其中系统误差明显的测线进行平差可以解决法方程秩亏的问题，引入一般多项式模型或者三角多项式模型可以将交叉点不符值进行较好的改正，进一步利用半参数模型对其中的模型误差进行分离，能够使平差后的精度得到进一步的提高。

参考文献：

[1]阳凡林，郑作亚，郭金运，等.多波束测深的异常数据编辑技术和实现[J].测绘科学，2009，34(6)：79-80.

[2]黄贤源，隋立芬，翟国君，等.遗传算法在海洋测深异常数据处理中的应用[J].测绘科学技术学报，2010，27(4)：248-250.

[3]王海栋.多波束系统测深异常处理理论与方法研究[D].郑州：信息工程大学，2010：21-55.

[4]李明叁，刘雁春，暴景阳,等.海洋测深数据的抗差Kalman滤波[J].测绘科学，2006(31)：28-29.

[5]黄谟涛，翟国君，欧阳永忠，等.海洋重力测量误差补偿两部处理法[J].武汉:武汉大学学报(信息科学版)，2002，19(3)：251-255.

[6]李明叁.海洋测深网平差的理论与方法研究[D].郑州：信息工程大学，2007：18-30.

[7]李海，夏哲仁.航空重力测线网平差[J].测绘研究所学报，22(1)：1-5.

[8]丁士俊.测量数据的建模与半参数估计[D].武汉：武汉大学，2005：25-29.

[9]黄凯.半参数模型精度研究[J].测绘工程，2013，22(3)：13-15.

[10] 潘雄.半参数模型的估计理论及其应用[D].武汉：武汉大学，2005：17-23..

[11] 胡宏昌，孙海燕.正规矩阵R及平滑因子α的选取[J].测绘工程，2003，12(4)：6-8.

[12] 植江瑜,夏林元,夏敬潮.等价观测理论的可变参数序贯平差模型[J].测绘科学，2015，40(5)：125-131.

[13] 刘志平，张书毕，卞和方.经典平差函数模型的概括形式分析[J].测绘工程，2015,24(3)：78-80.

[14] 奉延龙,王建雄.一种优化的自由网平差及其在变形监测中的应用研究[J].测绘与空间地理信息，2015，38(5)：170-172.

[责任编辑：李铭娜]

Adjusting the sounding data’s system error acquired in a grid pattern

XU Yunpeng1,2,GAO Ang1,SUN Lei2,LYU Yuting1

(1.School of Information Engineering,China University of Geosciences,Wuhan 430074,China；2.Remote Sensing and Mapping Institute of Henan Province,Zhengzhou 450003,China)

Abstract：In this paper,using the general polynomial model,linear combination of polynomials and trigonometric polynomial model,it makes the system error correlated with time,then separates the system error from the bathymetry network.And it also uses semiparametric model to separate the parameters and error model.Combined with the measured crossing-error it proves the system error correlated with time is valid.

Key words：bathometry;systematic error;crossover differences;semiparametric model

中图分类号：P229

文献标识码：A

文章编号：1006-7949(2016)03-0021-04

作者简介：许运鹏(1987-)，男，硕士研究生.

基金项目：国家自然科学基金资助项目(41374017)；中央高校基本科研业务费专项资金项目(CUG090110)

收稿日期：2015-01-08；修回日期：2015-07-01