基于故障可观性的输电线路故障定位方法

姜 臻，苗世洪，刘 沛



基于故障可观性的输电线路故障定位方法

姜 臻1，苗世洪2，刘 沛2

(1.广东电网有限责任公司珠海供电局，广东 珠海 519000； 2.强电磁工程与新技术国家重点实验室，华中科技大学，湖北 武汉 430074)

广泛研究的基于WAMS的故障定位算法都基于理想化的量测条件，这使得它们在实际应用中受到限制。为了使电网在信息不全条件下(如极端气候、通信故障等)提供可靠的故障定位方案，提出了一种基于故障可观性的输电线路故障定位方法。该方法采用分布参数输电线路模型，可以更准确地考虑分布电容电流对故障定位精度的影响；算法性能优异，且不受故障初始相位角、负荷及故障路径阻抗的影响；仅需要相量测量单元(PMU)的暂态数据信号，无需系统阻抗等其他信息；算法没有迭代过程，计算速度快。诸多仿真分析验证了该方法的有效性和鲁棒性。

故障定位；故障可观性模型；分布参数；信息不全条件；故障路径阻抗

0 引言

简单、快速、准确的故障定位对输电线路的运行和维护至关重要[1]。它必须做到能减轻现有巡线任务的工作负担，及时发现线路绝缘隐患，加速线路故障排查，协助尽快恢复供电，进而保障电网运行的可靠性，减少因停电造成的经济损失。

许多学者已经提出相关单端、双端、三端及多端的输电线路故障定位算法[2-8]。随着相量测量单元(Phasor Measurement Unit，PMU)技术在电力系统中的飞速发展及成熟应用，许多基于PMU的输电线路故障定位技术也被提出[9-12]。然而，为了达到较高的故障定位精度，这些故障定位算法要求系统所有母线都必须安装PMU，这使得它们在实际应用中受到限制。因此，如何在最少的PMU配置下实现快速、准确的故障定位，从而可为电网在信息不全条件下(如极端气候、通信故障等)提供可靠的故障定位方法已成迫切需要解决的关键问题。

类比电力系统状态可观性概念，故障可观性可以定义如下：当电网发生故障时，该故障可由已安装的PMU准确地定位出，这就说明该电网具有基于PMU量测的故障可观性[13-14]。文献[13]提出了一种基于PMU最优安装策略的新型输电线路故障定位算法，尽管如此，由于该算法需要进行复杂的数值迭代及接地阻抗评估，这使得该算法的实用性和可靠性大大降低。

在现代微机保护中，电网故障距离可以通过测量电压、电流值计算故障阻抗来求取。然而，由于受到分布电容、负荷电流及故障阻抗的影响[15-16]，仅仅通过保护安装处的电压、电流值来求取准确的故障距离是非常困难的。本文在PMU故障可观测性的前提下，提出一种实用的输电线路故障定位方法。该方法具有如下几个特征：① 基于PMU故障可观测性。也就是说，本方法并不需要在所有母线上都安装PMU，它可以实现PMU的最优配置，可以完成电网在状态信息不全条件下的故障定位功能。② 采用分布参数输电线路模型，从而可以更准确地考虑分布电容电流对故障定位精度的影响。③ 算法计算没有迭代过程，计算速度快。④ 只需要PMU的暂态数据信号，无需系统阻抗等其他信息。⑤ 算法性能优异，且不受故障初始相位角、负荷及故障路径阻抗的影响。本方法可以应对各种线路故障，且便于电力系统实际应用。诸多仿真分析验证了该方法的有效性和鲁棒性。

1 故障可观测性分析

相量测量单元(PMU)可以实时测量其所在母线的电压相量和该母线所有进出线的电流相量，同时可以给这些测量量打上同步时标[17-18]，因此可以用来实现在广域范围内的故障定位算法。本文使用了一种间隔母线配置PMU的布点策略：首先将PMU装设在线路一端的母线上，然后在与线路没有配置PMU一端相邻的任一母线上配置一个PMU，如此就可以对与这3个母线中的任2个母线相连的线路实现精确的故障定位。对于故障定位来说，这种PMU布点策略是实现故障可观性PMU配置量最少的布点策略[13]，它为实现电网在信息不全条件下(如极端气候、通信故障等)的故障定位方案提供了保障。根据这一PMU配置策略，任何复杂的电力网络都可以被划分为如图1所示的简化模型。

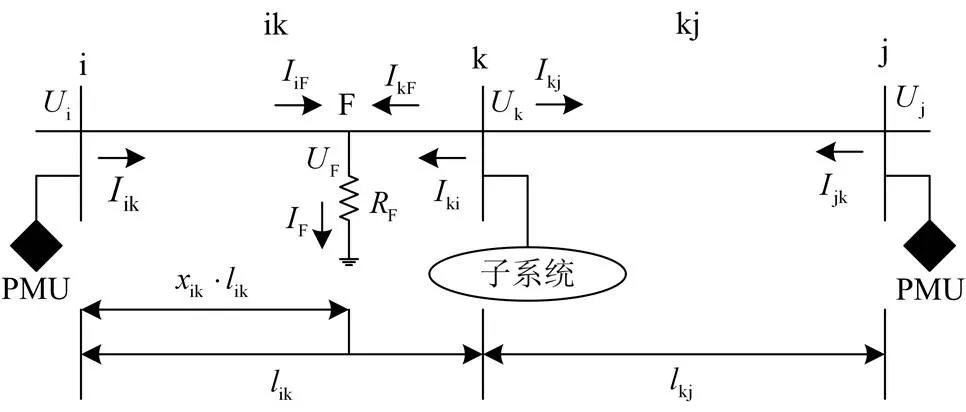
图1 故障条件下输电网络简化模型

如图1所示，仅在母线i和母线j上配置PMU，则母线i、k、j的组合就属于具有故障可观性的PMUs布点策略。图中仅母线k没有配置PMU。子系统表示与母线k相连的其他拓扑，其内部结构不会对算法的结果造成影响。i、k、j分别为母线i、k、j的电压；ik为支路ik上的电流，电流方向由母线i指向母线k，其他电流量的定义类同。假设线路ik之间发生了故障，故障点距离母线i的距离占ik线路全长的百分比为ik。

本文所描述的故障定位方法需要使用PMU测量点的电压和电流量。如表1所示，PMU的相电压、相电流可用于单相接地故障(SLG)的故障定位，而线电压、线电流可用于两相接地故障(DLG)、相间故障(LL)和三相故障的故障定位。

表1 测量分量说明

2 故障定位算法

输电网络简化模型如图1所示。相量测量单元PMU仅安装在母线i和母线j上，连接母线k的子系统对本故障定位算法没有任何影响，因此对该子系统的类型不做任何限制，所以它可以是发电机、负载或是其他复杂的互联系统。母线k到母线i、母线j的距离分别为ik和kj。此外，本故障定位算法使用的是分布参数线路模型。

假设故障发生在线路ik上，如图1所示。尽管母线k上没有安装PMU，但母线的实际电压可以通过母线j上的PMU测量值来推导。其计算公式为

(1)

通过母线i可以计算故障点F的电压、电流信息：

(3)

通过母线k可以计算故障点F的电压、电流信息如下：

(5)

因此，故障路径总电流为

根据式(1)、式(3)、式(5)和式(6)，可推故障路径总电流为

(7)

对电力系统输电线路故障而言，不论经电弧接地还是经大树接地，故障通路都可以认为是纯电阻性的。由此，故障通路电流和故障点电压的相位可以视为相等。此外，这个性质也适用于金属性短路故障，这是因为金属性短路故障点电压为0。因此，线路故障点应满足如下条件：

此外，测量电压、电流的正序、负序和零序分量同样满足式(1)~式(7)，只是相应的波阻抗及传播常数需要对应正、负和零序的参数值。在下文中，正、负和零序分量分别用下标“1”，“2”和“0”区分。为了简化公式表达，现定义：,,及。

当系统发生单相接地故障(SLG)时，如表1所示，测点相电压和相电流将用于故障定位，此时故障路径电流的正序、负序和零序分量之间的关系如下：

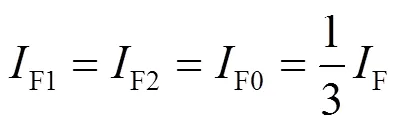
根据式(8)可推：

(10)

其中，

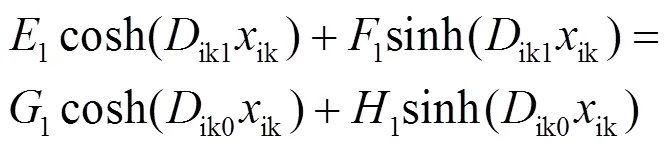
其中，

；

；

。

根据(9)可得：

相应地可以表达如下：

(13)

其中，

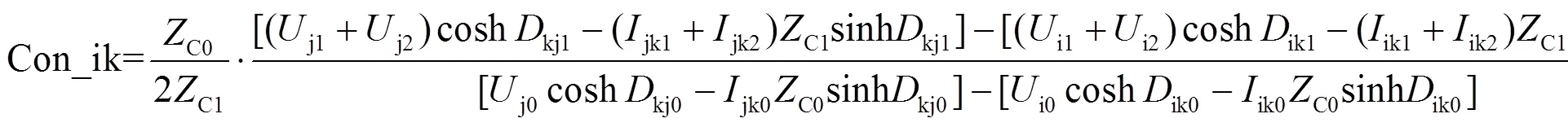
因此，可以得到如下关系：

(14)

其中，

(15)

其中，

，

。

当系统发生相间故障(LL)时，如表1所示，由于相间故障不会产生零序分量，测点线电压和线电流将用于故障定位。此时故障点电压及故障路径电流分别为

(17)

当系统发生两相接地故障(DLG)和三相接地故障时，故障定位可按式(19)进行计算。由于是一个复数，所以式(15)和式(19)的计算结果也应该是一个复数。考虑到的实数部分非常小，所以计算结果的虚数部分几乎为0。因此，的实数部分就可以视为准确的故障发生距离。

3 故障定位计算流程

基于PMU故障可观性配置的新型故障定位方法工作流程如图2所示。PMU和PMU的三相电压、电流测量信号被同步采集，这包括各相电压, 相电流, 各线电压及线电流。其中，各相电压、相电流可根据对称分量变换分解为正、负和零序分量，以便用于故障定位的计算。根据式(16)和式(19)，就可以求得故障距离。同理，也可以求得。

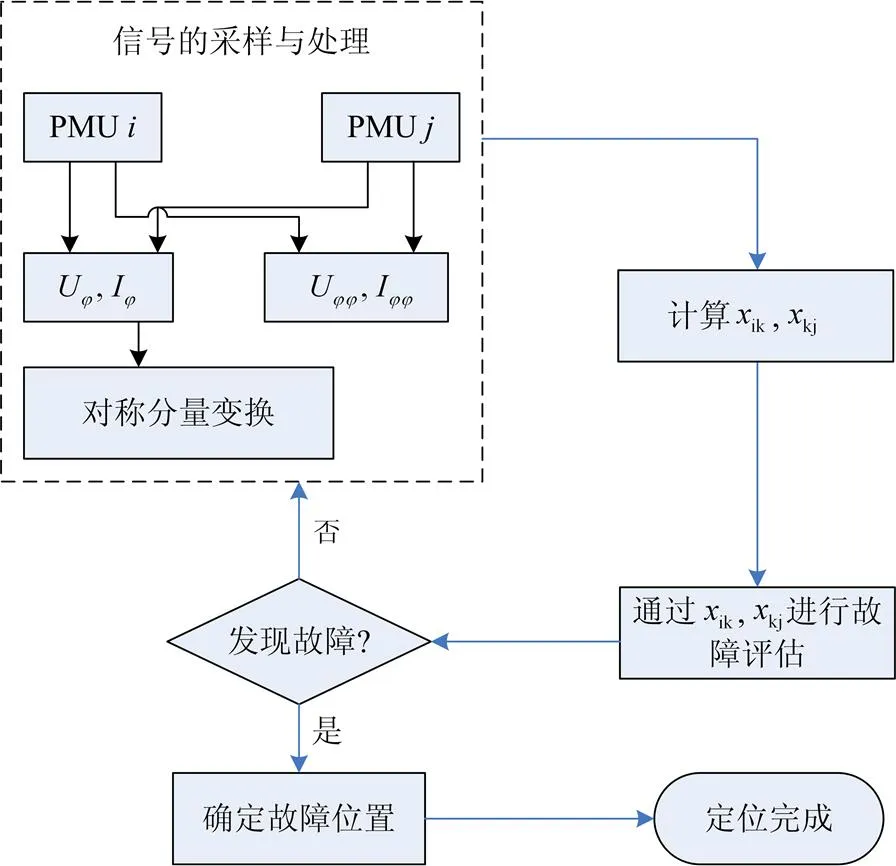
图2 故障定位技术流程图

4 算例分析

4.1 仿真模型

为了验证所提算法的有效性和鲁棒性，本文使用PSCAD/EMTDC仿真平台, 建立了一个经典的500 kV、50 Hz输电系统模型，如图3所示。该模型为两台800 MVA发电机组通过输电线路向大电网(无穷大系统)供电。测量单元PMUs分别安装在母线1和母线3上。相应的仿真简化模型如图4所示。其中，故障分别设置在线路12(母线1到母线2之间的输电线路)、线路23(母线2到母线3之间的输电线路)、母线2、线路13(母线1到母线3之间的输电线路)上。F1，F2和F3可以认为是内部故障，而F4则可认定为外部故障。尽管如此，F4仍然可以通过母线1和母线3上的PMU精确定位出，而且这种基于线路双端PMU的故障定位技术已经十分成熟[2,18]，故而这种情况不在本文研究范围之内。该系统仿真模型的相关参数如图3所示。整个仿真时间为3 s。

图3 仿真系统模型

图4 仿真系统简化模型

故障定位的百分比误差定义如下：

为了验证故障定位方法的相关性能，本文进行了大量的算例分析，这些分析详见以下几个小节。

4.2 故障定位精度评估

为了评估本文故障定位方法的精度，如图3所示的PSCAD/EMTDC仿真系统模型设置了不同类型、通道电阻及发生距离的输电线路故障。在这部分的仿真研究中，故障发生时刻设置为2 s。其中，仿真设置的故障类型包括：A–g(单相接地故障), BC-g(两相接地故障), CA(两相相间故障)和ABC-g(三相接地故障)。仿真结果详见表2~表4，它们分别列出了线路12、线路23和线路13上的故障定位结果，其中表示从母线1到故障点距离占线路12总距离的百分比值，表示从母线2到故障点距离占线路23总距离的百分比值。从表中结果可以看出，本文故障定位方法故障定位的最大误差值仅为2.12%。

现举例说明，如表2所示，两相相间故障(CA相间故障带5 Ω故障通道电阻)发生在线路12上，距离母线10.25 p.u. (35 km)处。在这个算例中，计算值为0.245 4 p.u.，而计算值为-0.735 9 p.u.，因此，正确的故障定位值可以认定为0.245 4 p.u. (34.356 km) ，同时，故障定位误差为0.46%。如表3，两相接地故障(BC两相接地故障带10 Ω故障通道电阻)发生在线路23，距离母线20.8 p.u. (160 km)处。在这个算例中，计算值为3.727 7 p.u.，而计算值为0.790 2 p.u.，因此，正确的故障定位值可以认定为0.790 2 p.u. (158.04 km)，同时，故障定位误差为0.98%。如表2，三相接地故障(ABC三相接地故障)发生在母线2上。在这个算例中，计算值为0.998 8 p.u.，而计算值为-0.001 4 p.u.。由于故障定位误差极小(故障定位的最大误差值仅为2.12%)，所以式(20)中的仅需要设置为一个很小实数即可。在本仿真算例中，设置为0.025。因此，该算例计算值可以认定为故障发生在母线2上。如表4所示，单相接地故障(A单相接地故障带300 Ω故障通道电阻)发生在线路13上，距离母线1 0.9 p.u. (306 km) 处。在这个算例中，计算值为2.414 3 p.u.，而计算值为-3.373 4 p.u.，因此，该算例故障可仍定为外部故障。

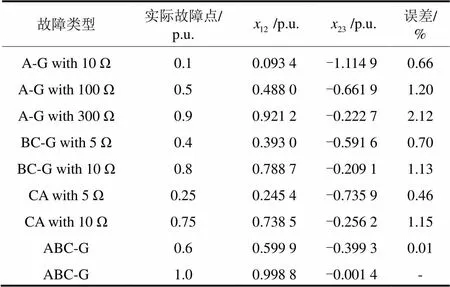
表2 线路12上故障定位精度评估表

表3 线路23上故障定位精度评估表

表4 线路13上故障定位精度评估表(外部故障)

4.3 暂态响应评估

这部分对故障定位方法的暂态响应进行了评估。图5(a)显示的是线路12上距离母线10.25 p.u. (35 km)处CA相间故障(带5 Ω故障电阻)的暂态故障定位轨迹。图5(b)是线路23上距离母线2 0.8 p.u. (160 km)处BC两相接地故障(带10 Ω故障电阻)的暂态故障定位轨迹。图5(c)是母线2上ABC三相接地故障的暂态故障定位轨迹。图5(d)是线路13上距离母线1 0.9 p.u. (306 km)处A相接地故障(带300 Ω故障电阻)的暂态故障定位轨迹。从这些算例可以看出，和是按照不同的轨迹巡行的。故障发生时刻为2 s，从这些暂态响应评估图可以看出，正确的故障定位结果可以在故障发生20 ms后得到。

4.4 故障初始相位角对定位的影响评估

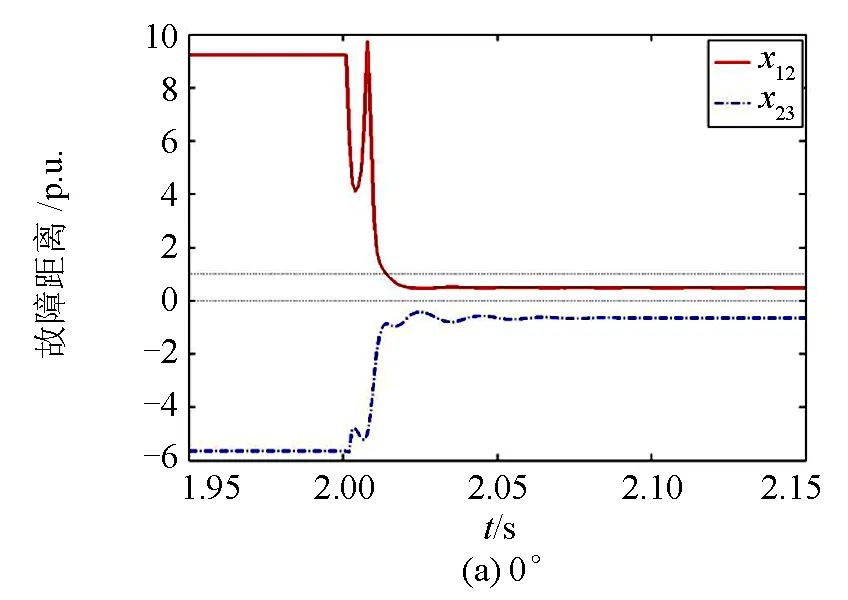
为了验证本文故障定位方法的鲁棒性，考虑电力系统事件的多变性，本小节重点评估故障初始相位角对定位的影响。不同故障初始角的暂态响应轨迹如图6所示。现设置单相接地故障(A相带30 Ω故障电阻)发生在线路12上距离母线10.50 p.u. (70 km)处，并评估6个故障初始相位角的暂态响应，这6个故障初始相位角分别是：0°, 45°, 90°, 135°, 180°和225°(相对于A相电压过零点的相位角度)。结果表明：不同故障初始相位角的故障暂态响应轨迹虽然不同，但它们并不影响最终的故障定位误差。

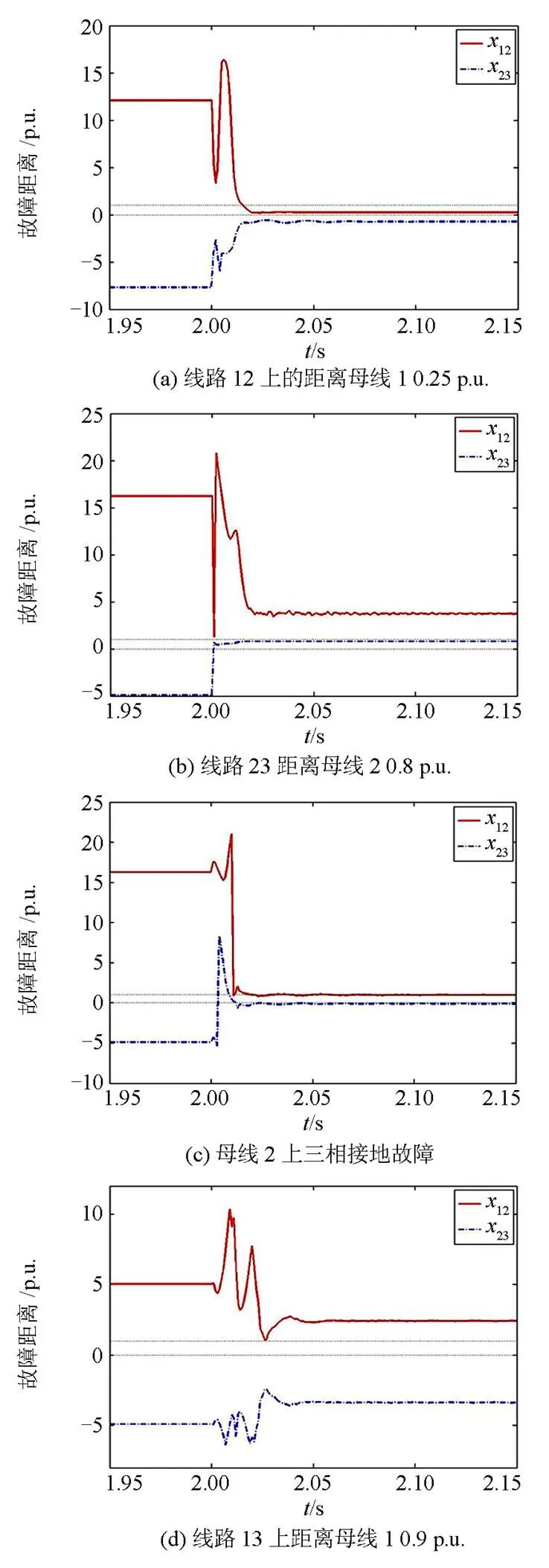
图5 故障定位暂态响应评估

4.5 稳态误差评估

线路12上不同类型故障的定位误差的统计评估如图7所示。从图中可以清晰地看出，当故障发生位置不同时，故障定位误差并没有多少变化，同时在算例中，定位误差没有超过0.6%，定位性能优异。此外，也对不同故障通道电阻下的稳态定位误差进行了对比、分析。图8显示的是线路23上单相接地故障(A相接地)带不同故障通道电阻的稳态定位误差分析。分析结果表明，本文故障定位方法的误差并不会随着故障通道电阻大小的改变而发生较大的变化。当故障通道电阻由0向300 Ω变化时，故障定位误差最大值为2.12%。此外，当故障带较小的通道电阻时，定位误差几乎不变，而这是由于本文故障定位方法算法本身的特征决定的。

4.6 误差来源分析

图7 线路12上不同类型故障的定位误差评估

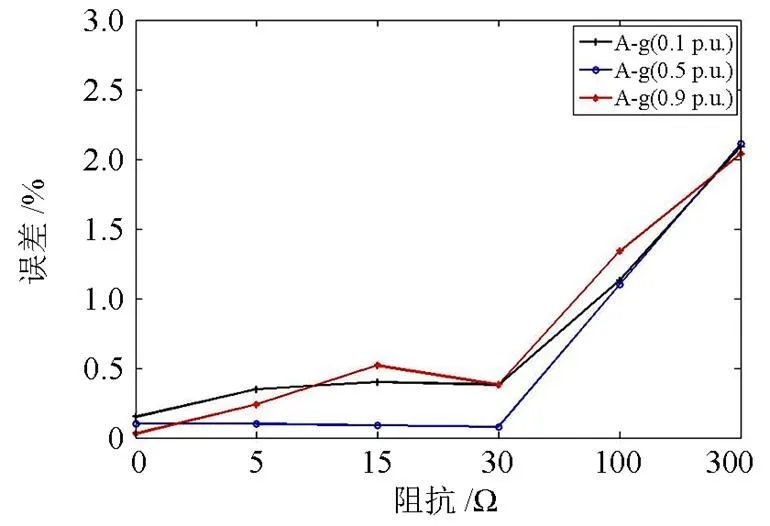
图8 线路23上单相接地故障(A-g)带不同故障通道电阻时的定位误差评估

5 结论

本文提出了一种基于故障可观性的输电线路故障定位方法，它提供了电网在信息不全条件下的故障定位方法。该方法采用分布参数输电线路模型，可以更准确地考虑分布电容电流对故障定位精度的影响；算法性能优异，且不受故障初始相位角、负荷及故障路径阻抗的影响；仅需要相量测量单元(PMU)的暂态数据信号，无需系统阻抗等其他信息；算法没有迭代过程，计算速度快。本方法可以应对各种线路故障，且便于电力系统实际应用。诸多仿真分析验证了该方法的有效性和鲁棒性。

[1] TAKAGI T T, YAMAKOSHI Y, BABA J, et al. Development of a new fault locator using the one-terminal voltage and current data[J]. IEEE Transactions on Power Apparatus and Systems, 1982, PAS-101(8): 2892-2898.

[2] XU Z, JIAO S, RAN L, et al. An online fault-locating scheme for EHV/UHV transmission lines[J]. IET Generation, Transmission & Distribution, 2008, 2(6): 789-799.

[3] GIRGIS A A, HART D G, PETERSON W L. A new fault location technique for two- and three-terminal lines[J]. IEEE Transactions on Power Delivery, 1992, 7(1): 98-107.

[4] 徐子华, 王艳松. 基于强跟踪滤波器的输电线路单端故障测距新方法[J]. 电力系统保护与控制, 2013, 41(7): 54-59.

XU Zihua, WANG Yansong. A new one-terminal fault location for transmission lines based on strong tracking filter[J]. Power System Protection and Control, 2013, 41(7): 54-59.

[5] 曲广龙, 杨洪耕, 吴晓清, 等. 考虑电网拓扑结构的行波故障定位方法[J]. 电力系统及其自动化学报, 2013, 25(6): 117-122.

QU Guanglong, YANG Honggeng, WU Xiaoqing, et al. Fault location with traveling wave considering network topological structure[J]. Proceedings of the CSU-EPSA, 2013, 25(6): 117-122.

[6] 钱佳琪, 叶佳卓, 旷哲, 等. 基于S变换的多端输电网故障定位方法[J]. 电力系统保护与控制, 2014, 42(23): 82-88.

QIAN Jiaqi, YE Jiazhuo, KUANG Zhe, et al. A fault- location method for multi-terminal transmission network based on S transform[J]. Power System Protection and Control, 2014, 42(23): 82-88.

[7] 赵军, 袁雪琼, 阮琦, 等. 基于对地参数跟踪测量的不接地系统单相接地故障选相研究[J]. 电力系统保护与控制, 2015, 43(21): 81-85.

ZHAO Jun, YUAN Xueqiong, RUAN Qi, et al. Research on single phase grounding fault phase selection based on ground parameter tracking and measurement[J]. Power System Protection and Control, 2015, 43(21): 81-85.

[8] 任琴, 舒勤, 刘勇. 基于对称注入法反射波特征提取的配电网故障测距算法[J]. 电力系统保护与控制, 2015, 43(24): 19-25.

REN Qin, SHU Qin, LIU Yong. A fault location algorithm for distribution network based on extracting features from the reflected wave of symmetrical injection method[J]. Power System Protection and Control, 2015, 43(24): 19-25.

[9] JIANG J A, YANG J Z, LIN Y H, et al. An adaptive PMU based fault detection/location technique for transmission lines, I: theory and algorithms[J]. IEEE Transactions on Power Delivery, 2000, 15(2): 486-493.

[10] JIANG J A, LIN Y H, YANG J Z, et al. An adaptive PMU based fault detection/location technique for transmission lines, II: PMU implementation and performance evaluation[J]. IEEE Transactions on Power Delivery, 2000, 15(4): 1136-1146.

[11] 鞠平. 电力系统广域测量技术[M]. 北京: 机械工业出版社, 2008.

[12] 王波, 周昱勇. 基于PMU的多端传输线路故障定位新方法[J]. 电力系统保护与控制, 2009, 37(12): 32-35, 39.

WANG Bo, ZHOU Yuyong. A novel PMU-based fault location algorithm for multi-terminal transmission line[J]. Power System Protection and Control, 2009, 37(12): 32-35, 39.

[13] LIEN K, LIU C, YU C, et al. Transmission network fault location observability with minimal PMU placement[J]. IEEE Transactions on Power Delivery, 2006, 21(3): 1128-1136.

[14] BALDWIN T L, MILI L, JR BOISEN M B, et al. Power system observability with minimal phasor measurement placement[J]. IEEE Transactions on Power Systems, 1993, 8(2): 707-715.

[15] 马杰, 李磊, 李乃永, 等. 基于故障信息的高阻接地故障辨识与定位方法[J]. 电力系统保护与控制, 2013, 41(11): 74-78.

MA Jie, LI Lei, LI Naiyong, et al. Identification and location of high-resistance grounding fault based on fault records[J]. Power System Protection and Control, 2013, 41(11): 74-78.

[16] 张怿宁, 束洪春, 田鑫萃, 等. 特高压直流输电线路接地极线路高阻故障测距方法研究[J]. 电力系统保护与控制, 2015, 43(24): 1-7.

ZHANG Yining, SHU Hongchun, TIAN Xincui, et al. Research on fault location algorithm for HVDC electrode line high impedance fault[J]. Power System Protection and Control, 2015, 43(24): 1-7.

[17] IEEE Standard C37.118-2005 (Revision of IEEE Std 1344-1995). IEEE standard for synchrophasors for power systems[S].

[18] 徐浩, 苗世洪, 姜臻, 等. 基于有限相量测量单元测量障分量信息的故障定位算法[J]. 电力系统自动化, 2013, 37(2): 43-48.

XU Hao, MIAO Shihong, JIANG Zhen, et al. A new fault location algorithm based on fault component from finite synchronized phasor measurement unit[J]. Automation of Electric Power Systems, 2013, 37(2): 43-48.

[19] 何仰赞, 温增银. 电力系统分析(上册) [M]. 武汉: 华中科技大学出版社, 2002.

[20] WANG Y J, LIU C W, LIU Y H. A PMU based special protection scheme: a case study of Taiwan power system[J]. Electrical Power and Energy Systems, 2005, 27: 215-223.

(编辑 葛艳娜)

Fault observability model based fault location technique for transmission grids

JIANG Zhen1, MIAO Shihong2, LIU Pei2

(1. Zhuhai Power Supply Bureau, Guangdong Power Grid Limited Liability Corporation, Zhuhai 519000, China; 2. State Key Laboratory of Advanced Electromagnetic Engineering and Technology (Huazhong University of Science and Technology), Wuhan 430074, China)

Extensive studies on WAMS based fault location technique are based on the idealized conditions of the measurement, so that they are limited in the actual applications in electric power system. In order to make the power grid to be provided reliable fault location technique on incomplete information conditions such as extreme weather, communication failures, etc., an effective fault location technique for transmission grids based on fault observability model is presented. High accuracy in fault location is achieved by using an accurate distributed parameter line model for the transmission lines. The performed work is provided with high performance which is featuring robustness to the uncertainties in fault inception angle, load current and fault path resistance. The transient fault data is obtained from PMUs in the proposed technique, and it does not require any information of the source impedance. This novel fault location technique does not need to be solved in an iterative manner and the calculation is fast. The validity and robustness of the proposed algorithm is evaluated by many simulations. This work is supported by National Natural Science Foundation of China (No. 51377068).

fault location; fault observability model; distributed parameters; incomplete information conditions; fault path resistance

10.7667/PSPC151528

国家自然科学基金项目(51377068)

2015-08-29；

2015-11-02

姜 臻(1986-)，男，博士，研究方向为电力系统安全分析、故障分析、继电保护及变电站自动化；E-mail: Jz8612@126.com 苗世洪(1963-)，男，教授，博士生导师，主要研究方向为电力系统安全控制、继电保护与自动化；E-mail: sa2000999@126.com 刘 沛(1944-)，女，教授，博士生导师，主要研究方向为电力系统继电保护及变电站综合自动化。E-mail: sunliupei@qq.com