精确制导武器打击下隧道建设安全距离研究
2016-04-11邱伟伟
钱 杰, 许 超, 邱伟伟
(1.军事交通学院学员旅6队,天津 300161;2.驻武汉铁路局襄阳军事代表办事处,湖北 襄阳 441000)
精确制导武器打击下隧道建设安全距离研究
钱 杰1, 许 超2, 邱伟伟2
(1.军事交通学院学员旅6队,天津 300161;2.驻武汉铁路局襄阳军事代表办事处,湖北 襄阳 441000)
摘要:在分析现行规章计算安全距离的方法存在不足的基础上,运用爆炸毁伤理论探究了精确制导武器打击下的毁伤机理,并选取2 000磅级GPS制导炸弹GBU-31和20 000磅级的GBU-43/B作为典型武器,计算得到隧道与桥梁、临近隧道等交通重点目标之间的安全距离。其计算方法和结果可以为隧道分级贯彻国防要求及制定相关技术标准提供参考。
关键词:隧道;安全距离;精确制导武器;贯彻国防要求
安全距离即安全防护距离,是指在打击某一重点目标时,在一次投弹的情况下,为防止误伤相邻重点目标或造成两个及以上重点目标同时遭到破坏,相邻重点目标之间应保持的最小距离。从近几次高技术局部战争来看,对于交通类重点目标,应以防常规武器破坏为主、防核武器破坏为辅,而对隧道等点(线)状交通重点目标而言,则应将精确制导武器打击作为防护重心。
1 对现行规章确定安全距离存在的不足分析
现行《××技术规程》确定隧道与其它重点目标之间的安全距离时,选取舰射巡航导弹BGM-109CⅢ及空射巡航导弹AGM-86C作为典型武器,并取毁伤半径R=14 m,存在两方面不足。
1.1 典型武器的选取难以满足需求
安全距离的确定应适应武器装备发展的需要。从美军在近几场高技术局部战争中所使用的精确制导武器的种类、数量、爆炸威力及取得的作战效果来分析,1 000磅级(1磅=0.454 kg)及以下的精确制导炸弹及巡航导弹等仍然是目前使用最多的制导武器,但2 000磅级以上制导武器在总投弹中的比例逐步上升,并取得了很好的作战效果。目前,爆破型制导武器中威力最大的是拥有“炸弹之母”称号的GBU-43/B(MOAB),其圆径达到20 000磅级。由此可见,仅考虑1 000磅级制导炸弹袭击时的安全距离已经难以适应现代高技术局部战争条件下的防护需求。
1.2 毁伤半径的确定不够科学
武器的毁伤半径是个相对的概念,对不同类型的交通重点目标而言,由于毁伤机理及结构自身的抗毁能力不同,同一类型武器对不同类型交通重点目标的破坏范围是不同的。而现行规程没有针对不同类型的交通基础设施加以区分,缺乏合理性。
本文基于以上两点不足,利用爆炸毁伤相关理论,对隧道建设时应满足的安全距离重新进行计算。
2 利用爆炸毁伤理论确定武器毁伤半径
2.1基本理论公式
隧道建设应满足的安全距离需求主要取决于弹着点的偏差、武器的毁伤能力以及一次投弹数量。弹着点偏差越大、武器的毁伤能力越强、一次投弹数量越多,则安全距离要求就越大。其中,弹着点的偏差不仅与武器的命中精度有关,还与飞行员的战斗技能密不可分,而武器的毁伤能力则主要取决于战斗部装药性质与装药量。参考相关资料,安全距离可按下式计算[1]:
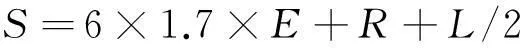
(1)
式中:S为安全距离(m);E为概率偏差(m),与圆概率偏差ε的换算公式为E=0.572 86ε;R为战斗部对防护目标的毁伤半径(m);L为投掷多枚弹药时的连投长度(m)。
对于精确制导武器,一般不考虑连投的情况,安全距离可按下式计算:
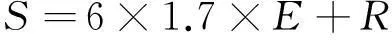
(2)
当武器命中精度极高,导致弹着点偏差小于武器的毁伤半径时,为确保两个重点目标不被同时炸毁,安全距离宜不小于武器对两个相邻重点目标各自毁伤半径之和,即:
(3)
2.2 爆炸毁伤基本理论
当空袭弹药爆炸时,对目标的毁伤是由空气冲击波、地震波、爆炸产物等诸多因素的综合作用所引起的。一般而言,当炸药在空气中爆炸时,形成空气冲击波的能量约占爆炸总能量的70%,且空气冲击波造成的破坏范围也大于其它因素的破坏范围[2]。故对隧道等建筑类目标而言,确定毁伤半径时应主要考虑空气冲击波的破坏作用。
空气冲击波对建筑类目标产生破坏作用不仅与超压有关,还与作用时间有关。相应地,可以用超压(ΔP)准则和超压—比冲量(ΔP-i)准则来衡量冲击波的破坏能力。空袭武器一般都是采用高能量密度的炸药,对于这类爆源,采用超压准则就隐含地引入了比冲量[3],故应该以超压准则来分析其破坏作用,其唯一参数是冲击波峰值超压。冲击波峰值超压对建筑类目标的破坏影响如表1所示。

表1 峰值超压对建筑物目标的破坏影响
2.3 冲击波峰值超压的计算
在无弹壳情况下,球形装药(装药形状对空气冲击波的影响只在离爆炸中心较近时比较大,当距离较远时影响很小,空袭武器可以按照球形装药的方法进行计算)炸药在无限空气介质中爆炸时的峰值超压可以按照以下经验公式进行计算[2]:
(4)
式中:ΔPm为在空气中爆炸时的空气冲击波峰值超压(105Pa);r为距爆心的距离(m);ω为TNT当量(kg)。
当空袭武器用于打击隧道时,一般是在地面爆炸,由于地面的阻挡,空气冲击波不是向整个空间传播,而只向一半无限空间传播,被冲击波带动的空气量也减少一半。炸药在刚性地面爆炸时,相当于两倍的装药在无限空间爆炸,可用ω′=2ω代替ω进行计算,而对于普通土壤,可取ω′=1.7~1.8ω进行计算[2]。山区土质达不到刚性地面的强度,为安全起见,本文选取ω′=1.8ω进行计算,代入公式(4)可得在地面爆炸时的空气冲击波峰值超压:
(5)
公式(5)是在无弹壳的情况下计算得到空气冲击波峰值超压值,实际上,空袭弹药都是带弹壳的,爆炸产生的能量不可能完全用来形成空气冲击波,而是有一部分通过转化为其它形式的能量得以释放,形成空气冲击波的炸药当量按下式计算[2]:
(6)
式中:α为战斗部装填系数;r0为装药半径;rm为破片达到最大速度时的半径,钢壳弹体rm≈1.5 r0。
求出ωbe后,替代公式(5)中的ω值进行计算,即可得到离爆心r处的峰值超压值。
3 确定隧道建设安全距离赋值与计算
3.1典型武器的选取
美国是世界上头号军事强国,也是近几十年发动战争最频繁的国家。从美军现役常用制导弹药的种类和型号来分析,采用爆破型战斗部的制导武器圆径主要有250磅、500磅、1 000磅和2 000磅等。其中,GBU-43/B(MOAB)是为数不多的2 000磅级以上制导武器类型之一,也是美军研制用来专门对付洞穴及隧道的新式武器。本文选取美军在伊拉克战争中使用最多的2 000磅级GPS制导炸弹GBU-31和爆炸威力最大的GBU-43/B作为典型武器,其主要技术性能参数见表2。

表2 GBU-31和GBU-43/B部分技术性能参数
3.2 毁伤半径计算
结合表2,取rm=1.5 r0,α=0.48,ω=514.8 kg,代入公式(6)可得GBU-31爆炸时形成冲击波的炸药当量为232.1 kg;取rm=1.5 r0,α=0.9, ω=9 328 kg,代入公式(6)可得GBU-43/B爆炸时形成冲击波的炸药当量为7 967 kg。
由公式(5)可知,当爆炸时形成冲击波的炸药当量确定后,冲击波峰值超压是距爆心距离r的一元函数,结合表1及公式(5),可以计算得出GBU-31与GBU-43/B破坏不同目标时的毁伤半径,如表3所示。

表3 GBU-31与GBU-43/B破坏不同目标时的毁伤半径 m
3.3 安全距离计算
隧道与军事重点目标以及机场、铁路站场等面状交通重点目标的安全距离宜考虑普通弹药连投的情况,安全距离宜不小于x m。这一安全距离值大于考虑制导武器打击时的安全距离值,因而不需要再重复计算制导武器打击时的安全距离。故只计算隧道与点、线状重点目标的安全距离,主要是隧道与桥梁和临近隧道之间的安全距离。
3.3.1 隧道与桥梁之间
确定重点隧道与重点桥梁之间的安全距离应同时考虑打击隧道时不误伤桥梁和打击桥梁时不误伤隧道两种情况,毁伤半径宜从武器打击时对桥梁和隧道各自的破坏范围中取最大值。
(1)视钢筋混凝土桥和隧道同为防地震钢筋混凝土建筑物,由表3可知GBU-31和GBU-43/B对这类建筑物的毁伤半径分别为14.8~16.9 m和48.2~55 m,根据公式(2)计算得到钢筋混凝土桥和隧道之间的安全距离分别为73.2~75.3 m和106.6~113.4 m。
(2)计算重点隧道与钢架桥的安全距离时,若按照打击隧道时不误伤钢架桥计算,由表3可知GBU-31和GBU-43/B对钢架桥的毁伤半径分别为12.4~14.8 m和40.4~48.2 m,同理计算得到安全距离分别为70.8~73.2 m和98.8~106.6 m;若按打击钢架桥时不误伤隧道计算,GBU-31和GBU-43/B对隧道的毁伤半径分别为14.8~16.9 m和48.2~55 m,则安全距离分别为73.2~75.3 m和106.6~113.4 m。综上,安全距离宜取两种情况下的较大值。
3.3.2 隧道与隧道之间
(1)对于并行设置的公路隧道与铁路隧道之间和上下行分离式铁路隧道双洞之间的安全距离,根据之前的计算结果,防GBU-31和GBU-43/B袭击时的安全距离分别为73.2~75.3 m和106.6~113.4 m。
(2)对于分离式独立双洞公路隧道,由于双洞之间需要修建车行横通道,考虑到横通道的建设费用,双洞线间距不宜过大,但应满足双洞不被同时炸毁的要求,双洞线间距宜不小于毁伤直径,仅考虑防2 000磅级制导弹药的需求时,其安全距离为29.6~33.8 m。
4 结束语
保持重点隧道与其它交通重点目标之间的安全距离,是隧道建设贯彻国防要求的一项重要内容。通过计算在防2 000磅级和20 000磅级制导炸弹打击下,隧道与不同交通重点目标之间应保持的安全距离,为隧道建设过程中分级贯彻国防要求提供参考依据,对提高隧道和其它交通重点目标在武器打击时的生存能力具有积极意义。
参考文献
[1]徐理博,许 超.2 000磅级制导弹药打击下桥梁建设的安全距离研究[J].国防交通工程与技术,2013(5):34-37
[2]北京工业学院八系编写组.爆炸及其作用:下册[M].北京:国防工业出版社,1979
[3]董守华,李晓杰.事故爆炸冲击波破坏准则综述[J].石油化工安全技术,1996(4):40-41
A Study of the Safe Distance for the Construction of Tunnels Probably to be Attacked by Precision-Guided Weapons
Qian Jie1,Xu Chao2,Qiu Weiwei2
( 1.Team 6 of the Students Brigade of the Military Traffic Institute of the PLA of China,Tianjin 300161,China;2.Office of the Military Representative Stationed to Xiangyang of the Wuhan Railway Bureau,Xiangyang 441000,China )
Abstract:Upon the basis of analyzing the shortcomings of the existing methods of the norms in calculating the safe distance,the destroying and damaging mechanism of the precision-guided weapon is explored in the paper by means of the blasting-caused-destroying-and-damaging theory.With bombs of the 2000-pound-grade GPS-guided GBU-31 and the 20000-pound-grade GBU-43-B chosen as the typical weapons,the safe distances between a tunnel and a bridge, a tunnel and another neighboring tunnel, and a tunnel and other important traffic routes or other traffic facilities,are obtained through calculations.Both the calculated results and the calculating methods may serve as a useful reference for drafting corresponding standards and grading tunnels in carrying out the requirements in national defense.
Key words:tunnel;safe distance;precision-guided weapon;carry out the requirements in national defense
中图分类号:U458
文献标识码:A
文章编号:1672-3953(2016)02-0037-04
DOI:10.13219/j.gjgyat.2016.02.010
作者简介:钱杰(1995—),男,学生421186703@qq.com
收稿日期:2016-01-28
