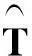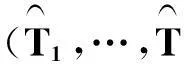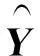中国宏观经济数据的结构断点分析与单位根检验
2016-04-11付连艳孟庆元
付连艳,曲 爽,孟庆元
(1.辽宁大学经济学院,辽宁 沈阳 110036;
2.长春师范大学数学学院,吉林 长春 130032;
3.吉林交通职业技术学院,吉林 长春 130012)
中国宏观经济数据的结构断点分析与单位根检验
付连艳1,曲爽2,孟庆元3
(1.辽宁大学经济学院,辽宁 沈阳 110036;
2.长春师范大学数学学院,吉林 长春 130032;
3.吉林交通职业技术学院,吉林 长春 130012)
[摘要]以对数GDP数据为依据,通过AIC方法确定结构断点个数,从而估计出中国经济发展经历了三个发展阶段:1952—1979;1980—1993;1994—2010. 运用ADF和PP两种单位根检验方法验证了对数GDP数据运行趋势的平稳性. 避免了因遗漏时间趋势中的断点所导致最小二乘估计有偏差且不一致的情况.
[关键词]确定性时间趋势;结构断点;趋势平稳;长期增长;单位根检验
1预备知识
许多经济和金融的时间序列数据都呈现出具有趋势性或非平稳性均值的特征,如资产价格、汇率、GDP的宏观经济总量数据等.计量经济学一个很重要的任务就是给出这些数据恰当的趋势分析.[1]如果去掉趋势后的序列是平稳过程,我们就称该序列有确定性趋势,模型可写作Yt=μt+ut,其中E(ut)=0.若μt=α+βt,则该序列在整个时间区间内趋势相同. 在实际应用中,经济政策的改变、重大事件的发生、经济体制的改革等都有可能促使趋势函数随时间的推移而发生改变,这样的事件、改变、改革被称为结构变化或结构断点.如果趋势函数随时间发生了改变,而在分析过程中却忽略了这一变化,就会得到错误的推断和预测,其后果会造成最小二乘估计有偏且不一致,更严重的后果是不能拒绝单位根假设.
自从Dickey和Fuller开创性地提出使用DF统计量进行单位根检验以来,计量经济领域就一直关注单位根检验问题.[2]DF检验是基于AR(1)模型(一阶自回归模型),而后被推广到更高阶的AR(n)模型,即ADF检验(扩展的DF检验).拒绝单位根检验意味着序列平稳,否则序列不平稳.平稳序列满足均值、方差均为常数,协方差与时间无关的性质;非平稳序列的方差经常随着时间的推移而增加,这时其预测完全不可信.因此,对一个时间序列预测其未来走势之前,应先检验其平稳性,这使得单位根检验在实际中意义重大.Nelson和Plosser[3]利用ADF方法对美国宏观经济数据的平稳性进行分析,这一工作使DF与ADF方法广为流行.他们的研究结果表明美国宏观经济数据不能拒绝单位根假设,即序列不是趋势平稳的,从而认为美国经济没有稳定的长期增长趋势.但是,由于该文作者没有考虑结构断点,使得这个结果存在争议.Perron允许在原假设和被择假设的趋势函数中存在一个断点,他证明了忽视趋势函数中的断点将误导拒绝单位根假设的结论.[4]Perron称如果允许一个断点存在的话,许多的宏观经济时间序列都能表示成围绕确定性趋势函数平稳波动的形式.关于结构断点的问题,代表性的工作参见文献[5-14].
前人研究结果表明,忽略结构断点很可能造成检验结果的误判.在单位根检验中加入几个断点也会直接影响检验的结果.本文关注中国经济增长情况,以对数GDP数据为依据,探究中国经济增长经历了几个发展阶段.应用Akaike信息判决准则(AIC)[15]确定结构断点个数,进而估计经济增长发展阶段的个数.最后使用ADF与PP方法进行单位根检验,完善了含有断点的单位根检测理论.最终得出的中国经济发展结构断点(1979年和1993年)与历史事件相符合.
2统计建模
时间序列可以表示成确定性时间函数与均值为0的随机过程之和的形式.用Yt表示时间序列,μt是趋势项,ut是残差序列.考虑如下模型:
Yt=μt+ut,
(1)
其中去势后的序列ut是平稳序列,且E(ut)=0.特别地,假设ut是白噪声序列,如果去势后的过程平稳,那么存在确定性趋势;否则称存在的是随机趋势.假设确定性趋势是时间的线性函数,即
μt=α+βt.
模型(1)中,μt是对任意时间t定义的.因此,若
μt=α+βt,
则在整个时间区间内有共同的线性时间趋势.
当经济结构等发生变化时,时间趋势也会随之改变.假设在趋势项中存在M个阶段,即M个不同的时间趋势(这里M未知),即假设
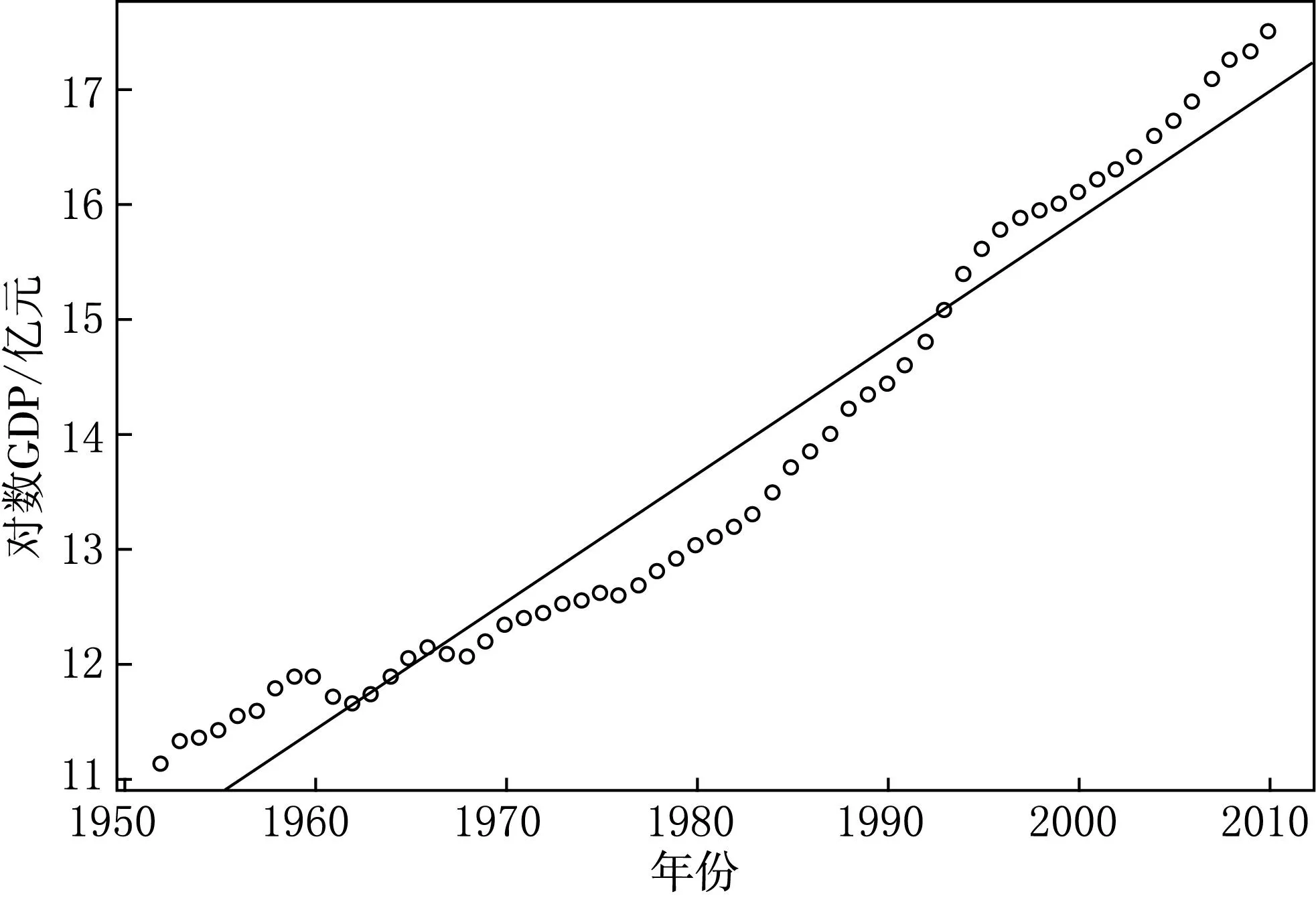
其中Tm(m=1,…,M-1)被称作结构断点.为简化模型形式,我们引入哑变量Dm=I(Tm (2) 在回归函数中忽略哑变量(也即丢掉断点)会导致最小二乘估计有偏且不一致,甚至会导致一个更严重的后果:不能够拒绝单位根假设.这意味着该序列是非平稳的,没有长期增长趋势.[16] 3估计与检验 3.1选择阶段个数M 本文中趋势项分段个数M不需人为事先确定.这里借助AIC方法,先拟合所有的结构变化模型,然后选择使得AIC取值最小的M. 其中2M为含有M阶段趋势模型中的参数个数.AIC定义式中的第二项被称为判决惩罚函数,它用模型中的参数个数对模型进行惩罚.这里应用数据挖掘的思想,将所有数据全部运算一遍后选出最合理的阶段数M. 3.2估计断点位置 (3) (4) 其中 3.3自回归单位根检验 检验的原假设是存在单位根,被择假设是趋势平稳. 我们对去掉趋势项μt后的序列ut进行AR(1)单位根假设,模型如下: ut=ρut-1+εt, (5) 我们在该部分应用ADF与PP方法进行单位根检验.模型(5)可以扩展到AR(p)模型,方法与AR(1)类似.原假设ρ0=1对应被择假设ρ0<1.在原假设下,ut是随机游走过程,该过程非平稳.在被择假设ρ0<1下,去势后序列ut是平稳的AR(1)过程. 4实证分析 我们利用对数GDP数据研究了中国经济发展的整体状况,主要包括中国经济发展的平衡性与阶段性,使用的数据包括1952—2010年的59个GDP年观测数据,数据来源于《中国统计年鉴》和《新中国50年汇编》. 当假设整个区间有相同的线性时间趋势时,我们给出基于最小二乘方法的时间趋势线,见图1.不难发现图1拟合效果不是很好,并且实证结果没能够拒绝单位根原假设(p-值=0.328 6).因此,用该趋势衡量我国经济长期增长是不准确的. 得到如下回归方程: (6) 这个结果是由于忽略了结构断点导致的.由图1可见,在1952—2010年间,中国经济的增长趋势发生了明显的变化.那么,中国经济发展分为几个阶段合适呢?我们最终发现3个阶段是恰当的.实证分析结果表明AIC在M=3时达到了最小值,两个结构断点分别是1979年和1993年.结果见表1. 图1 1952—2010年对数GDP数据的散点图和回归直线 M1234AIC-1.66-4.17-4.31-4.28 在回归模型中加入两个哑变量D1=I(1979 (7) 显然,带断点的回归结果拟合得要好得多.对去势后序列进一步做单位根检验,结果显示很容易拒绝单位根假设(p-值=0.009).图2显示了由该回归结果得到的长期增长路径. 图2 1952—2010年对数GDP数据分为3个阶段的时间趋势图 增长率是趋势线的斜率值.由该图形可以获知在每个不同的增长期都有各自的长期增长率.根据实证结果,我们总结出下列结构断点的日期,并发现我国几个关键性的经济和金融时间点,与序列中的结构断点相对应: (1) 第一个结构断点发生在1979年,主要是由市场经济改革造成的. 自从市场经济体制改革从1979年实施以来,中国经济结构和机制发生了显著变化. (2) 第二个断点发生在1993年,是紧随邓小平同志1992年南行讲话之后的一年,改革空间加大,相应投资和增长速度增加. 5结论 本文研究中国GDP的对数数据,根据实证结果,我们得到以下结论:中国GDP的增长趋势存在两个结构断点,并且都与关键的经济和金融时间点相对应;中国经济增长已经经历了3个发展阶段:1952—1979;1980—1993;1994—2010. [参考文献] [1]ZIVOT E,WANG J H.Modeling financial time series with S-PLUS[M].New York:Springer-Verlag,2002:107. [2]DICKEY D,FULLER W.Distribution of the estimators for autoregressive time series with a unit root[J]. Journal of American Statistical Association,1979,74:427-431. [3]NELSON C R,PLOSSER C I.Trends and random walks in macroeconomic time series[J]. Journal of Monetary Economics,1982,10:139-162. [4]PERRON P.The great crash,the oil price shock and the unit root hypothesis[J]. Econometrica,1989,57:1361-1401. [5]ANDREWS D W K.Tests for parameter instability and structural change with unknown change point[J]. Econometrica,1993,61:821-856. [6]BAI J,PERRON P.Estimating and testing linear models with multiple structural changes[J]. Econometrica,1998,66:47-78. [7]BAI J,PERRON P.Computation and analysis of multiple structural change models[J]. Journal of Applied Econometrics,2003a,18:1-22. [8]BAI J.Likelihood ratio tests for multiple structural changes[J]. Journal of Econometrics,1999,91:299-323. [9]HANSEN B E.Testing for structural change in conditional models[J]. Journal of Econometrics,2000,97:93-115. [10]KUAN C M,HSU C C.Change point estimation of fractionally integrated processes[J]. Journal of Time Series Analysis,1998,19:693-708. [11]BANERJEE A,URGA G.Modelling structural breaks,long memory and stock market volatility:an overview[J]. Journal of Econometrics,2005,129:1-34. [12]PERRON P,VOGELSANG T J.Testing for a unit root in a time series with a shift in mean,corrections and extensions[J]. Journal of Business and Economic Statistics,1992,10:467-470. [13]PERRON P.Further evidence from breaking trend functions in macroeconomic variables[J]. Journal of Econometrics,1997,80:355-385. [14]VOGELSANG T J,PERRON P.Additional tests for unit root allowing the possibility of breaks in the trend function [J]. International Economic Review,1998,39:1073-1110. [15]AKAIKE H.Information theory and the extension of the maximum likelihood principle[C]//Petrow B N,Csaki F,International Symposium of Information Theory,Budapest:Akademia Kiado,1973:267-281. [16]吕建雄,李鑫,程道文.线性回归方法在核数据处理中的应用[J].东北师大学报(自然科学版),2014,46(4):72-76. (责任编辑:李亚军) Analysis of structural breaks and unit root tests for Chinese macroeconomic data FU Lian-yan1,QU Shuang2,MENG Qing-yuan3 (1.Faculty of Economics,Liaoning University,Shenyang 110036,China;2.Faculty of Mathematics,Changchun Normal University,Changchun 130024,China;3.Jilin Communications Polytechnic,Changchun 130012,China) Abstract:This paper focuses on China growth behavior. AIC method is applied to obtain that China growth has gone thorough 3 stages:1952—1979;1980—1993;1994—2010. Then we verify the series are trend stationary by rejecting unit root null hypothesis using ADF and PP methods.All the results overcome the shortcomings of OLS estimator to be biased and inconsistent,which is caused by the omission of breaks in the time trend. Keywords:determined time trend;structural breaks;trend stationary;long-run growth;unit root test [中图分类号]O 212[学科代码]110·67 [文献标志码]A [作者简介]付连艳(1980—),女,博士,副教授,主要从事处理效应评估和序约束的统计方法研究; 通讯作者:曲爽(1981—),女,硕士,讲师,主要从事贝叶斯统计和教育统计研究. [基金项目]国家自然科学基金资助项目(11301245). [收稿日期]2014-04-28 [文章编号]1000-1832(2016)01-0029-05 [DOI]10.16163/j.cnki.22-1123/n.2016.01.008