函数组的广义仿射线性相关性及其推广
2016-04-11孙爱慧程晓亮吴秀兰
孙爱慧,程晓亮,吴秀兰
(吉林师范大学数学学院,吉林 四平 136000)
函数组的广义仿射线性相关性及其推广
孙爱慧,程晓亮,吴秀兰
(吉林师范大学数学学院,吉林 四平 136000)
[摘要]给出了函数组广义仿射线性相关与强仿射线性相关等概念,得到了函数组及其导函数组广义仿射线性相关的充要条件和必要条件,证明了函数组线性相关与仿射线性相关等价的条件.
[关键词]函数组;线性相关;强线性相关;广义仿射线性相关;强广义仿射线性相关
在代数学的发展进程中,线性相关性一直是人们热衷的问题之一:文献[1-2]给出了向量组线性相关性的概念和一些重要结论;文献[3]提出了向量组强线性相关性的概念与一些相关结论;文献[4-5]将仿射线性相关性和强仿射线性相关性的概念引入到向量组中;文献[6-7]将线性相关性和广义线性相关性引入到数列组中.受此启发,将向量组的情形一般化到函数组、将仿射线性相关等性质引入到函数组并推广到广义的情形是十分必要的.
1预备知识
用f(x),g(x),h(x)表示定义在区间I上的一元实函数,为了书写简便,简记为f,g,h.我们约定:同一个定义或定理中出现的函数的定义域均相同;文中出现的数均为实数.
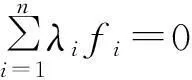
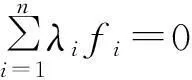


2主要结果
定理1已知F1,F2,…,Fn是定义在区间I上的n个C1-函数,f1,f2,…,fn是其导函数组.则F1,F2,…,Fn广义仿射线性相关,当且仅当f1,f2,…,fn仿射线性相关.
证明先证必要性.由已知,存在不全为零的n个实数λ1,λ2,…,λn,使得∀x∈I,
λ1F1+λ2F2+…+λnFn+a=0.
对该式两端求导得

即
λ1f1+λ2f2+…+λnfn=0,
从而f1,f2,…,fn仿射线性相关.
下证充分性.由f1,f2,…,fn仿射线性相关,一定存在不全为零的n个数λ1,λ2,…,λn,使得
λ1f1+λ2f2+…+λnfn=0.
又知F1,F2,…,Fn分别是f1,f2,…,fn的原函数,故对等式λ1f1+λ2f2+…+λnfn=0两端同时求不定积分有
∫λ1f1dx+∫λ2f2dx+…+∫λnfndx=0,
即
λ1F1+C1+λ2F2+C2+…+λnFn+Cn=0.
令C1+C2+…+Cn=a,则
λ1F1+λ2F2+…+λnFn+a=0,
即F1,F2,…,Fn广义仿射线性相关.
推论1设F1,F2,…,Fn是定义在区间I上的n个C1-函数,f1,f2,…,fn是其导函数组.则F1,F2,…,Fn强广义仿射线性相关,当且仅当f1,f2,…,fn强仿射线性相关.
推论2设A:f1,f2,…,fn是定义在区间I上的n个Cm-函数.若函数组A广义仿射线性相关,则
必仿射线性相关.进一步地,若m≥n,则


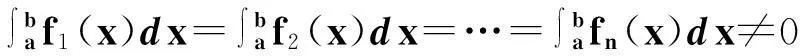
则A线性相关,当且仅当A仿射线性相关.


即

设

则
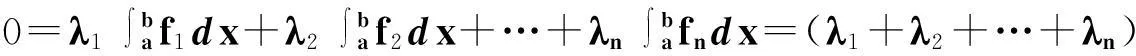
而d≠0,故λ1+λ2+…+λn=0.即函数组A仿射线性相关.
类似地,我们可以得到下面结论.

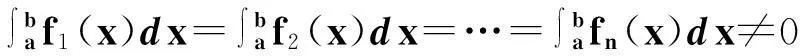
则A强线性相关,当且仅当A强仿射线性相关.
我们下一步试图将本文中函数组的结论推广到向量函数组上,同时由于文献[8]中给出了向量函数微分的非标准定义,于是,我们还要将着眼点放到更一般的非标准微分的情形上.
[参考文献]
[1]北京大学数学系.高等代数[M].北京:高等教育出版社,2013:164-167.
[2]张禾瑞,郝炳新.高等代数[M].北京:高等教育出版社,2007:217-254.
[3]杨闻起.强线性相关性与弱无关性[J].宝鸡文理学院学报,2009,29(2):1-3.
[4]香花.关于仿射线性相关性的探讨[J].数学实践与认识,2012,42(7):219-225.
[5]香花.强仿射线性相关性与强线性相关性[J].安徽师范大学学报,2013,36(3):211-215.
[6]杨建华.数列组的齐次线性相关性[J].武汉工程大学学报,2009,31(9):81-82.
[7]杨建华.数列组的广义线性相关性[J].武汉工程大学学报,2009,31(12):79-81.
[8]陈东立,史艳维,董欢欢.向量函数微分的非标准定义[J].东北师大学报(自然科学版),2015,47(3):37-39.
(责任编辑:李亚军)
The generalized affine linear correlation of function group and the forms of promotion
SUN Ai-hui,CHENG Xiao-liang,WU Xiu-lan
(College of Mathematics,Jilin Normal University,Siping 136000,China)
Abstract:The present paper puts forward the concepts on generalized and strongly generalized affine linear correlation of function group. Some sufficient and necessary conditions are deduced to judge the generalized or strongly generalized affine correlation between the function group and its derivatives,as well as a necessary and sufficient condition on linear correlation and affine linear correlation of function group.
Keywords:function group;linear correlation;strongly linear correlation;generalized affine linear correlation;strongly generalized affine linear correlation
[中图分类号]O 151[学科代码]110·21
[文献标志码]A
[作者简介]孙爱慧(1978—),女,硕士,主要从事基础数学研究.
[基金项目]国家自然科学基金资助项目(11301215);吉林省青年科研基金资助项目(20130522094H).
[收稿日期]2014-10-11
[文章编号]1000-1832(2016)01-0005-03
[DOI]10.16163/j.cnki.22-1123/n.2016.01.002
