轮轨垂向力识别的时域方法

孙善超，王卫东，刘金朝

( 1．中国铁道科学研究院，北京　100081; 2．中国铁道科学研究院基础设施检测研究所，北京　100081)



轮轨垂向力识别的时域方法

孙善超1，王卫东1，刘金朝2

( 1．中国铁道科学研究院，北京100081; 2．中国铁道科学研究院基础设施检测研究所，北京100081)

摘要:基于虚拟样机技术建立CRH2高速检测车的动力学仿真模型(正演模型)，并利用试验数据进行了模型验证。利用动力学仿真模型计算得到轮轨垂向力及轴箱垂向加速度。结合车辆—轨道系统的特点，将车轮看作一个单自由度振动系统，建立单自由度轮轨垂向力识别模型。基于杜哈密积分，在时域内推导了在线轮轨力识别算法。将正演模型的轴箱加速度作为输入，利用单自由度轮轨垂向力识别模型对轮轨垂向力进行了识别。识别结果与正演模型的轮轨力进行比较，两者相关系数达到0. 82。该识别模型基于轴箱加速度逐点运算，可以快速高效地对轮轨垂向作用力进行识别，并实时监测轮轨状态。基于车轮动力学理论，建立多自由度轮轨垂向力反演模型:首先建立了轮对的横向、沉浮、侧滚等轮对运动方程，然后对部分参数加以简化，最后基于车辆—轨道系统的运动特点，将轮对运动方程解耦成单自由度进行求解。利用该模型识别的轮轨垂向力与正演模型轮轨力的相关系数达到0. 97。单自由度车轮模型较为简单，但识别精度稍低;多自由度轮对模型较为复杂，但识别精度较高。两种模型的识别结果均满足工程需求，可以根据不同的需求选用不同的模型。

关键词:轮轨垂向力载荷识别时域模型杜哈密积分

1　概述

轮轨之间的作用力是衡量铁路运行安全性的重要参数。轮轨力测量最直接的方法是采用测力轮对，但测力轮对的价格较高，使用寿命较短，安装不像加速度传感器那样方便。因此国内外都只有少数车辆安装测力轮对，仅在情况比较复杂，需直接判断轨道不平顺的影响时才使用。为了达到降低检测成本、简化维护等目的，需要基于易于测量的车辆响应数据进行轮轨力的载荷识别研究。

载荷识别在结构动力学中属于第二类反问题。它是根据结构响应(如应变、加速度等)并结合结构系统的数学模型对系统的输入进行识别。传统的动态载荷识别方法主要有频域法与时域法2种。

频域法主要是根据测得的响应，依据系统的传递函数矩阵与响应谱的关系，在频域内确定动态载荷谱，或经模态坐标变换计算模态力在频域内的特性。该方法比较成熟。一般适用于稳态动态载荷或平稳随机载荷的识别［1-3］。

时域法是20世纪80年代中期发展起来的一种方法，其基本思想是利用结构的模型参数如质量、刚度、阻尼等建立系统在时域内的逆向模型，通过测量结构系统响应来识别输入的动态载荷。常用的方法有基于逆系统的动载荷识别技术、基于广义正交域级数展开的动载荷识别技术、基于加权加速度求和的动载荷识别技术( SWAT)、基于小波分析的动载荷识别技术等。

近年来，一些新型的算法被开发出来，应用于实际工程，并逐渐推广到动态载荷识别领域，如模拟人工智能的神经网络算法、模拟生物进化理论的遗传算法、模仿生物行为的蚁群算法等［4-6］。这些算法被广泛应用到桥梁等工程结构体的载荷识别及载荷作用点位置识别中，取得了较好的效果，但是由于列车运行速度较高，尚不能直接应用于轮轨力快速识别。为了保障列车运行安全，需要一种快速的在线高精度算法来实时监控列车的运行状态。

2000年以后陆续有人进行这方面的研究。2003年，LARS［7］提出了车辆轮轨力的识别方法，但是反演模型不是基于车体的加速度，不适用于车载、实时系统。2004年日本的FURUKAW［8-9］建立了车辆系统状态空间方程，利用轴箱加速度对垂向轮轨力进行识别。该方法仅仅利用轴箱加速度进行载荷识别，从机理上决定了其无法达到较高的识别精度。2004年波兰的UHL［10-11］提出了一种基于测得的系统响应，利用遗传算法进行载荷识别的方法。2007—2008年，XIA等［12-14］提出了一种基于车体加速度的铁道货车反演模型，并对一定速度下的轮轨力进行识别。其计算过程中需要输入轨道不平顺，限制了其在运营车辆上的应用。

本文基于车辆—轨道系统的特点，从保障铁路安全的角度出发，在时域推导了一种快速的实时在线载荷识别算法，并给出了单车轮轮轨力识别模型及更高精度的轮对轮轨力识别模型。所建模型以轴箱加速度作为输入，在时域内对轮轨力进行识别，效果较好。该方法仅仅把加速度作为识别输入，无需轨道不平顺、位移、速度等响应数据，因此便于推广应用。

2　正演模型的建立及验证

根据CRH2高速检测车转向架动力学参数，建立如图1所示的动力学正演模型。其中转向架由构架、前后2个轮对、4个轴箱、制动装置、牵引拉杆及弹性阻尼元件组成。根据CRH2高速检测车车体的参数建立车体动力学模型，把车体和转向架的动力学模型进行装配，得到CRH2高速检测车的动力学仿真模型，如图2所示。

图1 CRH2高速检测车转向架的动力学模型

图2 CRH2高速检测车动力学模型

图3为武广线某段直线线路预设的轨道不平顺波形。利用该处轨道不平顺及CRH2高速检测车测得的车体加速度响应进行CRH2高速检测车动力学模型的验证。

图3预设的轨道不平顺波形

根据上述线路的几何参数建立其轨道动力学模型。将建立的CRH2高速检测车的动力学模型置于轨道动力学模型上进行车辆动力学仿真，得到车体垂向加速度，并与对应线路上的测试值进行对比，如图4所示。

图4车体垂向加速度的仿真值与实测值对比

实测值与仿真值的相关系数的计算公式为

3单自由度轮轨垂向力反演模型

3. 1模型的建立

取列车一轴的左侧车轮进行分析，建立如图5( a)所示的车轮单自由度模型。对其进行简化，并简化为如图5( b)所示的单自由度振动系统。其振动方程为

在轮轨垂向力f ( t)的作用下，由杜哈密积分( Duhamel Integral)可得车轮的位移、速度和加速度［3］。

图5车轮单自由度模型及其概化

对式( 3)进行离散化，设ti－ti－1=Δt，并假设ti－1时刻为0时刻，则ti时刻的位移如下

在［ti－1，ti］时段，令τ=τ1+ ti－1，则

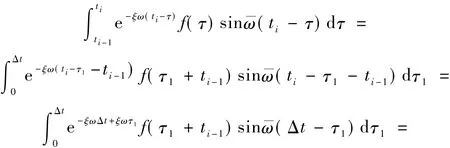
把式( 7)中的τ1用τ替代，并代入式( 6)，可得

同理可得到速度和加速度的表达式。将速度和位移代入加速度表达式中，得

在［ti－1，ti］时段，假设作用力f( t)为一常值，并令其值为fi－1，经分步积分，得到

把式( 11)—式( 13)分别代入式( 8)—式( 10)，得

将力表示成位移、速度、加速度的表达式，式( 16)可以写成

初始条件取车轮—轨道系统静平衡状态，由式( 17)计算出fi－1，代入式( 14)、式( 15)，计算出x( ti)( ti)，然后再代入式( 17)，结合已知的计算出fi。这样逐步计算，可反演出轮轨垂向力的变化曲线。

3. 2车轮单自由度模型轮轨垂向力识别

利用正演模型，输入轨道不平顺，可以计算出一轴左侧轴箱垂向加速度(图6)和轮轨垂向作用力(图7( a)中虚线)。利用3. 1中的识别模型，将轴箱加速度作为输入，对轮轨垂向力进行快速识别，识别结果如图7( a)中实线所示。局部放大图如7( b)所示。经计算两条曲线的相关系数达到0. 82，识别结果较为理想。

图6采用正演模型计算出的轴箱垂向加速度

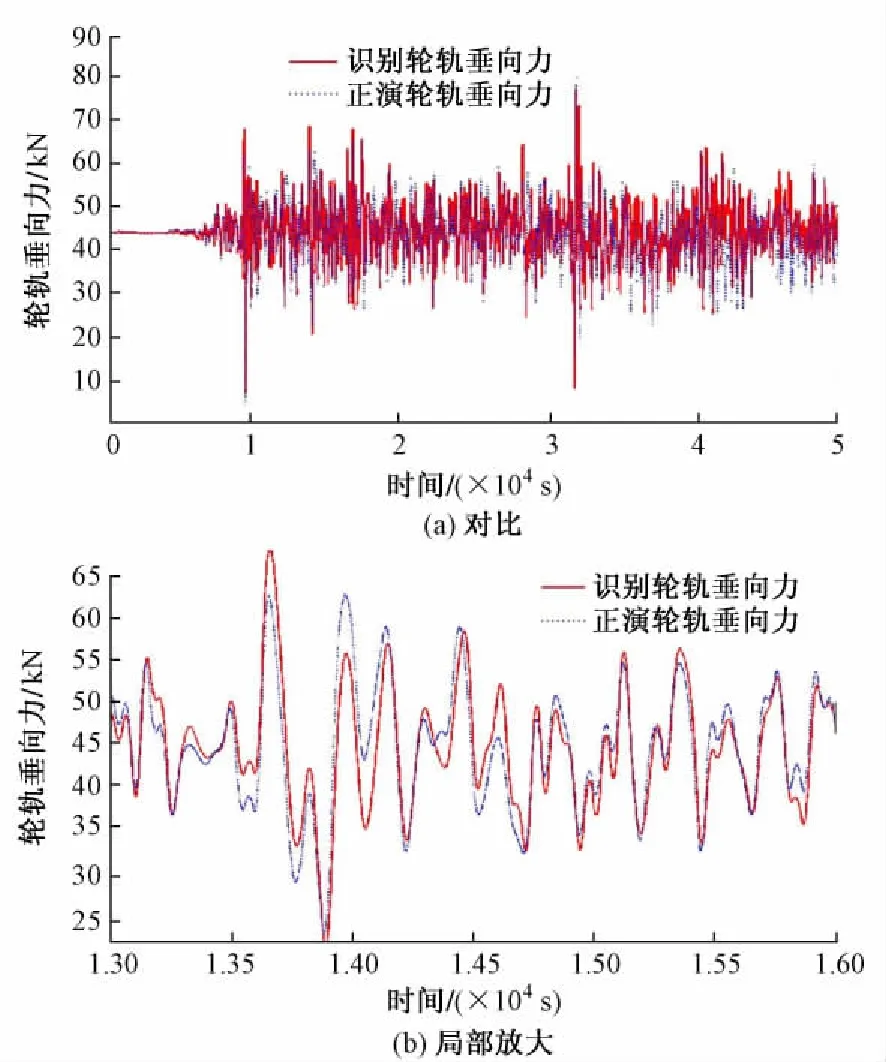
图7识别轮轨垂向力与正演模型轮轨垂向力对比

4多自由度轮轨垂向力反演模型

轮对的受力如图8所示。各符号含义如下:轮对的质量为m，侧滚转动惯量为I，侧滚角为φ;左右接触法向力分别为NL，NR;左右接触角分别为δL，δR;左右横向蠕滑力分别为FCL，FCR;左右横向力、左右垂向力分别为FL，FR，VL，VR;左右轮接触半径分别为rL，rR;左右轮接触点距轮对中心法平面的距离分别为RL，RR;左右悬挂横向力、左右悬挂垂向力分别为FSYL，FSYR，FSZL，FSZR;左右悬挂横向力、左右悬挂垂向力距轮对质心水平面、轮对质心法平面的距离分别为RSYL，RSYR，RSZL，RSZR。

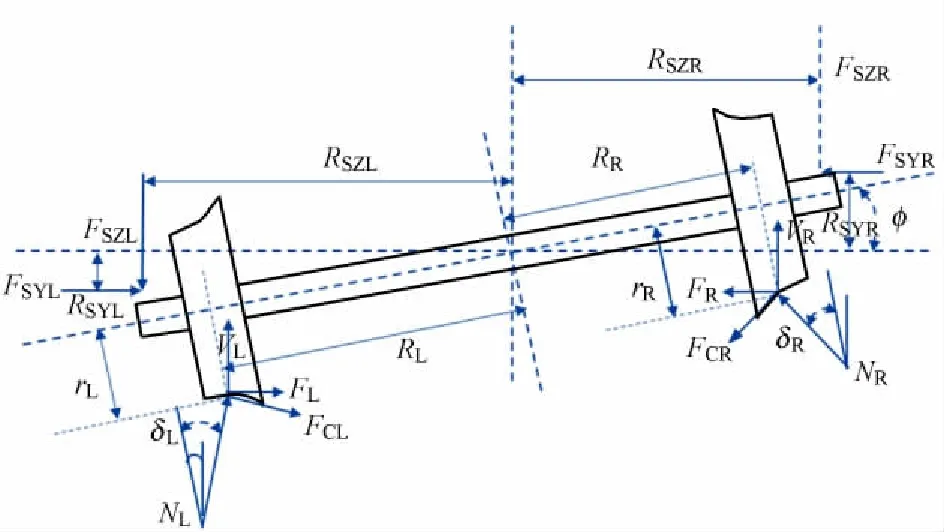
图8轮对受力分析

轮对横移的运动方程如下

考虑到便于测量等因素，把轮对质心的加速度用左右轴箱的加速度代替，即

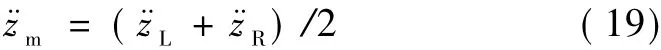
把FSZL，FSZR写成轮对和构架间的相对运动的函数，则

把式( 19)—式( 21)代入式( 18)，得

将上式改写成如下形式

同样用左右轴箱的位移、速度、加速度代替轮对的测滚角、角速度、角加速度，用左右轴箱相对于构架的位移、速度表示悬挂力，得测滚方程为

忽略测滚角对力矩产生的影响，并且假设RR，RL相差不大，rR，rL接近，则

式中: R0，r0取静平衡状态时的值。

联立式( 23)及式( 25)求解，可以精确识别出垂向轮轨力。但是在求解之前，需要求出( FR+ FL) r0的值。这可以由下式的横向运动方程求出。

首先求解式( 23)，把zL+ zR和zLB+ zRB分别看作单个自由度近似进行单自由度求解，得到VR+ VL值，如图9所示。

图9轮轨垂向力合力正与反演的结果对比放大

然后求解式( 25)，把zL－zR和zLB－zRB分别看作单个自由度近似进行单自由度求解。求解之前需要先求解式( 26)，即由式( 25)、式( 26)可以得出VR－VL值，如图10所示。

图10轮轨垂向力之差正演与反演结果对比

由VR+ VL及VR－VL的识别结果可以得出左右轮轨力的识别结果，分别如图11、图12所示。

图11左轮轨垂向力正演与反演结果对比

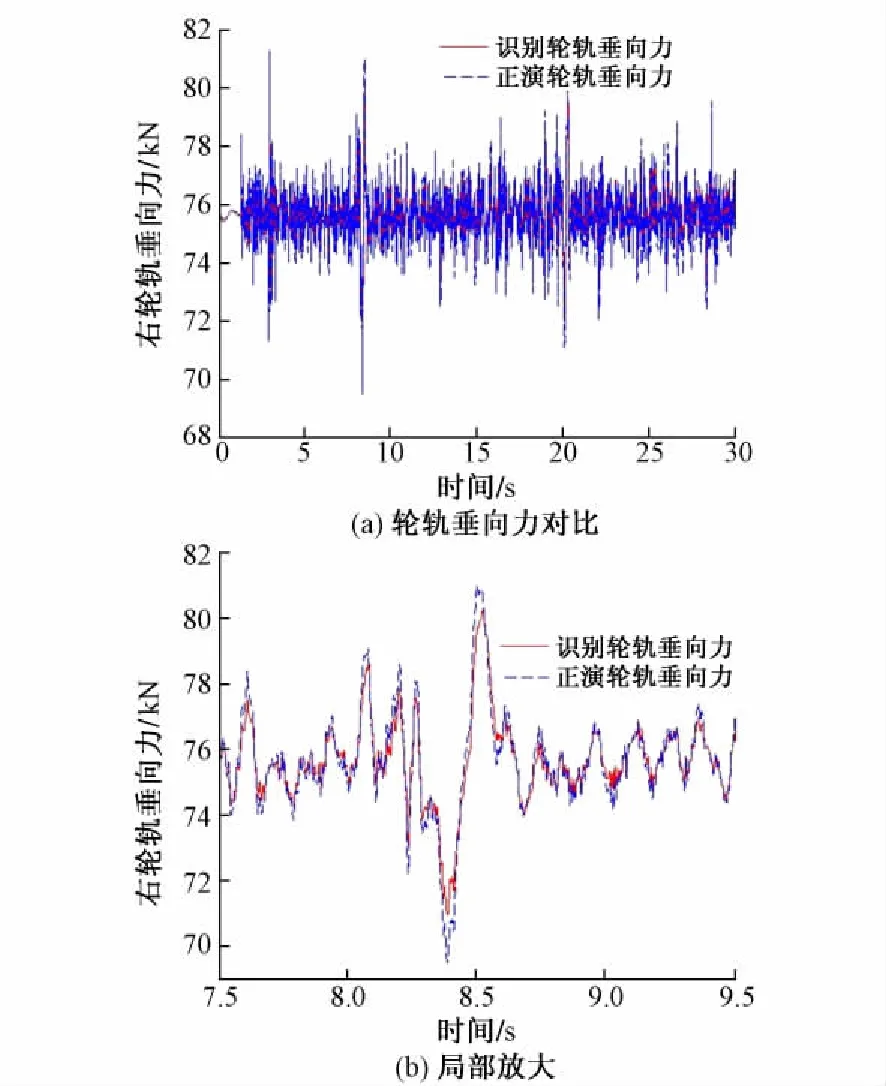
图12右轮轨垂向力正演与反演结果对比

左右轮轨力的识别结果与仿真曲线的相关系数达到0. 97，说明识别结果相当精确，可以利用该方法对轮轨力进行识别。

5　结论

1)结合车辆—轨道系统的特点，建立了单自由度轮轨力识别模型，基于杜哈密积分，在时域内推导了实时在线轮轨力识别算法，并对轮轨垂向力进行了识别，识别结果与正演模型结果相关系数达到0. 82。该方法逐点运算，可以快速高效地对轮轨垂向作用力进行识别，实时监测轮轨垂向接触力状态。

2)基于车辆动力学理论，建立了多自由度轮轨力识别模型，利用轮轨作用机理对多自由模型进行解耦。将构架加速度及轴箱加速度作为输入，对并左右轮轨力进行了识别，模型识别结果相关系数达到0. 97，具有良好的相关性。该模型把构架的响应考虑进来，显著提高了轮轨力的识别精度。

3)单自由度车轮模型较为简单，识别精度低;多自由度轮对模型较为复杂，考虑了构架的加速度，精度较高。两种模型的识别结果可以根据工程需求在不同条件下进行选用，均可在时域内对轮轨力进行实时识别。

参考文献

［1］毛玉明．动载荷反演问题时域分析理论方法和实验研究［D］．大连:大连理工大学，2010．

［2］张方，秦远田．工程结构动载荷识别方法［M］．北京:国防工业出版社，2011．

［3］蔡元奇，朱以文．基于逆向滤波器的动态载荷时域识别方法［J］．振动工程学报，2006，19( 2) : 200-205．

［4］ZHU X Q，LAW S S．Identification of Vehicle Axle Loads from Bridge Dynamic Response［J］．Journal of Sound and Vibration，2000，236( 4) : 705-724．

［5］CHEN S H，HUANG J L，SZE K Y．Multidimensional Lindstedt-poincare Method for Nonlinear Vibration of Axially Moving Beams［J］．Journal of Sound and Vibration，2007，306( 1 /2) : 1-11．

［6］朱涛，赵科，肖守讷，等．基于动态规划的动载荷时域识别方法研究［J］．振动与冲击，2012，13( 31) : 138-146．

［7］NORDSTROM L．Load Identification Using Time Domain Method［D］．Sweden: Department of Applied Mechanics，Chalmers University of Technology，2003．

［8］FURUKAWA A．A Method to Predict Track Geometry-Induced Vertical Vehicle Motion［J］．Quarterly Report of Rtri，2004，45( 3) : 142-148．

［9］FURUKAWA A．Identification of Rolling Stock Lateral Dynamic Characteristics and Their Track Irregularity Maintains Applications［J］．Quarterly Report of Rtri，2005，46 ( 1) : 7-12．

［10］UHL T．Identification of Operational Loading Forces for Mechanical Structures［C］/ /Proceeding of the 11th World Congress in Mechanism and Machine Science．Tianjin，China: 2004．

［11］UHL T．The Inverse Identification Problem and Its Technical Application［J］．Archive of Applied Mechanics，2007，77( 5) : 325-337．

［12］XIA F J，BLEAKLEY S，WOLFS P．The Estimation of Wheel Rail Interaction Force from Wagon Accelerations［C］/ /The 4th Australasian Congress on Applied Mechanics．Institute of Materials Engineering Australasia Ltd．，2005: 333-338．

［13］XIA F J，COLE C，WOLFS P．An Inverse Railway Wagon Model and Its Application［J］．Vehicle System Dynamics，2007，45( 6) : 583-605．

［14］XIA F J，COLE C，WOLFS P．Grey Box-Based Inverse Wagon Model to Predict Wheel-rail Contact Forces from Meassured Wagon Body Response［J］．Vehicle System Dynamics，2008，46( 5) : 469-479．

(责任审编李付军)

Wheel-rail vertical contact force identification based on inverse time-domain model

SUN Shanchao1，WANG Weidong1，LIU Jinzhao2

( 1．China Academy of Railway Sciences，Beijing 100081，China; 2．Infrastructure Inspection Research Institute，China Academy of Railway Sciences，Beijing 100081，China)

Abstract:Based on Dynamic Simulation，the CRH2 inspection vehicle-track model was established，and was validated by inspection data．T he results showed that the CRH2 inspection vehicle-track model was precise．W heel-rail vertical contact force and the acceleration of axle-box were simulated by using the dynamic simulation model．Based on the characteristics of the vehicle-track system，the wheel-rail vertical force identification model of single degree of freedom was established．Based on Duhamel integral，on-line W heel-rail vertical force identification algorithm was deduced．Using the simulation axle acceleration data，the vertical force was identified based on the identification model above．T he vertical identified force was compared with the simulation results．T he correlation coefficient of identified force and simulation force was 0. 82．T he identification model above identifies the force point by point，and it was efficiently．It can monitor the status of wheel and rail in time．Based on the vehicle system dynamic theory，the identification model of multiple degrees of freedom was established．Firstly，the lateral，vertical and roll motion equations were established，then some parameters were simplified．Finally，three motion equations were uncoupled．Inputting the bogie and axle acceleration to the model of multiple degrees，the vertical force were identified．T he correlation coefficient of identified force and simulation force was 0．97．T he results showed that this model was precise．T he identification model of single degree of freedom has lower accuracy than the multiple degrees model，but it is simple．T hese two models could be used according to engineering requirement．

Key words:W heel-rail vertical contact force; Force identification; M odel in time-domain; Duhamel integral

文章编号:1003-1995( 2016) 02-0121-07

作者简介:孙善超( 1979—)，男，副研究员，博士研究生。

基金项目:中国铁路总公司重点课题( 2014G009-D，2015T003-B) ;中国铁道科学研究院基金项目( 2014YJ056)

收稿日期:2015-11-09;修回日期: 2015-12-13

中图分类号:U213．2+12; U216．3

文献标识码:A

DOI:10．3969 /j．issn．1003-1995．2016．02．29