简易平面标靶下的三维扫描与数据配准

袁聪聪，张志毅

(西北农林科技大学信息工程学院，陕西 杨凌 712100)



简易平面标靶下的三维扫描与数据配准

袁聪聪，张志毅

(西北农林科技大学信息工程学院，陕西 杨凌 712100)

3D Scanning and Data Registration Based on Easy Plane Calibration Board

YUAN Congcong，ZHANG Zhiyi

摘要：为实现对物体表面三维信息的自动获取和多方位扫描结果的数据配准，提出了一种基于简易平面标靶的标定方法，并构建了相应的线激光三维扫描系统。首先，设计制作一个含有10个特征点的平面标靶，并利用平面标靶中的特征点对扫描系统进行姿态和位置标定；其次，利用平面标靶中的特征点计算其平面方程及平台平面方程；然后，在扫描时可以利用上述所得的平面方程求出激光平面方程，进而采用几何知识计算得到三维点云数据；最后，根据移动前后标靶图像上特征点信息计算出扫描系统的外部参数——平移旋转矩阵，从而可以实现多方位扫描数据的配准。试验结果表明，在距离45 cm处，几何投影变换求得的平面方程误差小于0.5%，每幅图像处理的时间小于60 ms,误差低于1.15 mm，基本满足三角测量的稳定可靠、精度高、成本低、比较适合现场标定等要求。

关键词：结构光；三维扫描；平面标靶；点云数据配准；摄像机姿态

线结构光三维扫描可实现对待测物体的非接触扫描，在逆向工程中发挥着越来越重要的作用，是获取待测目标表面轮廓信息的一种十分有效的方法，在扫描实物、建立CAD数据、检测铁轨等损坏程度及工件的形状尺寸、建立虚拟城市及虚拟农场、文物的保护与修复重建、人体建模、汽车飞机等制造业诸多领域有着很普遍的应用[1-3]。而且激光三维扫描设备在近些年逐渐向易于操作与携带、制造成本低、抗干扰性强、扫描效率高和误差小等方向发展，特别是三维打印机的产生，在众多研究领域有着很广阔的发展前景。按照激光三维扫描方式的不同，一般将激光三维扫描分为相位式、脉冲式、脉冲-相位式及三角法式4种。对于采用脉冲和相位方式的激光三维扫描仪，此类设备对激光的接收端及发射端都有着很精密的要求，一般操作十分复杂，而且携带困难，价格相对比较高。相比而言，采用三角法式的激光三维扫描的扫描原理则相对简单了很多，而且不需要价格昂贵的接收和发射仪器。

随着近年来CCD/CMOS的迅猛发展并日臻成熟，激光器结合摄像机构建而成的三维扫描系统已经实现了低成本、高精度、易于携带和操作要求的部分理论探讨和技术研发，基于三角法式的三维扫描在当今发展越来越成熟。目前国内外很多专家学者都在研究基于结合(单目、双目、多目)摄像机和激光器的激光三维扫描系统的构建原理和实现方法，其中有很多值得学习和借鉴的地方。一般的，每次扫描只能得到所测物体单侧表面离散点集的空间坐标信息，人们将这些坐标信息称为点云数据信息。当要获得目标整体的三维坐标数据时，通常采用平移和旋转的扫描方式来实现[4]。扫描系统在挪动之后进行再次扫描所获得的数据，会因为与首次扫描的基准点和基准平面不统一而需要数据配准。为解决该问题，需要获得每次扫描相对于首次扫描基准点和基准平面的位置和姿态信息。通常为获得这些姿态信息需要借助高精度的辅助设备(如惯导系统和陀螺仪)，这既增加了系统设计的成本，还增加了系统校准的难度及计算的复杂度。文献[5—6]介绍了一种基于图像的标定方法，但是其标定板和标定算法都很复杂，时间复杂度不好。文献[7—8]也给出了一种激光三维扫描系统的设计，扫描精度高，但是所需设备成本太高。为了降低算法设计和系统校准的复杂度，以及设计成本，本文提出了一种手持式操作简单、误差小的设计方案——基于平面标靶的线激光三维扫描系统的构建和姿态标定，只需一些特征点就可以进行系统的标定和扫描结果的计算，以及半球空间内360°自由配准。

一、三维扫描原理

本文采用三角法式三维扫描，此算法利用三角形几何关系，计算获得观测点到被测对象的距离。

1. 系统设计

试验中采用一种线激光器，线激光器发射一束激光到物体表面上，由于表面的不同几何形状，激光条会发生变形而出现在摄像机视野的不同位置，然后利用摄像机获取含有激光光条的待测对象图像。物体表面的激光光条中心的各点、摄像机中心及激光源原点组成一系列三角形，此技术称作三角法式测距[9]。图1为三维激光扫描系统构造原理。从图1可以看出，三维激光扫描装置一般包含激光发射设备、摄像机、被测物体及参照物试验台等。

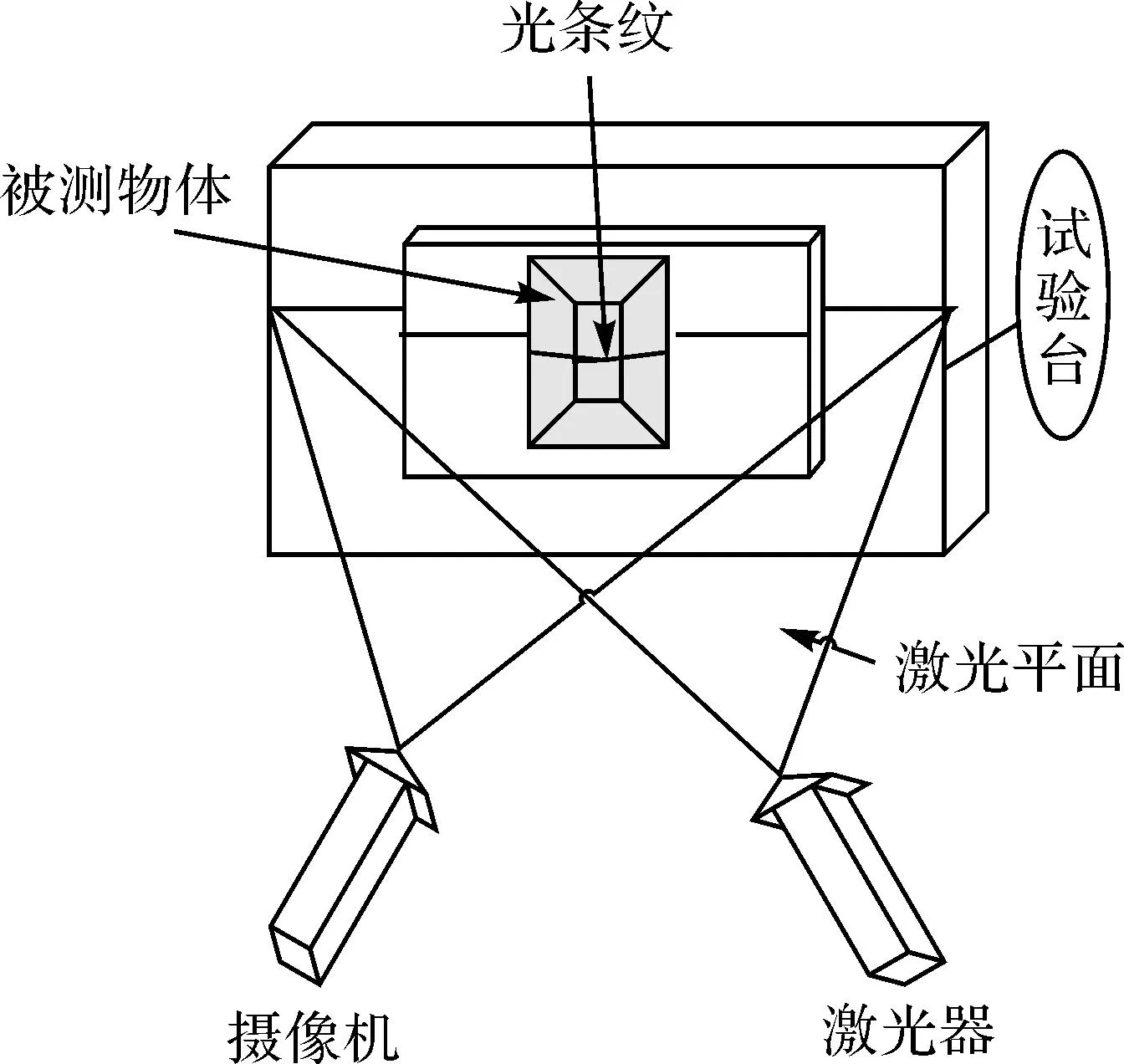
图1　三维激光测量原理

作为激光三维扫描系统最基本的构造，扫描过程中激光源在物体上留有激光条纹，摄像机获取含有激光条纹的目标对象图像，之后计算出图像中光条中心，最后采用一系列几何计算得到待测对象在空间中的坐标信息。

2. 标定板设计

为了能够更好地设计系统的位置和姿态的标定，在本研究中设计了如图2所示的平面标靶，在平面标靶中可以看到有主要的4个黑圆圈，以及周围一些相对较小的黑圆圈。

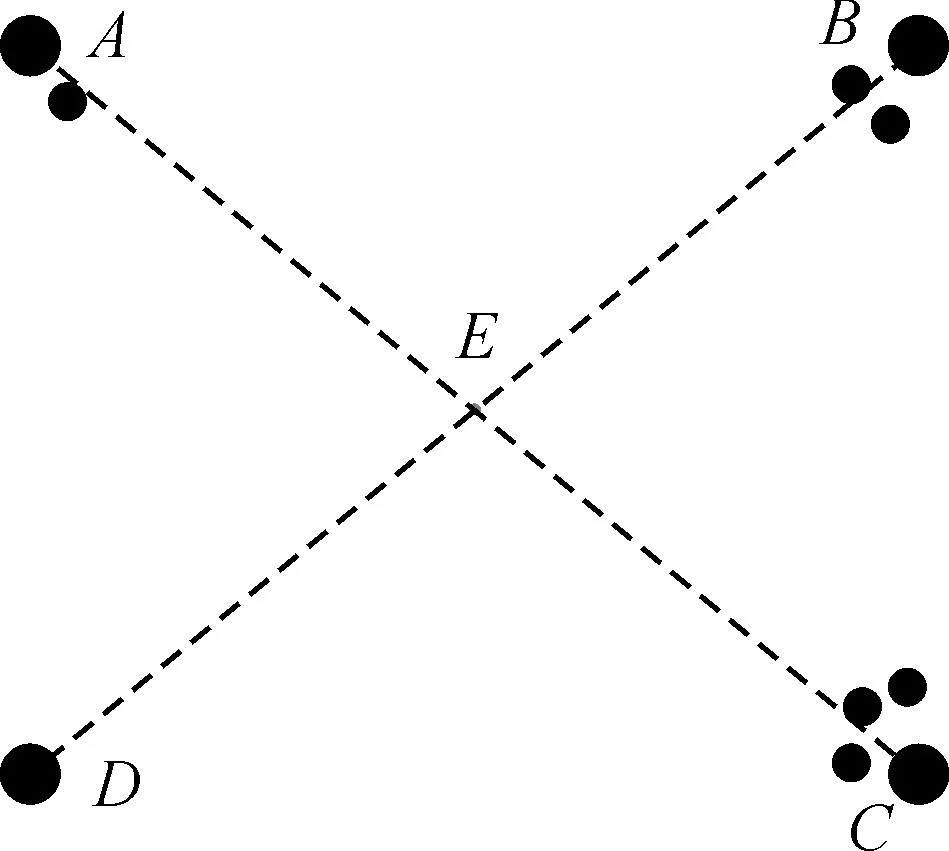
图2　平面标靶

为了更好地描述本文的标定算法，在图2中的平面标靶上加入了主要点的表示符号A—E，以及两条对角线。其中A—D位于矩形的4个顶点，E为AC和BD的交点。A—E5个点主要用于计算平面标靶的平面方程、试验平台的平面方程及激光平面方程，而其余相对较小的点主要用于标记系统姿态。以主点周围小点的数目0—3来表示4个方位，因此能够方便地获取扫描系统的位置姿态。

摄像机获取平面标靶的图像信息，求出标定板中的特征点，利用最小凸包算法求得本文所要使用的A—D4个主点，以及它们旁边小点数目可以用来标记摄像机姿态。本文采用文献[10]提出的几何投影变换算法求解A—E5个点的空间坐标。

如图3所示是一个平面标靶上特征点A、C、E的成像模型。E为AC的中点，O为摄像机光心，A′、C′、E′为A、C、E的投影点，其中E′是虚拟的，是平面标靶上A—D在投影平面上的投影A′C′与B′D′的相交位置点。需要通过两直线相交的原理求出E′。设AE=CE=d，距离d的值已知，O到投影平面的距离即为焦距f，A′、C′、E′的坐标根据提取图像特征点可以得知。设坐标A=t1·A′,C=t2·C′,E=t3·E′,因为E是AC的中点，可得出t3=(t1+t2)/2。因此根据透视投影几何原理，可以得到

图3　几何投影变换

(1)

式(1)只有t1、t2、t3是未知的，因此3组方程加上1个辅助方程可以求出唯一解t1、t2、t3，又因为A=t1·A′,C=t2·C′,E=t2·E′, 因此可求出A、C、E3点相对于摄像头中心原点的空间位置坐标值。同理求出B、D的空间位置坐标值。至此能够计算出平面标靶上的4个主要点A—D相对于摄像机中心的空间坐标，因此利用空间4点最小二乘法平面拟合的算法求出平面标靶的方程。令空间平面方程为

Ax+By+Cz+1=1

(2)

由式(2)可以得出平面法向量n=(A,B,C)。设测量点Pi(xi,yi,zi)，点Pi到拟合平面的有向距离为di=nPi+1,根据最小二乘法原理，S=∑di2要最小，因此用S分别对A、B、C求偏导，得出3组三元一次方程

(3)

由式(3)可以求出平面标靶的平面方程，记为方程F(P)。

3. 激光平面标定

在计算激光平面方程的时候，需要借助一个平台，此平台与平面标靶平行，平台平面与平面标靶平面的距离为m已知，因此利用两平面平行及已知其中一平面的方程和两平面的距离可以求出另一个平面的方程[10]，因此，由平面标靶平面方程F(P)和距离m可以求出平台平面方程，记为方程F(P′)。激光平面的求解如图4所示。

图4　激光平面标定

在图4中，激光条纹分别落在物体、平面标靶及辅助平台上，在平面标靶和辅助平台上分别找到激光条中心上的两个点，如图4中的光条上的4个黑色点，然后利用平面标靶的平面方程F(P)及辅助平台平面方程F(P′)求出这4个点的空间三维坐标，最后利用式(2)、式(3)最小二乘法拟合平面的方法求出激光平面方程。为了能够以很小的误差求出激光平面方程，必须准确计算出光条中心点。

4. 半球空间内360°点云配准

三维旋转和平移配准是本文的一个重要研究内容，因为要把所有三维坐标在一个坐标系下表示，因此假设摄像机初始位置的摄像机坐标系为世界坐标系，然后在摄像机和扫描仪移动过程中，将其他姿态下获得的数据信息计算到世界坐标系，这就需要三维旋转和平移配准。其中通过一次移动之间获得的两个标定板上的标定点，通过标定点之间的几何关系，解方程组可求得平移和旋转参数。本文采用姚吉利提出的一种方法——三点法计算转换参数[11]，转换过程如下

(4)

式中，等号左侧是目标坐标下的坐标；等号右边(下标为S)为原坐标；λ为尺度因子，表示两坐标系统上的单位大小之比;R为旋转矩阵;[ΔXΔYΔZ]T为平移向量。

已知基本转换过程及平面标靶平移旋转前后两次标定点A—D4个点的空间坐标，采用文献[7]三点法计算转换参数，即可计算出旋转矩阵及平移矩阵。其中从4个标定点中取3个作为配准点，这样能够得到4组，把求解得到的结果求平均值。在此，以初始摄像头中心位置为世界坐标系，之后在扫描移动过程中要把目标物体上的点云数据全部统一到世界坐标系下。

5. 摄像机标定

在三维扫描中，标定摄像机是一个不可缺少的关键因素。摄像机标定在计算机视觉研究领域占有十分重要的地位，是很多研究问题的前提，目的是计算出摄像机的内外参数。外部参数描述摄像机在外界空间中的方向和位置，内部参数主要描述摄像机本质的光学和几何特性。通过构建相应的数学几何模型，计算出世界坐标系与图像坐标系之间的几何映射模型，最后能够高效地求解得到摄像机内外参值。常用的标定算法主要有张正友所设计的标定算法[12]和基于一阶径向畸变的Tsai标定算法[13-14]。这两种标定过程比较难以控制，计算复杂，因此本文采用了文献[10]设计的一种比较简单易于控制的标定算法。此标定算法需要一个类似棋盘格性质的人工参照物，而本文所设计的简易标定板正好适用于此算法的摄像机标定。

二、测量试验与结果

上节描述了三维扫描的原理，根据这些扫描方法，在微软的Windows 7操作系统下采用VS2008进行程序开发，开发语言是C/C++及OpenCV 2.4版本的图像处理库。采用罗技Pro9000摄像机及650 nm的5 mw一字线激光笔，自制平面标靶并构建试验平台。

1. 扫描过程

如图5所示，扫描系统首先支在扫描物体的一个方向，然后手持激光器上下扫描物体，在物体上显现激光条纹，摄像机拍摄含有激光条纹的目标对象。

图5　三维扫描系统

接着对激光条纹中心点进行计算，求解光条中心的计算方法为灰度重心法[10,15-18]，计算出光条在第k列的中心点，采用跟踪法计算第k+1列，即在第k列中心点的基础上的一定范围内进行搜索。摄像机光心和提取的成像平面上光条纹中心的任一点可确定一直线，此直线与上节所求的激光器投射的激光平面相交于一点，利用已知直线方程和平面方程相交的几何关系，求解得到的交点就是物体表面相应点的三维坐标值。

通过上述求解方法可以计算出待测量物体的表面三维坐标集合，设为点云P1{p1,p2, …}。然后将扫描系统变换到其他方位进行扫描，连续变换3次，得到物体表面三维坐标集合分别为点云P2{p1,p2, …}，P3{p1,p2, …}，P4{p1,p2, …}，就可以在4个方位完成整个物体扫描。最后利用前面所介绍的点云配准，将P2、P3、P4经过平移旋转到P1所在的坐标系下得到物体完整的点云数据，即可完成半球空间内360°点云数据配准，重建时对冗余数据进行处理即可。

2. 点云配准参数

RT1、 RT2、 RT3分别是逆时针旋转平移3次后所求的旋转平移矩阵，采用上小节的算法进行求取结果，所得到的结果如下

3. 系统扫描精度分析

在平面标靶上，AB=CD=236.5 mm，AD=BC=174.5 mm,在系统中主要用到的几何投影变换方法得到的结果见表1，其中d1、d2、d3、d4表示AB、BC、CD、AD计算出来的长度，EA表示最大绝对误差,ER表示最大相对误差。

表1　投影变换法标定结果

表1中的3组标定数据，在距离45 cm处扫描最大绝对误差为1.15 mm，相对误差小于0.5%，标定点的精确度决定了整个系统的扫描精度。

4. 扫描结果

使用本文所述方法开发的三维扫描系统在室内扫描了一个兵马俑模型。图6是待扫描原始模型，图7显示扫描的结果，在位置1处显示图像共有14 879个数据点，在位置2处有13 765个数据点，在位置3处有13 843个数据点，在位置4有13 276个数据点。

图6　原图像

三、结束语

本文提出了一种基于简易平面标靶的线激光三维扫描的姿态标定，以及利用标定板上的特征点计算三维坐标的完整方法，改进了标定板设计的复杂度及点云配准的难度。经过几何投影变换求解平面标靶的平面方程的精度最大相对误差小于0.5%，通过借用平面标靶与试验台这两个平面，实现了一种快速的激光平面求解算法。利用平面标靶标定扫描系统的位置和姿态的方法，能够简单快速地进行半球空间内360°点云配准，具有很高的应用价值。试验表明，在距离45 cm处扫描最大绝对误差为1.15 mm，相对误差小于0.5%，每幅图像的处理时间少于60 ms,操作简单，稳定可靠，并且使硬件成本大大降低，比较适合现场标定。

图7　扫描结果图像

参考文献：

[1]周森,郭永彩,高潮.基于三维激光扫描的移动大尺寸圆柱体工件长度快速检测系统[J].光学精密工程,2014,22(6): 1524-1530.

[2]劳达宝,杨学友,邾继贵，等.扫描平面激光坐标测量系统校准方法的优化[J]. 光学精密工程,2011,19(4): 870-877.

[3]田庆国,葛宝臻,杜朴，等.基于激光三维扫描的人体特征尺寸测量[J]. 光学精密工程，2007,15(1):84-88.

[4]吴庆阳，李景镇，苏显渝，等.线结构光三维测量系统中旋转轴的标定方法[J].中国激光，2008,35(8):1224-1227.

[5]曾祥军，霍金成，吴庆阳.线结构光三维测量系统扫描方向的标定[J].中国激光，2012,39(1):1-5.

[6]袁建英，郭进，王玮，等.一种结构光三维扫描系统新标定方法[J].计算机应用与软件，2013,30 (3):151-153.

[7]TIAN Qingguo, YANG Yujie, ZHANG Xiangyu，et al. An Experimental Evaluation Method for the Performance of a Laser Line Scanning System with Multiple Sensors [J]. Optics and Lasers in Engineering,2014, 52(1):241-249.

[8]LI Xudong, ZHAO Huijie, LIU Yang, et al. Laser Scanning Based Three Dimensional Measurement of Vegetation Canopy Structure[J]. Optics and Lasers in Engineering, 2014,54(1):152-158.

[9]EMAM S M, KHATIBI S, KHALILI K. Improving the Accuracy of Laser Scanning for 3D Model Reconstruction Using Dithering Technique[J]. Procedia Technology, 2014,12(1): 353-358.

[10]ZHANG Zhiyi, YUAN Lin. Build a 3D Scanner System Based on Monocular Vision[J]. Applied Optics, 2012,51(10):1638-1644.

[11]姚吉利.3维坐标转换参数直接计算的严密公式[J].测绘通报，2006(5):7-10.

[12]ZHANG Z．A Flexible New Technique for Camera Calibration[J]．IEEE Transactions on Pattern Analysis and Machine Intelligence，2000，22(11)：1330-1334.

[13]TSAI R Y. An Efficient and Accurate Camera Calibration Technique for 3D Machine Vision[C]∥IEEE Conference on Computer Vision and Pattern Recognition. Miami Beach: [s.n.], 1986:364-374.

[14]TSAI R Y. A Versatile Camera Calibration Technique for High-accuracy 3D Machine Vision Metrology Using Off-the-shelf TV Cameras and Lenses[J]. IEEE Journal of Robotics and Automation,1987,3(4):323-344.

[15]LV Zhihua, ZHANG Zhiyi. Build 3D Scanner System Based on Binocular Stereo Vision[J]. Journal of Computers, 2012,7(2):399-404 .

[16]孙军华，王恒，刘震，等. 钢轨磨耗动态测量中激光光条中心的快速提取[J].光学精密工程，2011,19(3):691-694.

[17]王建文，杜春梅．激光三维扫描图像处理改进算法[J].计算机工程与设计，2010.31(17):3929-3931.

[18]江洁，邓珏琼，张广军，等．光条纹中心的实时快速提取[J] .光学技术，2008，34(2):170-174.

中图分类号：P237

文献标识码：B

文章编号：0494-0911(2016)02-0050-05

作者简介：袁聪聪(1988—)，女，硕士，研究方向为计算机图形学。E-mail: 840386719@qq.com

基金项目：国家高技术研究发展(863)计划(2013AA10230402);中央高校基本科研业务费西北农林科技大学科技创新项目(QN2013054)

收稿日期：2015-03-24

引文格式： 袁聪聪，张志毅. 简易平面标靶下的三维扫描与数据配准[J].测绘通报，2016(2)：50-54.DOI:10.13474/j.cnki.11-2246.2016.0047.