竞争环境下基于服务约束的轴-辐式海运网络优化研究

赵宇哲, 周晶淼, 匡海波

(1.大连海事大学综合交通运输协同创新中心, 辽宁 大连 116026;2. 大连理工大学管理与经济学部, 辽宁 大连 116023)

竞争环境下基于服务约束的轴-辐式海运网络优化研究

赵宇哲1, 2, 周晶淼2, 匡海波1

(1.大连海事大学综合交通运输协同创新中心, 辽宁 大连 116026;2. 大连理工大学管理与经济学部, 辽宁 大连 116023)

针对同一海运市场中不同的海运企业——领导者与跟随者在设计多分配的轴-辐式海运网络时引起的竞争问题，突破已往枢纽港口集合是给定的假设，将航线连接设计扩展为可存在多条，引入基于服务约束(服务质量价格时间)的吸引力模型来定量表示托运人的选择行为，建立了竞争环境下基于服务约束的轴-辐式海运网络优化问题的数学模型，利用NCP函数、凝聚函数和增广Lagrange乘子罚函数法对这一问题进行求解。算例仿真结果显示：(1)跟随者在托运人考虑单位服务价格时，即使不存在规模经济效应，跟随者也可通过建立合适的枢纽港口来获取一定的市场机会；(2)跟随者在存在较大规模经济效应时其利润最可观，因采用比例模型，在不存在规模经济效应下跟随者在领导者决定设计不同数量的枢纽港口时其利润不会统一收敛于某一定值；(3)跟随者在领导者仅设计1个枢纽港口时可通过建立大量的枢纽港口来争夺丰厚的利润，但对于港口集合N={1,2,…,12}的海运市场，领导者只需设计2个以上枢纽港口时跟随者的利润空间便会受到较大挤压。

轴-辐式网络；竞争；服务约束；连续化方法；增广Lagrange乘子罚函数法

1 引言

目前，全球贸易货量的80-90%是通过海上运输这一国际运输通道进行的，Held等的《全球化大变革：全球化时代的政治、经济与文化》确定了高效的运输系统是经济全球化的重要基础，但是全球化研究中有关海上运输的重要性却被忽视了[1]。过去三十年，海上运输持续增长，年平均增长率为3.1%，运输需求的增长直接导致了海运市场上运力供给的快速增长[2]。海运企业作为海运市场的主体，每个国家都在大力扶植海运业、鼓励本国的海运企业积极参与国际竞争，这导致了国际海运市场的竞争十分激烈[3]。为争夺更多的利润和市场份额，一些大型海运企业(马士基、地中海、达飞等)倾向于通过横向的兼并、重组、联盟等来实现市场扩张与航区覆盖，建立起来的海运联盟(伟大联盟、P3联盟和CKYH联盟等)可采取运价协定、货载分配协定、共同分配、控制竞争等对内措施与回扣制度、联运协定等对外措施来消除竞争，控制海运资源以排挤其它海运企业[4]，这使得一些运营规模较小或新进入市场的海运企业正逐步丧失它们的利润和市场份额。海运网络是海运企业提供海上运输服务的运营基础[5]，对于新进入市场的中小型海运企业而言，为争夺更多的或者至少恢复已经丧失的利润和市场份额，如何设计能与大型海运企业(或海运联盟)相竞争的海运网络至关重要。

由于海上运输的服务需求派生于全球经济增长的需要，轴-辐式网络凭借其符合全球贸易格局的结构特性和规模经济效应，能够大幅减少船舶运营成本、船舶运营数量，提高船舶负载率、船舶利用率，已成为全球海运系统中最重要的网络形态[6]。轴-辐式网络，根据枢纽节点的个数可分为单枢纽和多枢纽网络，每个非枢纽节点只能与一个枢纽节点相连接的多枢纽网络称为单分配的轴-辐式网络；存在连接多个枢纽节点的多枢纽网络称为多分配的轴-辐式网络[7]。由于多分配的轴-辐式网络可根据海运需求的多样性、市场竞争的加剧等因素灵活分配于枢纽港口中转并进行设计相应的航线连接，因此，它比单分配的轴-辐式网络具有明显的竞争优势，但其组织形式也更为复杂。

轴-辐式网络优化问题的研究主要集中于不同类型的枢纽选址模型设计：P-Hub中心问题、P-Hub中位问题和P-Hub(最大、集)覆盖问题等。Campbell和O’Kelly[8]、Alumur和Kara[9]、Klincewicz[10]和Faharani等[11]对枢纽选址模型作出了深入的系统性评述。当前，枢纽选址模型的研究趋势在于开发新的构想并赋予其更多的现实基础，沿着这个方向已经有很多研究进行了多面性的探讨：折扣流量问题、枢纽容量问题和动态选址问题等，但研究中仍有两方面关注比较少：竞争与轴-辐式网络在海运的应用。关于具有竞争性的枢纽选址模型研究中，Marianov等[12]第一个针对出现在客运和货运中的竞争问题进行了枢纽选址优化，将现存企业称作领导者、新进入市场企业称作跟随者，构建的竞争原则是提供运输服务收入的增加，研究结果表明跟随者若想进入市场需通过设计新的枢纽和降价方式促使客户改变选择以最大化其经济收入。Gelareh等[13]基于费用/时间的吸引力等因素，通过设计一个竞争环境下的枢纽选址模型用于制定市场中跟随者的竞争策略。赵宇哲[14]在Gelareh等[13]研究的基础上，通过引入基于服务成本/时间的吸引力模型，评估了市场中跟随者对客户需求(服务成本/时间)多样性的竞争策略，结果显示若领导者决策不能与跟随者同步，则其市场份额将会受到威胁。但是，上述枢纽选址模型均是离散型的，即选址的枢纽节点数量是给定的，忽视了枢纽节点确定的内生性问题。关于轴-辐式网络在海运的应用研究中，陈康等[15]基于多港挂靠和轴-辐式网络的混合结构，构建了可确定干线靠泊港口及靠泊顺序、支线港口以及空重箱运输方案的海运网络优化模型。Zheng Jianfeng等[16]构建了考虑时间因素二阶段的轴-辐式海运网络优化模型，讨论了沿海运输权对班轮运输网络设计成本的影响。赵宇哲等[17]考虑了集装箱OD需求的不确定性对海运网络设计的影响，构建了不确定OD需求下的轴-辐式海运网络优化模型。但是，上述轴-辐式海运网络优化模型均只适用于单一航线连接设计问题，即每一个起讫港口之间的航线连接有且仅有一条，这与现实不尽相符，当轴-辐式海运网络优化由单一航线连接设计问题演变为多条航线连接设计问题时，其复杂度将大大增加。

海运市场的跌宕起伏直接影响着海运企业的盈利能力。尽管海运市场是一个具有寡头垄断特点的市场，但也遵循着一般的市场经济规律，即其提供的海运服务对托运人是否具有吸引力。关于吸引力模型的研究可追溯到Reilly[18]提出的确定性模型，接着Huff[19]延伸了Reilly[18]的吸引力模型的思想，提出从客户的选择行为出发，基于提供服务的便利性构建了客户的吸引力模型。之后，Marianov[12]将吸引力模型运用至具有竞争性的枢纽选址模型中。Eiselt等[20]拓展了Marianov等[12]的研究，将枢纽选址模型设计为综合时间、费用和吸引力的效用函数最大化的非线性模型。上述吸引力模型中，托运人的选择行为起到至关重要的作用，但现实中托运人的选择行为比较抽象，如何将其定量表示且与海运企业的轴-辐式海运网络优化问题相联系是一个难点。

鉴于上述分析，本文根据不同海运企业在海运市场中的地位，将现存的大型海运企业称作领导者，将新进入市场的中小型海运企业称作跟随者，以多分配的轴-辐式网络作为两者运营的基本网络结构，突破已往枢纽港口集合是给定的假设，将航线连接设计扩展为可存在多条，引入基于服务约束(服务质量价格时间)的吸引力模型定量表示托运人的选择行为，基于此，建立竞争环境下基于服务约束的轴-辐式海运网络优化模型；利用NCP函数、凝聚函数和增广Lagrange乘子罚函数法对这一问题进行求解。最后，通过算例仿真分析不同情境下跟随者基于服务约束的轴-辐式海运网络优化问题，为跟随者参与海运竞争提供可验证的决策参考。

2 问题描述

竞争环境下基于服务约束的轴-辐式海运网络优化问题可描述为：假设存在一个海运市场覆盖的港口集合N={1,2,…,n}，任一港口u,v(v≠u)∈N；Fu表示任一港口u的投资成本，Cuv和Cu分别表示任意两个港口u、v之间的单位运输价格与任一港口u上的单位中转价格，同理，Tuv和Tu分别表示任意两个港口u、v之间的单位运输时间与任一港口u上的单位中转时间；Qij(j≠i)表示海运市场上的非弹性需求，为起点港口i∈N到讫点港口j∈N的OD流量。目前，海运市场由现存的大型海运企业A(领导者A)通过设计的轴-辐式海运网络GA=(N,VA)运营，其中，港口集合N=HA∪SA，HA表示枢纽港口集合，SA表示非枢纽港口集合，航线连接集合VA={(uA,vA)|uA,vA∈N,uA≠vA}；考虑到规模经济效应，α∈(0,1]表示枢纽港口kA,lA∈HA之间单位运输价格的折扣因子。领导者A设计的轴-辐式海运网络GA是在满足所有海运需求∑i,j∈NQij的基础上，由pA个枢纽港口kA完全连接的运营网络，基于航线连接集合VA提供于托运人的单位服务价格为CijkAlA和单位服务时间为TiijkAlA。对于一个新进入市场的中小型海运企业B(跟随者B)，为同一港口集合N服务，需在调查所有海运需求∑i,j∈NQij的基础上，在投资成本Fu、单位运输价格Cuv/时间Tuv、单位中转价格Cu/时间Tu固定的情况下设计符合自身优势的轴-辐式海运网络GB=(N,VB)，从领导者A提供于托运人的OD流i→j上争夺一定流量以实现其利润最大化。其中，港口集合N=HB∪SB，航线连接集合VB={(uB,vB)|uB,vB∈N,uB≠vB}，折扣因子α等与轴-辐式海运网络GA类同，跟随者B可选择与领导者A相同的港口作为枢纽港口，但不与领导者A共享枢纽港口。因此，为迅速争取在某些OD流i→j上的市场机会，跟随者B应解决的问题有：(1)在单位运输价格Cuv/时间Tuv、单位中转价格Cu/时间Tu与领导者A相同的情况下，可否获得利润？(2)枢纽港口的数量pB和枢纽港口kB∈HB的选址情况是什么？(3)基于枢纽港口kB的航线连接集合VB是什么？

3 模型分析

3.1 OD流i→j上的航线连接集合

对于跟随者B，进入已知存在的海运市场时，所有港口N={1,2,…,n}的位置已知，轴-辐式海运网络GB设计的关键在于确定哪些港口是枢纽港口HB(剩余港口自然是非枢纽港口SB)以及枢纽港口HB与非枢纽港口SB之间、枢纽港口HB之间的航线连接集合VB。轴-辐式海运网络GB=(N,VB)属于多分配的轴-辐式网络，非枢纽港口SB可分配给多个枢纽港口HB，但中转只可在枢纽港口HB进行。因此，起讫港口i,j之间OD流i→j上的航线连接上枢纽港口一般不超过2个，即任一航线连接只可能是2、3或4个港口[14]，则有2个港口的航线连接：(i,j)∈HB×HB∪HB×SB∪SB×HB；3个港口的航线连接：(i,kB,j)∈SB×HB×HB∪SB×HB×SB∪HB×HB×SB；4个港口的航线连接：(i,kB,lB,j)∈SB×HB×HB×SB。已往起讫港口i,j之间OD流i→j上的航线连接设计具有唯一性，针对这一不尽合理的假设，将跟随者B在OD流i→j上的航线连接设计扩展为可存在多条，即允许上述2、3或4个港口的航线连接的不同组合作为轴-辐式海运网络GB中OD流i→j上的航线连接集合。

3.2 基于服务约束的吸引力模型

由于存在的海运市场覆盖的港口集合N={1,2,…,n}已知且固定，托运人在起讫港口i,j之间OD流i→j上选择不同海运企业(领导者A与跟随者B)提供的服务时，基于随机效用理论，托运人在特定条件下一般会选择其所认知方案中效用最大的方案。随着海运服务的同质性不断趋强，托运人在选择不同海运企业提供的服务时主要考虑三个因素：一是基于枢纽港口之间运输的服务质量Θkl，涉及到安全性(航行条件等)和便利性(港口地理位置等)；二是基于航线连接的单位服务价格Cijkl，有Cijkl=(Cik+αCkl+Clj)+(Ck+Cl)；三是基于航线连接的单位服务时间Tijkl，有Tijkl=(Tik+Tkl+Tlj)+(Tk+Tl)。可见，单位服务价格Cijkl/时间Tijkl主要取决于起讫港口i,j之间OD流i→j上的航线连接设计。鉴于吸引力模型常用于行为选择分析且已在运输领域的一些著作中被充分验证[21-23]，区别于已往二元离散选择模型，建立不同海运企业提供任一航线连接的吸引力模型有：

(1)

其中β和γ为一组关于单位服务价格Cijkl/时间Tijkl的灵敏系数，表示吸引力Uijkl的减少速度与单位服务价格Cijkl/时间Tijkl的增加速度是一致的；θ和(1-θ)为一组关于单位服务价格Cijkl/时间Tijkl的权重系数。

4 模型建立

4.1 基本假设

假设1轴-辐式海运网络的结构相对稳定，不考虑灾害、战争等突发状况对海运企业运营网络的影响。

假设2轴-辐式海运网络中任意两个港口之间使用的船型已知，且有足够的船舶运力提供服务。

假设3轴-辐式海运网络中枢纽港口之间运输的规模经济效应即单位运输价格的折扣因子α已知。

假设4轴-辐式海运网络中所有OD流i→j的流量Qij，任意两个港口之间的单位运输价格Cuv/时间Tuv和单位中转价格Cu/时间Tu已知且固定。

假设5领导者A设计轴-辐式海运网络GA的枢纽港口HA和航线连接集合VA已知。

4.2 决策变量

ykB为枢纽港口的选择变量。若任一港口被选择为枢纽港口，则ykB=1，否则ykB=0。

xijkBlB为起讫港口i,j之间OD流i→j上航线连接的选择变量。若存在4个港口的航线连接(i,kB,lB,j)，则xijkBlB=1，否则xijkBlB=0；若存在3个港口的航线连接(i,kB,j)，则xijkBlB=1，否则xijkBlB=0；若存在2个港口的航线连接(i,j)，则xijkBlB=1，否则xijkBlB=0。

4.3 数学模型

竞争环境下基于服务约束的轴-辐式海运网络优化问题相应的数学模型有

maxZ(xijkBlB,ykB)=∑i,j,kB,lB∈NQij

CijkBlBPijkBlB-∑kB∈NFkBykB,

(2)

s.t.∑kB,lB∈NPijkBlB+∑kA,lA∈HAPijkAlA=1, ∀i,j∈N,

(3)

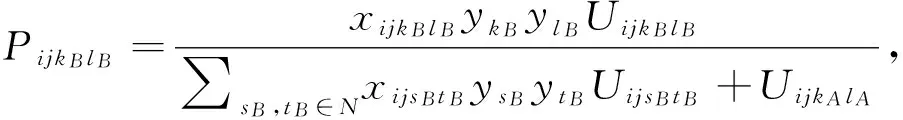
(4)

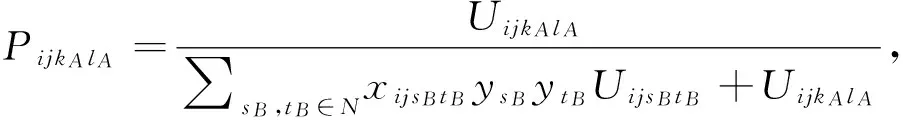
(5)

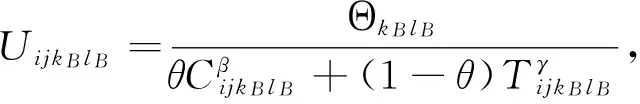
(6)

(7)

CijkAlA=CikA+αCkAlA+ClAj+CkA+ClA, ∀i,j∈N, ∀kA,lA∈HA,

(8)

CijkBlB=CikB+αCkBlB+ClBj+CkB+ClB, ∀i,j,kB,lB∈N,

(9)

TijkAlA=TikA+TkAlA+TlAj+TkA+TlA, ∀i,j∈N, ∀kA,lA∈HA,

(10)

TijkBlB=TikB+TkBlB+TlBj+TkB+TlB, ∀i,j,kB,lB∈N,

(11)

xijkBlB,ykB∈{0,1}, ∀i,j,kB,lB∈N.

(12)

目标函数(2)为跟随者B设计轴-辐式海运网络GB的利润最大化，即其从领导者A的轴-辐式海运网络GA中OD流i→j上争夺一定流量带来的收入减去其在枢纽港口kB的投资成本。约束(3)表示起讫港口i,j之间OD流i→j同时经过跟随者B与领导者A的枢纽港口，由跟随者B与领导者A以竞争方式共同分担起讫港口i,j之间的OD流量；约束(4)-(5)为跟随者B与领导者A对应于起讫港口i,j之间OD流i→j上某一航线连接的比例函数PijkBlB和PijkAlA，即基于服务约束的吸引力模型UijkBlB和UijkAlA，托运人分配给跟随者B与领导者A的OD流量比例；约束(6)-(7)为跟随者B与领导者A提供于托运人任一航线连接的吸引力模型；约束(8)-(11)为领导者A与跟随者B提供于托运人任一航线连接的单位服务价格CijkAlA和CijkBlB/时间TijkAlA和TijkBlB；约束(12)表示跟随者B决策变量为0-1示性变量。可见，模型(2)-(12)是一个连续型的枢纽选址模型，即选址投资的枢纽港口数量pB是内生的，将其作为枢纽港口选址HB与航线连接集合VB决策方案的一部分来确定的。

5 模型求解

5.1 基于NCP函数的连续问题

模型(2)-(12)是一个非线性0-1优化问题，这一类问题求解的精确算法(隐枚举法、分支定界法等)具有指数复杂性，难以在多项式时间内求解，是一个NP-难问题。由于非线性0-1优化问题的变量是离散的，连续变量的最优性理论(KKT最优性条件等)不能直接应用。因此，如何将原来的0-1优化问题转化为连续的非线性优化问题是模型求解的关键。注意到约束(12)中xijkBlB∈{0,1},∀i,j,kB,lB∈N等价于:

xijkBlB≥0, 1-xijkBlB≥0,xijkBlB(1-xijkBlB)=0, ∀i,j,kB,lB∈N。

(13)

对任意∀i,j,kB,lB∈N，有xijkBlB2+(1-xijkBlB)2>0成立，即严格互补条件成立。于是，可利用NCP函数来刻画约束(13)，引入Fischer-Burmeister函数：

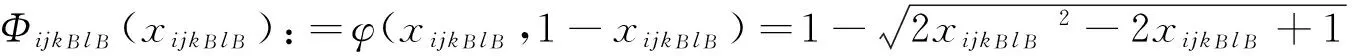
(14)

是处处可微的。对于约束(14)，有:

(15)

其中eijkBlB为n4×1向量，满足(eijkBlB)ijkBlB=1且有:

(eijkBlB)uvsBtB=0,∀u≠i,v≠j,sB≠kB,tB≠lB。进一步有：

(16)

(17)

相应的，对于约束(12)中ykB∈{0,1},∀kB∈N的转化与xijkBlB一致。模型(2)-(12)可转化为连续的非线性优化问题:

s.t.ΦijkBlB(xijkBlB)=0,ΦkB(ykB)=0,∀i,j,kB,lB∈N.

(18)

5.2 基于凝聚函数的松弛问题

对于模型(18)，采用乘子罚函数求解，需引入n4+n个Lagrange乘子，增加了乘子迭代难度。注意模型(18)可行域有F(模型18)={ΦijkBlB(xijkBlB)=0,ΦkB(ykB)=0,∀i,j,kB,lB∈N}，记:

ψ(xijkBlB,ykB)=(Φ1111(x1111),…,Φnnnn(xnnnn),Φ1(y1),…,Φn(yn)),

(19)

ψmax(xijkBlB,ykB)=max{(Φ1111(x1111),…,Φnnnn(xnnnn),Φ1(y1),…,Φn(yn))},

(20)

则有:

F(模型18)⟺{(xijkBlB,ykB):ψmax(xijkBlB,ykB)=0}

(21)

证明：对于∀xijkBlB,ykB∈[0,1]，若ψmax(xijkBlB,ykB)=0，则ΦijkBlB(xijkBlB)≤0,ΦkB(ykB)≤0，而ΦijkBlB(xijkBlB),ΦkB(ykB)值域有ΦijkBlB(xijkBlB)≥0,ΦkB(ykB)≥0，则ΦijkBlB(xijkBlB)=0,ΦkB(ykB)=0；反之亦然，证毕。

注意到ψmax(xijkBlB,ykB)在集合{(xijkBlB,ykB):ψμ(xijkBlB,ykB)=ψν(xijkBlB,ykB),μ,ν=1,2,…,(n4+n),μ≠ν}中处处不可微。为简化计算，利用凝聚函数:

(22)

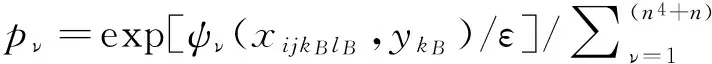
∑kB∈NFkBykB,

s.t.ψε(xijkBlB,ykB)=0.

(23)

引理1ψmax(xijkBlB,ykB)<ψε(xijkBlB,ykB)<ψmax(xijkBlB,ykB)+εln(n4+n).

证明：函数ψε(xijkBlB,ykB)可等价变形为:

ψε(xijkBlB,ykB)=ψmax(xijkBlB,ykB)+εln

ykB)]/ε}.

(24)

由于ψμ(xijkBlB,ykB)≤ψmax(xijkBlB,ykB)，则0≤exp{[ψμ(xijkBlB,ykB)-ψmax(xijkBlB,ykB)]/ε}≤1，且至少存在一个指标μ使得ψμ(xijkBlB,ykB)=ψmax(xijkBlB,ykB)，于是exp{[ψμ(xijkBlB,ykB)-ψmax(xijkBlB,ykB)]/ε}=1，从而:

0<ψε(xijkBlB,ykB)-ψmax(xijkBlB,ykB)≤εln(n4+n).

(25)

引理2随着ε→0，ψε(xijkBlB,ykB)→ψmax(xijkBlB,ykB).

证明：令ε→0，由引理1易得:

ψε(xijkBlB,ykB)→ψmax(xijkBlB,ykB)

(26)

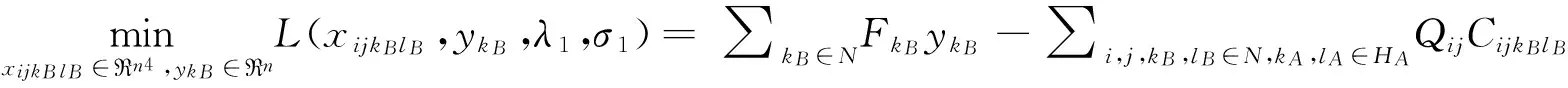
(27)

5.3 基于增广Lagrange函数的算法

(28)

于是，可取:

(29)

为下次迭代的Lagrange乘子。基于增广Lagrange乘子罚函数的算法[26]可写成

步3若‖ψε(Xκ+1)‖2≤‖ψε(Xκ)‖2/4，则转步4；σκ:=10σκ；转步2。

步4计算λκ+1；σκ+1:=σκ,κ:=κ+1，转步2。

6 算例仿真

6.1 数据选取

假设存在一个港口集合N={1,2,…,12}的海运市场，任一港口u的投资成本Fu、单位中转价格Cu/时间Tu列示于表1；任意两个港口u,v之间的单位运输价格Cuv/时间Tuv列示于表2；所有起讫港口之间的非弹性需求Qij(OD流量矩阵)列示于表3；任意两个港口u,v之间运输的服务质量Θuv列示于表4。计算时，枢纽港口之间单位运输价格的折扣因子α={0.2,0.4,0.6,0.8,1.0}，领导者A决定设计枢纽港口的数量pA={1,2,3,4}与对应的部分航线连接集合VA列示于表5，任一航线连接的吸引力模型的灵敏系数β=0.75和γ=1.71，权重系数θ={0,0.2,0.4,0.6,0.8,1.0}。对于模型求解的算法，ε=107(充分大常数)、X1=(0.5,0.5,…,0.5)、λ1=0.5、σ1=13000、δ=0.05和Κ=500，对不同情境下跟随者B基于服务约束的轴-辐式海运网络优化决策进行验证。

6.2 权重系数θ对跟随者B利润Z和市场份额M的影响

在pA=3固定及枢纽港口之间单位运输价格的折扣因子α={0.2,0.4,0.6,0.8,1.0}五种情景下，分析不同权重系数θ={0,0.2,0.4,0.6,0.8,1.0}对跟随者B利润Z和市场份额M的影响，其中M=∑i,j,kB,lB∈NPijkBlBQij/∑i,j∈NQij。由图1和图2可知，对于不同的α={0.2,0.4,0.6,0.8,1.0}，θ与Z存在一定的正相关性。随着θ增加，托运人对海运企业提供任一航线连接的单位服务价格Cijkl更加重视，跟随者B可通过建立多个枢纽港口来降低其单位服务价格Cijkblb以争取更多的市场机会。在θ=0托运人不考虑单位服务价格Cijkl时，Z和M统一收敛于8207495.73USD和33.67%，由于单位服务时间TijkBlB固定，跟随者B可寻的最佳方案为枢纽港口4,5,8的轴-辐式海运网络是唯一的。在θ=1.0托运人不考虑单位服务时间Tijkl时，Z和M均达到系列峰值，即使α=1.0不存在规模经济效应时，跟随者B也可通过建立合适的枢纽港口优化其提供的航线连接来争取一定的利润空间；对于α=0.2存在较大规模经济效应，跟随者B完全可通过建立大量的枢纽港口来吸引对单位服务价格Cijkl极其敏感的托运人，此时Z和M达到15907167.78USD和63.22%几乎两倍于θ=0时。可见θ>0托运人考虑单位服务价格Cijkl时，α对于Z和M有着重要影响，α越小，规模经济效应越明显时越有利于跟随者B进入海运市场。

表1 任一港口u的投资成本Fu和单位中转价格Cu/时间Tu(单位：USD, USD/TEU, 天)

表2 任意两个港口u,v之间的单位运输价格Cuv/时间Tuv(单位：USD/TEU, 天)

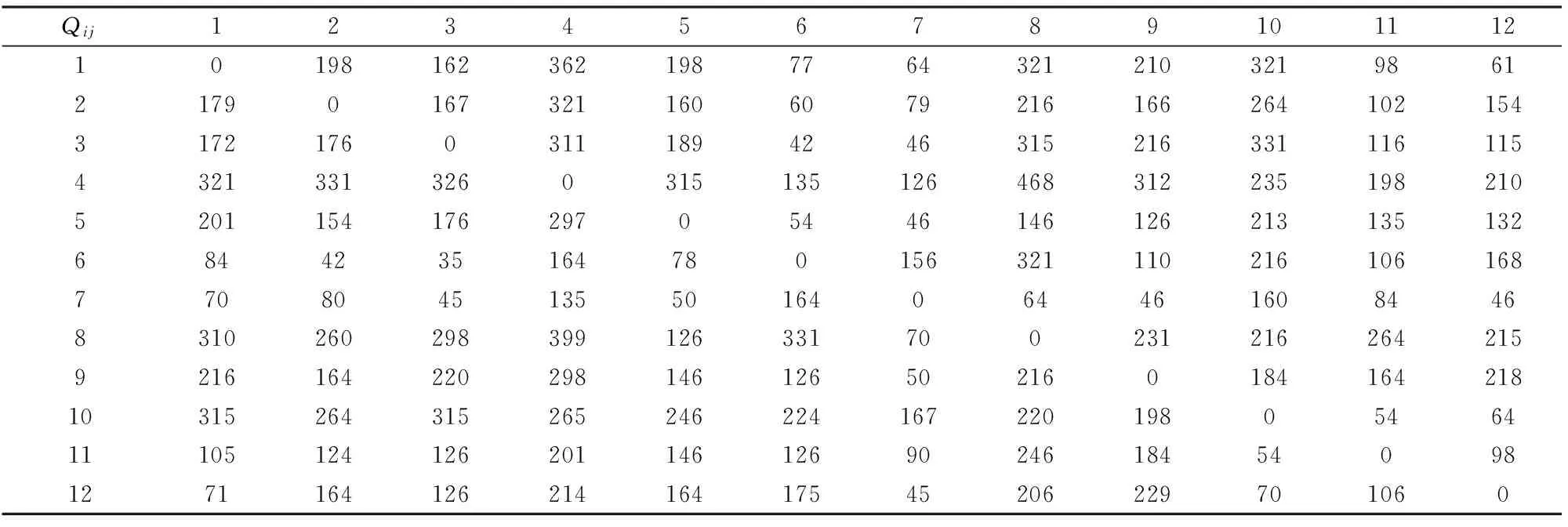
表3 所有起讫港口i,j之间的非弹性需求Qij(单位：TEU)

表4 任意两个港口v,v之间运输的服务质量Θuv

表5 领导者A决定设计枢纽港口的数量pA={1,2,3,4}与对应的部分航线连接集合VA

图1 不同权重系数θ对跟随者B利润Z的影响 图2 不同权重系数θ对跟随者B市场份额M的影响

图3 不同规模经济效应α对跟随者B利润Z的影响 图4 不同枢纽港口数量pA对跟随者B利润Z的影响

6.3 规模经济效应α对跟随者B利润Z的影响

在θ=0.4固定及领导者A的枢纽港口数量pA={1,2,3,4}四种情景下，分析不同枢纽港口之间单位运输价格的折扣因子α={0.2,0.4,0.6,0.8,1.0}对跟随者B利润Z的影响。θ=0.4表示托运人在选择海运企业提供任一航线连接时相比单位服务价格Cijkl稍偏好于单位服务时间Tijkl。由图3可知，α较小时Z明显高于α较大时的Z。在α=0.2存在较大规模经济效应时，跟随者B可通过建立多个枢纽港口来占据有利的竞争位势，与6.2的结论一致；在α=1.0不存在规模经济效应时，因跟随者B无法优化单位服务价格CijkBlB使其基于服务约束的轴-辐式海运网络优化效果受到限制，相应系列的Z对比α=0.2时降低了44.62%、43.13%、43.08%和34.93%，而这还是在θ=0.4情景下关于Z的对比，足以见证规模经济效应α对跟随者B利润Z的重要性。需注意的是，不论α大小，Z随着pA增加出现了不同程度的减少，这是因为pA>1时领导者A同样可享用规模经济效应α，将影响着跟随者B提供某些航线连接对托运人的吸引力。在α=1.0相当于单位服务价格Cijkl固定时，相应系列的Z为8753311.66USD、8514344.49USD、8242328.90USD和8094938.28USD较为接近但未统一收敛于某一定值，这是因为建立海运企业提供任一航线连接的吸引力模型Uijkl时采用的是比例模型而非二元离散选择模型。

6.4 枢纽港口数量pA对跟随者B利润Z的影响

在α=0.8固定及托运人对海运企业提供任一航线连接的吸引力模型的权重系数θ={0,0.2,0.4,0.6,0.8,1.0}五种情景下，分析领导者A不同枢纽港口数量pA={1,2,3,4}对跟随者B利润Z的影响。因α=0.8不存在较大规模经济效应，不同权重系数θ下Z的变化幅度不大。由图4可知，pA较大时Z明显小于pA较小时的Z，在pA=4领导者A在单位服务价格Cijkl和单位服务时间Tijkl为托运人可提供较具竞争力的航线连接时，相应系列的Z对比pA=1时降低了13.57%、9.59%、6.73%、11.97%、13.16%和11.13%，说明领导者A枢纽港口的增加可使其有效覆盖较大范围的海运需求来巩固其竞争位势，与6.3的结论一致。在θ=0托运人不考虑单位服务价格Cijkl时，可进一步反映领导者A与跟随者B之间的竞争关于pA的变化，对于港口集合N=12的海运市场pA>2时跟随者B的利润空间将受到较大挤压，但若θ>0.5托运人较多考虑单位服务价格Cijkl时，跟随者B仍可利用轴-辐式海运网络优化来争夺一定的利润。直观来看，不论pA大小，即使在α=0.8只存在较小规模经济效应时，Z随着θ增加显著提高，这也证实6.2的结论。

7 结语

本文针对同一海运市场中不同的海运企业——领导者与跟随者在设计多分配的轴-辐式海运网络时引起的竞争问题，突破已往枢纽港口集合是给定的假设，将航线连接设计扩展为可存在多条，考虑了服务质量价格时间三个因素对托运人的选择行为的影响，基于服务约束的吸引力模型，建立了竞争环境下一种新的基于服务约束的轴-辐式海运网络优化问题的数学模型，是一个连续型的枢纽选址模型。鉴于模型是一个非线性0-1优化问题，利用NCP函数中Fischer-Burmeister函数将原问题转化为连续的非线性优化问题，基于此，通过凝聚函数将问题进一步简化为只含有一个等式约束的连续的非线性优化问题，再利用增广Lagrange乘子罚函数法对其松弛问题进行求解。最后，通过算例仿真分析了不同情境下跟随者基于服务约束的轴-辐式海运网络优化问题，仿真结果显示：(1)跟随者在托运人不考虑单位服务价格时，受单位服务时间固定的影响其可寻的最佳方案是唯一的且不同规模经济效应下的利润统一收敛于某一定值，但在托运人考虑单位服务价格时，即使不存在规模经济效应时跟随者也可通过建立合适的枢纽港口来获取一定的市场机会。(2)跟随者在存在较大规模经济效应时其利润最可观，但在不存在规模经济效应相当于单位服务价格固定时，跟随者的利润因领导者决定设计枢纽港口的数量增加将出现大幅下滑但不会统一收敛于某一定值，这是因为基于服务约束的吸引力模型采用的是比例模型而非二元离散选择模型。(3)跟随者在领导者仅设计1个枢纽港口时可通过建立大量的枢纽港口来争夺丰厚的利润，但对于港口集合N={1,2,…,12}的海运市场，领导者只需设计枢纽港口的数量大于2，跟随者的利润空间便会受到较大挤压，这是因为领导者同样可享用规模经济效应为托运人提供具有竞争力的航线连接，即便是在托运人不考虑单位服务价格时。上述仿真结果可为跟随者基于服务约束进行合理的轴-辐式海运网络优化以争夺更多的利润和市场份额来参与海运竞争提供可验证的管理启示，但研究中考虑的竞争因素、网络因素和选择行为因素仍比较有限，比如多港挂靠的航线连接、航线连接的中转港口次数、枢纽港口的拥堵状况、托运人对服务的不同喜好等，因此考虑更多现实因素的竞争环境下的轴-辐式海运网络优化问题仍有待深化研究。

[1]HeldD,McGrewAG,GoldblattD,etal.Globaltransformations:Politics,economicsandculture[M].Basingstoke,UK:MacmillaninassociationwithPoliticalStudiesAssociation, 2000.

[2]AsgariN,FarahaniRZ,GohM.Networkdesignapproachforhubports-shippingcompaniescompetitionandcooperation[J].TransportationResearchPartA:PloicyandPractice, 2013, 48: 1-18.

[3]MunariPF.Competitioninlinershipping[M].BerlinHeldelbery:Springer, 2012.

[4] 王成金. 集装箱港口网络形成演化与发展机制[M]. 科学出版社, 2012.

[5]DucruetC,NotteboomT.Theworldwidemaritimenetworkofcontainershipping:Spatialstructureandregionaldynamics[J].Globalnetworks, 2012, 12(3): 395-423.

[6]ZhengJianfeng,MengQiang,SunZhuo.Linerhub-and-spokeshippingnetworkdesign[J].TransportationResearchPartE:LogisticsandTransportationReview, 2015, 75(3): 32-48.

[7] 李阳. 轴-辐式网络理论及应用研究[D]. 上海: 复旦大学, 2006.

[8]CampbellJF,O’KellyME.Twenty-fiveyearsofhublocationresearch[J].TransportationScience, 2012, 46(2): 153-169.

[9]AlumurS,KaraBY.Networkhublocationproblems:Thestateoftheart[J].EuropeanJournalofOperationalResearch, 2008, 190(1): 1-21.

[10]KlincewiczJG.Hublocationinbackbone/tributarynetworkdesign:Areview[J].LocationScience, 1998, 6(1): 307-335.

[11]FaharaniRZ,HetmakfarM,ArabaniAB,etal.Hublocationproblems:Areviewofmodels,classification,solutiontechniques,andapplications[J].ComputersandIndustrialEngineering, 2013, 64(4): 1096-1109.

[12]MarianovV,SerraD,ReVelleC.Locationofhubsinacompetitiveenvironment[J].EuropeanJournalofOperationalResearch, 1999, 114(2): 363-371.

[13]GelarehS,NickelS,PisingerD.Linershippinghubnetworkdesigninacompetitiveenvironment[J].TransportationResearchPartE:LogisticsandTransportationReview, 2010, 46(6): 991-1004.

[14] 赵宇哲. 竞争环境下的轴-辐式集装箱海运网络设计问题[J]. 中国管理科学, 2015, 23(7):103-112.

[15] 陈康, 郭利泉, 杨忠振. 基于混合航线结构的集装箱航线与空重箱运输综合优化模型[J]. 系统工程理论与实践, 2014, 34(1):122-128.

[16]ZhengJianfeng,MengQiang,SunZhuo.Impactanalysisofmaritimecabotagelegislationsonlinerhub-and-spokeshippingnetworkdesign[J].EuropeanJournalofOperationalResearch, 2014, 234(3): 874-884.

[17] 赵宇哲, 段浩, 张连如. 不确定OD需求下的轴-辐式集装箱海运网络设计[J]. 系统工程, 2014, 32(4):21-29.

[18]ReillyWJ.Thelawofretailgravitation[M].NewYork:KnickerbockerPress,1931.

[19]HuffDL.Definingandestimatingatradingarea[J].JournalofMarketing1964, 28(3):34-38.

[20]EiseltHA,MarianovV.Aconditionalp-hublocationproblemwithattractionfunctions[J].ComputersandOperationsResearch, 2009, 36(12): 3128-3135.

[21]OrtúzarJD,WillumsenLG.Modellingtransport[M].WestSussex,UK:Wiley-Blackwell, 2011.

[22] 李进, 傅培华, 李修琳,等. 低碳环境下的车辆路径问题及禁忌搜索算法研究[J]. 中国管理科学, 2015, 23(10):98-106.

[23] 方健, 徐丽群. 随机需求下考虑碳排放的供应商选择问题研究[J]. 中国管理科学, 2016, 24(2): 56-60.

[24]LiXSingsi.Anaggregateconstraintmethodfornon-linearprogramming[J].JournaloftheOperationalResearchSociety, 1991, 42(11):67-110.

[25] 杨庆之. 对凝聚函数法的分析[J]. 计算数学, 1996, 11(4):405-410.

[26] 袁亚湘. 非线性优化计算方法[M]. 北京: 科学出版社, 2008.

The Hub-and-spoke Shipping Network Optimization with Service Constraints in a Competitive Environment

ZHAO Yu-zhe1, 2, ZHOU Jing-miao2, KUANG Hai-bo1

(1.Collaborative Innovation Center for Transport Stndies, Dalian Maritime University, Dalian 116026, China;2.Faculty of Management and Economics, Dalian University of Technology, Dalian 116023, China)

The current trend of global trade enhance the importance of shipping service, since it is in charge of transporting up to 90% of the trade volume. Recently, a number of shipping alliances have emerged to dominate the shipping market, and most of the smaller shipping companies are suffering from an ongoing loss of their profits. It is therefore essential for the smaller shipping companies-that are not operating in shipping alliances to seek for ways of competing with the shipping alliances in order to achieve some higher profits or at least to recover the lost market shares. An integer nonlinear programming model is propesed for the hub-and-spoke shipping network optimization with service constraints in a competitive environment to address the considered problem. An existing shipping alliance, called the leader, utilizes a transportation network with a multi-allocation hub-and-spoke topology. A new shipping company, the follower, wants to offer its shipping service in the same shipping market, using its own multi-allocation hub-and-spoke shipping network and setting service quality, service time and service cost so as to maximize its profits. The question to be answered is: Can the follower obtain profits under these conditions, even with same service quality, service time and service cost ofthe leader? In order to answer this question, our procedure finds how many hub ports to locate, where should they be located, what is the best route network. The contributions of this paper are as follows. In the first place, continuous hub location model (the domain of hub ports is a plane not a series of particular ports) is formulated. Secondly, the numbers of routes existing in the origin-destination ports are extended. Third, an attraction function which is a proportional model not a discrete choice model is provided to simulate the consignors’ choice behavior. Finally, the integer nonlinear problem is solved using an augmented Lagrange function method based on NCP function and coagulation function. Consequently, the conclusions are achieved by example simulation that, (1) the follower will obtain certain profits by opening moderate number of hub ports in the case of service cost is considered by consignors (θ>0), even if there is no economies of scale (α=1.0); (2) the follower's benefits will be the most significant if there are high economies of scale (α=0.2), but its profits in the case of the leader has different amount of hub ports (PA) located will not unified converges to a certain value if there is no economies of scale (α=1.0) by the fact of a proportional model is applied; (3) the follower can obtain much profits by opening more hub ports if the leader has one hub ports (PA=1), but its capability of obtaining a higher profits will be reducing if the leader has operated more than two hub ports (PA>2) for the 12-node versionof the shipping network.

hub-and-spoke network; competition; service constraints; continuous approaches; augmented Lagrange function method

1003-207(2016)11-0047-11

10.16381/j.cnki.issn1003-207x.2016.11.006

2015-05-20；

2015-10-22

国家自然科学基金资助项目(71403035, 71273037); 教育部“创新团队发展计划”项目(IRT13048); 辽宁省自然科学基金(2015020080); 中国博士后科学基金面上资助项目(2016MS90227)；辽宁省经济社会发展课题重点资助项目(2017lslktzd-004);辽宁省高等教育有内涵发展专项资金资助项目(20110116103)

赵宇哲(1983-), 男(汉族), 黑龙江大庆人, 大连海事大学交通运输管理学院, 副教授, 博士, 研究方向: 海运网络优化、 港口绿色增长,Email:zhaoyuzhe@126.com.

U6-9;O

A