突变地质界面盾构隧道开挖面极限支护压力研究
2016-04-10王国富孙捷城路林海王渭明
王国富,孙捷城,路林海,王渭明,王 丹
(1.山东科技大学 土木工程与建筑学院,山东 青岛 266590;2.济南轨道交通集团有限公司,山东 济南 250101)
随着城镇区域化进程和城市轨道交通的快速发展,越来越多的地铁盾构隧道不可避免地穿越岩—土—水复杂地质环境。该环境中岩—土介质不均匀土压力、多相介质界面效应、地下水渗流作用等特点成为了困扰施工安全的关键难题。尤其在岩—土—水突变地质界面中,围岩由岩质突变为富水软黏土或砂土,刚度显著减小,同时孔隙水压力剧增,若不及时调整盾构隧道开挖面支护压力,极易造成刀盘前方土压失衡,诱发开挖面涌水突泥、盾构姿态偏移、地层大变形等工程灾害[1-5]。因此,研究突变地质界面下盾构隧道开挖面支护压力的变化特征和围岩失稳模式,对开挖面稳定性控制与灾害预防设计具有重要的理论与实践意义。
目前,关于开挖面支护压力的研究主要集中在单一地质体[6-10]或水平成层地质条件[11-13],而对竖向突变地质界面的盾构开挖面稳定性研究还鲜见报道。因此,本文基于筒仓理论,建立适用于突变地质界面的梯形棱柱体极限平衡模型,推导开挖面支护压力计算公式;以济南轨道交通R1线隧道下穿腊山河为工程背景,进行实例计算分析,并结合数值模拟,研究开挖面距突变地质界面不同距离(简称界面距离)时的开挖面破坏模式和围岩变形分布特征,揭示极限支护应力与界面距离的演化规律,并探讨地质界面前后的黏聚力、内摩擦角和界面倾角等因素对开挖面稳定性的影响。
1 开挖面极限支护压力分析
1.1 建立梯形棱柱体极限平衡模型
在盾构隧道开挖面稳定性分析模型中,目前应用最广泛的是基于筒仓理论的楔形棱柱体模型[7]。然而,在突变地质界面附近,受强弱地质体力学性质差异的影响,将产生沿界面滑移的破坏,隧道开挖面稳定性分析模型由楔形体模型转化为梯形体模型,为此提出梯形棱柱体极限平衡模型,其模型简图及极限受力情况如图1所示。
图1(a)中:AOFE-BCF′E′为梯形滑动体;OABC为隧道的等效开挖面;EE′M′M为地质界面;IJJ′I′为地下水位;MKK′M′为地表面;β为梯形体的滑动破裂角。
图1(b)中:P为盾构刀盘作用于开挖面的总支护压力;F为棱柱体作用于梯形体上的力;G为梯形体自重;T1,T2,T3分别为对应面上的总剪力;N1,N3分别为作用于对应面上的总压力;L为棱柱体边长;D为隧道直径。

图1 梯形棱柱体极限平衡模型
在建立梯形棱柱体极限平衡模型及分析过程中,进行如下假设。
(1) 土体在地质界面前、后是均质,且各向同性、刚塑性材料,服从Mohr-Coulomb破坏准则,滑裂面的抗剪强度τ的计算公式为
τ=c+σtanφ
(1)
式中:c为土体黏聚力;σ为剪切面上的正应力;φ为土体内摩擦角。
(2) 在穿越地质界面过程中,开挖面破坏范围由梯形体和棱柱体组成,模型后侧边界总是为沿强弱地质界面的滑移面,即棱柱体边长随盾构掘进而逐步减小,其边长L为变量。
(3) 梯形体与开挖面的接触面为正方形,其边长等于隧道直径D。
(4) 梯形体倾斜面及竖直面上的竖向应力随深度呈线性递增分布。
1.2 开挖面极限支护压力计算公式推导
根据图1(b)所示的梯形体平面受力图,当开挖面前方土体处于极限平衡状态时,建立梯形体水平与竖直方向的受力平衡方程为
P+T1sinβ+2T2sinβ=N1cosβ+N3
(2)
F+G=T1cosβ+2T2cosβ+N1sinβ+T3
(3)
由式(3)得
(4)
将式(4)代入式(2)并整理得
(5)
式中各参数计算过程如下。
1) 梯形体自重G
(6)
式中:γ为土体饱和重度;SAOFE为AOFE平面的面积。
2) 棱柱体作用于梯形体上的力F
F=σvSOCF′F=σvDL
(7)
式中:σv为棱柱体作用于梯形体的竖向应力;SOCF′F为OCF′F平面的面积。
根据太沙基松动土压力理论[14],并将其扩展到含有地质界面的三维条件下。假设形成的柱体松动区的长度为L,宽度为D,在埋深为z处土体微元的受力模型如图2所示。图2中:q为地面超载;w为土体微元自重;σh和τ′分别为土体微元侧面的正应力与剪应力。
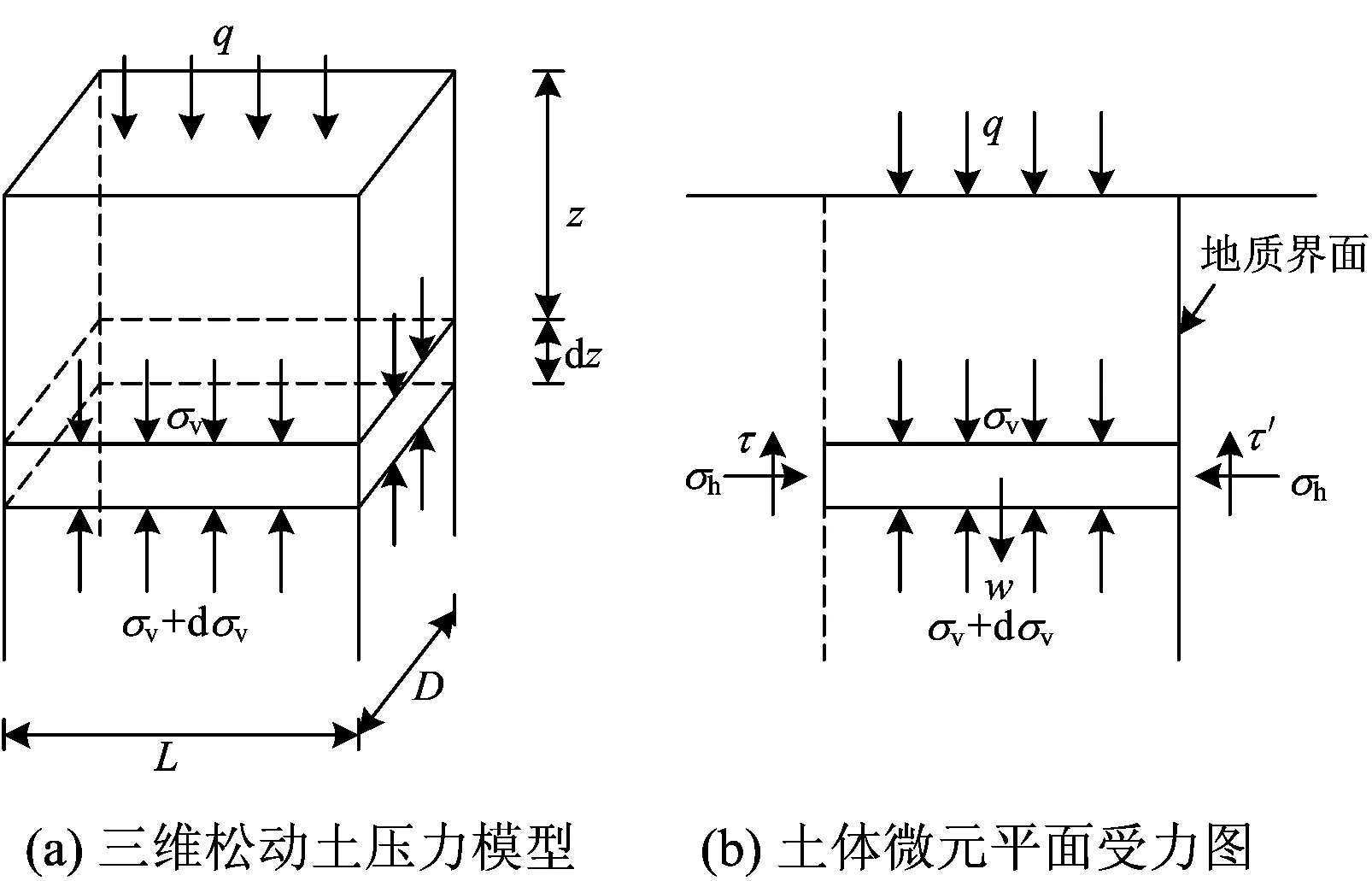
图2 松动土压力计算模型
由图2可知,松动土体微元的竖向受力平衡方程为
σvS+γSdz=(σv+dσv)S+Dτdz+2Lτdz+Dτ′dz
(8)
式中:S为微元体的上表面积,S=DL。
又因为
τ=c+σhtanφ=c+λlσvtanφ
τ′=c′+σhtanφ′=c′+λlσvtanφ′
式中:c′和φ′分别为界面后土体的黏聚力和内摩擦角,λl为棱柱体的侧压力系数。
则式(8)可改写为

(9)
解式(9)一阶非齐次常系数微分方程得
(10)
其中,
式中:A0为待定常数。
(11)
将式(11)代入式(10)得
(12)
当存在地下水且不考虑渗流作用时,开挖面仅受到静水压力的作用,则式(12)应改写为

qe-P0H
(13)
其中,

3) 梯形体倾斜面ABE′E上的剪力T1
根据文献[7]和假设(4),梯形体倾斜面ABE′E上的总剪力为
菌核病是油菜生长过程中最为常见的一种病虫害,菌核病主要是在油菜生长初期发病,一般高发于油菜开花期,秋播油菜由于受到气温等自然因素的影响,菌核病的发病期一般会有不同程度的延长。油菜感染菌核病的主要表现为植物叶片的边缘明显发黄,中间会生长出不规则的黄褐色圆斑,受菌核病感染越重,圆斑颜色越深,会逐渐变成灰褐色斑点,还会导致油菜茎表皮破裂,如不加以防治,会导致油菜发黄枯死。

(14)

将式(4)代入式(14)解得

(15)
4) 梯形体竖直面AOFE与BCF′E′上的剪力T2
根据假设(4)竖向应力随深度的增加呈线性递增,则剪力T2的计算简图如图3所示。
由图3可知,滑动面AOFE(BCF′E′)上某一深度的竖向应力为
(16)

图3 剪力T2计算简图
则作用于AOFE微元面上的剪力为
dT2=[c+λσv(z)tanφ]ds
(17)
对式(17)进行积分得总剪力为
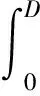

(18)
将式(16)代入式(18)进行积分计算并整理得
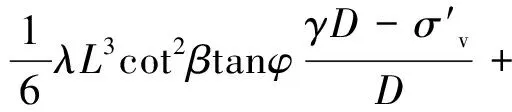
(19)
5) 梯形体竖直面EE′F′F上的剪力T3、压力N3
竖直面EE′F′F上的应力分布及其计算过程与剪力T2类似,则可推导得

(20)
对于压力N3,由于界面后主要为细砂土等非黏性土,采用水土分算可得

(21)
将式(6)、式(7)、式(13)、式(15)、式(19)—式(21)代入式(5),可得突变地质界面下盾构隧道开挖面极限支护压力P的计算式为

(22)
该梯形棱柱体模型适用于开挖面接近地质界面时,即0≤L≤Dtanβ,当盾构隧道开挖面距地质界面较远或已经穿越地质界面时,可以采用常规的楔形体模型计算。
对于某一特定工程,盾构尺寸及土体参数均为不变量,则由式(22)可知,极限支护压力P仅与破裂角β和梯形体长度L这2个变量有关,可表示为
(23)
2 工程实例计算分析
为验证本文提出的穿越突变地质界面时盾构隧道开挖面极限支护压力计算方法的可靠性,以济南轨道交通R1线盾构隧道下穿腊山河段岩—土—水多相介质环境为工程背景进行计算分析。
2.1 工程概况
济南轨道交通R1线王府庄站—大杨庄站区间隧道在K21+811.0至K21+892.0处下穿腊山河,腊山河宽60 m,水深约5 m,河底距隧道顶端约9.4 m。在距离河堤前约40 m处有1条明显的岩石与土体交界的地质界面,界面倾角为60°~85°,穿越段地质界面如图4所示,盾构机由岩石介质掘进至土体介质,Hw和H分别为隧道顶部到地下水位和地表的距离。界面前地质主要为中风化灰岩岩质,岩石强度较高,密度大,透水性弱;界面后地貌形态为厚冲积平原,地层主要为杂填土、黄土、粉质黏土、细砂土、黏土、胶结砂和卵石等[15]。各地层分布及物理力学参数见表1。
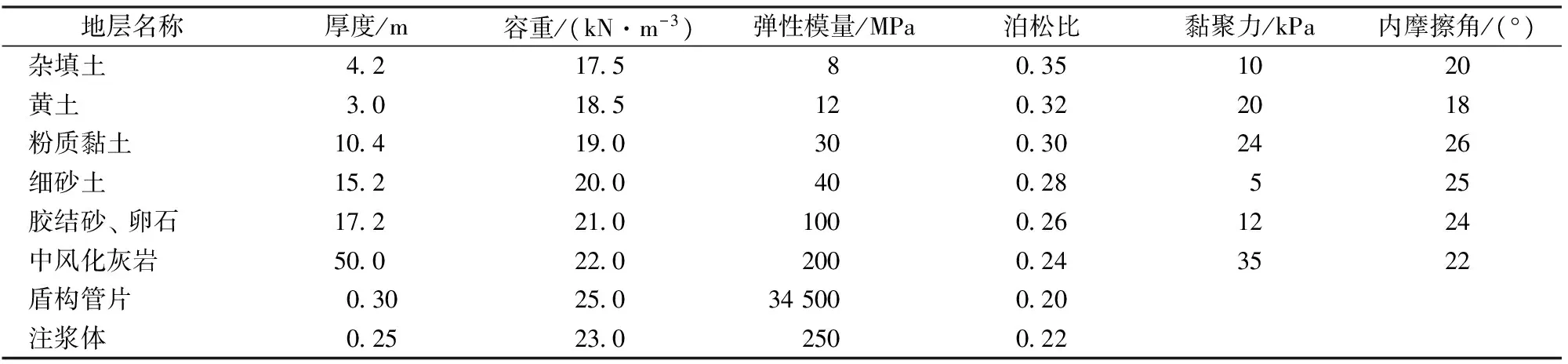
表1 地层及支护体物理力学参数
隧道开挖采用土压平衡盾构机,总长l=9.4 m,开挖直径为6.67 m,管片为钢筋混凝土结构,环宽1.2 m,外径D0=6.4m,内径D1=5.8 m。

图4 盾构穿越地质界面简化模型
2.2 计算结果分析
盾构隧道开挖面极限支护应力为
(24)
依据该工程地质体的力学参数,编制计算机程序计算不同破裂角β和梯形体长度L下的开挖面极限支护应力。
1) 滑块破裂角β的影响
破裂角β与梯形体长度L具有一定相关关系,为了便于分析不同L下β的变化情况,定义梯形体长度比k为
(25)
分别绘制梯形体长度比k=0.2,0.4,0.6,0.8,1.0下σp-β的关系曲线如图5所示。由图5可以看出:极限支护应力随k值的减小而不断增大,且变化趋势更加平缓,当k=1时,即L=Dtanβ,极限分析模型为常规的楔形棱柱体,其变化趋势与文献[16—18]模型试验所得结果较吻合,从侧面验证了本文推导的梯形体模型的可靠性;不同k值下极限支护应力与破裂角关系具有相似的变化规律,随着破裂角的增大,开挖面极限支护应力先增大后减小,约在β=34°时支护应力达到峰值,即为极限支护应力σp所对应的破裂角,该角度与秦建设[9]对滑块倾角的假设β=45°-φ/2相一致。
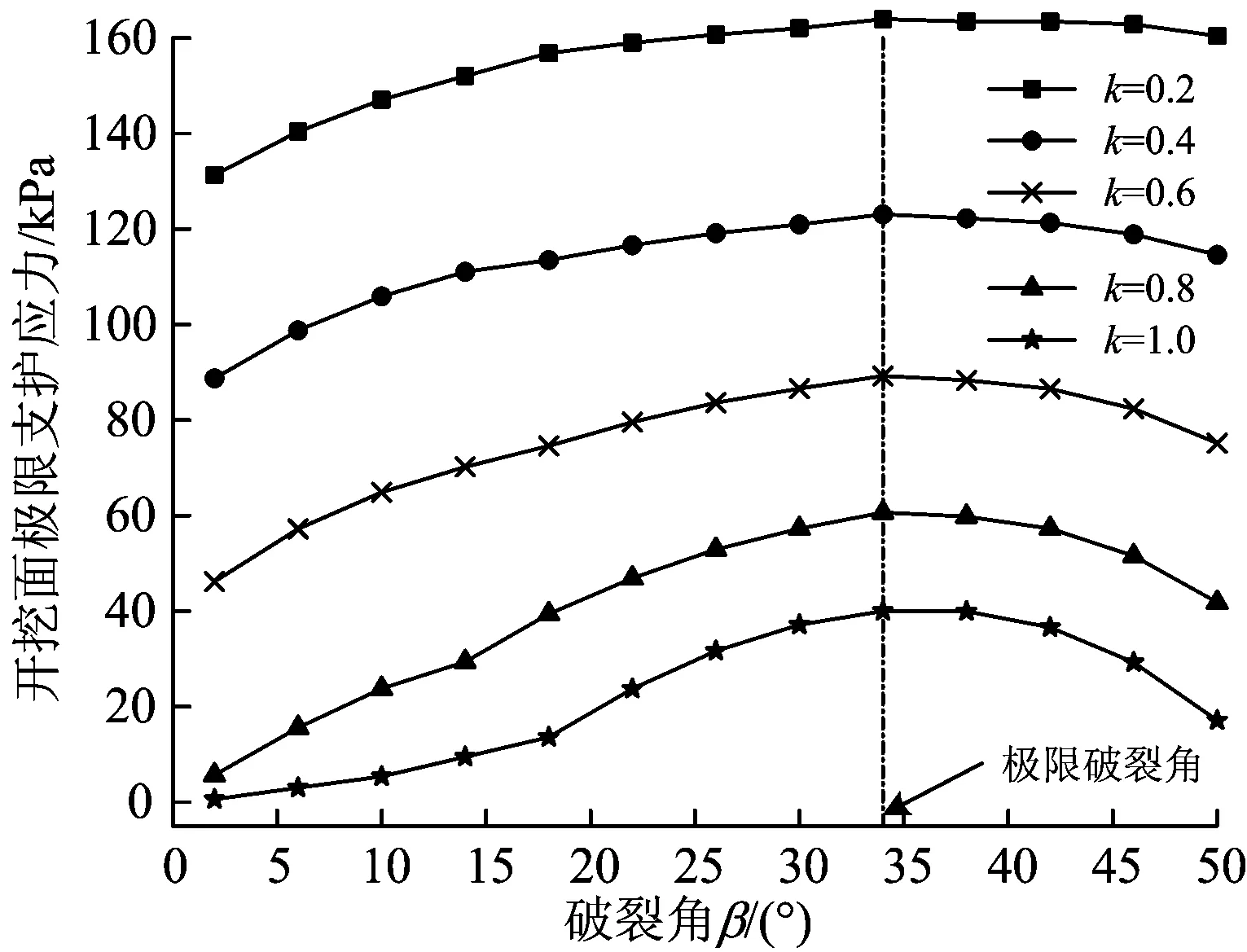
图5不同梯形体长度比时极限支护应力与破裂角的关系曲线
(2) 梯形体长度L的影响
图6为β=34°时L与σp的关系曲线。由图6可以看出:开挖面极限支护应力随着梯形体长度L的减小而逐渐增大,说明盾构由岩质进入土体过程中,开挖面越接近地质界面,维持开挖面稳定的极限支护应力越大,通过数据拟合得到其表达式为
σp=3.9L2-60.86L+226.73
0≤L≤Dtanβ
(26)

图6 极限支护应力与梯形体长度的关系曲线
3) 地质界面前后的极限支护应力分布
为了便于描述开挖面极限支护应力与界面距离的关系,进行无量纲归一化处理,引入界面距离比和支护应力比[8]的概念,计算公式分别为
(27)
(28)
式中:ε为界面距离比;δ为支护应力比;x为盾构掘进至某一位置时开挖面与地质界面的距离,σ0为隧道中心处的静止土压力。
结合本工程参数,计算得到界面附近不同界面距离比时的极限支护应力比,如图7所示,图中ε<0表示盾构开挖面尚未到达地质界面,ε>0表示盾构开挖面已经穿越地质界面。
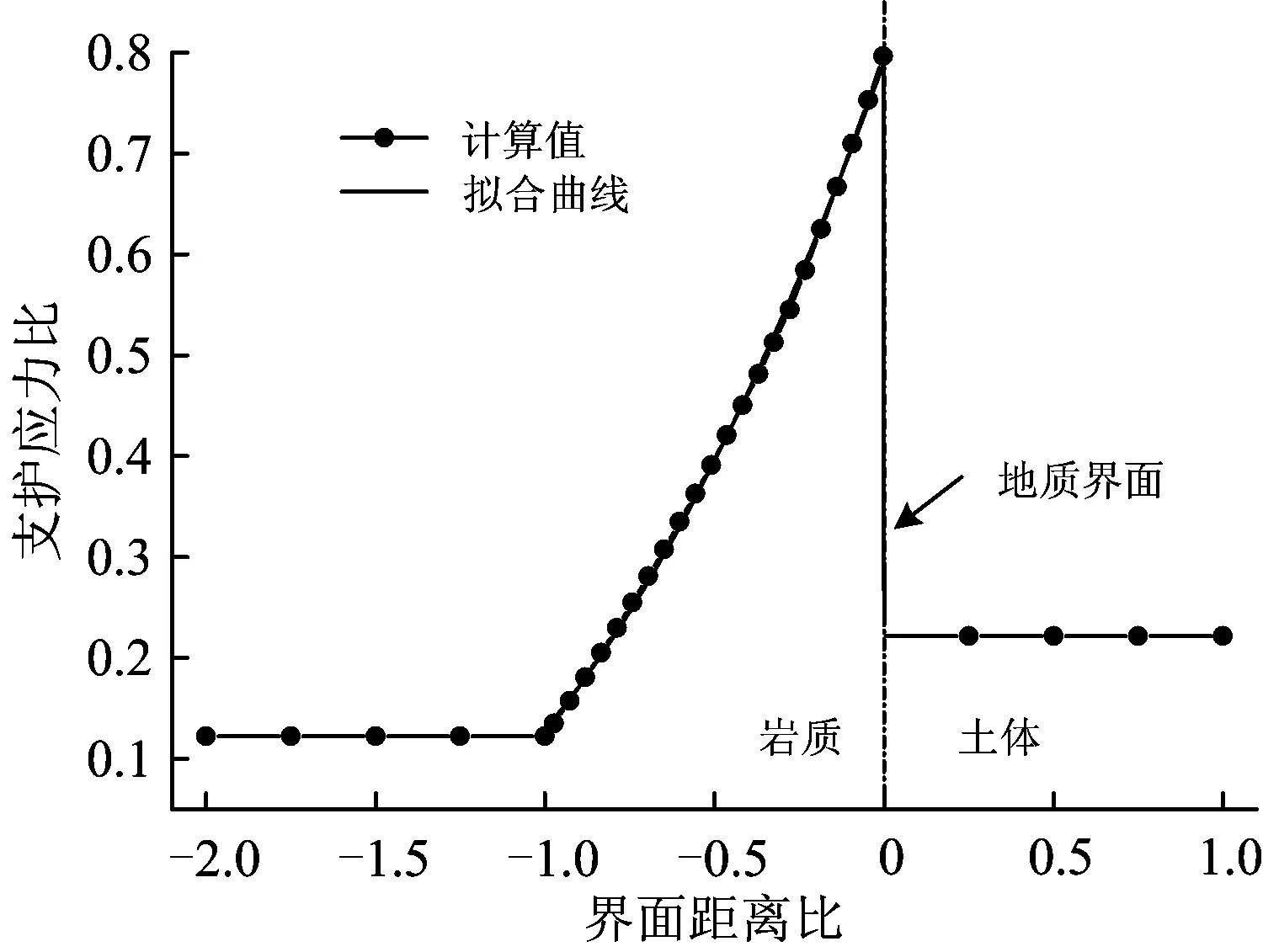
图7 地质界面前后的极限支护应力比分布
由图7可得如下结论。
(1)当界面距离比ε<-1时,盾构完全处于岩石介质中,其开挖面稳定尚未受到地质界面的影响,按照适用于均质地层的楔形棱柱体模型[7]进行计算,得到在岩质中的开挖面极限支护应力比为0.12。
(2)当-1≤ε≤0时,开挖面破坏模式由楔形体转化为梯形体,极限支护应力比开始逐步增大,其拟合公式为
δ=0.25ε2+0.92ε+0.79-1≤ε≤0
(29)
特别在ε=0(开挖面到达地质界面)时,极限支护应力达到峰值,其支护应力比为0.79,因此在该阶段应严格控制开挖面支护压力,避免发生涌水突泥事故。
(3)当ε>0(开挖面穿过地质界面)后,开挖面极限支护应力回到稳定状态,其开挖面破坏模式转化为常规的楔形棱柱体模型,计算得到在砂土中的极限支护应力比为0.22。
3 穿越突变地质界面时盾构隧道开挖面稳定性的数值分析
3.1 计算模型建立
采用FLAC进行数值模拟。模型的长×宽×高为60 m×60 m×50 m,上边界为自由面,四周受水平约束,底面为竖向约束。隧道围岩采用Mohr-Coulomb准则,管片衬砌采用实体弹性模型,盾尾注浆通过提高其加固区围岩参数来模拟。计算模型如图8所示,地层及支护体的物理力学参数见表1所示。

图8 计算模型
3.2 计算结果分析
结合图7的界面距离比影响范围,分别对开挖面距离地质界面的距离为6.4(x=D),4.3(x=Dtanβ),2,1,0 m和穿越界面后2 m共6种工况进行分析。
1) 开挖面破坏模式分析
当支护应力为40 kPa时开挖面围岩的变形等值线图如图9所示。由图9可知:随着开挖面距离地质界面越来越近,开挖面前方的围岩变形逐渐增大;当距离地质界面6.4 m时,基本不受界面效应的影响,围岩最大变形量为10.1 mm;当距离地质界面4.3 m时,受岩—土界面效应的影响使围岩变形增大,最大变形达14.7 mm,增幅为45.5%;当距离地质界面2 m时,围岩发生剧烈变形,开挖面破坏模式受界面作用转化为梯形体,变形范围主要集中于前方梯形区域;当开挖至地质界面时,破坏模式转变为典型的楔形体,最大变形已超过750 mm,开挖面已发生失稳破坏,说明在接近地质界面时,支护应力40 kPa远不能确保开挖面稳定。

图9 不同界面距离下的开挖面破坏模式
2) 围岩位移分布特征
为进一步分析地质界面附近围岩变形情况,布置测点如图10所示,计算得到各测点的围岩位移分布如图11所示。
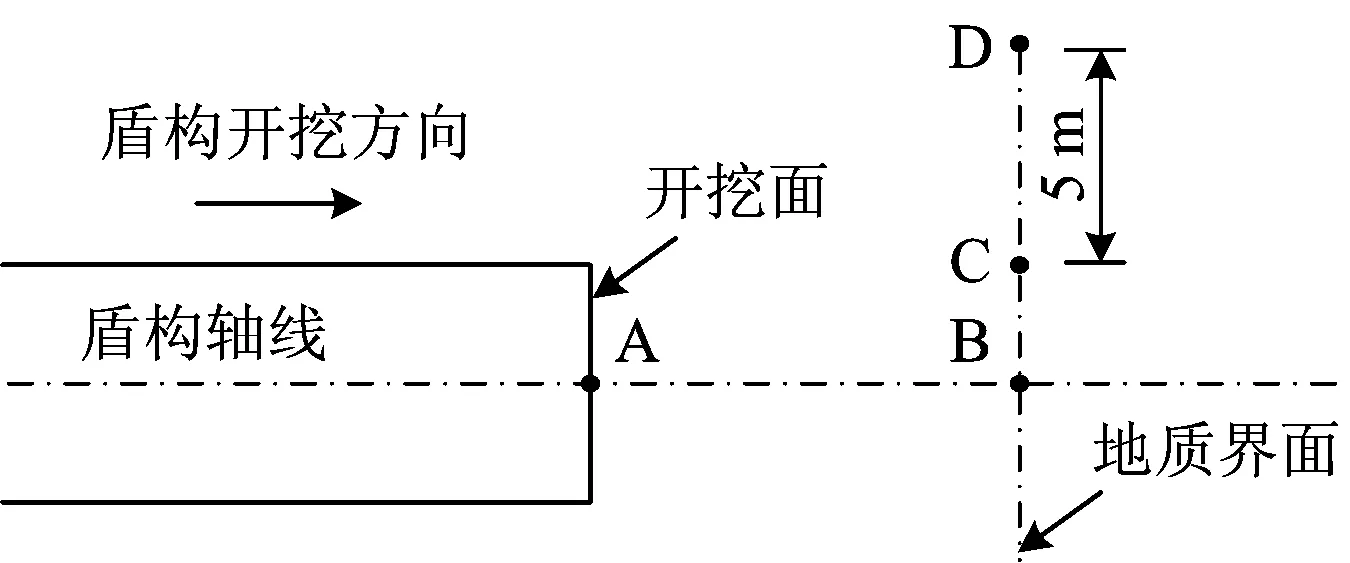
图10 地质界面周围测点布置
由图11可知:A和B测点的变形均随开挖面距离地质界面的减小而逐渐增大,当与地质界面的距离小于2 m时,变形量急剧增大,在接近地质界面时,变形量超过100 mm,开挖面发生失稳破坏;C和D测点的沉降值随界面距离的减小而增大,穿越地质界面后,沉降基本保持平稳,说明开挖面失稳破坏影响区域主要为前方范围,对拱顶上方影响相对较小。
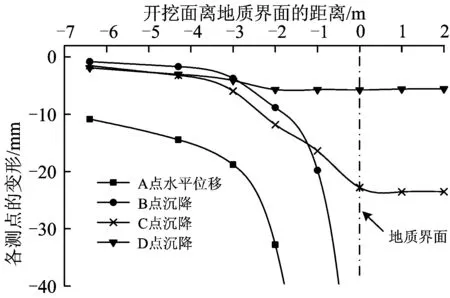
图11 各测点处围岩变形分布
3) 开挖面极限支护应力的变化
图12为开挖面支护应力比与A点水平位移的关系曲线。由图12可以看出:不同界面距离时A点水平位移均随支护应力比的减小而增大,且各曲线初始段(0.5≤δ≤1)的斜率随距界面距离的减小而逐渐增大,说明越靠近地质界面,受界面效应的影响越显著,隧道围岩的扰动敏感性越强,开挖面稳定性越不易控制。
4) 解析解与数值解对比分析
取图12中曲线斜率突然增大位置所对应的支护应力比为极限支护应力比,绘制不同界面距离下的极限支护应力比曲线,并与本文方法得到的解析解进行对比,如图13所示。由图13可以看出:解析解与数值解曲线的变化趋势基本吻合,验证了本文计算模型的可靠性;在接近地质界面时,数值解略小于解析解,这是由于本文采用梯形棱柱体模型计算时,仅将界面后土体简化为砂土进行参数加权平均处理,而数值模拟中地质界面后土体为多层土组成,等效黏聚力和内摩擦角有一定偏差;随开挖面与地质界面距离的减小,极限支护压力的解析解与数值解均呈现显著增大的趋势,两曲线拟合公式具有相同的形式,极限支护应力比是关于界面距离比的二次函数。
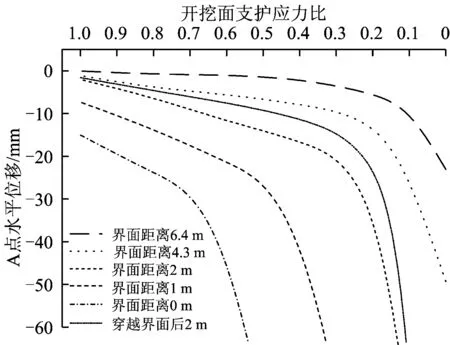
图12 开挖面支护应力比与A测点水平位移的关系
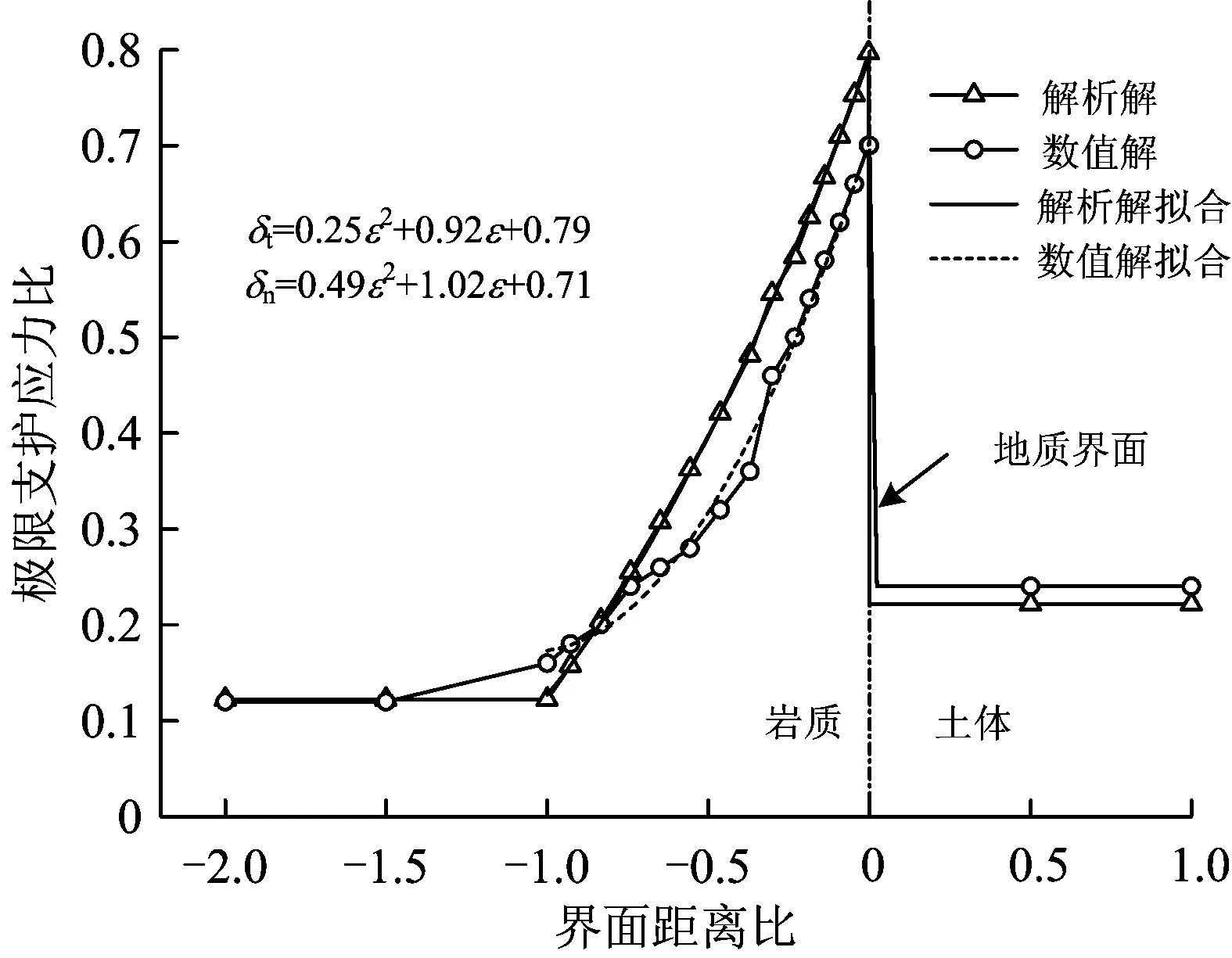
图13 极限支护应力比与界面距离的关系
综上所述,突变地质界面对开挖面稳定性具有显著影响,在靠近地质界面时,极限支护应力显著增大,在实际施工中,应充分重视开挖面前方地质勘查,及时调整盾构支护压力,以确保开挖面安全、稳定。
4 突变地质界面影响因素分析
地质界面两侧介质的黏聚力、内摩擦角及界面倾角等因素对开挖面的力学行为具有重要影响,采用本文的计算方法对上述因素进行敏感性分析。
4.1 黏聚力与内摩擦角的影响
为分析地质界面两侧土体参数的影响,定义地质界面前后的黏聚力比与内摩擦角比分别为c和f,设定岩质参数不变,逐步改变土质参数,得到不同c和f值下的开挖面极限支护应力曲线,如图14和图15所示。
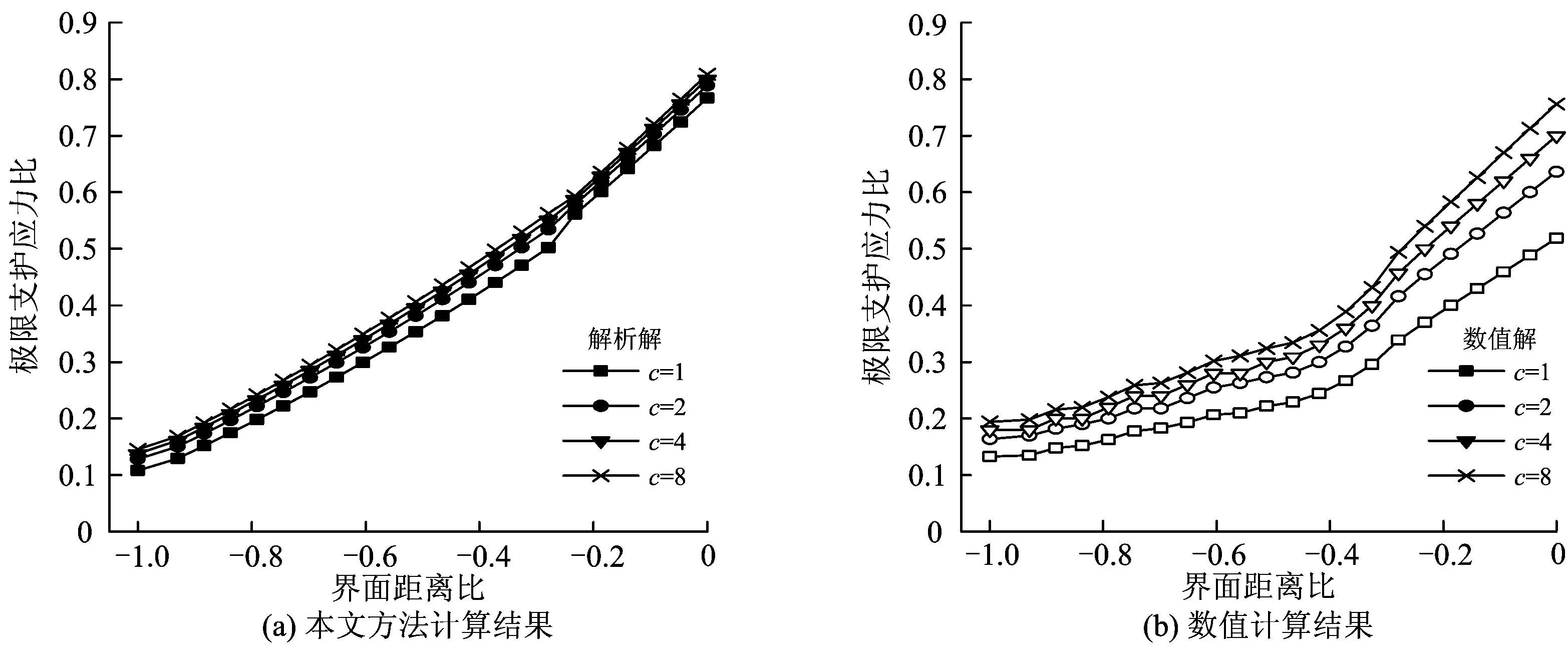
图14 两介质黏聚力比对极限支护应力比的影响曲线
由图14可知:随着地质界面前后黏聚力比的增大,开挖面的极限支护压力也逐渐增大,但增长幅度不明显;本文的理论计算结果与数值模拟结果基本一致,验证了梯形棱柱体模型的可靠性,临近地质界面时模拟值略小于理论值,这是由于理论计算时将地质界面后土层进行了平均化处理,致使开挖面变形略小。
由图15可知:开挖面极限支护压力随地质界面前后内摩擦角比的增大而增大,当f<1时,极限支护应力比的变化幅度相对较大,且随着开挖面与界面距离的减小,极限支护压力逐渐趋于平稳;当f≥1时,内摩擦角因素对开挖面稳定性的影响相对较小,且极限支护应力比的增长幅度随f值的增大越来越小。
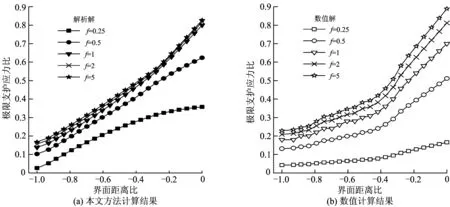
图15 两介质内摩擦角比对极限支护应力比的影响曲线
4.2 界面倾角的影响
绘制岩—土界面倾角θ为0°,±15°,±30°(0°为界面竖直,逆时针为正,顺时针为负)5种工况下开挖面极限支护压力与界面倾角的关系曲线,如图16所示。

图16 界面倾角对极限支护应力比的影响曲线
由图16可知:无论界面倾角正向增大(界面倾向于岩质)还是负向增大(界面倾向于土质),开挖面极限支护压力均逐渐增大,说明界面倾斜时对围岩稳定性的影响比界面垂直时更加显著;同一界面距离下,开挖面极限支护压力的大小顺序为30°>-30°>15°>-15°>0°,说明同一界面倾角下,倾向于岩质时所需的开挖面支护压力要大于倾向于土质时,即界面倾向于强体介质时开挖面更容易发生失稳破坏。
综上所述,岩—土界面对开挖面稳定性的影响随着界面前后地质体黏聚力、内摩擦角差异的增大和界面倾角的增大而显著增大。
5 结 论
(1) 在突变地质界面附近盾构隧道开挖面的稳定性与单一介质中显著不同,受地质体之间黏聚力、内摩擦角、抗剪强度等力学性质差异的影响,将产生沿弱体界面的滑移失稳,研究其开挖面破坏模式及围岩变形特性对施工安全与灾害预防具有重要意义。
(2) 基于筒仓理论,采用极限平衡分析法建立了突变地质界面下的梯形棱柱体计算模型,推导了开挖面极限支护应力计算公式,并进行了实例分析和模拟验证,对比结果表明本文提出的计算模型是合理的、可靠的。
(3) 计算结果表明,不同梯形体长度比下的极限破裂角大小相同,近似为45°-φ/2;开挖面极限支护压力随界面距离的减小而逐渐增大,当界面距离比ε为-1≤ε≤0时,开挖面的破坏模式由楔形体转化为梯形体,极限支护应力比是关于界面距离比的二次函数。
(4) 开挖面极限支护压力随着界面前后地质体黏聚力、内摩擦角差异的增大而增大,其中黏聚力比c以及内摩擦角比f≥1时对极限支护应力比δ的影响相对较小,当内摩擦角比f<1时对δ的影响相对较大。地质界面倾斜时对围岩稳定性的影响比其垂直时更加显著,且同一界面倾角下,界面倾向于强体介质时开挖面更容易发生失稳破坏。
[1]李术才,周宗青,李利平,等. 岩溶隧道突水风险评价理论与方法及工程应用[J]. 岩石力学与工程学报,2013,32(9):1858-1867.
(LI Shucai,ZHOU Zongqing,LI Liping,et al. Risk Evaluation Theory and Method of Water Inrush in Karst Tunnels and Its Applications[J]. Chinese Journal of Rock Mechanics and Engineering,2013,32(9):1858-1867. in Chinese)
[2]邱龑,杨新安,徐前卫,等. 富水砂层盾构隧道开挖面稳定性及其失稳风险的分析[J]. 中国铁道科学,2015,36(6):55-62.
(QIU Yan,YANG Xinan,XU Qianwei,et al. Analysis on Stability and Instability Risk of Excavation Face of Shield Tunnel in Water-Rich Sand Layer[J]. China Railway Science,2015,36(6):55-62. in Chinese)
[3]陈孟乔. 高水压砂土地层中泥水盾构隧道开挖面失稳机理与风险评估研究[D]. 北京:北京交通大学,2013.
(CHEN Mengqiao. Study on Instability Mechanism and Risk Assessment of Slurry Shield Tunneling Face in Sands under High Hydraulic Pressure[D]. Beijing:Beijing Jiaotong University,2013. in Chinese)
[4]曹成勇. 浅埋透水复合地层泥水盾构开挖面稳定性及掘进参数研究[D]. 长沙:中南大学,2014.
(CAO Chengyong. Study on Face Stability and Tunneling Parameters of Shallow Slurry Shield-Driven Tunnel in Permeable Composite Strata[D]. Changsha:Central South University,2014. in Chinese)
[5]胡欣雨,张子新. 不同地层条件泥水盾构开挖面失稳状态颗粒流模拟方法研究[J]. 岩石力学与工程学报,2013,32(11):2258-2267.
(HU Xinyu,ZHANG Zixin. Research on Particle Flow Approach for Modeling Face Failure Mechanism in Slurry Shield Tunneling under Complex Ground Conditions[J]. Chinese Journal of Rock Mechanics and Engineering,2013,32(11):2258-2267. in Chinese)
[6]JANCSECZ S,STEINER W. Face Support for a Large Mix-Shield in Heterogeneous Ground Conditions[C]// Symposium Tunnelling’94. London:Chapman and Hall Limited,1994:531-550.
[7]ANAGNOSTOU G,KOVARI K. Face Stability Conditions with Earth-Pressure-Balanced Shields[J]. Tunneling and Underground Space Technology,1996,11(2):165-173.
[8]朱伟,秦建设,卢廷浩. 砂土中盾构开挖面变形与破坏数值模拟研究[J]. 岩土工程学报,2005,27(8):897-902.
(ZHU Wei,QIN Jianshe,LU Tinghao. Numerical Study on Face Movement and Collapse around Shield Tunnels in Sand[J]. Chinese Journal of Geotechnical Engineering,2005,27(8):897-902. in Chinese)
[9]秦建设. 盾构施工开挖面变形与破坏机理研究[D]. 南京:河海大学,2005.
(QIN Jianshe. Study on Face Deformation and Collapse of Earth Pressure Shield Tunnel[D]. Nanjing:Hohai University,2005. in Chinese)
[10]徐前卫,朱合华,廖少明,等. 均匀软质地层条件下土压平衡盾构施工的合理顶进推力分析[J]. 岩土工程学报,2008,30(1):79-85.
(XU Qianwei, ZHU Hehua, LIAO Shaoming,et al. Analysis of Reasonable Thrust Force during Tunnel Excavation in Homogeneous Soft Ground by Use of Earth Pressure Balance Shield Machine[J]. Chinese Journal of Geotechnical Engineering,2008,30(1):79-85. in Chinese)
[11]BROERE W. Tunnel Face Stability and New CPT Applications[D]. Netherlands:Delft University,2001.
[12]刘维. 饱和成层土中盾构掘进面稳定理论性研究[D]. 杭州:浙江大学,2013.
(LIU Wei. Research on Tunnel Face Stability in Saturated Layered Soil[D]. Hangzhou:Zhejiang University,2013. in Chinese)
[13]刘栋. 复合地层中土压盾构隧道开挖面稳定性研究[D]. 武汉:华中科技大学,2009.
(LIU Dong. Study on Stability of Tunnel Excavation Face for EBP Shield Machine in Composite Ground[D]. Wuhan:Huazhong University of Science and Technology,2009. in Chinese)
[14]TERZAGHI K. Theoretical Soil Mechanics[M]. New York:John Wiley and Sons Inc,1943:66-76.
[15]王国富,路林海,孙捷城. 突变地质界面围岩稳定性分析及盾构推力判定研究[J]. 岩石力学与工程学报,2015,34(11):2362-2372.
(WANG Guofu,LU Linhai,SUN Jiecheng. Stability of Surrounding Rock and Thrust Calculation of Shield Passing Through Geological Mediums[J]. Chinese Journal of Rock Mechanics and Engineering,2015,34(11):2362-2372. in Chinese)
[16]OBLOZINSKY P, KUWANO J. Centrifuge Experiments on Stability of Tunnel Face[J]. Slovak Journal of Civil Engineering,2004(4): 23-29.
[17]KAMATA H, MASIMO H. Centrifuge Model Test of Tunnel Face Reinforcement by Bolting[J]. Tunneling and Underground Space Technology, 2003, 18(2):205-212.
[18]李君,陈仁朋,孔令刚. 干砂地层中盾构开挖面失稳模式及土拱效应试验研究[J]. 土木工程学报,2011,44(7):142-148.
(LI Jun,CHEN Renpeng,KONG Linggang. Model Test Study of the Failure Mechanism of Shallow Tunnels in Dry Sands[J]. China Civil Engineering Journal,2011,44(7):142-148. in Chinese)
