基于IDDES方法的翼型结冰失速分离流动数值模拟
2016-04-10张恒李杰龚志斌
张恒,李杰,龚志斌
(西北工业大学航空学院,陕西西安710072)
基于IDDES方法的翼型结冰失速分离流动数值模拟
张恒,李杰*,龚志斌
(西北工业大学航空学院,陕西西安710072)
应用基于k-ω SST湍流模型的IDDES(Improved Delayed Detached Eddy Simulation)方法,就失速点附近翼型前缘典型双角状积冰导致的复杂分离流动进行了数值模拟研究。通过与风洞试验结果进行对比,表明对于此类分离流动问题,IDDES方法能够在壁面附近取得良好的速度预测结果,有效解析分离区域内的中小尺度湍流结构,较为准确地描述大尺度时均分离泡的再附位置和形态特征,适用于翼型结冰后复杂流动的精细分析。同时计算结果显示当此带冰翼型位于失速点附近时,角状冰后方脱落剪切层内部的旋涡不稳定析出和输运过程促进了外部流动与回流区域流动间的掺混,将导致流动发生非定常再附现象。
IDDES;结冰翼型;失速分离;复杂流动
0 引言
翼面结冰对飞机飞行安全会产生严重影响,较强结冰条件下形成的角状或楔状冰将破坏翼型的前缘形状,使其绕流特性显著改变,发生非定常分离和再附现象,形成时均流动分离泡,导致升力系数下降和失速迎角提前[1-2]。对翼型结冰后流场和气动特性变化情况的精确预测依赖于准确把握与分离现象相关的流动特征。特别对于结冰翼型失速点附近的分离流动问题而言,其流场结构较为复杂,存在丰富的旋涡相互作用,非定常效应占主导地位[3-4],这对湍流模拟的精度和可靠性提出了较高的要求。但由于工程领域常用的雷诺平均(RANS)方法对湍流脉动信息采用时均化处理方式,难以对此类复杂分离流动的细节特征进行合理描述,需要应用更符合物理事实、精度更高的湍流数值模拟方法。
近年来发展的DES[5](Detached Eddy Simulation)类混合方法能够在一定程度上兼顾分离流动的计算精度和求解效率。其基本思想是利用RANS湍流模型中包含的长度尺度项构造某种混合长度尺度,以使湍流模型在壁面附近区域体现RANS方法的性质,在使用薄层网格的前提下避免近壁面雷诺应力损失,同时降低对计算资源的要求;在以大涡输运为主要特征的远离壁面流动分离区域则体现大涡模拟(LES)方法的特点,使当地雷诺应力快速降低,对大尺度湍流结构进行解析求解,保证空间湍流运动模拟的精度。
目前,利用DES类方法对翼型结冰后流动进行分析的相关研究工作已经取得了一定进展。Mogili[6]等运用DES方法研究了失速点附近结冰翼型的气动特性,证明对于此类问题DES方法较RANS方法能够取得更好的气动力预测结果;Thompson[7]等对不同迎角下的翼型结冰后流动问题做了较为系统的DES分析研究,阐述了网格尺度对数值模拟结果的影响,认为在较大迎角下DES方法对于流动分离特性的模拟精确程度尚有所欠缺;Lorenzo[8]等分别采取DES和DDES[9](Delayed Detached Eddy Simulation)方法对平尾翼型结冰失速前后的流场特征进行了分析,同样指出以上数值方法对于结冰后分离流动的精确预测尚存在一定不足。
针对DES类方法存在的相关问题,Travin[10]等将DDES方法与LES壁面模型(Wall-Modelling in LES,WMLES)相结合,提出了IDDES方法。该方法有利于分离区域内中小尺度湍流结构的充分解析,同时在附着和分离流动并存的过渡区域能够取得更为满意的结果。已经证明该方法对于干净翼型失速分离问题的分析是适用的[10],但与结冰失速分离流动相关的应用研究还并不充分。
本文基于IDDES方法就翼型前缘角状冰导致的失速点附近流动分离问题进行数值模拟研究,以期检验数值方法对此类分离流动的模拟能力,探讨翼型结冰影响流场特征的相关物理机制,为DES类方法在结冰后翼型/机翼气动力分析中的实际应用提供参考。
1 计算模型及网格
针对一种通用航空公务机使用的翼型GLC305开展计算分析研究,翼型前缘具有结冰时间为22.5 min的典型双角状积冰[11]。积冰上下角状结构与翼型表面近似垂直,高度分别约为翼型弦长c的3%和2%。图1描述了该角状积冰的几何形状。
Broeren[12]等在NASA Langley低湍流度风洞(LTPT)针对该翼型前缘结冰后的气动力变化问题进行了多组试验。本文选取的计算状态来流马赫数Ma =0.12,基于翼型弦长的雷诺数Re=1.8×106,来流迎角α=6°,对应风洞试验失速点附近状态。

图1 GLC305翼型前缘双角状积冰Fig.1 Horn ice on the leading edge of GLC305 airfoil
对该带冰翼型三维几何模型生成多块点对接结构化网格,采用图2所示的C-H型网格拓扑结构,展向长度取0.5c。根据Spalart[13]的观点,应用DES类方法进行计算时,计算域可分为欧拉区域(ER)、大涡模拟区域(LR)及雷诺平均区域(RR)三类,需要根据当地流动特征设置不同的网格尺度,各区域的详细定义见文献[13]。图2给出了计算域分区及相应的网格布置情况。
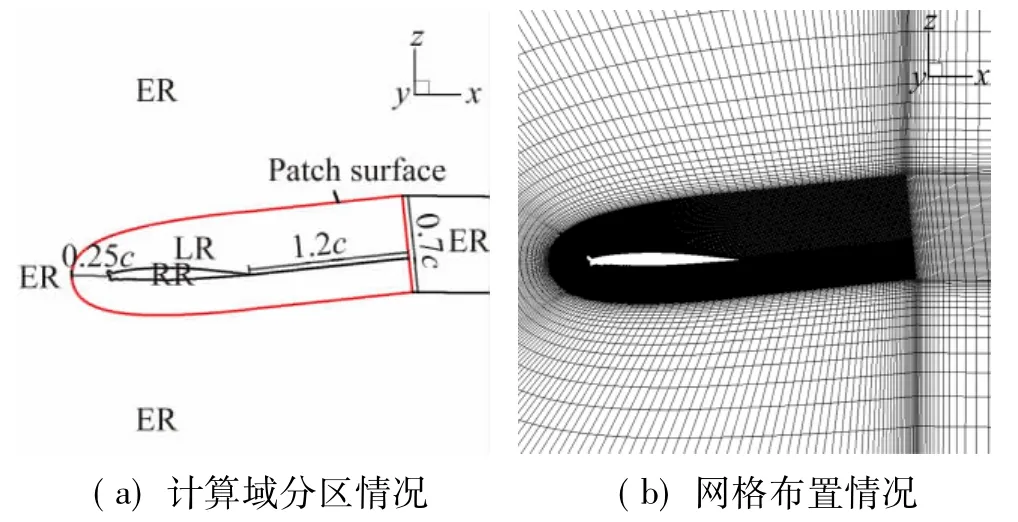
图2 计算域分区及相应的网格布置Fig.2 Com putational region and corresponding grid
为达到节省计算资源的目的,对ER区域和LR区域使用不同周向密度的网格,在区域交界面处采用面搭接技术进行流场信息传递,图2中的红色实线表示网格搭接面位置。搭接面附近的网格布置情况如图3所示。

图3 搭接面附近网格空间截面Fig.3 Com putational grid near the patch surface
在翼型上表面LR区域内布置三向同性网格单元,单元尺度取0.5%c。在物面附近RR区域内布置薄层网格单元,首层网格到壁面的法向距离为1× 10-5c,增长率取1.1,以保证壁面附近y+值不大于1。计算域内网格结点总数约为1.6×107。流动关注区域附近计算网格如图4所示。

图4 流动关注区域附近计算网格Fig.4 Computational grid of the focus region
计算域远场给定无反射边界条件,物面采用绝热、无滑移和法向零压力梯度条件,展向设置周期性边界条件。
2 数值模拟方法
2.1 控制方程及其离散
在有限体积法基础上,对三维可压缩非定常N-S方程进行求解:

其中Q为守恒变量,F、G、H为三向无粘通量,FV、GV、HV为三向粘性通量。对无粘通量项采用Roe-MUSCL三阶迎风通量差分分裂格式,粘性通量项采用二阶中心差分格式进行空间离散;时间推进采用二阶隐式近似因子分解方法。
2.2 湍流模拟方法
根据文献[10]对IDDES方法进行构造,实现湍流数值模拟。该方法基于k-ω SST两方程湍流模型[14],相对DDES方法的主要改进内容包括通过引入壁面距离和网格间距参数对亚格子尺度进行重新定义;以及将DDES方法用作一种WMLES构造了RANS/LES混合长度尺度。
2.2.1 亚格子尺度重新定义
LES方法中常将亚格子尺度取为网格单元体积的立方根,而在DES方法中将其取为网格单元三向长度的最大值。但在以上两种亚格子尺度定义方式中,对各向同性和自由剪切等不同性质的湍流流动,最优亚格子应力模型常数需要取不同的值,对一般情况下的湍流数值模拟缺乏普遍适用性。针对该问题,文献[10]中重新定义了一种亚格子尺度:
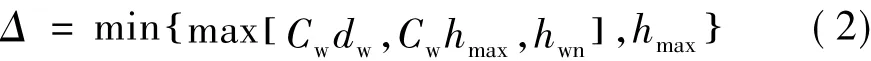
式(2)中hwn为沿壁面法向当地网格单元尺度,Cw为由LES解得到的经验常数,hmax为网格单元三向最大尺度,dw为网格单元与壁面距离。
2.2.2 RANS-LES混合长度尺度构造
基于上述重新定义的亚格子尺度,构造一种新的湍流混合长度尺度。该混合长度由RANS长度尺度和LES长度尺度两部分构成。通过引入该长度尺度定义,壁面附近分离区域的湍流信息能够得到充分解析,并且能够解决DES类方法直接应用于WMLES时产生的对数不连续问题[15]。
对于本文使用的SST湍流模型,该混合长度尺度具备如下形式:

式中lRANS为RANS长度尺度,Δ为式(2)所定义的亚格子尺度,CDES为亚格子应力模型常数。函数frestore和fhyb的具体形式见文献[10]。
3 计算结果与分析
非定常计算设置无量纲时间步长Δt*=0.0025,等价于物理时间步长Δt=0.067ms,每时间步内取15步牛顿子迭代。首先基于非定常RANS方法获得充分发展的初始流场,在初场基础上进行后续IDDES计算至非定常流场基本稳定,以有效滤除分离区域的RANS效应。
以下分别从时均角度和瞬态角度对IDDES计算结果分别进行分析,并与LTPT风洞试验结果[12]及相同网格布置下的非定常RANS方法计算结果进行比较。以对IDDES方法关于此类分离流动的模拟能力进行较为全面的评估和考核。
3.1 时均结果
图5给出了IDDES方法计算基本稳定阶段所得气动力系数的时间序列,图中实线表示各气动力系数瞬时值,虚线表示气动力系数时间平均值。序列的不规则锯齿状分布反映流场中存在强烈的非定常脉动现象,表明数值方法具备对流场内部中小尺度的湍流细节变化进行捕捉的能力。
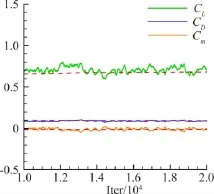
图5 气动力系数时间序列Fig.5 Time history of aerodynam ic force coefficients
表1将计算所得的时均宏观气动力与试验值进行了对比。由表1可知IDDES方法较RANS方法在升力量值预测上有一定提升,表明IDDES方法能够更为准确地反映翼型表面的压力分布特征。阻力量值预测结果精度则与RANS方法相当。

表1 宏观气动力时均计算结果对比Table 1 Comparison of time-averaged aerodynam ic force
图6给出了计算所得时均流场压力分布与试验结果的对比情况。由图6可知RANS方法无法反映因大尺度时均分离泡存在而形成的压力平台。IDDES方法计算所得压力平台长度能够与试验值良好吻合;但压力恢复过程相对试验结果则略为陡峭,该特点在Alam[16]等的DDES方法计算结果中也有所体现。在翼型下表面的局部分离区域内,两种方法同试验结果的吻合程度均较为良好,显示了IDDES方法对近壁面弱分离流动计算的可靠性。不过IDDES方法在翼型后缘的压力分布计算结果较试验值有所偏移,Thompson[7]等利用DES方法也得到了相似的压力分布情况,这与翼型干净无冰情况下的试验结果比较接近。

图6 时均流场压力分布对比Fig.6 Com parison of tim e-averaged pressure distribution
图7展示了时均流场速度分布对比情况,其中分离泡平均外廓和流动平均再附位置由0速度等值线描述。PIV试验测量得到的再附线位置约为53%c附近。由图可知,RANS计算所得分离泡形状和体积与试验结果存在较大差异,流动直到翼型后缘附近才发生再附。与之相较,IDDES计算所得流动再附位置约为50%c处,与试验结果大体相同;分离泡形状与试验结果较为相似,体积与之相当。不过在10%c附近,计算所得回流区域的强度与试验结果仍存在一定差距。

图7 时均流场U向速度分布对比Fig.7 Comparison of time-averaged U velocity contours
图8以流线形式直观给出了不同数值方法计算所得的时均分离泡,并指示了分离泡的时均再附位置。可见IDDES方法有效描述了分离泡的几何形状和再附形态。
图9对比了翼型上表面附近不同位置的时均速度型计算结果。图9(a)给出的速度型位于分离泡起始产生区域,描述了壁面附近的强回流趋势;IDDES方法略为保守地估计了流动速度沿法向的变化,这与Alam[16]等利用动态RANS/LES混合方法和DDES方法给出的计算结果较为相似。图9(b)反映了翼型中部再附区域(0.4<x/c<0.6)的速度分布;IDDES计算结果与试验值吻合良好,显示了精确预测流动再附位置的能力。图9(c)和图9(d)体现了再附区域下游充分发展的附着流动速度分布,IDDES方法预测结果趋势与试验值相一致;但在壁面附近过于乐观地估计了流动速度的恢复情况。总体而言IDDES方法能够在壁面附近区域较RANS方法提供更为良好的速度分布预测结果,这与图7提供的宏观速度分布结果相吻合。

图8 计算所得时均分离泡形状对比Fig.8 Comparison of time-averaged separation bubble
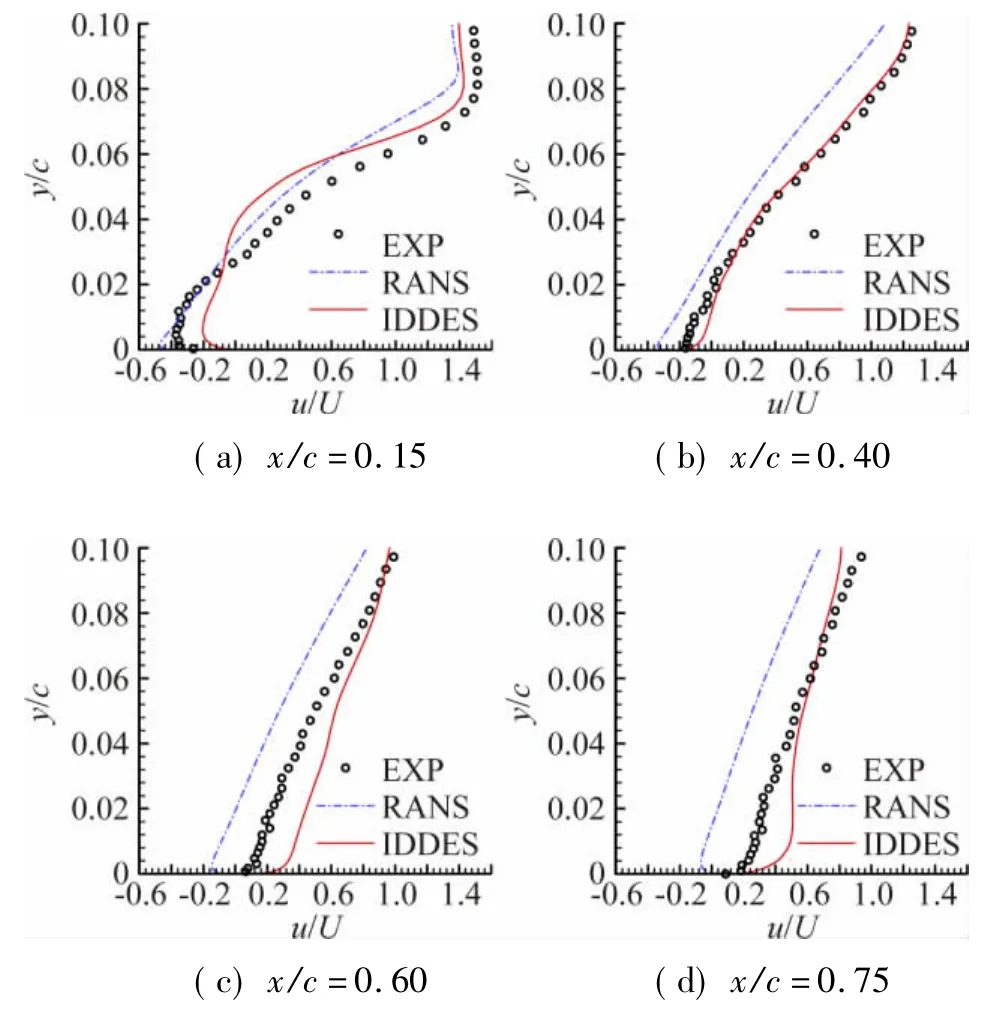
图9 时均流场近壁面不同位置速度型对比Fig.9 Comparison of time-averaged velocity profiles at different stations near the wall
3.2 瞬态结果
图10给出了计算所得瞬态流场展向涡量分布情况。RANS计算结果中角状冰后方的脱落剪切层一直延伸到翼型中部位置,并未显示析出旋涡的趋势,这与真实流动现象是不相符的,表明分离区域湍流涡粘系数过高。而IDDES计算结果中剪切层失稳破碎的起始位置靠近翼型前缘,能够体现外部流动与回流区域切向速度差导致的强烈剪切效应。表明在该算例当中IDDES方法能够有效和快速地降低壁面附近分离区域的涡粘系数水平,减少其对流场细节求解的影响。注意剪切层失稳大约起始于25%弦长左右,与试验结果中的压力恢复起始位置相当,表明压力恢复的直接原因是角状冰后方脱落剪切层的破碎和旋涡析出过程。
此外,IDDES方法在分离区域能够获得比较丰富的旋涡结构。表明计算网格的单元尺度基本能够满足LR区域精细解析湍流结构的要求。由图10可知,旋涡向壁面的输运促进了外部流动与回流区域流动的掺混,使得流动在翼型表面发生再附。由于旋涡的析出和输运过程具备相当程度的随机性,使得再附位置并不稳定于翼型表面,而是在一定范围内振荡,形成再附区域,令分离泡的体积和形状都随时间发生变化。这种再附位置的低频变化是导致文献[3]中提到的结冰翼型气动力特别是升力波动的主要原因。
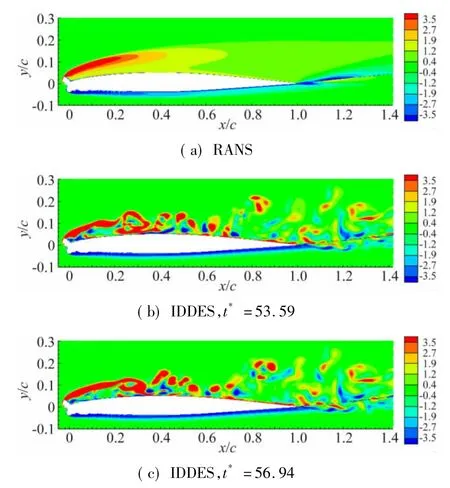
图10 瞬态流场展向涡量分布对比Fig.10 Comparison of instantaneous spanw ise vortices distribution
图11给出了不同时刻计算所得瞬态Q等值面分布,Q准则由Hunt[17]等提出,用于表示流场中旋涡旋转量和拉伸量间的关系。由图11可知,IDDES方法在关注区域内不仅能够获得流场中主要的三维大尺度湍流结构,也能够捕捉到更加细微的中小尺度结构,精确描述了剪切层沿弦向逐步失稳破碎,内部旋涡脱落滚转进入下游的过程;并且处于网格加密区域内的流动尾迹仍大体能够被较为完整地加以解析。由图中同样能够观察到分离泡的形状及再附位置随时间的变化情况。


图11 不同时刻IDDES计算所得瞬态Q等值面分布(Q=0.1)Fig.11 Instantaneous Q criterion of IDDES in different times(Q=0.1)
4 结论
在IDDES方法的基础上针对GLC305翼型失速点附近前缘角状冰诱导产生的分离流动进行了数值模拟研究,并与NASA LTPT风洞试验结果进行了对比。数值模拟结果表明:
1)IDDES方法适用于前缘角状冰导致的翼型失速分离问题的精细数值模拟,较之非定常RANS方法可更好地描述分离流动的物理特征。能够在壁面附近取得良好的速度预测结果,有效解析分离区域内的中小尺度旋涡结构,较为准确地反映大尺度时均分离泡的再附位置和形态特点。
2)对于失速点附近翼型结角状冰引起的流动分离问题而言,由于脱落剪切层内部的不稳定旋涡析出和输运过程促进了外部流动与回流区域流动的掺混,将会导致流动发生非定常再附现象。
[1]Gurbacki H M,Bragg M B.Unsteady flowfield about an iced airfoil[R].AIAA 2004-0562.
[2]Broeren A P,Bragg M B,Addy H E,et al.Effect of high-fidelity ice accretion simulations on the performance of a full-scale airfoil model[R].AIAA 2008-434.
[3]Ansell P J,Bragg M B.Measurement of unsteady flow reattachment on an airfoil with a leading-edge horn-ice shape[R].AIAA 2012-2797.
[4]Ansell P J,Bragg M B.Characterization of ice-induced low-frequency flowfield oscillations and their effect on airfoil performance[R].AIAA 2013-2673.
[5]Spalart P R,Jou W H,Strelets M,et al.Comments on the feasibility of LES for wings and on a hybrid RANS/LES approach[M].Los Angles:Greyden Press,1997.
[6]Mogili P,Thompson D S,Choo Y,et al.RANS and DES computations for a wing with ice accretion[R].AIAA 2005-1372.
[7]Thompson D S,Mogili P.Detached-eddy simulations of separated flow around wings with ice accretions:year one report[R].NASA CR-2004-213379.
[8]Lorenzo A,Valero E,De-Pablo V.DES/DDES post-stall study with iced airfoil[R].AIAA 2011-1103.
[9]Spalart P R,Deck S,Shur M,et al.A new version of detachededdy simulation,resistant to ambiguous grid densities[J].Theoretical and Computational Fluid Dynamics,2006,20(3):181-195.
[10]Travin A K,Shur M L,Spalart P R,et al.Improvement of delayed detached-eddy simulation for LES with wall modeling[C]// European Conference on Computational Fluid Dynamics.The Netherlands:TU Delft,2006.
[11]Addy H E.Ice accretions and icing effects for modern airfoils[R].NASA TP-2000-210031.
[12]Broeren A P,Bragg M B,Addy H E.Flowfield measurements about an airfoil with leading-edge ice shapes[J].Journal of Aircraft,2006,43(4):1226-1234.
[13]Spalart P R.Young-person’s guide to detached-eddy simulation grids[R].NASA CR-2001-211032.
[14]Menter F R.Two-equation eddy viscosity turbulence models for engineering applications[J].AIAA Journal,1994,32(8):1598-1605.
[15]Nikitin N V,Nicoud F,Wasistho B,et al.An approach to wall modeling in large-eddy simulations[J].Physic of Fluids,2005,12 (7):1629-1632.
[16]Alam M F,Thompson D S,Walters D K.Hybrid Reynolds-averaged Navier-Stokes/large-eddy simulation models for flow around an iced wing[J].Journal of Aircraft,2015,51(1):244-256.
[17]Hunt J,Wray A,Moin P.Proceedings of the 1988 summer program[R].Stanford:Center for Turbulence Research,1988.
Numerical simulation of the stall separated flow around an iced airfoil based on IDDES
Zhang Heng,Li Jie*,Gong Zhibin
(School of Aeronautics,Northwestern Polytechnical University,Xi’an710072,China)
The accurate prediction of complex flow phenomena leading by ice accreting of airfoils demands the improvement of turbulent flow prediction methods.The improved delayed detached eddy simulation(IDDES)based on the SST turbulent model is applied in the study of numerical simulation about complex stall separation flow cased by a typical dual horn ice on the leading edge.Comparing with the experimental measurements,numerical simulation results show that IDDES can achieve good prediction results near the wall,effectively resolve middle and small scale vortex structures in the flow separation area and more accurately describe the reattachment position and shape characteristics of the large scale time-averaged separation bubble for such separation flow problem.It is demonstrated that the method is suitable for the analysis of the complex flow after the airfoil icing.At the same time,the calculation results show that when the iced airfoil is near the stall point,the unstable vortex separation and transport process of the shear layer behind the horn ice promote the mixing between the external and reversing flow regions.This effect leads the unsteady reattachment phenomenon of separated flow.
IDDES;iced airfoil;stall separation;complex flow
V211.3
A
10.7638/kqdlxxb-2015.0223
0258-1825(2016)03-0283-06
2015-12-21;
2015-12-28
国家自然科学基金(11172240);国家重点基础研究发展计划(2015CB755800);航空科学基金(2014ZA53002)
张恒(1992-),男,博士研究生,研究方向:计算流体力学.E-mail:qwedc0919@163.com
李杰*(1969-),男,教授,博士生导师.E-mail:lijieruihao@163.com
张恒,李杰,龚志斌.基于IDDES方法的翼型结冰失速分离流动数值模拟[J].空气动力学学报,2016,34(3):283-288.
10.7638/kqdlxxb-2015.0223 Zhang H,Li J,Gong Z B.Numerical simulation of the stall separated flow around an iced airfoil based on IDDES[J].Acta Aerodynamica Sinica,2016,34(3):283-288.
