几何平移 快捷解题
2016-04-09李庆社
□李庆社
几何平移快捷解题
□李庆社
利用图形平移变换可以将几何题中分散的条件汇聚到一个基本图形中,也可以将题目中比较隐蔽的条件明朗化.下面本文略举几例说明.
例1某商场重新装修后,准备在大厅的主楼梯上铺设一种红色的地毯,已知这种地毯的批发价为每平方米40元,已知主楼梯道的宽为3米,其侧面如图1所示,则买地毯至少需要多少元?

图1
解析:先利用平移的知识分别将地毯水平方向的线段沿竖直方向平移到BC上,竖直方向的线段沿水平方向平移到AC上,于是铺地毯的长度之和至少为5.6米+2.8米=8.4米,地毯的总面积为8.4米×3米= 25.2平方米,所以购买地毯至少需要25.2×40=1008元.
点评:此题若逐步计算,比较复杂且不易算出,若运用平移的知识解题,则问题就变得容易多了.
例2某数学兴趣小组开展动手操作活动,设计了如图2所示的三种图形,现计划用铁丝按照图形制作相应的造型,则所用铁丝的长度关系是().
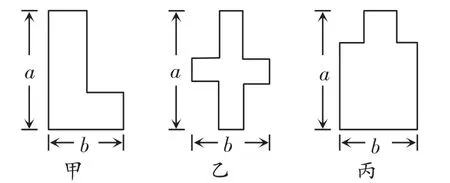
图2
A.甲种方案所用铁丝最长
B.乙种方案所用铁丝最长
C.丙种方案所用铁丝最长
D.三种方案所用铁丝一样长
解析:将甲、乙、丙三种图形中的线段向四周平移,可得这三种图形最终可形成同样大小的矩形,故甲、乙、丙三种方案所用铁丝长度均为2a+2b.故选D.
点评:利用平移的性质得出各图形中所用铁丝的长度是解题关键.
例3如图3,多边形的相邻两边互相垂直,则这个多边形的周长为().

图3
A. 21B. 26
C. 37D. 42
解析:把所有的短横线移动到最上方的那条横线上,再把所有的竖线移动到左、右两条竖线上,这样可以重新拼成一个长方形,如图4,故多边形的周长为2×(16+5)= 42.故选D.

图4
点评:通过将原图形中不规则的边局部平移,从而构成规则的图形是解这类题的关键.
例4如图5,在长方形ABCD中,横向阴影部分是长方形,另一阴影部分是平行四边形,根据图中标明的数据,其中空白部分的面积是多少?

图5
解析:四个空白四边形经过平移可以组成一个长方形,其长为ac,宽为b-c,所以空白部分的面积为(a-c)(b-c).
点评:这里通过平移变换,避免了对图形的分割,使求解简捷、方便.
例5如图6,A、B两地之间有一条国道,国道的宽为a,现要在国道上修建一座垂直于国道的立交桥,使通过A、B两地的路程最近,请你设计建桥的位置,并说明理论依据.
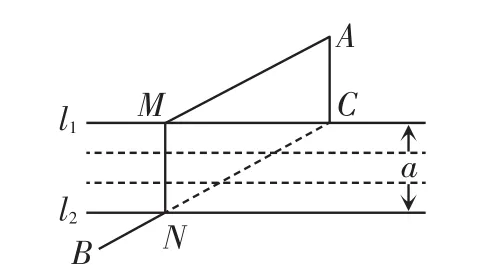
图6
解析:不妨设国道的两边分别为l1,l2,桥为MN,那么从A到B要走的路线就是A→M→N→B了.如图6,MN=a为定值,于是要使路径最短,只要AM+BN最短即可.此时两线段应在同一平行方向上,若设想先过桥,即平移MN于AC,从C到B应是余下的路程,连接BC即为最短的线段,这就说明线段BC与国道边缘l2的交点N就是修桥的位置.
点评:本题是设计建桥的位置,却隐含了平移的知识,体现了数学知识与社会生活的紧密联系.
