巧作辅助线妙解题
2016-04-09辛贺华
□辛贺华
巧作辅助线妙解题
□辛贺华

人教版数学课本习题7.2第9题:如图1,AB∥CD,∠BAE=∠DCE= 45°.填空:因为AB∥CD,所以∠1+45°+∠2+45°=180°.所以∠1+∠2=90°.因为∠1+∠2+∠E=180°.所以∠E=90°.
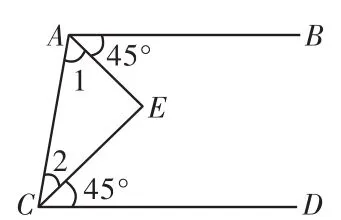
图1
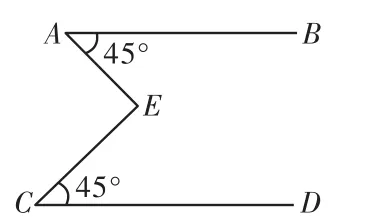
图2
其实这道题可以看作是:如图2,已知AB∥CD,∠BAE=∠DCE= 45°.求∠E的度数.
课本的解题方法是通过作辅助线,连接AC,利用平行线的性质定理和三角形内角和定理解题.
应用到的基础知识有:
1.平行线的性质定理:两条直线平行,同位角相等;两条直线平行,内错角相等;两条直线平行,同旁内角互补.
2.三角形内角和定理:三角形的三个内角的和等于180°.
除了教材的解法外,还可以采用如下解题方法.
解法1:如图3,过点E作直线l,使l∥AB,根据平行公理的推论,因为l∥AB,AB∥CD,所以AB∥CD∥l.因为l∥AB,∠BAE=45°,所以∠1= 45°.因为CD∥l,∠DCE=45°,所以∠2=45°.∠AEC=∠1+∠2=45°+45°=90°.

图3

图4
解法1用到了平行公理的推论:如果两条直线都与第三条直线平行,那么这两条直线也相互平行.
解法2:如图4,延长AE交CD于点F,因为AB∥CD,∠BAE=45°,所以∠EFC=45°,所以∠CEF=180°-∠ECF -∠EFC=90°.所以∠AEC= 180°-∠CEF=90°.
解法2还用到了邻补角的性质:邻补角互补.
解法3:如图5,过点E作直线FG交AB于点F,交CD于点G.因为AB∥CD,所以∠1+∠FGC=180°.又因为∠BAE=∠DCE=45°,由三角形内角和定理知:(∠1+∠BAE+∠2)+(∠3+∠DCE+∠FGC)= 180°×2=360°,所以∠2+∠3= 360°-45°-45°-180°=90°,所以∠AEC=90°.

图5
规律总结:求一个角的度数,经常需要用到平行线的性质定理、三角形内角和定理等知识,这时我们要根据需要添加辅助线,构造平行线或构造三角形去解题.
下面我们再来看一看由课本习题演变成的中考题:
例1如图6,直线l1∥l2,且l1,l2被直线l3所截,∠1=∠2=35°,∠P= 90°,则∠3=_______.

图6
解析:如图6,∠2=35°,∠P= 90°,由三角形内角和定理知:∠4= 55°.因为l1∥l2,所以∠3+∠4+∠1+∠2=180°,所以∠3=180°-∠1-∠2-∠4=180°-35°-35°-55°=55°.
例2如图7,在△ABC中,∠C=90°.若BD∥AE,∠DBC=20°,则∠CAE的度数是().
A. 40°B. 60°
C. 70°D. 80°

图7

图8
解析:如图8,过C作CF∥BD.因为CF∥BD,BD∥AE,所以BD∥AE∥CF.因为CF∥BD,∠DBC= 20°,所以∠BCF=20°.因为∠BCA= ∠BCF+∠FCA=90°,所以∠FCA= 90°-20°=70°.因为AE∥CF,所以∠CAE=∠FCA=70°.答案为C.
