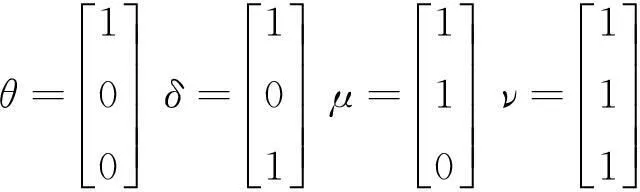一种基于MapReduce的压缩矩阵关联规则挖掘算法

安建瑞，王海鹏，张龙波，金　超，怀　浩

(山东理工大学 计算机科学与技术学院，山东 淄博　255049)



一种基于MapReduce的压缩矩阵关联规则挖掘算法

安建瑞，王海鹏，张龙波，金超，怀浩

(山东理工大学 计算机科学与技术学院，山东 淄博255049)

摘要：提出一种基于MapReduce的压缩矩阵关联规则挖掘算法FMA_Mining。该算法将数据库映射为布尔矩阵，在矩阵映射过程中引入Flag标识，对于连续出现的项用Flag标识标明，简化矩阵元素的读取和列向量运算。针对大数据应用中事务和项目规模较大的情况，算法引入了矩阵分割和并行化处理思想。在Hadoop平台采用WebDocs数据集对算法性能进行测试，从理论分析和实验结果两方面证明了FMA_Mining算法的有效性。

关键词：压缩矩阵；关联规则； MapReduce；Hadoop

关联规则(association rule)是数据挖掘的重要研究领域之一，能够通过对数据库中频繁项集的挖掘，找出不同项目之间的联系。文献[1]中Huang等首次提出基于矩阵的关联规则挖掘算法，称之为BitMatrix Algorithm。该算法把数据库中的事务和项转化为布尔矩阵，只需要扫描一次数据库，不会产生大量的候选集。

文献[2]中Krajca等提出了一种基于因式分解的类布尔矩阵算法，利用频繁闭项集作为候选因子项，然后计算增量连接项目的剩余因素项。该算法能够在保持高准确度的前提下，最大限度地减少数据集的维度。文献[3]中提出了基于MapReduce的矩阵算法，通过Hadoop平台实现矩阵运算的并行化，能够处理规模较大的数据，算法执行效率较高。

文献[4]提出了一种利用压缩矩阵的方法产生频繁项集的算法，在原有的布尔矩阵的基础上，引入了新行Vs和新列Hs，分别表示某一项目的支持度和某一事务中存在的项目个数。每次挖掘频繁项集，动态地计算Vs和Hs的值，将不满足预先设定支持度阈值的行或列删掉。

文献[5]提出了一种NCMA矩阵算法，该算法在矩阵存储、项目分类、压缩矩阵、支持度计算和算法停止条件等方面进行改进，能够减少扫描矩阵的次数，使挖掘频繁项集的效率得到提高。文献[6]提出了一种面向查询扩展的矩阵加权关联规则算法，算法采用4种剪枝策略，使得挖掘效率得到较大提高。

这些基于矩阵的关联规则挖掘算法能够减少扫描数据库的次数，提高挖掘频繁项集的效率，但是仍然存在着一些问题：① 在计算支持度的过程中需要多次扫描矩阵；② 在减少频繁候选集数量的同时，算法计算过程变得过于复杂；③ 由于压缩矩阵不够充分，往往需要存储和计算一些与产生频繁项集无关的元素，这对于频繁更新的事务数据和事务规模较大的情况，是不切实际的；④ 由于设计的算法过于复杂，对于高强度和大批量的事务数据库，矩阵将占用大量的内存空间，很容易引发内存溢出的问题；⑤ 算法没有实现并行化。

本文提出的基于压缩矩阵的关联规则算法FMA_Mining，只需要对数据库进行一次扫描，将数据库映射为0-1矩阵，在矩阵映射过程中引入Flag标识，对于连续出现的项用Flag标识标明，简化矩阵元素的读取和列向量的“与”运算。再通过对矩阵的多次扫描和剪枝，得到频繁项集。

1FMA_Mining算法

1.1算法相关定义

为了更好地说明FMA_Mining算法的过程，首先做出以下定义：

定义1布尔矩阵中，项Ii与Ij的支持度即Ii与Ij在同一水平列上均出现“1”的次数，即Ii与Ij按位相与后求和。项集{Ii,Ij}的支持度记为：

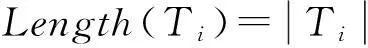
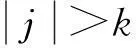
1.2FMA_Mining算法过程描述

1) 根据事务数据库，产生布尔矩阵，进行剪枝和计算，生成频繁1-项集：若项目i出现在某一事务j中，则该布尔矩阵中第i列第j行为“1”，若没有出现，则该布尔矩阵第i列第j行为“0”。布尔矩阵中，一行对应于数据库中的一个事务，一列表示某一项目在各个事务中的存在情况。通过统计每一列中“1”出现的次数，可以求出各个项目的支持度。将各个项目支持度与预定的最小支持度进行比较，进行剪枝操作，删掉不满足阈值的向量。

2) 在生成布尔矩阵G的过程中引入Flag标识，当某一列的第i行是“0”元素，将Flag标识定位在该列的第i行处，继续考察该列第i+1行元素，如果该i+1行元素依然为“0”，继续考察第i+2行元素，直到该列结束或者该列某一行出现元素“1”。将该列第i行处的元素“0”用元素“F”代替，将该列第i+1行处的元素“0”用出现连续“0”的次数m代替，表示该列第i行开始出现连续m个的“0”元素；同理，元素“T”表示该列出现连续的“1”元素，将该列第i+1行处的元素“1”用出现连续“1”的次数n代替。由于“F”和“0”元素连续出现的次数以及“T”和“1”连续出现的次数均占用两个元素位置，所以默认引入Flag标识的列中“0”或“1”连续出现的次数应在3次以上。

在后续的矩阵运算中，当扫描到某一列出现元素“F”或者元素“T”，可以直接跳过该连续“0”元素或者“1”元素区间，减少对矩阵元素的读操作；在挖掘频繁k-项集时，进行矩阵列向量的运算时，只要任何一个列向量读到标识“F”，则列向量中与标识“F”下连续“0”的同等数量的行可以直接剪掉。

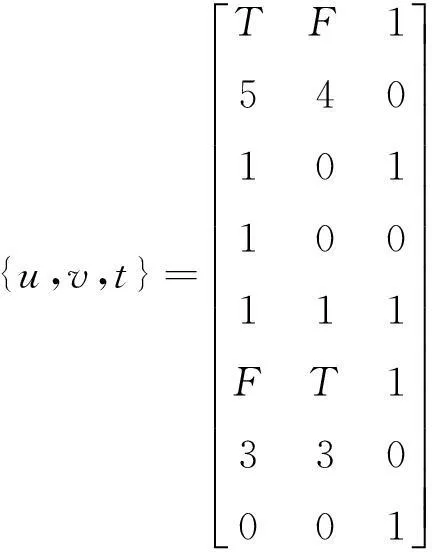
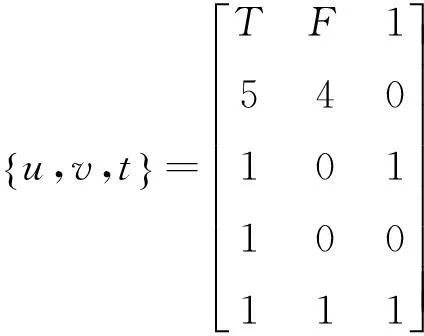
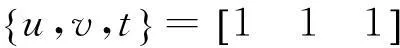
3) 利用频繁1-项集进行自连接，对生成的两列向量进行与运算，得到各候选项集的支持度。通过与最小支持度进行比较，得到频繁2-项集。

4) 利用定义3对得到的频繁2-项集进行裁剪。如果某个项目在频繁2-项集出现的次数小于2，则删除掉包含该项目的所有频繁2-项集，从而得到新的频繁2-项集。

5) 利用步骤4中得到的频繁2-项集得到频繁3-项集，依次类推，直到得到频繁k-项集。

1.3FMA_Mining算法伪代码描述

输入：事务数据库D，最小支持度计数值Min_Sup；

输出：D中所有满足最小支持度计数值的频繁项集

1) 构建布尔矩阵并剪枝，生成频繁1-项集，引入Flag标识

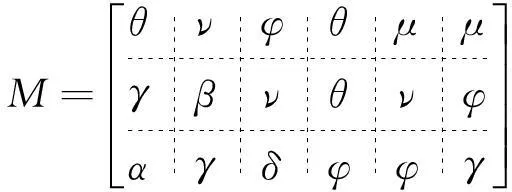
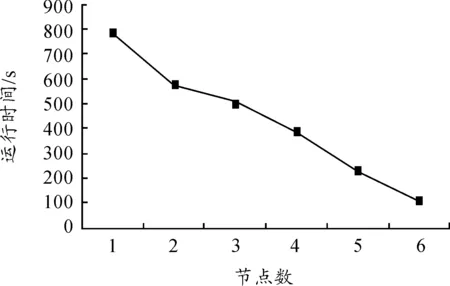
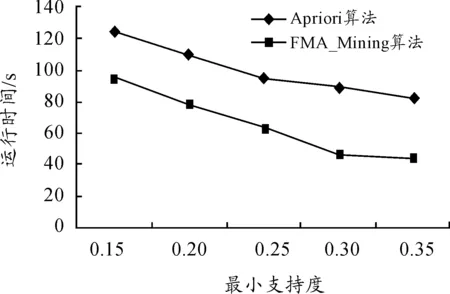
for(int j=0;j

L1-count=0;

for(int i=0;i

//构造0-1矩阵

if(D[i][j]!=NULL){

L1-count++; A[i][j]=1;}

if(D[i][j]==NULL){

A[i][j]=0;

if(Flag==false){

//引入Flag标识

启动Flag标识和计数器；

}

}

if(L1-count>=Min_Sup){

//生成频繁1-项集

L1= L1∪{A[i]}

}

}

end;

2) 生成频繁k-项集

k=1;

do{//直到无法找出频繁项集

for all ItemValue{i1,i2,…,ii}∈Lk

for all ItemValue{i1,i2,…,ij}∈Lk

if(all is 1:A[1] &&A[1]>=Min_Sup∧each A[2] &&A[2]>=Min_Sup∧…∧each A[j] &&A[j]>=Min_Sup){

对形成的频繁项集进行剪枝；

Lk+1= Lk∪{Ii∪Ij}

}

}while(Lk!=Φ)

end;

其中：D[i][j]表示数据库中第i条事务的第j个项；A[j]表示布尔矩阵的第j列；∧表示按位与运算。

2大数据集下FMA_Mining算法的改进

2.1矩阵分块算法的实现

随着事务和项目的不断增长，对于FMA_Mining算法中的标识Flag，可以进行行改造，从而对生成的矩阵进行最大化压缩，为此，做出以下定义：

定义4矩阵的压缩阈值q，q的取值根据事务的数量规模来确定，事务数量越大，q的取值越大。

1) 根据q的值，对矩阵首先进行压缩，对矩阵每一列的q行进行划分，由于矩阵的每个元素都是“0”或“1”，每一个划分后的小区域的类型是可控的，我们用不同的标识代替。

例如，对于拥有9万条事务，100个项目的数据库D，可以设定矩阵压缩阈值q为3，对数据库D生成的矩阵进行划分，可以把原先9万行、100列的矩阵划分成3万*100的小区域矩阵。每个小区域都是由3*1的小矩阵组成，其中小矩阵每个元素都为“0”或“1”，则小区域的类型共有8种。

2) 对矩阵行压缩后，在计算频繁k-项集的时候，只需要对项Ii所在列的小区域进行与运算，对于小区域的与运算，可以提前进行预计算，并存入固定表L中。当需要得知某些小区域的计算结果，只需要进行查表即可。这相当于对矩阵进行了列压缩。

通过分别对矩阵进行行压缩和列压缩，使得FMA_Mining算法在处理大规模数据集下的效率得到很大提高。

2.2矩阵分块算法实例

假定矩阵M是要进行压缩的矩阵，矩阵M为：

取矩阵压缩阈值q为3，对M矩阵进行区域划分后为：

对区域进行标识化处理，标识类型如下所示：

引入以上标识后，转化后的矩阵M如下所示：

对各个标识的与运算结果提前存入表L中，当计算频繁k-项集的支持度时，只需要查表即可。例如，计算M[1]与M[2]的支持度，只需要查表θ∧ν，γ∧β，α∧γ即可。

2.3对矩阵进行MapReduce并行化

对矩阵分块能够极大地压缩矩阵的规模，但是在大数据环境下，数据量的规模十分庞大，序列化的单机读取数据库并进行矩阵转换将使得算法的效率大大降低。为此，将FMA_Mining算法与并行编程模型MapReduce相结合，实现矩阵运算的并行化。算法执行方法如下：

1) 利用MapReduce将原始数据划分为大小相等的N个数据子集，将N个数据子集文件部署在N个机器节点上。

2) 利用Map函数生成〈key,value〉对，其中，key代表事务的编号，value代表每一事务项目的集合。Map函数的伪代码如下：

void Map(key,value){

for 每个TID中的元素Ti

foreach(string w:value)

setNum(1);

for 每个元素Ti的次数

foreach(int w:sum)

sum=sum+1;

if(sum

剪枝：删掉该元素；

}

3) 对N个数据子集文件分别应用FMA_Mining算法，引入Flag标识量和矩阵分块的方法，对每个数据子集进行关联规则挖掘。

4)利用Reduce函数对生成的〈itemsets,frequency〉进行合并，形成全局频繁项目集和输出文件。Reduce函数的伪代码如下：

Reduce(itemSets,sum){

for N个数据子文件生成的关联规则 do

合并结果，删除不满足Min_Sup的频繁项集;

输出结果文件；

}

3实验结果及分析

实验采用Frequent Itemset Mining Dataset Repository的Webdocs作为数据集进行测试，数据集Webdocs包含1 692 080条事务，大小为1.4 GB。实验环境上，建立6个节点的Hadoop集群环境，Hadoop版本为稳定版2.2.0，其中5个节点作为DataNode，CPU是Intel(R) Core(TM) i3-2350M，主频为2.3 GHz，内存2 GB，另一节点是DELL R720服务器，性能较高，作为NameNode。操作系统均为Ubuntu 14.04，JDK版本是1.8.0.51。

首先，测试FMA_Mining算法的并行性能。依次将算法运行在1到6个节点上，考察FMA_Mining算法的运行时间，发现随着节点数目的增加，算法的执行时间明显下降。实验结果如图1所示。

图1　算法并行性实验结果

再次，把Webdocs数据集平均分配到6个节点，在支持度分别为0.15，0.2，0.25，0.3，0.35的情况下，分别考察Apriori与FMA_Mining在不同支持度下的运行时间，结果如图2所示。

图2　算法不同支持度下的实验结果

最后，取定支持度为0.3，依次选取100 000，300 000，500 000，700 000条事务，分别考察Apriori与FMA_Mining在不同数据集规模下的运行时间，结果图3所示。

图3　算法不同数据集规模下的实验结果

4结束语

FMA_Mining算法的时间复杂度为O(IkJ)，其中，I为布尔矩阵的行数，J为布尔矩阵的列数，k为频繁项集的阶数。算法只需要扫描1次数据库，在扫描过程中生成的布尔矩阵置于内存。引入Flag标识后，减少了矩阵的读操作和矩阵列向量的运算，大大减少了系统I/O操作的次数，并且不会产生大量的候选集；基于MapReduce的并行化操作和矩阵分块处理，进一步提升了算法的执行效率。实验结果表明：这种算法降低了算法运行时间，稳定性高，能够提高关联规则在频繁项集上的挖掘效率。

参考文献：

[1]HUANG L S,CHEN H P,WANG X,et al.A Fast Algorithm for Mining Association Rules[J].Journal of Computer Science and Technology,2000,15(6):619-624.

[2]KRAJCA P,OUTRATA J,VYCHODIL V.Using frequent closed itemsets for data dimensionality reduction[C]//11th IEEE International Conference on Data Mining,Institute of Electrical and Electronics Engineers Inc,Vancouver,2011:1128-1133.

[3]YANG X Y,ZHEN L,FU Y.MapReduce as a programming model for association rules algorithm on Hadoop[C]//3rd International Conference on Information Sciences and Interaction Sciences,IEEE Computer Society.Chengdu:IEEE,2010:99-102.

[4]SIHUI SHU.A New Association Rule Mining Algorithm Based on Compression Matrix[J].Computer Engineering and Networking Lecture Notes in Electrical Engineering,2014,277:281-289.

[5]TAOSHEN LI,DAN LUO.A New Improved Apriori Algorithm Based on Compression Matrix[J].Advanced Data Mining and Applications Lecture Notes,2014,8933:1-15.

[6]黄名选,严小卫,张师超.基于矩阵加权关联规则挖掘的伪相关反馈查询扩展[J].软件学报，2009(7)：1854-1865.

[7]MOHANTY A K,SENAPATI M,BEBERTA S,et al.Mass classification method in mammograms using correlated association rule mining[J].Neural Computing and Applications,2013:232.

[8]陈俊明.基于布尔矩阵的空间关联规则提取方法研究[J].测绘与空间地理信息,2014(5):123-126.

[9]黄治国,王淼.基于决策矩阵的可信关联规则挖掘方法[J].计算机工程与设计,2014(8):2890-2895.

[10]Al-DHARHANI G S,OTHMAN Z A,BAKAR A A.A Graph-Based Ant Colony Optimization for Association Rule Mining[J].Arabian Journal for Science and Engineering,2014:396.

[11]ZHANG Lihua,WANG Miao,ZHAI Zhengjun,et al.Mining Closed Strong Association Rules by Rule-growth in Resource Effectiveness Matrix[J].Journal of Software,2014:99.

[12]吕桃霞,刘培玉.一种基于矩阵的强关联规则生成算法[J].计算机应用研究,2011(4):1301-1303.

[13]胡维华,冯伟.基于分解事务矩阵的关联规则挖掘算法[J].计算机应用,2014(S2):113-116.

[14]MARGHNY H.MOHAMMED M,DARWIEESH A B,et al.Advanced Matrix Algorithm (AMA):reducing number of scans for association rule generation[J].IJBIDM,2011:6.

[15]朱清香,侯会茹,刘晶,等.基于矩阵多源加权关联规则在个性化推荐中的应用[J].科技管理研究,2015(1):183-187.

[16]张伟丰,杨丽华.基于矩阵的多段支持度关联规则挖掘算法[J].湖北汽车工业学院学报,2014(2):72-76.

[17]唐冰,陆春芽.一种基于反区分矩阵的多维关联规则挖掘方法[J].广西民族大学学报(自然科学版),2013(1):62-65.

(责任编辑何杰玲)

A Compression Matrix Algorithm for Mining Association Rules Based on Mapreduce

AN Jian-rui, WANG Hai-peng, ZHANG Long-bo, JIN Chao, HUAI Hao

(College of Computer Science and Technology,Shandong University of Technology, Zibo 255049, China)

Abstract:An association rules mining algorithm, FMA_Mining, was proposed based on MapReduce and compression matrix. In this algorithm, databases were mapped into Boolean matrices. In the process of matrix mapping, a flag was introduced to identify the consecutive elements, thus simplifying the reading of matrix elements and operating of column vectors. For the big scale of affairs and projects in big data applications, matrix partition and parallel processing were introduced in the FMA_Mining algorithm. In the Hadoop platform, the performance of the algorithm was tested by using WebDocs data set, and the validity of the FMA_Mining algorithm was proved by both theoretical analysis and experimental results.

Key words:compression matrix; association rule; MapReduce; Hadoop

文章编号：1674-8425(2016)02-0095-06

中图分类号：TP391

文献标识码：A

doi:10.3969/j.issn.1674-8425(z).2016.02.017

作者简介：安建瑞(1990—)，男，硕士研究生，主要从事数据挖掘研究；王海鹏(1980—)，男，博士，讲师，主要从事数据挖掘、生物信息学研究；通讯作者 张龙波(1968—)，男，博士，教授，主要从事数据库理论与应用、数据挖掘研究。

基金项目：山东省自然科学基金资助项目(ZR2014FQ024)

收稿日期：2015-06-15

引用格式：安建瑞，王海鹏，张龙波，等.一种基于MapReduce的压缩矩阵关联规则挖掘算法[J].重庆理工大学学报(自然科学版)，2016(2):95-100.

Citation format：AN Jian-rui, WANG Hai-peng, ZHANG Long-bo, et al.A Compression Matrix Algorithm for Mining Association Rules Based on Mapreduce[J].Journal of Chongqing University of Technology(Natural Science)，2016(2):95-100.