灰色预测GM(1,1)模型的应用及改进

吴志荣

(江苏师范大学，江苏 徐州 221000)



灰色预测GM(1,1)模型的应用及改进

吴志荣

(江苏师范大学，江苏 徐州 221000)

摘要：灰色GM(1,1)预测模型是灰色理论的重要组成部分，它的建立不需要有太多的样本，不要求样本有较好的分布规律，计算量少、有较强的适应性，所以GM(1,1)模型的应用很广泛，本文运用GM(1,1)模型进行实例预测，最后又提出一种改进GM(1,1)模型，大大的提高了该模型对问题的预测精度。

关键词：灰色预测模型；灰色理论;GM(1,1)模型

引言

20世纪80年代初，华中理工大学邓聚龙教授首先提出了灰色系统的概念，并建立了灰色系统理论，引起了国内外很多学者、科研人员的重视。得到了深入的研究，并在众多领域获得了广泛的应用。灰色系统理论在国际上也产生了很大的影响，目前在英、美、德、日等国家，有许多学者从事灰色系统的研究和应用。

1灰色GM(1,1)模型

1.1灰色预测

灰色预测是用灰色模型来进行定量分析的，通过对原始数据的生成处理寻求系统变动的规律，建立起相应的微分方程模型，预测事物未来的发展趋势和未来状态。

1.2GM(1,1)模型的基本原理

设x(0)=(x(0)(1),x(0)(2),…,x(0)(n))为原始数列，它的1次累加生

定义x(1)的灰导数为

d(k)=x(0)(k)=x(1)(k)-x(1)(k-1)

令z(1)=(z(1)(2),z(1)(3),…z(1)(n))为数列x(1)的邻值生成数列，

其中z(1)(k)=αx(1)(k)+(1-α)x(1)(k-1)

定义GM(1,1)的灰微分方程模型为

d(k)+az(1)(k)=b

即x(0)(k)+az(1)(k)=b

其中x(0)(k)称为灰导数，a称为发展系数，z(1)(k)称为白化背景值，b称为内生控制灰数。

将时刻k=2,3,…,n代入(1)式有

引入矩阵向量记号：

数据向量参数向量数据矩阵

于是GM(1,1)模型可表示为Y=Bu.

对于GM(1,1)的灰微分方程，如果将灰导数x(0)(k)的时刻k=2,3,…,n

视为连续变量t，则x(1)视为时间t的函数x(1)(t)，GM(1,1)的灰微分方程

对应的白微分方程为：

令x(1)(t=1)=x(0)(1)为初始值，

综上所述，

得到了GM(1,1)模型的灰色预测模型为：

2实例预测

已知某食品公司2004年-2013年销售额(见表1)，在市场不会出现大的波动情况下，根据前十年的销售额预测该公司未来10年的销售额。

表1　单位：元

运用MATLAB编程如下：

clear

syms a b;

c=[a b]′;

A=[89677,99215,109655,120333,135823,159878,182321,209407，246619,300670];

B=cumsum(A);%原始数据累加

n=length(A);

for i=1:(n-1)

C(i)=(B(i)+B(i+1))/2；%生成累加矩阵

end

% 计算待定参数的值

D=A;D(1)=[];

D=D′;

E=[-C;ones(1,n-1)];

c=inv(E*E′)*E*D;

c=c′;

a=c(1);b=c(2)；

% 预测后续数据

F=[];F(1)=A(1);

for i=2:(n+10)

F(i)=(A(1)-b/a)/exp(a*(i-1)+b/a;

end

G=[];G(1)=A(1);

For i=2:(n=10)

G(i)= F(i)- F(i-1);%得到预测出来的数据

end

编程后预测出以下：

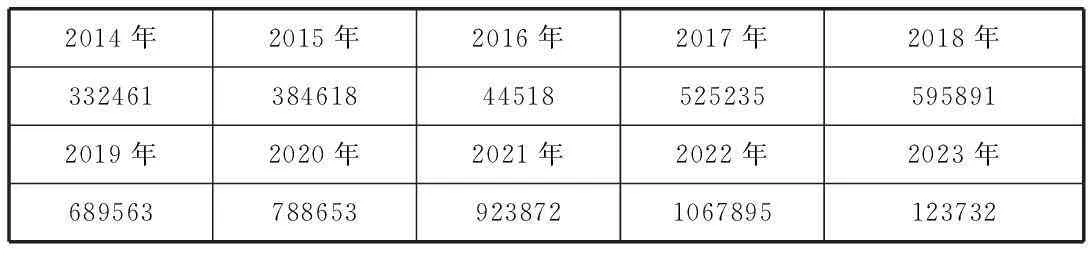
表2　单位：元

3GM(1,1)预测模型的改进

GM(1，1)模型的预测精度与可靠性主要依据原始数据的光滑度和准指数性决定。因此，如何提高原始数据的光滑度，将成为一个技术问题。

由定理如果x(0)(k)为递增数列，并且x(0)(1)≥e，则

对该模型进行进一步的改进，以适应高增长序列数据.

初始值最好取原始数据的最小二乘估计，即

4小结

灰色预测模型是一种典型的预测方法，已经在工业、农业、经济、社会等领域获得广泛应用，但同时也存在一些预测精度不高的情况。近几年，针对这一问题很多学者对GM(1,1)模型提出了各种改进方法，来提高模型的预测的精确度。本文主要对灰色预测的实例应用，对GM(1,1)模型进一步的改进，提高模型的预测精度，将GM(1,1)进一步推广。

参考文献：

[1]邓聚龙.灰色理论基础[M]武汉:华中科技大学出版社,2002.

[2]邓聚龙.灰色系统理论基教程[M]武汉:华中科技大学出版社,1990.

[3]李云贵，李清富，赵国藩．灰色GM(1，1)预测模型的改进[J]．系统工程,1992，10(6)：27-31．

[4]罗荣桂，陈炜．灰色模型的一点改进及应用[J]．系统工程理论与实践，1988(2)：46-52．

[5]张大海，江世芳，史开泉．灰色预测公式的理论缺陷及改进[J]．系统工程理论与实践，2002，22-26

中图分类号:O231

文献标志码：A

文章编号：1671-1602(2016)04-0235-02

作者简介：吴志荣(1989-),女，汉族，河南南乐，研究生，江苏师范大学，研究方向：市场营销。