转动载荷对卫星姿态的影响与控制研究*
2016-04-08王新民褚永辉张俊玲
王新民,褚永辉,张俊玲,袁 军
(1.北京控制工程研究所,北京100190;2.空间智能控制技术重点实验室,北京100190)
转动载荷对卫星姿态的影响与控制研究*
王新民1,2,褚永辉1,2,张俊玲1,2,袁 军1
(1.北京控制工程研究所,北京100190;2.空间智能控制技术重点实验室,北京100190)
研究带有转动载荷和挠性附件的卫星姿态控制问题.基于具有广义坐标形式的牛顿-欧拉方法建立了卫星姿态动力学模型和转动载荷力矩模型,研究载荷产生的动不平衡力矩和静不平衡力矩的机理和特点.分析载荷干扰对卫星姿态的影响特性,给出基于传递函数进行拉氏变换以估算姿态抖动量的方法.分析卫星姿态控制系统设计干扰补偿控制器的条件,给出了控制器的工程设计方法.验证结果表明该方法有效且能提高卫星姿态精度.
静不平衡;动不平衡;转动载荷;干扰补偿
0 引言
随着空间任务需求的不断增长,卫星结构和载荷越来越复杂,姿态控制性能指标越来越高,而且很多卫星带有转动载荷,如海洋水色仪、扫描微波辐射计、微波散射计、微波成像仪、扫描镜等.载荷的运动将带来干扰[1-3],未补偿的干扰将直接作用于卫星平台,这会降低卫星姿态稳定度和指向精度,甚至激发挠性附件(如太阳帆板)的振动,导致卫星姿态振荡,影响成像质量,为此需要研究转动载荷对卫星姿态的影响并采取措施补偿载荷运动产生的干扰[3].
转动载荷产生的干扰主要包含3类:1)载荷工作设计的有规律运动干扰,如匀速运动、加减速运动等带来的角动量变化和干扰力矩;2)载荷的静不平衡干扰;3)载荷的动不平衡干扰.干扰补偿的必要性主要有:1)载荷运动干扰的频率一般大于姿控系统的控制带宽、姿控系统无法自主抑制该干扰;2)采取补偿可避免载荷运动造成的过大干扰进入姿控系统、简化控制系统设计和分析.刘军等[4]根据已知的扫描镜转动运动规律,提出了一种通过设定角动量交换系统标称值条件对卫星进行控制、以及抑制变速转动部件引起卫星姿态扰动的前馈控制方案.王佐伟等[5]针对带有活动有效载荷的航天器,研究了一种基于直接型自适应模糊逻辑和干扰补偿的控制方法,将自适应模糊系统直接用作系统的主控制律,利用扩张状态观测器对模糊系统的逼近误差和内外干扰力矩进行观测并予以补偿.俞洁等[6]通过研究载荷运动部件的规律,提出了一种反馈控制加力矩补偿的方法,给出力矩补偿的设计.上述研究只分析了载荷设计的有规律运动对卫星姿态的影响,干扰补偿技术也是基于该运动规律设计的,没有考虑载荷静不平衡和动不平衡等对卫星姿态的影响.
本文首先给出综合考虑载荷静不平衡、动不平衡和运动特性等卫星动力学和载荷力矩模型,分析了载荷干扰力矩特性及其对卫星姿态的影响,再进行干扰补偿控制器设计,最后给出了数学仿真结果.
1 动力学模型和载荷影响分析
1.1 动力学模型
考虑一类带有运动载荷和挠性附件的卫星姿态动力学模型,将卫星中心体视为刚体,基于具有广义坐标形式的牛顿-欧拉方法建立卫星姿态动力学和载荷转动子体产生的力矩模型.设卫星质心坐标系为Fb,载荷转动子体的固连坐标系为Fp(原点取与固定部分铰链点且在转轴上),ω为卫星绝对角速度在Fb的表示,ωp为载荷转动子体相对卫星本体的转动角速度在Fp的表示,RA为Fp相对Fb的转换矩阵,rA为卫星质心至Fp原点的矢径在Fb的表示,ρA为Fp原点至载荷转动子体质心的矢径在Fp的表示,Is为卫星在Fb的惯量矩阵,IA为载荷转动子体在Fp的惯量矩阵,mA为载荷转动子体质量,H为动量装置的合成角动量列矢量,Tc为姿态控制力矩矢量,Td为卫星的外部干扰力矩矢量,q为挠性附件的模态坐标矢量,B为挠性附件的转动耦合系数矩阵,ζ和Λ分别为挠性附件的结构阻尼矩阵和模态角频率矩阵.(·)×表示矢量形成的反对称矩阵.
卫星动力学方程为
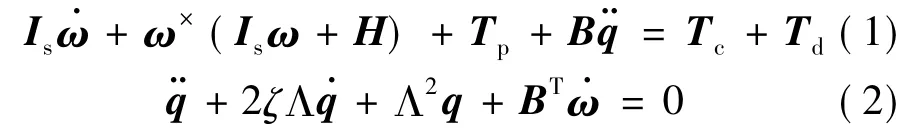
式中Tp为载荷转动子体产生的力矩矢量,不考虑载荷转动对卫星惯量矩阵的影响,则
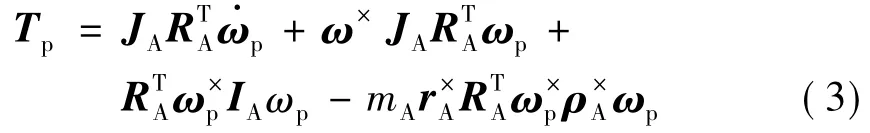
式中JA为载荷转动子体在Fb的惯量矩阵
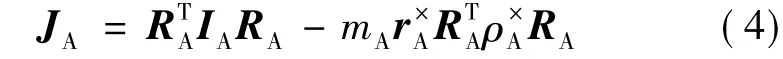
对于三轴稳定姿态控制卫星,卫星相对于轨道坐标系的三轴姿态角一般为小量,相应的姿态角速度可表示为[7]

式中:ω0为卫星轨道角速率,φj和φj分别为卫星j 轴(j=x,y,z)的姿态角和角速度.
1.2 载荷干扰特征
式(3)右端第一项为载荷非恒定转速带来的力矩Tpw,第二项为陀螺力矩Tpg,第三项为动不平衡力矩Tpd,仅与载荷特性相关,第四项为静不平衡力矩Tps,不仅与载荷特性相关而且与其转动子体在卫星的位置相关.由于这四项都与转换矩阵RA相关,而RA又与ωp和时间t相关,因此载荷产生的力矩Tp具有以ωp为基频的周期性变化特点,甚至形成拍频现象.
下面具体分析载荷动不平衡力矩Tpd和静不平衡力矩Tps.不失一般性,假设载荷转动子体绕z轴以转速ωpz旋转.
由式(3)得到动不平衡力矩为

式中:α=ωpzt为转动角度,IAxz和IAyz为惯量矩阵IA的惯性积.以Tpd的滚动分量Tpdx为例,考虑到正弦和余弦可以合成一个单一的谐波项,则

式中:β是相位角,kdb=是动不平衡度,可见动不平衡度与载荷转动子体惯量矩阵的惯性积相关,即反映了质量分布的不均匀性.
由式(3)、(6)和(7)表明载荷动不平衡具有如下特点:1)动不平衡产生与旋转轴垂直的两个轴向正弦力矩;2)力矩大小不仅正比于转速平方,而且正比于动不平衡度;3)多个转动载荷的动不平衡力矩具有相加性;4)加强载荷构型设计、减小动不平衡度,可以减小动不平衡力矩.
由式(3)得到静不平衡力矩为

式中:αx=α+βx,αy=α+βy,βx和βy是相位角,rAj(j=x,y,z)是 rA的j轴分量,ksb=mA是静不平衡度,ρAx和ρAy分别为ρA的x和y方向分量,可见静不平衡度与载荷转动子体的质量和矢径相关,即反映了质量分布的不对称性.
由式(3)和(8)表明载荷静不平衡具有如下特点:1)静不平衡产生三轴正弦力矩;2)力矩大小不仅正比于转速平方,而且正比于静不平衡度,并与载荷安装位置相关;3)多个转动载荷的静不平衡力矩具有相加性;4)加强载荷构型设计、减小静不平衡度,而且优化载荷安装位置,可减小静不平衡力矩.
1.3 载荷对卫星姿态的影响特征
不考虑姿控系统作用,即开环控制状态下,载荷干扰对卫星姿态的影响可近似为

由上述分析和式(9)可知,Tp的周期性变化导致姿态角速度也是周期性变化.应当指出的是,仅当载荷运动比姿控系统的控制带宽要快的时候,上面的近似才有效.在一般情况下,则希望把姿控系统的控制效应考虑在内,卫星姿控系统的控制器一般可以近似为一个二阶系统,卫星j轴(j=x,y,z)从扰动力矩输入到姿态输出的传递函数Gj(s)为
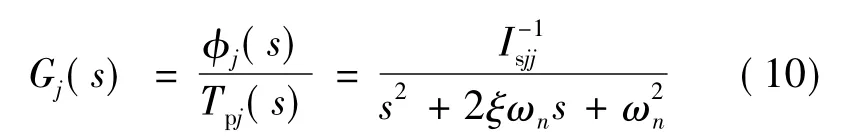
式中:ξ和ωn分别为姿控系统控制器的阻尼比和自然频率,Isjj为惯量矩阵Is的j轴转动惯量,Tpj为Tp的j轴分量.姿控系统的控制带宽ωb一般表示为[8]ωb= ωn若 ξ= 0.707,则ωb=ωn.
根据公式(10)可以估算姿态影响大小或抖动量,不失一般性,将上述周期性变化的Tpj表述为

将式(11)代入式(10),得到

时域稳态响应为

式中:φmj=Twpj|Gj(jωp)|为幅值,βpj为Gj(jωp)的相角.由式(13)可知,载荷对姿态的影响具有周期性.
如果ξ=0.707且ωp≫ωn,由式(13)可得到姿态抖动量的稳态幅值为
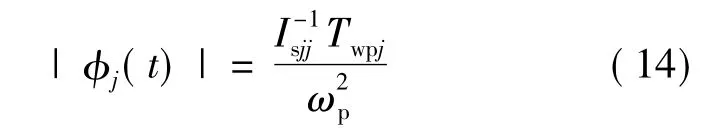
2 干扰补偿控制器设计
由上述分析以及载荷各项干扰力矩Tpw、Tpg、Tpd、Tps的表达式可知,要减小转动载荷对卫星姿态的影响,需要卫星总体、载荷系统和姿控系统在卫星研制过程中统筹考虑和协调设计.载荷系统在产品设计和研制过程要尽量减小静不平衡度和动不平衡度,尽量减少不必要的转速波动.卫星总体要优化指标和频带分配,优化载荷安装位置.姿控系统要做好影响分析,必要时要设计干扰补偿控制器.
从式(13)可知,正弦扰动力矩的稳态输出是一个同频率的正弦信号,这样就为姿控系统实现在轨自主干扰补偿控制带来可能.姿控系统要实现干扰补偿控制首先需要分析控制实现的可行性,主要考虑如下方面:1)姿控系统能提供的有效控制力矩要大于干扰力矩;2)要具备在轨干扰辨识或地面注入干扰模型的功能;3)时滞不会影响姿态指标的实现.只有上述3点满足,姿控系统才具备干扰补偿的能力,否则需要卫星总体和载荷系统协调解决.
考虑设计具有某一个频率ωpk的正弦干扰补偿器如下:

式中:tk为姿控系统时间wpkj为干扰力矩幅值的估计,为可调相位角.Tpkjc可以根据离线姿态数据的分析结果再将各参数注入姿控系统,或者在线通过设计卡尔曼滤波器辨识估计得到.即便干扰补偿器模型准确、控制精准,由式(13)得到,时滞τ带来的姿态和角速度的最大误差近似为

由此可见,时滞对姿态和角速度影响较大,这样干扰控制不仅要求考虑系统时延,而且要求考虑姿控系统的最小姿控时间.系统时延可以通过调整相位角解决,最小姿控时间的设计则需综合姿控系统控制器和姿态指标要求.以姿态角速度为例,工程上最小姿控时间Δtp一般要满足

式中 φnj为要求的姿态角速度指标值.
卫星姿态控制框图如图1所示,姿控系统的姿态控制采用PID控制和前馈干扰补偿控制的复合控制方法.

图1 姿态控制框图Fig.1 Block diagram of attitude control
PID控制器的PID控制律设计如下:

式中:Δφj和Δφj分别为姿态角和角速度误差;Tjc为PID控制力矩;Tsgj为式(1)的陀螺力矩,kpj、kij和kdj为PID控制参数.
一般而言,PID控制器的执行周期Δtc大于干扰补偿器需求的执行周期,由上述分析可知,考虑到前馈干扰补偿控制的实时性和有效性,要求每隔Δtp更新补偿力矩,这样在执行完PID控制器的计算后,传递给执行机构的力矩指令为:
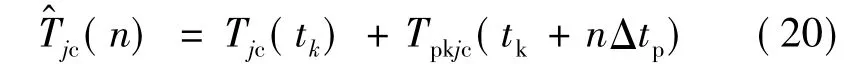
3 验证
某三轴稳定对地卫星具有一个转动载荷,载荷标称转速为 90(°)/s,卫星转动惯量为:Isxx= 520 kg·m2、Isyy=450 kg·m2、Iszz=660 kg·m2,轨道角速率ω0=0.001 1 rad/s.卫星采用动量轮进行三轴姿态控制,星敏感器和陀螺联合定姿,考虑部件安装系统偏差.设计轮控 PID控制器,带宽为0.02 Hz.姿态确定周期和Δtc均为0.25 s.
经分析,载荷干扰力矩曲线如图2所示,可见干扰力矩具有周期性,由式(14)估计得到卫星三轴姿态的稳态幅值分别为:0.001 2°、0.001°、0.001 1°.
卫星要求姿态稳定度优于0.000 5(°)/s,根据式(18)得到Δtp须满足0.016~0.084 s,设计干扰补偿控制器且取 Δtp=0.025 s.姿控系统时间5 500 s启动干扰补偿,补偿前后的卫星姿态角、姿态角速度、动量轮力矩变化等情况如图3~5所示,由图可见:
1)补偿前姿态角和姿态角速度均较大且为周期性变化,变化周期与载荷转动周期一致,最大姿态角速度约0.002(°)/s,三轴姿态的稳态幅值与估计的基本相同,说明式(14)正确;
2)补偿后姿态角和姿态角速度明显减小,虽然受估计的干扰模型误差等影响还有周期性残余误差,但是最大姿态角速度在0.000 2(°)/s内,姿态精度明显提高,且满足卫星姿态要求.
从以上仿真结果来看,本方法有效且有助于提高卫星姿态精度.

图2 转动载荷干扰力矩Fig.2 Rotatable payload disturbance torque

图3 干扰补偿前后的姿态角Fig.3 Attitude angles before and after disturbance compensation

图5 干扰补偿前后的动量轮力矩Fig.5 Wheels torque before and after disturbance compensation
4 结论
本文基于具有广义坐标形式的牛顿-欧拉方法建立了带有转动载荷和挠性附件的卫星姿态动力学模型和转动载荷力矩模型,研究了载荷产生的动不平衡力矩和静不平衡力矩的机理和特点.分析了载荷干扰对卫星姿态的影响特性.给出了卫星姿态控制系统设计干扰补偿控制器的条件和工程设计方法.验证结果表明,本文给出的方法有效,能够提高卫星姿态精度,而且姿态稳定度由0.002(°)/s提高到0.000 2(°)/s.
[1] 周勇,李正军,马超,等.海洋二号卫星大惯量旋转部件干扰力矩抑制技术[J].中国工程科学,2014,16 (3):43-49.ZHOU Y,LI Z J,MA C,et al.Reduced torque ripple for rotational load with high inertia of HY-2A satellite [J].Engineering Science,2014,16(3):43-49.
[2] BRIAN B,RICHARD G,SEARS A,et al.Rapid maneuvering of multi-body dynamic system with motion compensation[C]//AIAA/AAS Astrodynamics Specialist Conference.Washington,D.C.:AIAA,2014,4297:1-20.
[3] 吕利清,翁艺航,史耀强.微波成像仪扫描转动对卫星姿态的影响分析和控制实现[J].上海航天,2011,28(5):59-62.LV L Q,WENG Y H,SHI Y Q.Analysis on satellite attitude affected by microwave radiometer imager scanning and it’s control realization[J].Aerospace Shanghai,2011,28(5):59-62.
[4] 刘军,韩潮,张伟.星上转动部件对卫星姿态的影响分析及补偿控制[J].上海航天,2006,23(6):22-27.LU J,HAN C,ZHANG W.Analysis on disturbance of mobile bodies and compensation control of satellite attitude[J].Aerospace Shanghai,2006,23(6):22-27.
[5] 王佐伟,刘一武.基于干扰补偿的航天器直接自适应模糊控制[J].航天控制,2007,25(4):21-25.WANG Z W,LIU Y W.Direct adaptive fuzzy control for spacecraft attitude based on disturbance compensation[J].Aerospace Control,2007,25(4):21-25.
[6] 俞洁,廖瑛,刘伟.高精度遥感卫星力矩补偿技术[J].上海航天,2011,28(1):12-17.YU J,LIAO Y,LIU W.Torque compensation technology for high-accuracy remote satellite[J].Aerospace Shanghai,2011,28(1):12-17.
[7] 屠善澄.卫星姿态动力学与控制[M].北京:宇航出版社,2001.
[8] 胡寿松.自动控制原理[M].北京:科学出版社,2007.
On the Influence of Rotatable Payload and control for Satellite Attitude
WANG Xinmin1,2,CHU Yonghui1,2,ZHANG Junling1,2,YUAN Jun1
(1.Beijing Institute of Control Engineering,Beijing 100190,China; 2.Science and Technology on Space Intelligent Control Laboratory,Beijing 100190,China)
The attitude control of satellite with flexible appendage and rotatable payload is investigated.Attitude dynamics equations and rotatable payload torque model are presented on the basis of Newton-Euler method with generalized coordinates.The theory and characteristics on imbalance torque of rotatable payload are analyzed.Secondly,the influence of payload disturbance characteristics on attitude of satellite is studied,and the estimation method of attitude jitter is illustrated based on Laplace transform of transfer equation.Finally,the condition of a disturbance reduction controller is developed,which is applied to the satellite attitude control system,and the controller engineering application method is presented.The verification results show the effectiveness of the proposed approach,and the accuracy of satellite attitude is improved.
static imbalance;dynamic imbalance;rotatable payload;disturbance compensation
V448
A 文章编号:1674-1579(2016)05-0014-05
10.3969/j.issn.1674-1579.2016.05.003
王新民(1975—),男,高级工程师,研究方向为航天器导航、制导与控制;褚永辉(1983—),男,工程师,研究方向为航天器制导与仿真;张俊玲(1982—),女,工程师,研究方向为航天器控制与仿真;袁 军(1965—),男,研究员,研究方向为航天器制导、导航与控制.
*国家重大科技专项基金资助项目.
2016-02-29
