X线前臂骨折图像增强分析
2016-04-07刘成凤田敬北
刘成凤 田敬北

摘要:该文针对医学图像对比度差的特点,该文对前臂骨折图像进行了增强处理,采用灰度线性变换、锐化、小波变换三种方法进行了比较剖析,并应用均方偏差(MSE)与峰值信噪比(PSNR)对加强后的图像质量进行了评价。实验结果显示,应用小波变换的方法可以很好地保持图像的细节、边缘特点以及图像的清晰度。
关键词:前臂骨折图像;MSE;PSNR
中图分类号:TP391 文献标识码:A 文章编号:1009-3044(2016)03-0212-03
由于医疗设备等因素的影响,造成获得的图像由于存在失真和噪声而与实物存在不同程度的差异。尤其在利用现代数字图像处理方法对医学图像进行计算机辅助判断时,图像的质量显得更加重要,因此需先对图像进行预处理。一般而言,实现医学骨折图像的计算机辅助诊疗需要进行图像的预处理、分割、特征提取以及类别划分等步骤。
目前,适应于医学图像增强的方法较多,其中包括滤波、形态学处理、小波变换等,因此,需要找到适合于骨折图像的增强理论和方法来对骨折图像进行研究,使得处理后的图像能较好的保留边界和结构信息。本文以10幅前臂骨折图像做样本,均方偏差(MSE)与峰值信噪比(PSNR)作为处理之后图像的质量评定方法,对常用的图像增强方法的探讨比较剖析,结果显示采用小波变换的办法对骨折图像的加强效果最为显著,处理以后的图像骨骼以及背景部分的对比性显著加强[1-3]。
1 图像评价准则
通常,人的主观视角判定图像质量具有不精确性,所以,我们采用图像质量好坏的客观评定办法即均方误差(MSE)与峰值信噪比(PSNR)来评定图像质量的好坏。设[fi,ji=1, 2, …,N, j=1, 2, …, M]为原始图像,[fi,ji=1, 2, …,N, j=1, 2, …,M]为处理后的图像,[M,N]则代表骨折图像的长与宽,令[M=339,N=162,]则[fi,j]和[fi,j]两之间的均方误差定义(MSE)为:
均方误差体现的是原图像和经处置后图像间的差别,当值越低时,两图之间的差别越小,因此,均方误差越小的图像质量越好。
峰值信噪比(PSNR)定义为:
[fmax=255],[fmax]代表图像像素灰度值,其最大值为255,峰值性噪比则为取值越高,图像的质量也就越好。
2骨折图像增强方法
2.1 灰度线性变换
灰度的线性变换是针对图像内每一个像素点的灰度依照转换函数开展线性拓展转换。进而令对比度较低的图像层级更为丰富,同时优化视觉效果,起到加强图像的作用。设原图像为[fi,j],转换之后的图像为[fi,j],则转换函数的表达式为:
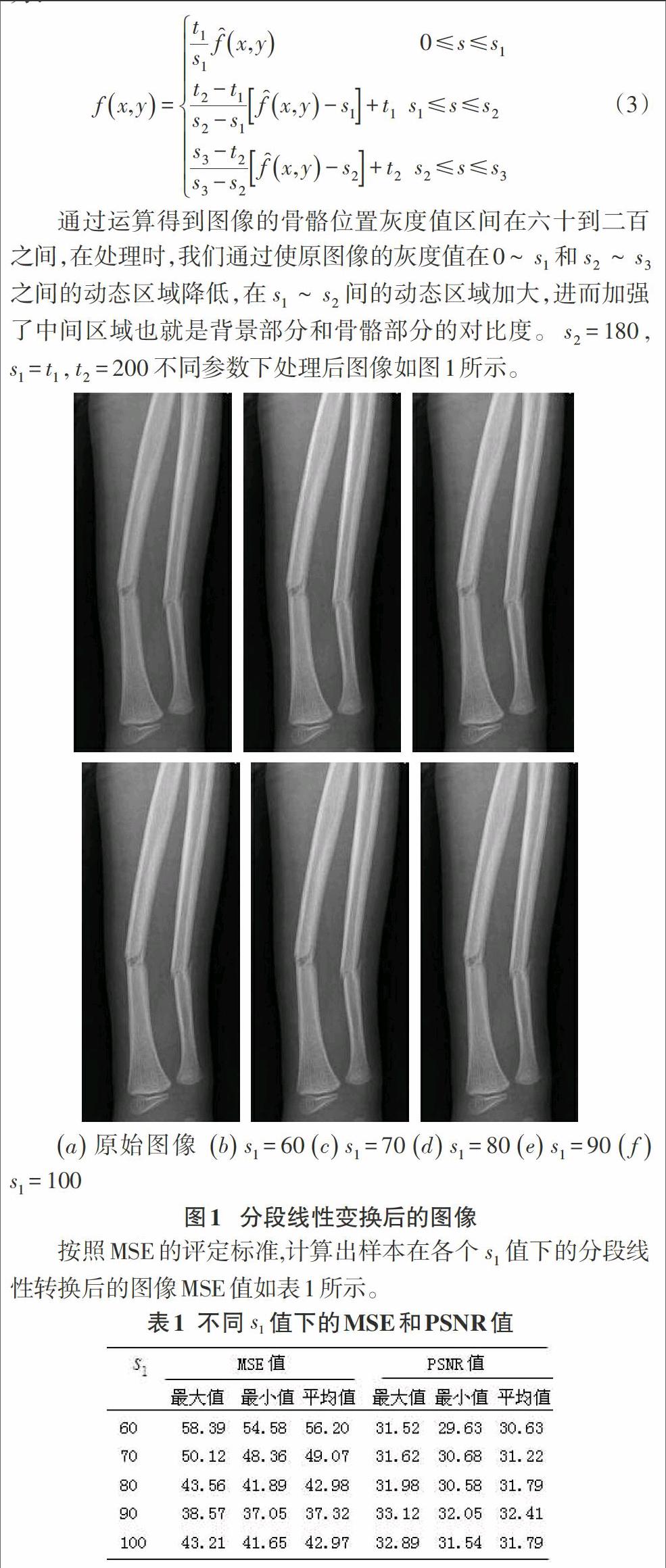
通过运算得到图像的骨骼位置灰度值区间在六十到二百之间,在处理时,我们通过使原图像的灰度值在0~[s1]和[s2]~[s3]之间的动态区域降低,在[s1]~[s2]间的动态区域加大,进而加强了中间区域也就是背景部分和骨骼部分的对比度。[s2=180],[s1=t1],[t2=200]不同参数下处理后图像如图1所示。
按照MSE的评定标准,计算出样本在各个[s1]值下的分段线性转换后的图像MSE值如表1所示。
结果表明随着[s1]值的增大,MSE值逐渐减小,PSNR值增大,骨骼区域对比度明显增强,[s1]值为90时MSE平均值最小,PSNR平均值最大,根据质量评价标准,此时增强效果最好。
2.2 锐化
锐化常常被用来加强图像轮廓部分的信息。它可以显著地凸显图像内的过渡区域以及模糊的细节。而算子不同对于图像的锐化成效各异,其中包含实现锐化的Laplace算子、sobel算子以及prewitt算子等[4]。
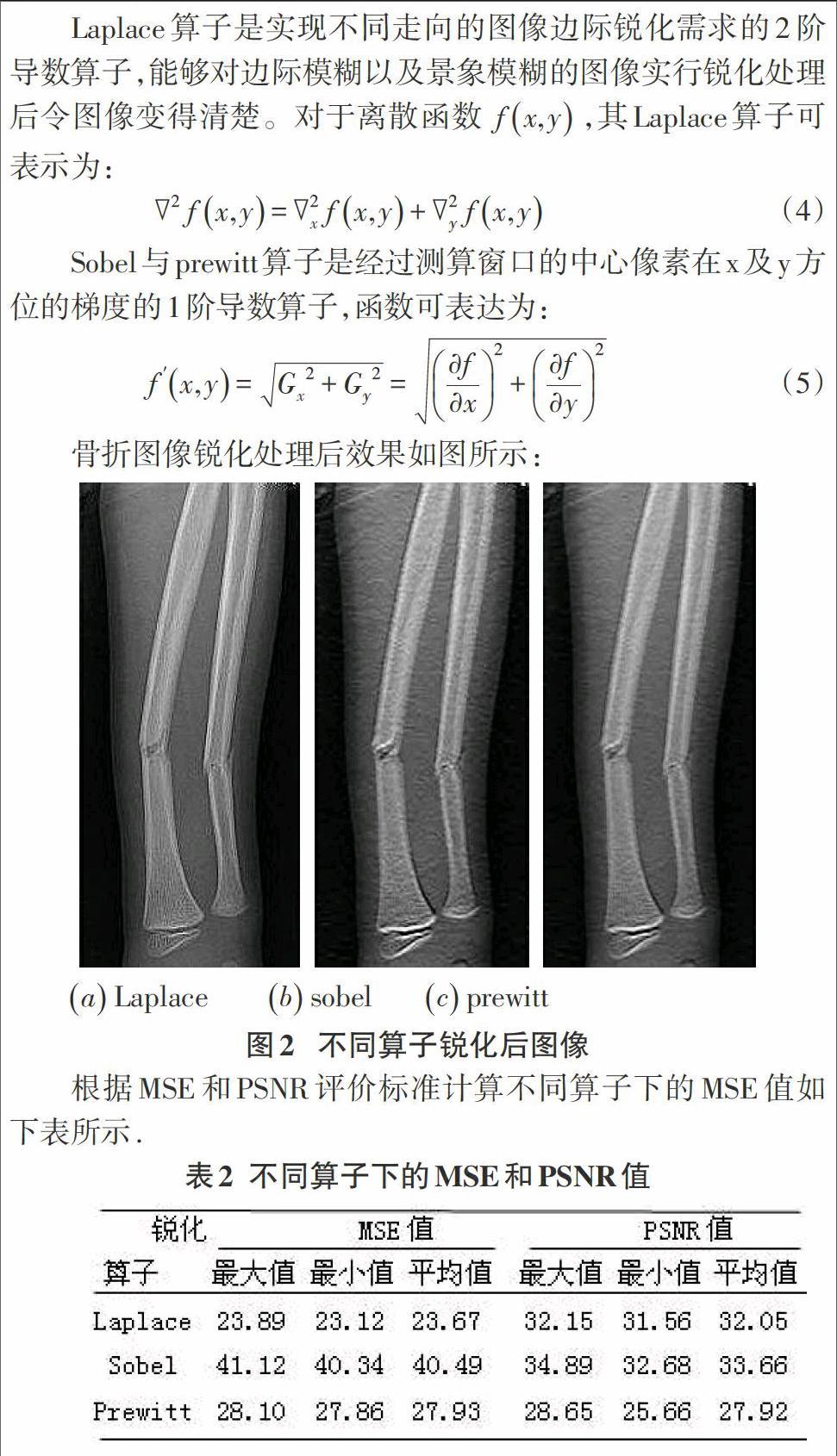
Laplace算子是实现不同走向的图像边际锐化需求的2阶导数算子,能够对边际模糊以及景象模糊的图像实行锐化处理后令图像变得清楚。对于离散函数[fx,y],其Laplace算子可表示为:
骨折图像锐化处理后效果如图所示:
根据MSE和PSNR评价标准计算不同算子下的MSE值如下表所示.
结果表明Laplace锐化后的图像MSE值最小且PSNR值最大,增强效果最好,较sobel和prewitt更好的突出了骨骼区域,且更好的保留了图像信息。
2.3小波变换
小波变换是经过伸缩与平移计算对原图像每一个像素点的信号逐渐展开多层次的细化以后获取的有效信息,而且能对其展开从构后达到图像加强。
2维形态下,小波变化的基本函数由2维尺度函数[?x,y]与小波[ψHx,y ][ψVx,y ][ψDx,y]就能够获得小波变换的基本函数:大小为[M×N]的图像[fx,y]的离散小波变换为:
小波的多层次分解中一级分解会出现水平、竖直和对角线3个细节分量以及1个低频分量,并且原图像会被平均分为四个频带图像,如图4所示,进行一级分解后的低频信息体现了图像骨骼部分的轮廓信息,高频信息则体现了各个方向的详细信息。二级分解时,再对低频分量展开二维离散小波转换,全部的子图像都通过原图像和2维尺度函数以及小波函数的内积在各个维度内完成基2的取样[5-9]。
经过两级分解后获得的两级分解之后各个方向的小波系数,再对图像展开单支重构,使其尺寸与原图像大小相同,并提升低频部分,从而提升骨骼轮廓,弱化细节。经小波变换后的图像轮廓清楚, 细节性信息被显著加强,对于总体较暗、对比度不佳的医用骨折图像拥有良好的加强效果,根据质量评价标准计算结果如表3所示。
3实验结果分析
本文以OpenCV 2.3.1作为平台,实验通过分别计算分段线性变换、锐化、小波变换三种常用方法处理后图像的均方偏差与峰值信噪比值,作为处理后图像质量好坏的评定标准,实验结果为:
实验结果表明小波变换的MSE值最小,锐化处理后的PSNR值最大,但由于锐化处理后的图像会出现不规则纹理,从而导致图像信息与原图像产生明显差异。小波变换通过多尺度的分解及重构后的图像质量较好,明显增强了骨骼区域,因此小波变换的方法较适用于该类骨折图像进行增强处理。
4 结束语
在骨折图像增强处理阶段,应根据处理的图像差异有针对性地选择算法,小波变换能有效提升骨折图像中骨骼部分和背景部分的对比度,使细节清楚,但分解及重构复杂。锐化增强效果根据质量评价标准也较理想,但需优化算法,在实际运用可结合实际需求,选择出最适合的增强方法[10]。
参考文献:
[1] 李云红.数字图像处理[M].北京:北京大学出版社,2012.
[2] 王蓉.图像增强算法实现[D].荆州:长江大学, 2013.
[3] 杨璐珍.医学图像增强处理方法的研究与实现[D].河南科技大学, 2011.
[4] 卢允伟.基于拉普拉斯算法的图像锐化算法研究和实现[J].电脑知识与技术,2009(6):1-3.
[5] 刘青青.基于二维离散小波变换的红外图像增强算法[J].计算机用于与软件,2006(11):1-3.
[6] 候艳芹.一种基于二维离散小波变换的医学图像增强算法[J].计算机工程与应用,2006(7):1-4.
[7] 卢剑.基于小波变换的图像增强算法[D]. 南京:南京理工大学,2013.
[8] 伊欣.基于小波变换的医学图像增强系统研究[D]. 西安:西安工程大学, 2012.
[9] 孟正中.基于小波变换的图像增强方法研究[D] .长沙:中南大学,2011.
[10] 沈晶.Visual C++数字图像处理典型案例详解[M].北京: 机械工业出版社,2012.
