基于遗传算法的物化视图选择优化

蒋国唯　王建军

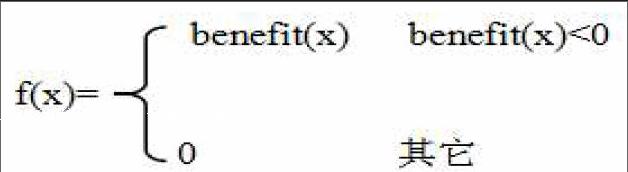
摘要：物化视图能够提高数据仓库的查询响应能力，但物化视图集的选择却很复杂。该文提出了一个如何选择物化视图集的优化遗传算法，在有限的存储空间下，使查询性能和视图维护代价较小。提出一个查询维护代价模型，并优化了交叉算子。实验结果表明，该算法在执行代价上优于经典的遗传算法。

关键词：遗传算法；物化视图；代价模型；交叉算子

中图分类号：TP18 文献标识码：A 文章编号：1009-3044（2016）03-0203-04

1 背景

数据仓库[1]是面向主题的、非易失的、能够反映历史变化的、集成的数据集合。近年来，数据仓库广泛应用于各行各业，并且数据量迅猛增长，查询响应所需时间也越来越长，查询优化成为数据仓库中的一个研究热点。查询优化主要包含索引优化和物化视图技术。

物化视图选择问题是数据仓库领域的研究热点之一。斯坦福大学的Harinarayan[2]在1996年最早提出物化视图选择问题，此后贪婪算法BPUS（Benefit Per Unit Space）成了经典的物化视图选择算法。该算法基于多维数据格，所得结果与最优解的收益比不低于0.63。Shukla A在1998年提出了PBS（Pick By Size）算法[3]，解决了贪婪算法在维度很高的情况下计算最大收益效率过低、计算量大的缺点。GIA（Greedy Interchange Algorithm）算法是斯坦福大学的Gupta提出的[4]，它基于AND-OR图。1997年J.Yang等人最先提出用遗传算法解决物化视图选择问题[5]，根据多视图处理计划（Multiple View Processing Plan，MVPP），通过合并可以“共享”的公共子视图得到最好的多视图处理计划，然后从多视图处理计划里选取视图物化。随后利用遗传算法解决物化视图选取问题成为热点研究问题[6]。类似地，Kirkpatrick[7]提出了基于模拟退火算法的视图选择算法，模拟退火算法是一种基于Monte Carlo迭代求解法的启发式随机搜索算法，常常用于多维数的物化视图选取问题中。但是，基于模拟算法的视图选择效果依赖于正确的参数选择，好的参数选择往往需要进行多次实际测试。

静态物化视图选择算法如上所述，另有动态物化视图选择算法。动态算法在查询过程中动态的对物化视图进行增删改操作，以满足尽可能多的查询需求，主要包括包括DynaMat算法、Chunk算法和Cache算法。

十几年以来，人们对物化视图选择问题进行了大量而深入的研究，在这方面的研究也比较活跃的有国内的国防科技大学、复旦大学以及香港科技大学等。国内的学者也提出了许多物化视图选择算法的改进算法。王宜贵建立了代价估算模型，以物化视图的存储代价和查询的时间开销作为衡量标准，改进了基于遗传算法的物化视图优化算法[8]。王自强、孙霞提出增强遗传算法[9]。赵秀丽提出蚁群算法[10]，采取对信息素的全局和局部更新，并局部搜索每次迭代的最优解。龚安提出蚁群-遗传算法[11]，利用遗传算法的较强全局搜索能力优化蚁群算法每次的搜索结果，并且在进行信息素更新时同时考虑最差路径和最优路径上的信息素，改进后的算法最优解的收敛速度提高了，解决了存在于蚁群算法中的“早熟”停滞现象。徐海涛提出了一种混合算法，混合算法结合了模拟退火算法和遗传算法的优点[12]，解决物化视图的选择效果很好。

数据仓库中的物化视图选择影响查询效率和OLAP分析质量，目前基于遗传算法的物化视图选择问题已成为重要的研究热点问题。

2 遗传算法

遗传算法基于达尔文的“自然选择，适者生存”原理，是一种模拟生物演化过程的搜索最优解算法[13]。遗传算法主要包括三个重要操作，即选择、交配和变异，从任意一个代表问题可能潜在的解集的初始种群出发，经过不断逐代演化最终进化到最适应环境的群体。遗传算法的主要几个步骤如下所述。

1）二进制编码。多维视图格模型中，一个视图格对应一个n位的基因编码，n是视图格的总节点个数。某一位的编码是0，那么该位对应的节点不必物化；若编码是1，该位对应的节点需要物化。比如视图格包含节点v1，v2…v8，如果基因编码为11000001，那么应该选择节点v1，v2，v8进行物化。

2）适应度函数。适应度一般是物化视图的收益值。定义如下适应度函数：

3）随机生成初始种群。初始化N个染色体。

4）各种遗传算法算子。选择算子设定为2个染色体中适应度较大者用于繁殖下一代。交叉算子设定为交换二进制编码交叉点之前的二进制位，交叉点后面的二进制位保持不变。变异算子操作是二进制编码的某一位或者某几位以一定概率取反。例如染色体11010100和染色体11101010，交叉操作在第4位得到11100100与11011010，变异操作在第2位则为10010100 与10101010。

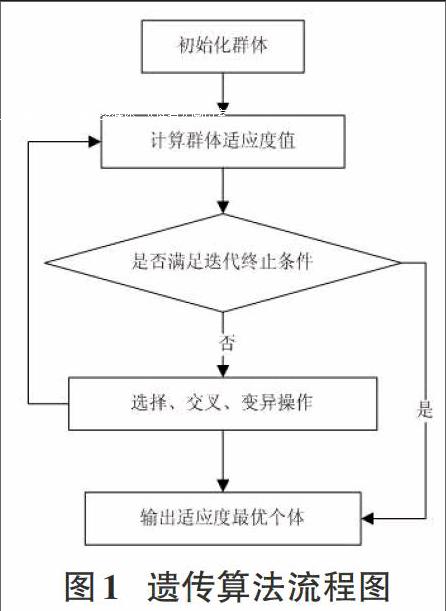
遗传算法的流程图如下图：

遗传算法的求解能力很强，并且它和最优解的收益比非常高，有着迅速的全局搜索能力，这优于蚁群算法的局部搜索能力强，遗传算法搜索结果也优于贪心算法等启发式算法。然而不当的遗传算子会导致遗传算法收敛速度很慢，而且随机性特点使得算法收敛慢，对算法的性能造成影响。

经典的GA算法在演化初期选择压力（最佳个体选中的概率与平均选中概率的比值）大，选中适应度高的个体，这些个体会控制演化过程，进而得出局部最优解，造成群体收敛早熟。在演化后期群体适应度值的差异较小，对应选择压力减小，收敛速度也降低很多。

针对上面描述的问题，本文提出了基于遗传算法的改进物化视图选择算法，我们通过新的代价模型、修改进化算子，用预处理算法生成初始解来对经典GA进行优化。

3 代价模型

物化视图的使用并不是万能的，也有其缺陷：

1）物化视图也要在数据库中存储，一定的存储空间占用也是必需的。

2）数据仓库不定期更新，新加入的数据在物化视图中没有存储，因此物化视图需要维护更新，必须要保持和基础数据表中的数据同步。

因此，哪些视图被物化是一个复杂的问题，需要按照查询的实际需求，并将存储代价、视图维护代价和查询代价三个因素全部纳入考虑范围，以选择需要物化的视图。本文提出了一种查询维护代价模型。

本文采用物化视图的线性代价模型。设与查询q相对应的视图是v，那么q的执行代价与v的元组数成正比。若物化视图v，那么v中的元组数就是q的查询代价；若没有物化v，且v的某个父视图被物化了，那么父视图中元组的个数便是q的执行代价；但如果v没有被物化，并且其父视图也不在物化视图集中，那么系统必须将事实表中的所有元组全部遍历来回答q，这种情况下事实表中所有元组的个数将等于q的执行代价。显然第一种情况下q的执行代价最小，q执行代价最大的是最后一种情况。

设数据仓库查询集为Q，Q={q1，q2，q3，...qn}，对应的视图集V={V1，V2，V3，...Vm}。Q（S）表示物化视图的查询代价，U（S）为维护时间代价，g为查询q的提交频率，h为视图V的更新频率。

定义1 查询总代价。当数据仓库中的物化视图集为V时，Q中全部查询的总代价是每个查询代价和该查询提交频率gi的乘积的总和。即

[Q（S）=i=1mgi*Q（qi，vi）]

定义2 维护总代价。当更新数据源表时，也要对应地修改物化视图，以保证数据一致性，修改物化视图的开销称为物化视图的维护代价。当数据仓库中的物化视图集为V时，视图集V的维护代价是每个视图的维护代价和更新频率hi的乘积的总和。即

[U（S）=i=1mhi*U（qi，vi）]

定义3 存储总代价，即为每个视图存储代价的总和，即

[M（S）=i=1mM（vi）]

定义4 查询维护代价模型。在一定存储空间rmax约束下，查询总代价和维护总代价之和Ttotal（S）为总代价。即

[Ttotal（S）=Q（S）+U（S）=i=1mgi*Q（qi，vi）+i=1mhi*U（qi，vi）] 式3-1

4 算法优化

4.1 初始解构造

遗传算法中，初始解非常重要，它决定着最优解的质量。可是初始种群随机产生是大多数的GA研究基础，随机产生需要很长的搜索时间，而且发现最优解的可能性还降低了。首先，预处理算法在物化视图集总存储代价M（S）

Begin

S=[φ]；

While （ M（S）

根据式3-1，对于S中的每个视图计算它的查询维护代价；

设C表示相对于S查询维护代价最小的视图；

If （M（S）+M（C）

S=S∪C；

End If

End while；

Return S；

End

4.2 编码

利用遗传算法寻优求解问题中，焦点问题是编码，编码在很大程度上影响着算法的性能，遗传操作方法和适应度函数的计算是根据编码方式改变的。常见的编码方式有格雷码编码、二进制编码、符号编码和十进制编码。目前遗传算法研究普遍采用二进制编码，所以本文也采用二进制编码。

多维数据格模型的格是一种有向无环图，例如在一个简单的借阅主题的数据仓库，该多维数据模型包括了3个维度Time，Book，Person以及一个Borrow Information事实表。那么OLAP 查询可能是关于时间与借阅者分组的借阅信息查询，也可能是按照借阅者分组与图书分组的借阅信息查询。3个维度有8种组合方式，记T，B，P代表3个维度，没有在分组条件中的记为All。视图间的依赖关系如图2所示，沿箭头方向可达的两个视图之间都存在依赖关系。

利用广度优先遍历将多维数据格中的节点进行遍历排序，图2节点遍历后的顺序是：（ALL，ALL，ALL），（T，ALL，ALL），（ALL，B，ALL），（ALL，ALL，P），（T，B，ALL）， （T，ALL，P），（ALL，B，P），（T，B，P）。

采用二进制编码，每一个节点只有两种状态，“1”表示对应的节点需要物化；“0”表示对应节点不物化。若节点对应的编码是00010001，那么第一个节点（ALL，ALL，ALL）对应二进制编码为0，代表对应的视图不需要物化，而第四个节点（ALL，ALL，P）对应的二进制编码为1，表示对应的视图应该被物化，其余节点依次类推。

4.3 适应度函数

在遗传算法演化过程中外部信息基本不被纳入考虑因素，仅考虑适应度函数（fitness function），搜索最优解是根据种群中每个个体的适应度值来进行的。个体在当前环境下的生存能力也是由个体的适应值决定。因此选取合适的适应度函数非常重要，好的适应度函数使遗传算法的收敛速度加快，进而找到最优解。概而论之，适应度函数是根据目标函数变换而来的。

物化视图选择问题可以描述为：在存储空间限制条件的情况下，寻找一个视图集V，使得"查询维护代价和最小"。所以算法的目标函数可以取这个代价和。很多研究把查询代价最小作为算法的目标函数，我们同时考虑了物化视图集的查询代价和维护代价，取目标函数为

[Ttotal（S）=Q（S）+U（S）=i=1mgi*Q（qi，vi）+i=1mhi*U（qi，vi）]

由于遗传算法的适应度函数通常设计成最大化，而视图选择的目标是查询代价和维护代价和最小，目标函数是最小问题。遗传算法要求，在优化过程中目标函数的变化方向应该和群体演化过程中适应度函数变化方向一致。因此考虑对目标函数作如下转换。

4.4 选择算子

选择是在计算比较群体中个体的适应度的基础上，选择适应度高的的个体，并淘汰适应度低的个体，然后把优化的个体直接遗传到下一代或者通过配对交叉产生新的个体再遗传到下一代。选择算子严格单调减少群体多样性，保证了遗传算法的“优胜劣汰，适者生存”的进化现象，遗传算法收敛的速率和效果在很大程度上取决于选择算子。

选择应该是动态的、全局的和自适应的，而不应是局限的。这样才能体现生物遗传融入环境因素的特征。提高计算效率、避免杰出基因缺失和提高全局收敛性是选择操作的主要目的。父代群体就是子代生存的社会环境，每个子代个体必然受整个社会形态影响——时代的影响，社会环境往往在个体生存过程中起着更为深刻广泛的作用。子代隶属于社会，而不仅属于父代。

基于上述思想，本文中采用一种混合策略的选择算子。首先，将最高适应度个体直接不作改变遗传到下一代，这样在进化过程中可以保证某一代的最优解不被交叉和变异操作所破坏，加快遗传算法的收敛过程。随后采取竞争法，即随机地选择两个个体，比较其适应度值，保留适应度值大的；若两个个体的适应度值相同，任意保留其中一个。重复此过程，直到配对库达到存储空间限制。竞争法保证了配对库中的个体有较好的分散性，同时又保证了加入配对库中的个体具有较大的适应值。

4.5 交叉算子

交叉是把两个父代个体的部分结构以一定概率Pc替换重组生成新个体的操作。交叉是遗传算法中起核心作用的操作，可以组合出新的个体。交叉是遗传算法区别于别的进化算法的重要特征。

经典遗传算法运用随机配对的方式、固定的交叉概率和传统的交叉算子进行配对，导致优秀基因有可能在遗传算法前期得不到保留，也会使遗传算法的收敛速度变慢；在演化后期，根据优胜劣汰原理，只保留了少量的优良的个体，这些个体往往具有相同或高度类似基因，近亲繁殖是无效的交叉操作，很难产生出新的个体，因此遗传算法不能跳出局部极值点，会呈现早熟现象。综上所述，本文提出改进的自适应交叉算法，根据适应度集中程度自适应调整种群的交叉概率。

其中，Pc0是初始交叉概率，fmax是个体适应度最大值，favg是个体适应度平均值，fmin是个体适应度最小值，f是两个个体中较大的适应度值。

该方法以最大适应度fmax、平均适应度favg和做小适应度fmin来衡量种群适应度的集中程度。favg/fmax>[α]且fmin/fmax>[δ]判断为种群集中。最初种群分散，Pc取初始交叉概率值，不会破坏种群的优良模式。经过多次遗传操作后，个体差异减小，满足条件favg/fmax>[α]，fmin/fmax>[δ]，Pc适当增大，可以使算法跳出局部极值。试验表明，改进的自适应交叉算子比传统的算法更容易避免局部收敛。

4.6 变异算子

变异模拟自然界生物体的基因突变现象，可以改变染色体的物理性状和结构。变异是一种局部随机搜索，能避免由交叉算子和选择算子引起的某些信息的永久性丢失，变异操作能够使遗传算法具有局部的随机搜索能力，保证遗传算法的有效性；变异操作可以保持遗传算法群体的多样性，有助于防止早熟收敛。

在遗传算法中，变异算子将所选个体某一位或某些位基因座上的基因值按变异概率Pm取反操作。对应当前个体的当前位生成一个伪随机数r，取值范围为[0，1]，若r小于Pm则将该位取反，否则保持不变。

通常变异概率Pm取值很小，位长、种群规模等因素都会影响Pm取值，一般情况Pm选取0.001～0.1（或取l/L，L是位串长度）。

4.7 改进算法步骤描述

经典遗传算法在编码方案中没有使用约束条件，考虑到数据仓库的存储空间有限，不能将所有的视图物化。因此改进算法中加入约束条件：有限的存储空间。算法描述如下。

Step1 按照4.1构造初始解；

Step2 计算最初群体中每个个体的适应度值；

Step3 确定下一代个体，具体操作按照4.4中的选择策略；

Step4 交叉操作，按照4.5中的交叉概率Pc进行；

Step5 变异操作，按照4.6中的变异概率Pm进行；

Step6 若视图存储容量达到rmax，则执行Step7，否则执行Step2；

Step7 将种群中最优适应度值的个体输出。

5 结束语

为了验证算法效果，我们对算法进行了试验。实验测试数据是某零售业销售记录组成的数据仓库，含有1个事实表和6个维表，其中共有候选视图28=256个，初始交叉概率Pc= 0.65，变异概率Pm= 0.06。我们对经典遗传算法和改进遗传算法的执行时间进行了比较。两种算法的执行结果如图3所示。

改进算法建立了代价估算模型，在有限的存储空间条件下，把物化视图的维护开销与查询开销的代价和作为衡量标准，并优化了交叉算子，实验证明该算法是有效可行的，并且执行代价比经典GA算法要小。

参考文献：

[1] Inmon W H. Building the Data Warehouse[M]. America： Wiley， 2005.

[2] Harinarayan V， Rajaraman A， Ullman J. Implementing data cubes efficiently[J]. in the Proceeding of SIGMOD， ACM Press， 1996： 205-216.

[3] Shukla A， Deshpande P M， Naughton J F. Materialized View Selection for Multidimensional Datasets[C]. Proceedings of the 24th VLDB Conference，New York， USA：ACM Press， 1998： 448-459.

[4] Gupta H， Harinarayan V， Rajaraman A. Index Selection for OLAP[C]// Gray A， Larson， Per-Ake. ICDE'97， Proceedings of the 13th International Conference on Data Engineering. Birmingham， UK： IEEE Computer Society Press， 1997： 189-255.

[5] Zhang C， Yang J. Genetic algorithm for materialized view selection in data warehouse environments[C]// Proceedings of the 8th International Conference on Data Warehousing and Knowledge Discovery， Florence： Springer-Verlag， 1999： 116-125.

[6] Homg J T， Chang Y J， Liu B J， Applying evolution algorithms to materialized vew selection in a data Warehouse[J]. Soft Computing， 2003， 7（23）： 574-581.

[7] Derakhshan R， Dehne F， Korm O， Stantic B. Simulated annealing for materialized view selection in data warehouse environments[M]//Hamza M H. Proc. of the 24th IASTED Intl Conf. on Database and Applications. Innsbruck： IASTED/ACTA Press， 2006： 8-94.

[8] 王宜贵. 数据仓库中查询优化研究[D]. 南京： 东南大学， 2006.

[9] 王自强， 孙霞， 张贤德. 数据仓库中用于视图选择的增强遗传算法[J]. 小型微型计算机系统， 2007， 28（2）： 367-371.

[10] 赵秀丽，数据仓库中物化视图选择问题的研究[D].天津：河北工业大学，2007.

[11] 龚安， 窦万蕊， 王彦. 基于蚁群-遗传算法的物化视图选取策略[J]. 微计算机应用， 2010， 31（1）： 16-20.

[12] 徐海涛， 郑宁. 数据仓库中物化视图选择的一种混合算法[J]. 计算机工程与设计， 2005， 26（10）： 2752-2755.

[13] 玄光男， 程润伟. 遗传算法与工程设计[M]. 汪定伟，译.北京： 科学出版社， 2000， 1.