考虑空间变异特性的边坡可靠度分析简化方法
2016-04-07董少亮朱营营
董少亮 李 辉 朱营营
(青建集团股份公司,山东青岛 266071)
考虑空间变异特性的边坡可靠度分析简化方法
董少亮李辉朱营营
(青建集团股份公司,山东青岛266071)
摘要:介绍了一种衡量边坡稳定性的简化处理方法,采用蒙特卡洛法与极限平衡法,对某均质边坡进行了可靠度分析,并将简化方法的结果与已有结果进行了对比,结果表明:失效概率误差控制在20%以内,可以尝试采用简化方法对边坡进行可靠度分析。关键词:边坡,可靠度,土体参数,空间变异性
0 引言
在过去的几十年里边坡稳定分析引起了相当多的关注。以往的边坡稳定确定性分析中,一般采用譬如Spencer法、Bishop法、Morgenstern-Price法、SARMA法、不平衡推力法等计算边坡的整体稳定性,该方法通常将同一个土层的土体参数看作是确定值,进而确定唯一的安全系数,所以确定性分析得到的安全系数并不能客观地反映边坡的真实安全程度[1-3]。随后人们又提出了可靠度分析方法,该方法以“可靠度指标”或者边坡“失效概率”来衡量边坡稳定性。一般采用矩方法、蒙特卡罗模拟等。其中蒙特卡洛法是一种依据统计抽样理论,利用计算机研究随机变量的数值计算方法,该法受问题条件限制的影响较小,应用越来越广泛,在目前是一种相对精确的方法[4-10]。然而,常规的可靠度分析中,通常将土层的参数值看作是符合一定分布规律的随机变量,土层内各点的参数是一致的,忽略了土体具有空间变异性这一重要特性,也即:没有考虑同一土层不同空间位置上土体参数的相关性和差异性。
为了分析土体参数的空间变异特性对边坡破坏概率的影响,本文提出一种简化的处理方法。该法根据土层的厚度与土体材料的相关长度的比值,将土层细化为一定数量的独立土层。本文拟利用蒙特卡洛法和极限平衡理论对某均质边坡进行系统可靠度分析,与已有结果进行对比分析,希望得到有益结论,对边坡可靠度分析的研究提供一定的参考。
1 考虑土体参数空间变异性的可靠度分析
1.1蒙特卡洛模拟
本文拟采用蒙特卡洛法[11]进行边坡可靠度分析,其中粘聚力和摩擦角c,φ是影响边坡稳定性的两个关键性指标。功能函数F为随机变量c,φ的函数[12]。即:

其中,Fs为安全系数,可以用Bishop法、Spencer法等计算得到。将随机生成的N个样本,依次代入功能函数F,可得到N个功能函数值,统计功能函数F<0的个数,记为M。那么边坡的失效概率大约为:

当N取值足够大时,得到的频率即可认为是边坡的失效概率,但在实际应用中,N通常取一大值,具体取值与要分析的失效概率成反比。
1.2土体参数空间变异性及简化方法
土体相关系数公式如下[13]:

其中,Rij为相关系数;zi-zj为土体中的两个点的距离;λ为相关长度。对于不同的土体有不同的相关长度,这个长度值就相当于土体中两点相关性的一个临界值,当土体中两点之间的距离小于这个临界值时,这两点之间的物理属性相关性较强;当土体中两点之间的距离大于这个临界值时,这两点之间的物理属性相关性较弱。
由式(3)可知,如果两点间的距离超过了相关长度,则两点间的相关系数就会急剧下降,近似地作为不相关处理;如果两点间的距离小于相关长度,则两点间的相关系数增大,两点高度相关。因此,我们根据土层的厚度与土体材料的相关长度的比值,将土层细化为一定数量得到独立土层,进而进行可靠度分析。
2 算例分析
该算例采用拉丁超立方抽样方法,随机抽取1 000个样本,利用Bishop法和Spencer法计算安全系数Fs。对每次抽样,均进行最小安全系数搜索,然后将安全系数Fs代入功能函数进行统计计算。其中Bishop法和Spencer法都选择正态分布、圆弧滑动面,
考虑文献[13]中的算例,该边坡为均质粘性边坡,边坡剖面图如图1所示,土体的密度为2 000 kg/m3,粘聚力c的均值为40 kPa,标准差为10 kPa,摩擦角为0°。

图1 算例边坡剖面图
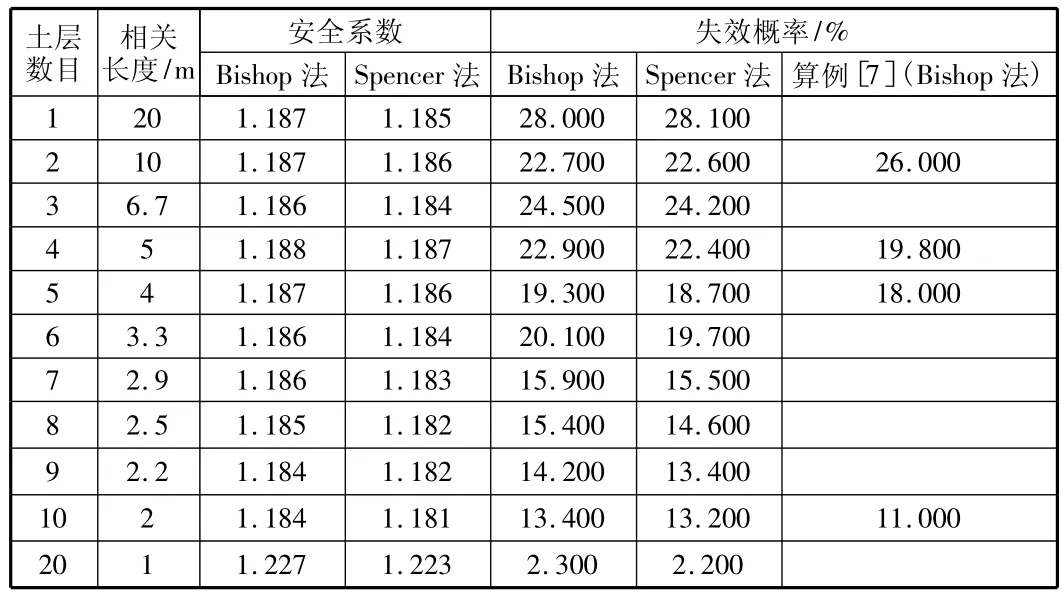
表1 计算结果汇总表
依次假定相关长度为1 m,2 m,2.2 m,2.5 m,2.9 m,3.3 m,4 m,5 m,6.7 m,10 m,20 m,相应的独立土层数目为20,10,9,8,7,6,5,4,3,2,1。用SLIDE软件模拟的结果如表1所示。
将本文用蒙特卡洛模拟在SLIDE软件中实现的简化方法结果与文献[13]中结果对比,如图2所示。
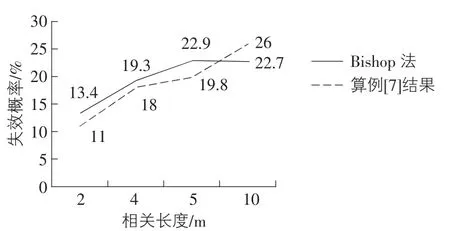
图2 失效概率折线图
本文简化方法结果与文献[13]中结果的相对误差如图3所示。
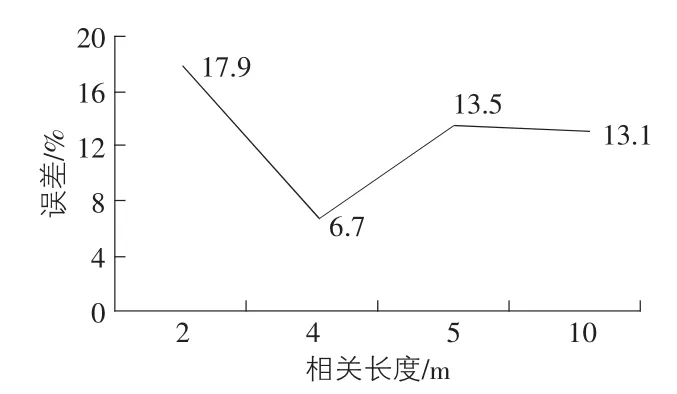
图3 失效概率误差图
由图3可以发现,本文简化方法结果与文献[13]随机场模拟的结果的相对误差控制在20%以内。
图4给出了不同相关长度下,系统可靠度分析需要考虑的滑动面的个数。

图4 滑动面个数
由图4可见,当相关长度较小时,需要考虑的危险滑动面个数较多,随着相关长度的增加,需要考虑的危险滑动面个数减少,这说明,当土体材料相关性较强时(相关长度较小时),系统可靠度分析需要考虑较多的危险滑动面,然而随着土体材料相关性的减弱(即相关长度变大),系统可靠度分析所需的危险滑动面较少,这与文献[8]中的结论一致。
3 结语
本文采用蒙特卡洛模拟方法,利用SLIDE软件,采用简化方法对某粘性土质边坡进行了考虑土体参数空间变异性的可靠度分析。结果表明:简化方法与文献[13]中算例相比,失效概率误差控制在20%以内,随着相关长度的增加,边坡系统可靠度分析中需要考虑的危险滑动面逐渐减少。简化方法可以尝试用于考虑土体参数空间变异性的边坡系统可靠度分析。
参考文献:
[1]熊赞民,高全臣,王春来.SLIDE在深基坑支护可靠性分析中的应用[J].矿业研究与开发,2008,28(2):39-41.
[2]任芳.基于蒙特卡洛法的边坡可靠度分析[J].福建建科科技,2010(6):13-14.
[3]祝玉学.边坡可靠性分析[M].北京:冶金工业出版社,1993.
[4]李亮,褚雪松,于广明.蒙特卡罗法在边坡失效概率计算中的应用[J].青岛理工大学学报,2012,33(6):6-9.
[5]吕惠,李亮,路世豹,等.土坡系统可靠度分析[J].山西建筑,2013,39(22):47-48.
[6]褚雪松,李亮,吕慧.考虑土体材料二维空间变异特性的边坡可靠度分析[J].水利水电科技进展,2015,35(2): 32-36.
[7]李亮,褚雪松,郑榕明.Rosenblueth法在边坡可靠度分析中的应用[J].水利水电科技进展(CSCD),2012,32(3):53-56.
[8]褚雪松,李亮.伪蒙特卡罗法及其在边坡可靠度分析中的应用[J].土木建筑与环境工程,2013,35(6):33-39.
[9]褚雪松,王旭春,张勇强,等.基于代表性滑动面的边坡系统可靠度分析[J].煤炭学报,2014,39(6):1077-1083.
[10]李亮,褚雪松,袁长丰.快速蒙特卡罗法及其在土坡可靠度分析中的应用[J].煤炭学报,2013,38(9):1576-1582.
[11]陈祖煜.土质边坡稳定分析——原理、方法、程序[M].北京:中国水利水电出版社,2010.
[12]杨继红,刘汉东,秦四清,等.考虑土性参数空间变异性的边坡可靠度分析[J].工程地质学报,2007,15(2):205-207.
[13]Wang Yu,Cao Zijun,Au Siu-Kui.Practical reliability analysis of slope stability by advanced Monto Carlo simulations in a spreadsheet[J].Canadian Geotechnical Journal,2011,48(1): 162-172.
Simplified approach to reliability analysis of a soil slope stability taking into consideration of spatial variability
Dong ShaoliangLi HuiZhu Yingying
(Qingjian Group Corporation Ltd,Qingdao 266071,China)
Abstract:Introduces the simplified treatment for slope stability,Monte-Carlo method and limit equilibrium method is used to perform the reliability analysis of homogeneous soil slope.The obtained results are compared with those from the existing results.The comparison shows that the simplified method can yield the result within 20%error,so the simplified method can be used for slope reliability analysis.
Key words:slope,reliability,soil parameters,spatial variability
作者简介:董少亮(1984-),男,工程师
收稿日期:2015-10-27
文章编号:1009-6825(2016)01-0079-02
中图分类号:TU413.62
文献标识码:A
