基于Stoner-Wohlfarth模型磁性纳米颗粒的磁化反转

2016-04-07韦文森杜安杜海峰

物理学进展 2016年1期

关键词：磁化磁性磁场

韦文森，杜安，杜海峰

1.中国科学院强磁场科学中心，合肥2300312.中国科学技术大学微尺度国家实验室，合肥2300263.东北大学物理学院，沈阳110819

基于Stoner-Wohlfarth模型磁性纳米颗粒的磁化反转

韦文森1,2，杜安3，杜海峰1∗

1.中国科学院强磁场科学中心，合肥230031
2.中国科学技术大学微尺度国家实验室，合肥230026
3.东北大学物理学院，沈阳110819

摘要：纳米磁性材料由于其特殊的磁学性能，近年来，在许多领域受到了广泛的应用。在基础理论研究中，人们提出了各种描述纳米磁性材料的理论；另一方面，计算机计算能力以及实验手段的提高，使得应用计算机进行材料设计以及探测单个纳米颗粒的磁学特性成为可能。这使得人们对纳米磁性材料的理解更加深入。本篇论文介绍了磁性纳米颗粒的磁化反转机制的基本理论与实验研究的最新进展。本文首先从磁性材料中基本的相互作用入手说明这些相互作用在纳米尺度下的表现形式，随后详细介绍了基于Stoner-Wohlfarth模型计算机模拟方法，最后简单介绍两种可以用来研究单个纳米颗粒磁化反转实验手段以及相关的实验结果。

关键词：磁性纳米颗粒；磁化反转；Stoner-Wohlfarth模型；Monte Carlo模拟；磁共振力显微镜；电子全息技术

*duhf@hmfl.ac.cn

I.引言

纳米科学技术是二十世纪80年代末诞生并正在蓬勃发展的一种高新技术。它的内容是在纳米尺度范围内认识和改造自然，通过直接操纵和安排原子、分子而创造新物质。它的出现标志着人类改造自然的能力已延伸到原子、分子水平，标志着人类进入了一个新时代—纳米科技时代。许多科学家预测，纳米科技必将成为21世纪的主导新技术之一。

纳米材料学是纳米科技的重要组成部分，它指的是：材料的组成相或晶粒结构控制在100 nm以下的长度尺寸的材料，分为两个层次，即纳米超微粒子与纳米固体材料。纳米超微粒子是指粒子尺寸为1～100 nm的颗粒；纳米固体是指由纳米超微粒子制成的固体材料，纳米材料由于其新奇的物理化学特性而成为科学研究的热点[1]。

纳米磁性材料是纳米材料的一个重要门类，由于纳米微粒的量子尺寸效应、小尺寸效应以及表面效应，使得它具有常规粗晶粒材料所不具备的磁特性，具体表现为超顺磁性、高矫顽力、高的各向异性参数、磁化率和传统不符等[2]。以纳米磁性颗粒为基本单位组成的纳米磁性材料，从一出现就表现出一些非常新颖的特性，因而受到科学家广泛的研究，获得了广泛的应用[3,4]。

II.基本概念以及研究进展[5]

A.纳米颗粒的磁性理论

在实际的纳米磁性材料中，存在着多种相互作用。这些相互作用对纳米磁性体系的磁学性质起着重要的作用，下面就常用的相互作用做一简单介绍。

1.磁性材料的基本相互作用

a.交换能

在铁磁性物质内部的某一小区域里，其所有的原子磁矩都朝一个方向排列，在没有外场的情况下，铁磁性物质也显示磁性，这种现象称之为自发磁化。为了解释铁磁性物质的特性，1907年外斯在顺磁性朗之万理论基础上，提出了“分子场”理论。“分子场”理论解释了磁性物质的特性，但对于“分子场”的起源，“分子场”理论并未解决。只有到量子力学建立以后，才真正解决了这个长期未获得解决的问题。1928年，弗伦克耳最先提出铁磁体内的自发磁化是起源于电子间的特殊相互作用，这种相互作用是电子自旋平行取向；与此同时，海森堡证明，分子场是量子力学交换作用的结果。根据海森堡理论，铁磁性物质中的处于晶体格点上两个最近邻的原子自旋Si与Sj存在交换相互作用，表述如下

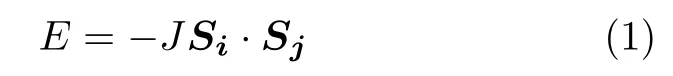
其中J称之为交换积分常数，在铁磁性物质中J为正值。从公式（1）可以看出交换能最小化要求最近邻的原子的自旋平行排列。在铁磁性的纳米磁性材料中，纳米颗粒为单畴，每个纳米颗粒有自己的自发磁矩，当两个纳米颗粒之间的距离小到一定程度时，它们波函数相互叠加引起纳米颗粒之间的相互作用能，一般表述为

其中µi和µj分别为波函数相互叠加的纳米颗粒的磁矩。

b.磁各向异性能

磁各向异性就是磁性物质在不同方向上有不同磁性的现象。主要表现为弱磁体的磁化率及铁磁体的磁化曲线随磁化方向的转变而变化。铁磁体的磁各向异性尤为突出，是铁磁体的基本磁性之一。磁各向异性按其起源的物理机制可以归纳为五类，磁晶各向异性、磁形状各向异性、磁应力各向异性、磁感生各向异性、交换磁各向异性。这里不具体探讨各种磁各向异性的物理机制，只简单介绍一下磁晶各向异性。温度低于居里温度的铁磁体受外磁场作用时，单位体积物质达到磁饱和所需的能量称为磁晶各项异性能，由于晶体的各向异性，沿不同方向磁化所需的磁晶能不同。对每种铁磁体都存在一个所需磁晶能最小和最大的方向，前者为易磁化方向，后者为难磁化方向。对于我们所研究的纳米磁性体系，单个纳米颗粒的磁各向异性能一般可表述如下

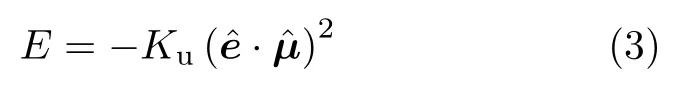
其中Ku为磁各向异性能常数，ˆe和ˆµ分别为纳米颗粒易磁化方向单位矢量和磁矩方向单位矢量。

c.塞曼能

任何磁体置于外磁场中，都将受到外磁场的作用，处在磁化状态下的磁体具有静磁能量，也叫做塞曼能。当铁磁体的磁化强度为µ时，在磁化强度为H的外场中，它们之间的相互作用能量密度为

对于单个纳米磁性颗粒，如果纳米颗粒的磁化强度为µ，处在磁化强度为H的外场中，颗粒的体积为V，则此单畴纳米颗粒和外场的相互作用能大小为−µ0Vµ·H。

d.退磁场能

有限尺寸的磁体，处在外磁场H中，被磁化后可能存在下面两个条件之一：（1）磁化强度的法向分量发生变化，即n·H≠＝0；（2）非均匀磁化，即divM≠＝0，其表面内将产生磁极，如图1所示。表面磁极是磁体内部存在与磁化强度M方向相反的一种磁场Hd，起着减退磁化的作用，故称为退磁场。式中比例系数N称为退磁因子张量，为无量纲的张量，同磁体的形状有关。要想获得该函数的具体形式是极困难的。只有当磁体的形状使Hd分布均匀时，N才变为常数。对于旋转椭圆体的三个主轴方向退磁因子之和，存在一个简单的关系Na＋Nb＋Nc＝1。

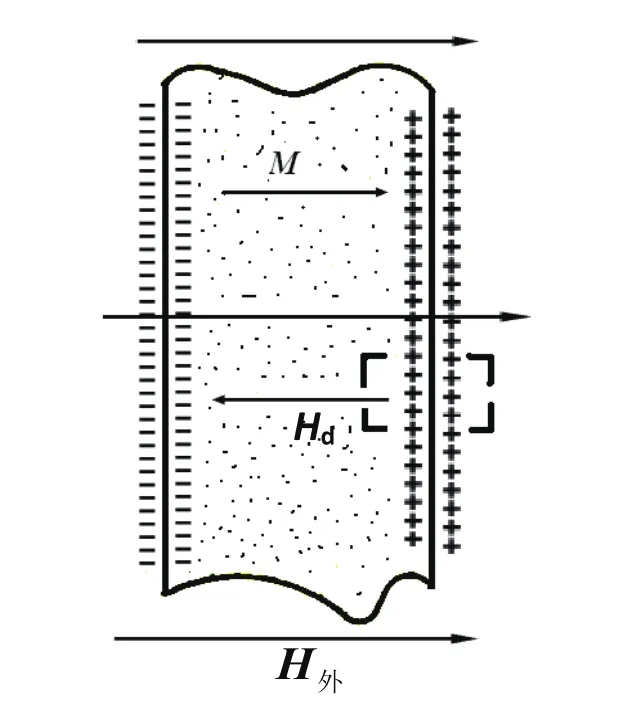
图1.退磁场形成示意图，摘自文献[4]

退磁场Hd的大小与磁体的形状及磁极的强度有关。若磁化均匀，则退磁场也是均匀的，且与磁化强度M成正比，即

磁体在其自身的退磁场中所具有的位能即为退磁场能。当磁体内部均匀一致时，退磁场能量密度为

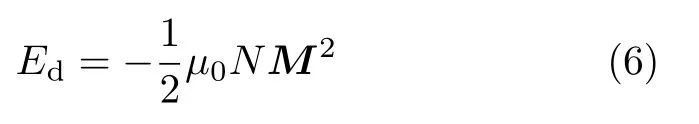
不同形状的磁体，沿不同方向磁化时，其相应的退磁场能量是不同的。这种因磁体的形状不同而引起其能量的各向异性称为形状各向异性。退磁场能量是一种形状各向异性能量。由于退磁场的存在，在测量铁磁性材料的磁化曲线时，通常将样品做成退磁场为零的环状形式，对于退磁场不为零的样品，测量后得出的表观磁化曲线，要进行退磁修正。在做纳米磁性薄膜型材料的模拟时候，退磁场是需要考虑一个因素。

e.偶极作用能

偶极子之间的相互作用能称之为偶极相互作用能。对于磁矩矢量分别为µi和µj的两个偶极子，它们之间的相互作用能可以通过先计算一个偶极子产生的磁场强度，然后计算另一个偶极子在前一个偶极子产生的磁场中静磁能得出。最终的结果为[15]

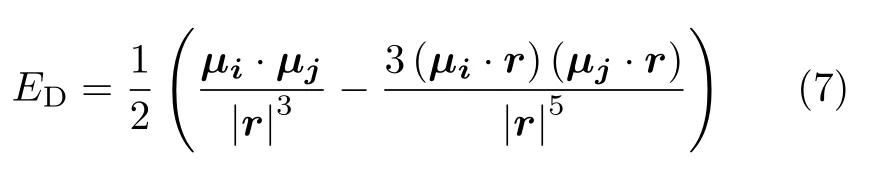
其中，r为连接两个偶极子中心的矢量。两个未接触的均匀磁化球之间的磁相互作用具有和两个偶极子之间的相互作用相同的形式[17]。

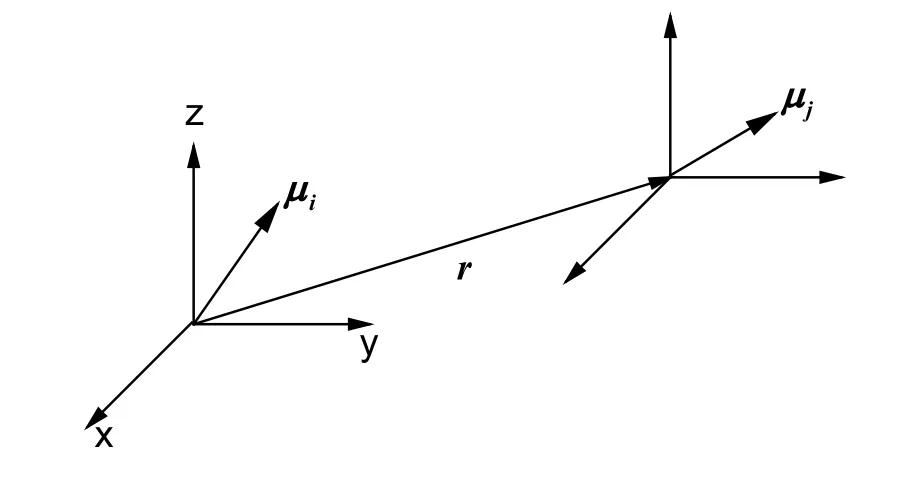
图2.偶极作用示意图

2.单畴临界尺寸[6−9]

纳米颗粒一般都为单畴结构，本节将说明纳米颗粒形成单磁畴的原因。前面分别讨论了铁磁体内的几种相互作用能量，即交换能、磁各向异性能、塞曼能、退磁场能和偶极作用能。根据热力学平衡原理，稳定的磁状态一定与铁磁体内的总自由能是极小时的状态相对应。铁磁体内产生磁畴，实质上是自发磁化平衡分布要满足能量最小原理的必然结果。假设铁磁体内无外场和外应力的作用，自发磁化的取向，应该由以交换能、磁晶各向异性能和退磁场能共同构成的总自由能为极小来决定。若交换能和磁晶各向异性能都同时满足最小值条件，则自发磁化方向只能在铁磁体的一个易磁化方向上。但是由于实际的铁磁体有一定的几何尺寸，自发磁化必然在铁磁体表面出现磁极而产生退磁场。这样就会因退磁场能的存在使铁磁体内的总能量增加，自发磁化的一致取向分布不再处于稳定状态。为了降低表面退磁场能，只能改变自发磁化分布状态。于是，在铁磁体内部分成许多大小和方向基本一致的自发磁化区域，这样的每一个小区域称为磁畴。对于不同的磁畴，其自发磁化强度的方向是各不相同的。因此，退磁场能最小要求是磁畴形成的根本原因。图3为单轴晶体内磁畴形成的示意图。但是，形成磁畴以后，两个相邻磁畴之间存在着约为103原子数量级宽度的、自发磁化强度由一个畴的方向改变到另一个畴的方向的过渡层。在这个过渡层内，磁矩遵循能量最小原理，按照一定规律逐渐改变方。，这种相邻磁畴之间的过渡层称为畴壁。磁畴壁内的各个磁矩取向不一致，必然增加交换能和磁晶各向异性能而构成磁畴壁能量。全面考虑，就不能单纯只考虑降低表面退磁场能而分成无限个磁畴，而是要根据退磁场能的降低和畴壁能量的增加的利弊，即由它们共同决定的能量极小条件来确定磁畴数目。

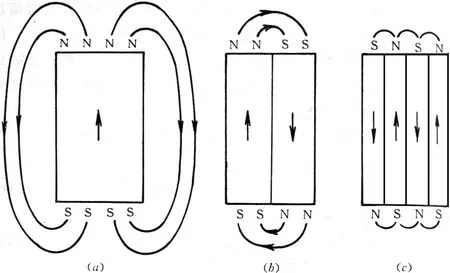
图3.磁畴形成过程，摘自文献[4]

在大块材料中，若不形成多畴，则退磁场能很高，所以大块材料多以多畴结构最稳定。因此一般讨论的多畴结构多数属于大块材料。若铁磁晶体材料的尺寸变得很小，不再是大块材料，成为多畴时的畴壁能比单畴的退磁场能还要高，这时候材料有可能不再分畴，只好形成单畴，具有更低的能量。如果铁磁晶体的尺寸足够小，近似于一个颗粒，自发磁化强度在一个方向上，成为一个稳定的单畴结构，这种颗粒称为单畴结构。单畴临界尺寸的计算需要用到微磁学原理，所谓微磁学原理就是指微粒中的磁化强度的分布和临界尺寸的大小应该根据自由能极小原理进行严格计算。纳米颗粒由于自身的小尺寸将形成一个单畴的结构，这为研究纳米磁性颗粒系统提供了一个方便。

3. Stoner-Wohlfarth模型

一般磁性材料磁滞现象出现有两种：不可逆畴壁位移磁化和不可逆畴转磁化。纳米磁性颗粒由于其单畴结构，没有畴壁，因此畴转磁化将是唯一的磁化机理。小颗粒系统的磁化过程一般用Stoner和Wohlfarth提出的一个模型来描述，简称SW模型。本节将详细的讨论此模型。

a. SW模型的提出

早在四十年代，Stoner和Wohlfarth就详细研究了单轴单畴微粒的转动磁化，建立了后来称之为SW模型的转动磁化机制[10,11]。由于我们假定所研究的纳米颗粒具有单轴单畴特性，因此SW模型就很自然的用于研究纳米颗粒系统的磁化行为。在SW模型中，取磁晶各向异性能Kusin2θ和磁势能−µ0MSH cos（α−θ）作为单轴单畴微粒的总自由能量密度E，即

式中Ku、MS、H分别为微粒的磁各向异性系数、饱和磁化强度和外磁场强度，α和θ分别是外场与易磁化方向的夹角和磁化强度与易磁化方向的夹角，用e表示易磁化轴方向，具体如图4所示。

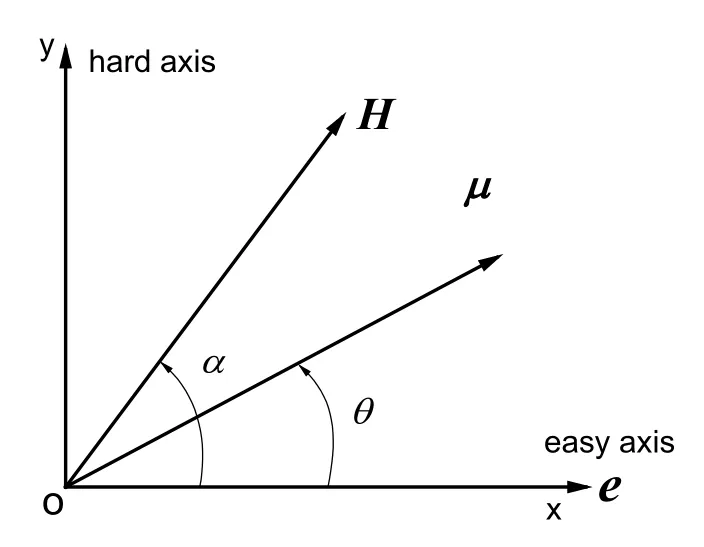
图4. Stoner-Wohlfarth（SW）模型，摘自文献[10]

式（8）也可变换为

式中h为约化场强的大小，h＝H/HK、HK＝2Ku/µ0MS。用一个新的变量ε＝E/Ku代表约化能量。当外场H与易磁化方向e一定时，颗粒的磁化方向µ将旋转到能量有极值的方向，因此需解如下的方程

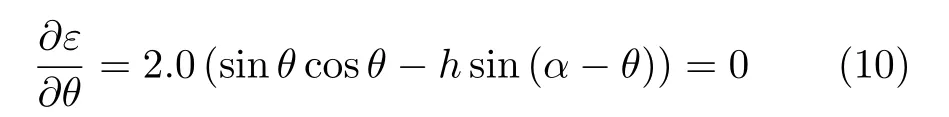
方程（10）为一超越方程，对此方程的研究发现：满足方程（10）的θ个数取决于h值的大小，存在一个临界转变场hc

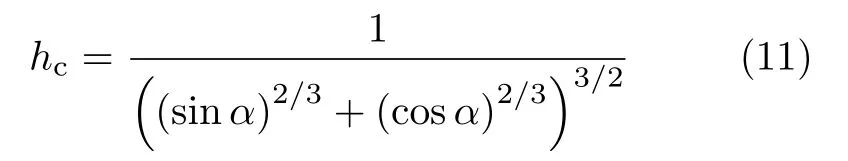
当|h|＞hc时∂ε/∂θ＝0有两个实数解，能量ε有一个极大值，一个极小值。当|h|＜hc时∂ε/∂θ＝0有四个实数解，能量ε有两个极大值，两个极小值。如图5所示

对于方程（10）引入约化磁场强度的两个分量hx＝hcosα、hy＝hsinα，方程（10）变为

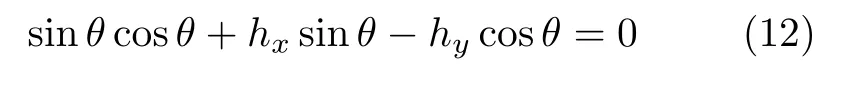
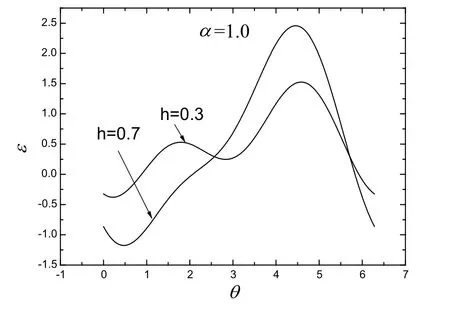
图5. SW模型中能量图

方程（12）不是所有的解都是稳定的，稳定的解要求∂2ε/∂θ2＞0，从稳定态到非稳定态的转变发生在∂2ε/∂θ2＝0，即

从方程（12）与方程（13）两个关于hx和hy的线形方程可得

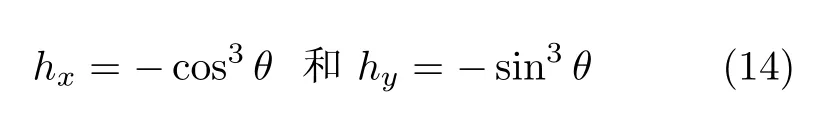
（14）式中消去θ，可得出hx和hy满足的关系

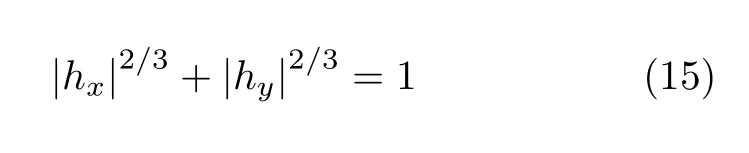
由曲线方程（15）可得出方程（11）。在hx−hy平面上满足方程（15）的曲线，称之为星形线，如图6所示。星形线上所有的点都满足∂θ/∂ε＝0和∂2θ/∂ε2＝0，方程（12）的图形解法可以在星形线上完成。方法如下：设OA表示约化后的外磁场方向，则满足方程（12）的平衡磁化方向平行于过A点并且和星形线相切的直线，如图6所示，平衡的磁化方向平行于BA和CA，此时有两个平衡的磁化方向。当外磁场变小，A点在星形线内部时，过A可以做出四条和星形线相切的直线，表示方程（12）有四个解，如图7所示。

图6. SW模型中星形线，两个解的情况。

图7. SW模型中星形线，四个解的情况

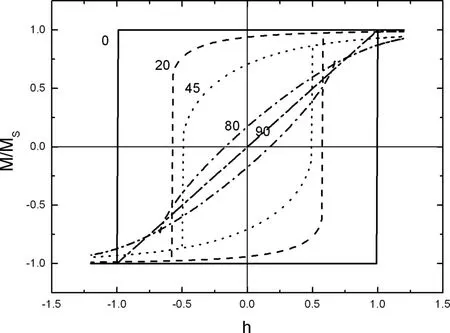
图8. SW模型中单畴磁化过程，摘自文献[8]

用星形线对方程（12）进行图解法求解，具有直观容易理解的特点，但没有给出解的数值形式，如果要求方程（12）的数值解，可用方程求根的数值解法（一般计算模拟中均采取的数值解法，我们将在下面给出解析求法）。

由SW模型，结合磁矩的一致旋转理论，可以计算出单畴小颗粒在无热扰动时的磁滞行为，这属于不可逆畴转磁化过程[4]。按着不可逆畴转磁化理论，SW模型中磁滞回线的形状依赖于外场与易磁化方向的夹角α。当α＝0时，磁滞回线为矩形，当α＝90度时磁滞回线变为直线，图8为各种不同的α值对应的磁滞回线。

b. SW模型的求解

在计算机模拟中，由于需要大量的解方程（12），出于节约时间考虑，用解析的方法求方程（12）的解是十分必要的，下面说明具体的求解过程。令

根据

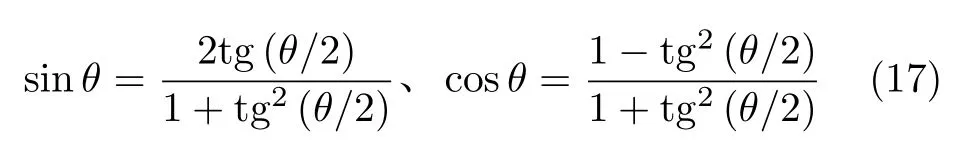
方程（12）可变为

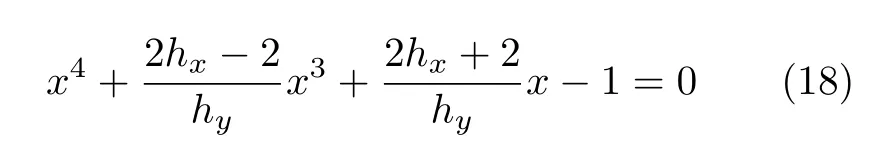
方程（18）可根据四次方程求解公式，进行数值求解,对于四次方程[12,13]

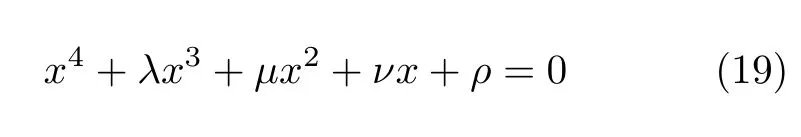
由四次方程的求解公式，式（19）和式（20）具有4个完全相同的根

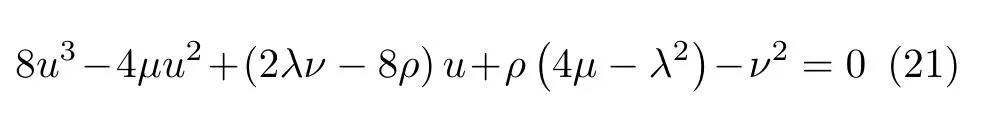
其中u是三次方程中的任一实根。由三次方程的求解公式，可取

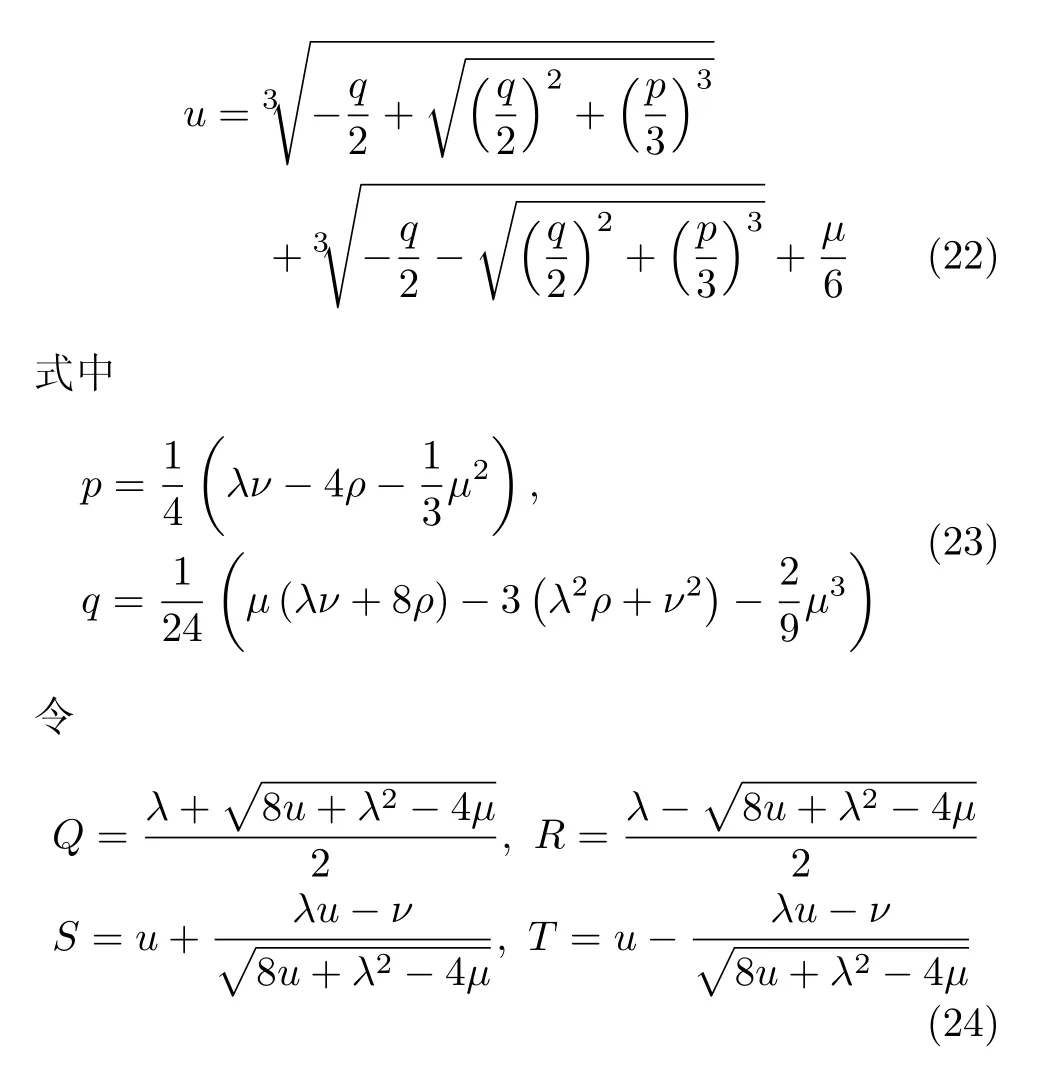
可得到上面两个二次方程的判别式D1和D2分别为

根据判别式最后可得到两个二次方程的实数解具有以下的形式：

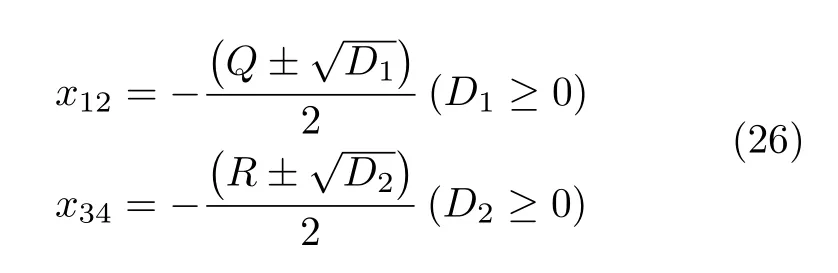
然后根据x＝tan（θ/2）得出能量极值对应的θ值。从上面分析可以看出在SW模型中假定外场H、颗粒的易磁化方向e和磁化方向µ在同一个平面内，因此上面的模型一个二维模型，即微粒的磁化方向只能在外场H与易磁化方向e所确定的平面内转动。

c. SW模型的三维扩展[14]

实际情况是颗粒的磁化方向可以在三维空间内任意转动，在此情况下，当颗粒之间没有相互作用时。单个微粒具有的总自由能量密度E一般表达式如下

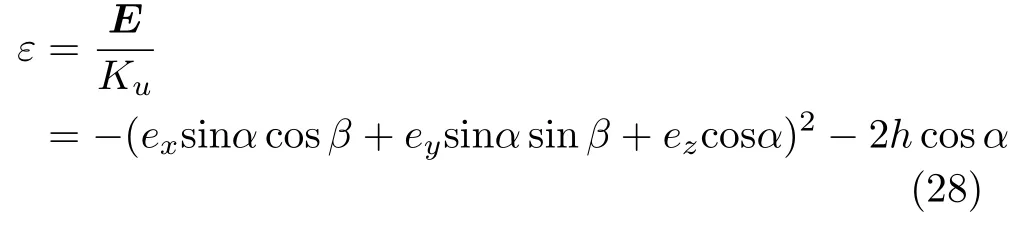
此时磁矩平衡的位置满足

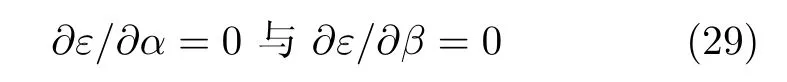
由∂ε/∂β＝0得（30）式或（31）式成立

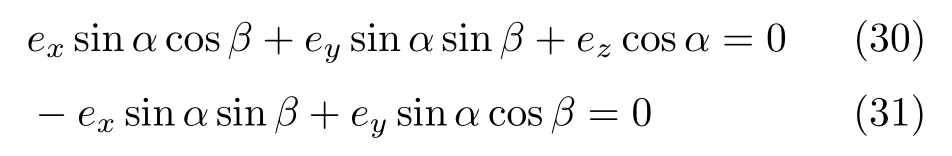
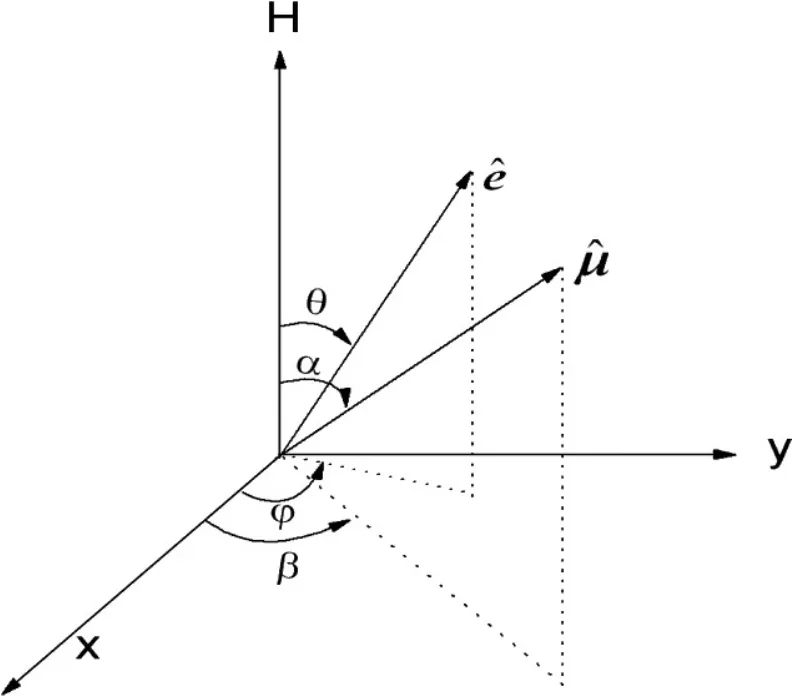
图9.三维SW模型示意图，摘自文献[14]

如果（30）式成立，再由∂ε/∂α＝0可得出sinα＝0，即ˆe与ˆµ相互垂直，且ˆµ在z轴方向或者−z方向，此时ˆe、ˆµ、H在同一个平面上。如果（31）式成立，也可得ˆe、ˆµ、H在同一个平面上。即由∂ε/∂β＝0可得ˆe、ˆµ、H在同一个平面上，如此把三维问题化为二维问题，然后可依照前节中的求解一元四次方程的方法解∂ε/∂α＝0。图10 和11是三维的SW模型的能量。

由（27）式描述的系统，根据上述分析，能量的极值情况和（12）式类似，也存在一个临界场hc，hc的大小‘（11）式给出，三维情况下和（11）中的α相对应的是β。在以后的模拟中当合外场小于临界场时，单个纳米磁性颗粒有两个能量极小值，如图11中的εmin1与εmin2，此时任意给定纳米磁性颗粒一个磁化矢量，如果此磁化矢量对应的能量小于εsad，需判定此磁化矢量所属能量区域，即此磁化矢量对应的能量所属能量区域。下面就给出判定依据。

图11.能量具有四个极值点的三维SW模型示意图，摘自文献[14]。

假设此时ε有两个极小值，对应的角坐标分别为（α1,β1）与（α2,β2），现任意取一个空间坐标（α′,β′），判断（α′,β′）所属于的能量区域。

图12.能量区域判定示意图

B.纳米颗粒的计算机模拟

本章简单介绍了计算机模拟方法，回答了以下问题：什么是计算机模拟方法，它有哪些优点？统计物理中蒙特卡罗算法的流程是什么？为什么要选择周期性边界条件以及如何选取？怎样产生空间均匀分布的单位矢量？

计算机模拟方法简介[15]

现代高新技术的发展，对材料的性能要求越来越高,由此对材料科学本身也提出了更高的要求。随着对材料微观结构与宏观性能关系了解的日益深入，人们将可以从理论上预言具有特定结构与功能的材料体系,设计出符合要求的新型材料，并通过先进工艺和技术制造出来，这种过程称之为材料设计。材料设计是人们所追求的长远目标，并非目前就能充分实现的。尽管如此，由于凝聚态物理学、量子化学等基础学科的深入发展，以及计算机能力的空前提高，使得材料研制过程中，理论与计算的作用越来越大，直至不可缺少。材料的计算机模拟是指依照相关理论，建立和所研究材料相对应的基本模型，借助计算机强大的能力，实现材料的设计。在计算机技术迅速发展的今天，计算机模拟已经成为解决材料科学中实际问题的重要组成部分。

计算机模拟技术的优势[16]

采用各种新颖算法的模拟技术，并结合运算功能强大的计算机，人们对物质内部状况进行德研究能够做到前所未有的细致和精确。这导致计算机模拟在材料科学中的应用越来越广泛，并由此产生了一门新的材料研究分支——计算材料科学。采用模拟技术进行材料研究的优势在于，它不但能够模拟各类实验过程,了解材料的内部微观性质及其宏观物理化学性能，而且还能在没有实际制备出这些新材料前就能预测它们的性能,为设计出优异性能的新型结构材料提供强有力的理论指导。材料科学研究中的模拟“实验”比实物实验更高效、经济、灵活,并且在实验很困难或不能进行的场合仍可进行模拟“实验”,特别是在对微观状态与过程的了解方面，模拟“实验”更有其独特性甚至有不可替代的作用。计算机模拟另一个用处是可以对理论方法无法处理的理论模型进行检验，计算机模拟已经成为自然科学中除理论、实验外的第三大分支，它们之间的关系如图13。计算机模拟领域中一个特别有实际意义的应用是生物学领域，在此领域人们正在从计算机创造出的虚拟空间中寻找真实世界的替身，完成实际情况下难于控制、代价高昂和对于社会及实验者自身过于危险的实验研究。

材料模拟方法与模拟层次

材料研究可针对三类不同的尺度范围[17]：（1）原子结构层次，主要是凝聚态物理学家和量子化学家处理这一微观尺度范围；（2）介观层次，即介于原子和宏观之间的中间尺度，在这一尺度范围主要是材料学家、冶金学家,陶瓷学家处理；（3）最后是宏观尺寸，此时大块材料的性能被用作制造过程，机械工程师、制造工程师等分别在这一尺度范围进行处理。既然材料性质的研究是在不同尺度层次上进行的，那么计算机模拟也可根据模拟对象的尺度范围而划分为若干层次，如表I.所示。在研究微观尺度下的材料性能时，统计力学仍是十分有用的原子级模拟方法。这种经典方法最明显的，就是对相变的理解。例如，固体的结晶有序,合金的成份有序或铁磁体的磁化。这种模拟属于所谓“物质的平衡态”，也就是物质从头至尾弛豫至与环境达到热平衡和化学平衡。但是,实际许多工艺上情况是远离平衡的,例如,在铸造、焊接、拉丝和施压等情况下,平衡统计力学是不合适的。最近十年期间，非平衡过程的理论和这些过程的数学建模技术已经取得很大进步。随着巨型计算机的出现，用于规则的结晶固体的模拟计算，已经达到了定量预测的能力。最新的进展表明有可能以相似的精度描述诸如缺陷附近的晶体形变、表面和晶粒边界的非规则图像。这些新方法甚至有可能用以研究物质的亚稳态或无序状态。

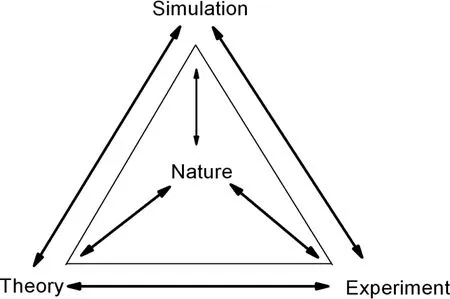
图13.计算机模拟、理论、实验三者关系示意图，摘自文献[19]。

表I.计算机的模拟层次、空间尺度及模拟对象

计算机模拟方法，按着空间的尺度可以分为以下几类[18]，如图14。

1.原子尺度模拟：所用的主要方法是分子动力学（Molecular Dynamics）和蒙特卡罗方法（Monte Carlo Simulation）。分子动力学方法是指，在单个原子的牛顿运动方程组合的基础上，根据给定的原子间相互作用力和外场，计算多粒子系统的结构和动力学过程。蒙特卡罗方法是用人工抽样实验来估计数值数学问题并求解的一种方法，它在计算系统的时间平均性质上比分子动力学方法更为有效。下面一节将详细介绍蒙特卡罗方法。

2.宏观尺度模拟：这是将材料看成连续介质，其宏观物理现象由代表质量、动量、能量平衡原理的偏微分方程所表述。对特定的材料则通过本构方程（constitutive equations）来反映。基于连续介质模型的模拟计算有两个根本出发点：一是要建立和反映材料宏观特性可测量之间的数学关系式，二是要运用材料的微观性质的知识，探索它们同宏观性质之间的联系。

3.介观尺度模拟：这是介于原子尺度和连续介质之间的模拟，也是目前发展的尚不成熟，困难最大的模拟。如何从原子尺度的模拟逐步推向连续介质模拟，或者反过来，如何从连续介质模拟逐步往下同介观尺度及原子尺度模拟联系起来，正是计算机模拟研究所要解决的问题。

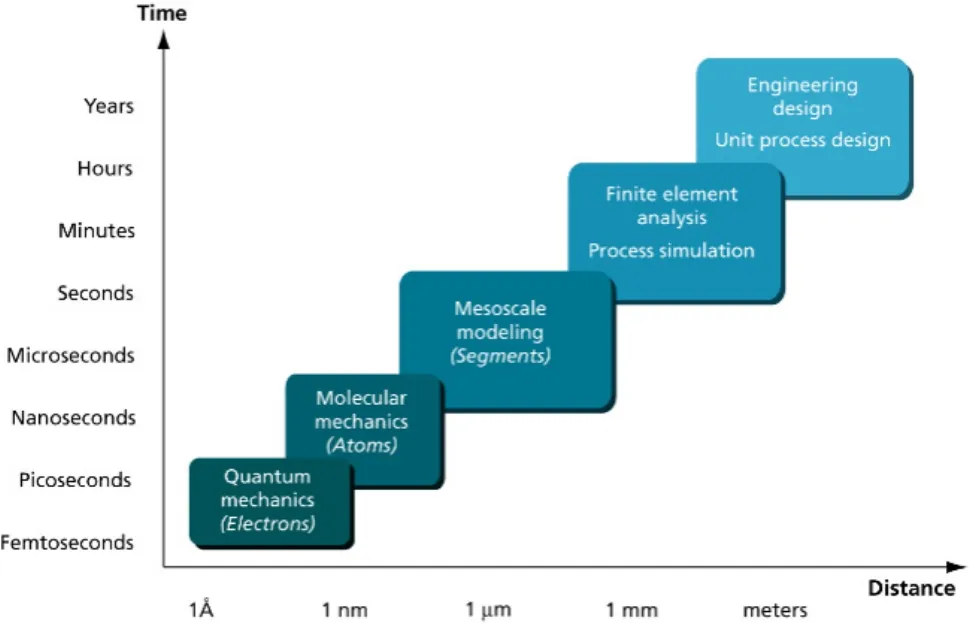
图14.计算机模拟理论方法、空间尺度及相应的时间尺度的关系，摘自文献[18]。

1. Monte Carlo方法简介

计算机模拟从采用的方法来看，它大致可以分为两种类型：

（1）随机模拟方法或统计实验方法，又称蒙特卡洛方法。它是通过不断产生随机数序列来模拟过程。自然界中有的过程本身就是随机的过程，物理现象中如粒子的衰变过程、粒子在介质中的输运过程等。当然蒙特卡洛方法也可以借助概率模型来解决不直接具有随机性的确定性问题。

（2）确定性模拟方法。它是通过数值求解一个个的粒子运动方程来模拟整个系统的行为，在统计物理中称为分子动力学方法。此外，近年来还发展了神经元网络方法和原胞自动机方法。

从蒙特卡洛模拟的应用来看，该类型的应用可以分为三种形式：

（1）直接蒙特卡洛模拟。它采用随机数序列来模拟复杂随机过程的效应。

（2）蒙特卡洛积分。这是利用随机数序列计算积分的方法。积分维数越高，该方法的积分效率就越高。

（3）Metropolis蒙特卡洛模拟。这种模拟是以所谓“马尔可夫”（Markov）链的形式产生系统的分布序列。该方法可以使我们能够研究经典和量子多粒子系统的问题。

a.统计力学中的Monte Carlo方法[19,20]

蒙特卡罗方法（MC）系统发展始于1944年，是乌拉姆和冯.诺依曼在其参加的曼哈顿研究工作时引入了的。它是这样一种方法：它使问题的解等于一个假设的统计模型的参数，用随机数列建立这个统计模型的一个样本，从它可以得出这个参数的统计估值。MC方法的应用范围广泛而且十分诱人，许多乍看之下不能用MC方法处理的问题，可以转化为随机性问题用MC方法处理。本论文所研究的纳米磁性颗粒体系可以归划为统计力学中的问题。基于此，这里只讨论MC方法在统计力学问题中的应用。

为了计算物理系统的特性，基本的做法是用基本的运动方程在相空间中生成一条路径，然后沿这条路径计算感兴趣的物理量的值。但计算物理中的MC方法采用的是不同的做法。它首先将系统用一个哈密顿量描述，并选择一个对问题合适的系综。然后用同这个系综相联系的分布函数和配分函数，就可以计算所有的可观察量了。MC方法的基本思想是，对主要的贡献抽样以得到观察量的估值。

假设所要求解的统计力学基本问题表述如下：

设有N个粒子，同每一个粒子i相联系，有一组动力学变量Si，它代表粒子的自由度。集合（（S1）,...,（SN））描写相空间。令x表示相空间Ω中的一点，假设系统由一个哈密顿量H（x）描述。

我们要计算可观察量A,令f（·）代表一个适当的系综，则A可以由下式计算出来：

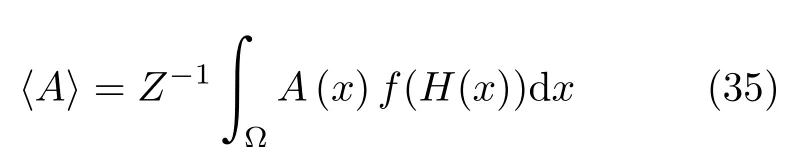
其中Z是配分函数

本论文所研究的磁学体系与外界没有能量交换，因此可以看成一个正则系综，对于正则系综的MC模拟，具体算法如下：

（1）规定一个初始位形

（2）产生一个新位形χ′

（3）计算能量变化∆H

（4）如果∆H＜0，接受新位形并回到第2步

（5）计算exp（−∆H/kBT）

（6）产生一个随机数R∈（0,1）

（7）若exp（−∆H/kBT）大于R，接受新位形并回到第2步

（8）否则，保留老位形作为新位形并回到第2步

最后去除一定的模拟步数，然后对以后的模拟量进行统计平均，即可得所要物理量值，上面的方法有时候也称之为Metropolis算法。

b.周期性边界条件

由于计算能力的限制，在计算机模拟中只能选取一定体积大小的对象进行模拟。所选取的模拟的对象即为元胞。为了将蒙特卡罗元胞从有限体积的模拟扩展到真实大系统，消除边界的影响，我们通常采用周期性边界条件（periodic boundary conditions）,如图15所示。采用这种边界条件,我们就可以消除引入元胞后的表面效应，构造出一个准无穷大的体积来更精确地代表宏观系统。实际上，这里我们做了一个假定，即让这个小体积元胞镶嵌在一个无穷大的大块物质之中。周期性边界条件的数学表示形式为其中A为任意的可观测量，n1,n2,n3为任意整数。这个边界条件就是令基本蒙特卡罗元胞完全等同地重复无穷多次。

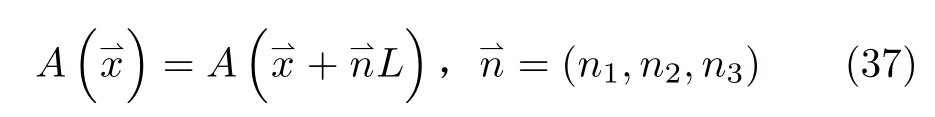
对于不同蒙特卡罗元胞盒子内粒子间的相互作用，如果相互作用是短程力，我们可以在rc长度处截断。这里V（rc）必须要足够小，以使截断不会显著地影响模拟结果。典型的蒙特卡罗元胞尺度L通常选得比rc大很多。我们往往选择元胞尺度rc满足不等式条件，使得距离大于rc的粒子间相互作用可以忽略，以避免有限尺寸效应。通常的数值应当选得很大使L/2＞rc。

在考虑粒子间的相互作用时，通常采用最小镜像力约定。最小镜像力约定是在由无穷重复的蒙特卡罗基本元胞中，每一个粒子只同它所在的基本元胞内的另外N−1个中（设在此元胞内有N个粒子）的每个粒子或其最邻近的影像粒子发生相互作用。

图15.二维周期性边界条件示意图

蒙特卡罗模拟的最小镜像力约定描述如下：

如图15所示，其中一个粒子通过图上虚线连线，与它所在元胞内的其它粒子或其影像粒子相互作用。处的粒子i同处的粒子j之间的距离为

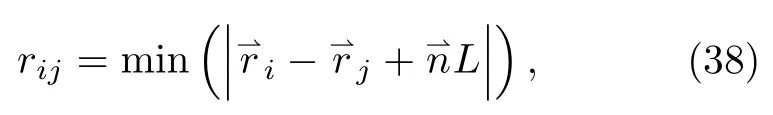
实际上这个约定就是通过满足不等式条件L/2＞rc来截断位势。采用最小镜像力约定会给模拟计算带来误差。

c.蒙特卡罗方法中的随机数

如上节所述，在使用MC方法中，要大量的使用随机数。MC方法模拟所得的结果一部分取决于随机数的质量，在此不详细讨论随机数的随机性对模拟结果的影响。有多种在计算机上产生随机数的方法。许多方法可以在文献[7]和[8]中查到[21,22]。计算机最常用的是[0,1]区间上均匀分布的随机数，最常用的方法是同余法，然后通过混洗（shuffling）操作来改善随机数的质量[23]。由均匀分布的随机数列到其它分布的随机数列有一定的变化规则[10]，这里也不做讨论。在我们所研究的系统中，最常用的是产生一个空间随机分布的单位矢量。在文献[20]中（145页）有详细论述[20]，不过我们采用的不是文献[20]所述，采取的变化如下：

空间随机分布的单位矢量相当于在单位球球面通过一定的方法产生一些均匀分布的点。根据高等数学知识，空间曲面的参数方程可以表示为[24]

在此参数方程下，空间曲面可以表示为

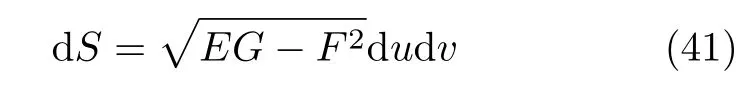
对于单位球面，按上面的规则如果采用球坐标系的α∈（0,π）,β∈（0,2π）来表示。根据式（39）到式（41），可得出单位球球面的面积元为

（42）式可写为

又因为z＝−cosα，因此如果采用z,β参数来描述单位球面，则

由式（44）很容易得出，如果参数z,β均匀分布，则它们产生的点在单位球球面上也将均匀分布。

2.纳米颗粒系统中常用的Monte Carlo方法

自从SW模型一出现，就引起了科学家的广泛兴趣，各种以SW模型为基础的理论与实验应接不暇。科学家的共同努力使SW模型对实际材料的描述也获得了很大的成功，本节主要说明一些基于SW模型常用的模拟方法以及它们的优缺点。

a.磁弛豫

考虑单个纳米磁性颗粒热扰动，当SW模型存在两个稳定态并且纳米磁性颗粒的初始磁矩位于一个稳定的能量区域中，由于热扰动，此纳米磁性颗粒从其初始的稳定能量区域跳出需穿越能垒∆E，根据N´eel等人的弛豫定律[25−27]

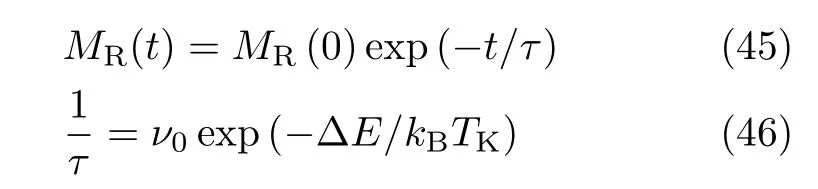
式中MR（0）与MR（t）分别代表系统初始时刻与t时刻的磁化强度，如果外场为零，则式中MR（0）与MR（t）分别代表系统初始时刻与t时刻的剩磁。v0一般为10−9～10−13，∆E为磁矩反转要克服的能垒，kB是Boltzmann常数，TK为系统绝对温度。对于无相互作用的大量处于相同状态的纳米颗粒集合，（45）式又可写为

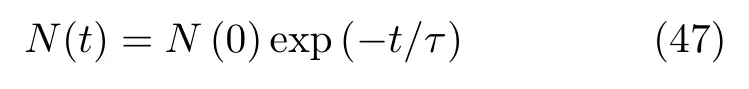
式中N（t）表示到t时刻发生磁矩反转的纳米磁性颗粒的个数。

根据N´eel弛豫定律，假设纳米磁性颗粒的易磁化方向沿z轴方向且没有外场，此时根据（46）式，可得出∆E＝KV，由此可定义冻结温度TB（blocking temperature），超顺磁性（supermagnetism）等相关的物理量。

b. SW模型常用的Monte Carlo方法

对于SW模型描述的磁性颗粒，如果采用标准MC方法，即Metropolis算法，由于Metropolis算法得出的是系统的平衡态性质，因此得不到磁滞回线，这和实际情况不相符合，因为实验对由纳米磁性颗粒组成的系统测量表明此类系统在有限的测量时间和一定的温度内总有磁滞回线。标准的Metropolis没有考虑颗粒的初始状态，也没有考虑颗粒磁矩转动的路径，因此导致在模拟SW模型时不适用。鉴于此，许多修正的适用于SW模型的MC方法相继提出。归纳起来主要有三种。

（一）局部MC方法（Local MC）[28−31]

在标准的MC方法中，设某个纳米磁性颗粒的初始磁矩方向的单位矢量为在随后的MCS中将产生一个空间方向随机分布的磁矩方向的单位矢量为是按前面说明的方法的随机产生，它和无关。而在局部MC方法中，选取和相联系，先在单位球球面上选取对应的点为圆心，画一个半径为δrmax的圆，在单位球球面上圈定一个范围，通过随机的在此范围内选取一个点代表的矢量来获得。采用这种算法，假如系统存在一个亚稳态，由于磁矩只在一个小范围做热扰动，因此在一定程度上能保证探求系统的亚稳态，对SW模型，可得到磁滞回线，这种方法的另一个应用是解决模拟系统低温时在相空间运动慢的问题[6]。但此种方法，有两点不容易确定，第一：δrmax的选取；第二：假如模拟的对象是纳米小颗粒，并且此小颗粒的几个稳定态对应的能量区域靠的很近，即使稳定态之间的能垒很高，采用这种的方法也很容易从一个稳定态跳到另一个和它靠的非常近的稳定态。

（二）两态模型（two-state model）[32−36]

两态模型就是根据N´eel弛豫定律，对每个纳米磁性颗粒定义一个冻结温度TB，当系统的温度低于TB时，纳米磁性颗粒只能停留在两个稳定态中的一个，然后通过解主方程或者直接求解能量极值获得在两个态之间反转的概率P12与P21；而当系统的温度高于TB时，采用标准的MC方法。为了考虑温度低于TB时颗粒热扰动，Jalil在稳定态的周围选取4个离散态作为可取的态。此种方法的一个缺点是没有完全考虑磁性颗粒在低温时候的热扰动，并且离散化会导致不确定的后果。

（三）三维SW模型[14,37]

在原有的模拟SW模型的MC基础上，考虑低温时，单个纳米小颗粒的热扰动，对上述选用的方法做一个改进。当约化后的合外场大于临界场时，采用标准的MC方法；当约化后的合外场小于临界场时，见图10～12,看纳米磁性颗粒所处的能量区域，如果一个纳米磁性颗粒初始的能量εI＜εsad，即此纳米磁性颗粒处于某一能量极小值附近区域，而后此纳米磁性颗粒随机产生一个的新方向。假设此随机产生的磁矩对应的能量为εL，如果εL＜εsad，则说明εL也属于某一能量极小值附近区域。如果此纳米磁性颗粒的初始能量εI与εL属于同一个极小值区域，则采用标准的MC方法；如果εI与εL不属于同一个极小值区域，磁矩转动至少要跨越的能垒εsad−εI，此时反转概率为exp（−KuV0（εsad−εI）/kBT）, T为系统的绝对温度，如果εI与εL有一个比εsad大，则磁矩转动不需要跨越能垒，这时采取标准的MC方法。

3.典型模拟结果[14,37]

a.系统在磁各向异性场作用下的磁化行为

在研究系统的整体行为之前，先研究单个粒子的磁学特性。

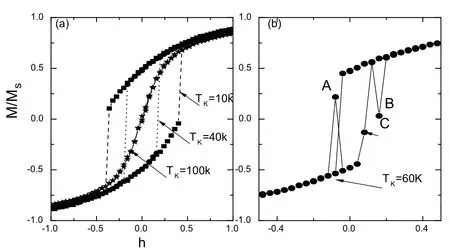
图16.单个颗粒的在不同温度下的磁滞回线，摘自文献[14]。

图16（a）和（b）为易磁化方向固定的单磁性颗粒在不同温度下的磁化曲线，随着温度的升高磁滞回线变窄直到消失，值得注意的是（b）模拟的A、B、C点有反常跳跃行为。为了探求出现这种行为的原因，我们做出了C点具体弛豫过程。如图17所示，刚开始时候磁性颗粒在一个能量极小的区域进行热扰动，随着MCS的增加，颗粒从一个能量极小区域转变到另一个区域，然后停留在此区域进行热扰动，总体的平均效果导致图16（b）中点跳跃现象。这样转变温度越低，需要的MCS越多，因此在100000 MCS条件下，温度为低温时颗粒没有出现这种跳跃现象。

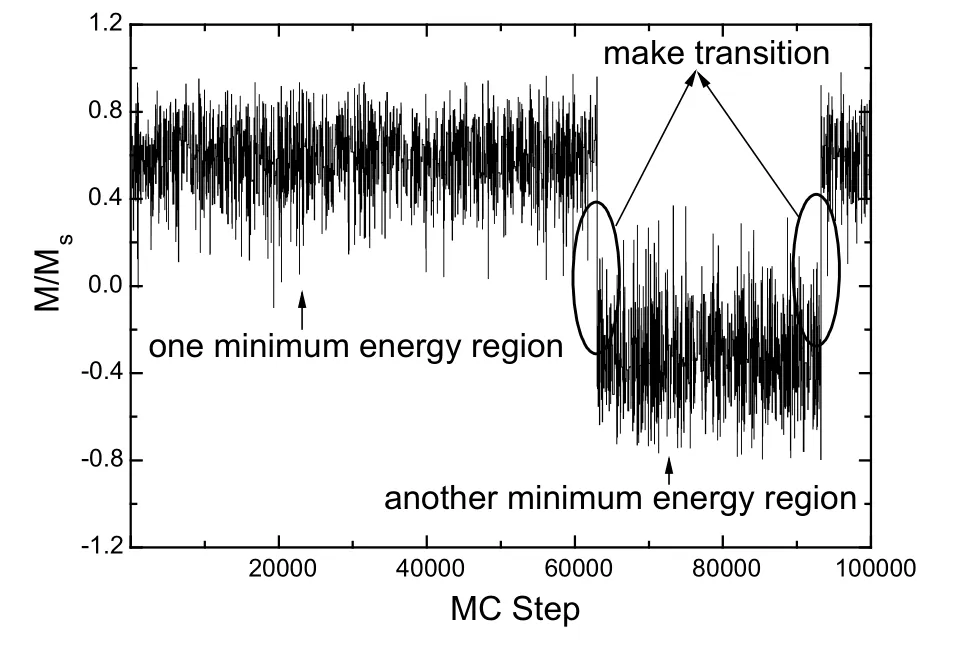
图17.图16（b）中C点的驰豫过程，摘自文献[14]。

图18为整个系统总体的磁滞回线，由于此时颗粒之间没有相互作用，因此我们考虑了两种粒径分布：（a）为均匀分布，（b）为对数正态分布（假若颗粒之间存在相互作用，此时不同颗粒之间波函数重叠的程度不一样，因此不能把不同颗粒之间的交换积分看成一个常数。当系统无序时，交换积分也不能看成常数，因此只对颗粒之间没有相互作用的颗粒系统考虑两种不同的分布，对本章以后所研究的非纯磁各向异性常的系统，颗粒的粒径完全相同）。相对于Xu的方法[34]，我们的方法在更广泛的温度范围获得了磁滞回线。图18（a）中，观察TK＝10 K的磁化曲线，OA段对应于颗粒的可逆的畴转过程，然后随着外磁场的增加，发生不可逆的畴转过程。低温时系统的剩磁为0.5，这和不考虑热扰动的SW模型的理论结果一致[38]。比较图18中的（a）与（b），发现粒径分布对数指数分布的系统磁滞现象出现的温度区域比粒径分布相同的系统广，对于粒径符合对数指数分布的系统，当T＝100 K时候，系统仍然有磁滞现象。出现这种现象的原因在于大粒径的颗粒具有高的磁滞温度区域，这些大粒径的颗粒的存在使得整个系统的磁滞温度区域变广。

图18.不同温度不同粒径分布的整个系统的磁化曲线，摘自文献[14]。

图19表示用Metropolis算法模拟出的系统的磁化曲线。模拟结果显示采用Metropolis算法模拟颗粒间无相互作用的系统得不到系统的磁滞现象。系统在低温时，很容易磁化，显示出超顺磁性特性。

b.系统分别在交换场、偶极场下的磁化行为

当系统只存在偶极场或交换场时候，系统的磁化曲线分别如图20中的（a）和（b）所示。当系统没有磁各向异性场时候，相当于先设单轴各向异性为常数。在模拟计算中取J＝1，且不记磁各向异性能项表示纯交换场的系统。同样的方式可以适用于D＝1，且不记磁各向异性能项表示纯偶极场的系统。由于此时单个纳米磁性颗粒不存在磁各向异性能，SW模型将不再适用，因此对这类系统采用是Metropolis算法。图（a）为纯偶极场作用下的系统，此类系统磁化曲线对温度不敏感，系统在低温时，出现一种特殊的快接近饱和区域的磁滞现象（圆圈部分所示），随着温度升高，这种磁滞现象消失，系统无磁滞特性；图（b）为纯交换场作用下的系统，此时系统将呈现矩形的磁滞回线。

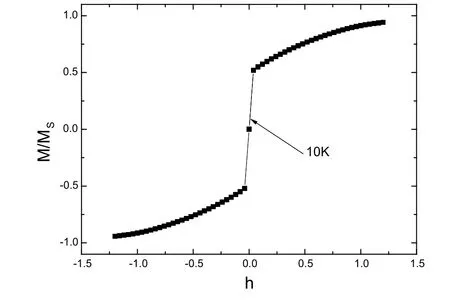
图19.采用Metropolis算法模拟出系统的磁化曲线，摘自文献[14]。

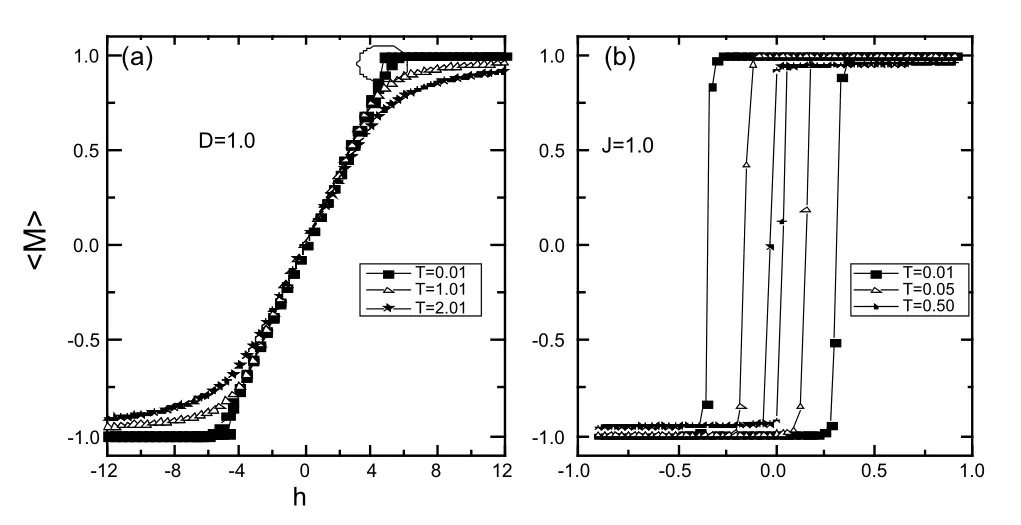
图20.颗粒之间只有交换作用或偶极作用时的磁化曲线，（a）图为只有偶极作用时的磁化曲线，此时D＝1，（b）图为只有交换作用时的磁化曲线，此时J＝1

c.各种能量项的综合作用

磁性小颗粒之间只有偶极作用的系统，系统在某个临界温度下将出现有序现象。简立方结构系统的基态是反铁磁性的，面心或者体心结构的系统的基态是铁磁性的，对无序的系统，基态可能出现自旋玻璃结构[39−41]。我们所研究的的系统是简立方结构的系统，系统的基态为反铁磁性的，因为交换作用是铁磁性的，因此系统受反铁磁性的偶极场与铁磁性交换场共同作用。研究这种竞争机制对实际材料有着比较重要的实际意义，这也是选择简立方结构的原因。图21中（a）、（b）、（c）、（d）分别为系统温度是0.01、0.05、0.1、0.5时，不同的偶极场常数下的磁化曲线，比较四个不同温度下的磁化曲线可以看出，随着温度的增加，系统的磁滞现象变弱直至消失。当系统的温度不变时，随着偶极场作用的增加，系统难磁化，对于有磁滞现象的系统，使发生磁滞现象的外磁场区域的变大，磁滞回线的形状变瘦。在图（c）中（T＝0.1），当系统没有偶极场作用时，系统没有磁滞现象（如图中标注D＝0.0曲线），随着D增加，系统出现瘦长形的磁滞回线。这种现象是由于纯偶极作用系统的临界温度较小（Tc＜0.1），偶极场与磁各向异性场共同作用的系统的临界温度比纯偶极场作用的系统的临界温度大所致。最后一定要注意的是，由于模拟中采用的合外场是外磁场与偶极场的矢量叠加，在SW模型中临界磁场hc为定值，当D增加，即偶极场增强，则相对应的外场的临界场减小，在高D作用下的系统，大多数颗粒都处于单能量极小态，此时我们所采用的修正的MC算法过度到Metropolis算法，这说明即使使用Metropolis算法，对有偶极场加磁各向异性场作用的系统也会模拟出磁滞现象42−44。

图21.不同温度不同偶极常数下系统的磁化曲线.摘自文献[37]。

图22中（a）、（b）、（c）、（d）分别为系统温度为0.01、0.05、0.1、0.5时，不同的交换积分常数下的磁化曲线。这四个不同温度下的磁化曲线一个统一的变化趋势是随着温度的升高系统的磁滞现象变弱直至消失，这和K＋D系统的变化趋势相同。从图（c）、（d）可以看出系统的温度升高，仅单轴各向异性系统没有磁滞现象，只有单轴各向异性和交换作用综合作用的系统才出现磁滞现象，由前面描述可知，仅J系统也能出现磁滞现象，因此得出结论J系统的磁滞温区大于K系统温区，所以导致K＋J系统的磁滞温区大于K系统温区。前面部分已得出结论K＋D系统的磁滞温区也大于K系统温区，但和这里不同的是，D系统没有磁滞现象。K＋J系统另一个比较显著的特点是：当系统出现磁滞现象时候，随J增加，系统的剩磁增加，而系统的矫顽力会出现先减小然后增加的特殊现象。系统剩磁可以从前面的叙述得到解释，矫顽力变化特点可以通过两种磁滞的竞争来说明：当J值较小时候，系统在低外磁场下，大多数颗粒都有两个稳定态，磁滞现象主要源于SW模型中小颗粒的不可逆畴转过程，在临界合外场一定的条件下，增加J值相当于减小了外磁场值，即导致矫顽力变小，随着J值进一步增加，系统即使在没有外磁场的作用时，交换场的值都大于临界场，此时由交换场引起的磁滞占统治地位，此时随着J增加，则系统的矫顽力自然增加。正是系统的两种磁滞机理的竞争导致系统出现特殊的矫顽力变化趋势。Wang等人就是利用K＋J系统来模拟无定形的磁性合金，选用局部动力学方法，我们认为这有不妥之处[45]。

图22.不同温度不同交换积分常数下系统的磁化曲线，摘自文献[37]。

C.磁化反转过程的实验观察

上述章节从理论上详细讨论了基于SW模型的磁性颗粒磁化反转的动力学过程。如今实验技术的发展已经可以测量单个磁性纳米颗粒的磁化过程，下面章节先介绍磁性纳米颗粒集合的常规探测方式，随后介绍两种典型的可以用于探测单个磁性纳米颗粒磁性的实验手段。

1.磁性纳米颗粒集合的集体磁化行为

SW模型为描述单畴磁性颗粒的磁化反转提供了很好的理论基础。各种物理以及化学方式已经可以制备出单畴磁性颗粒。但一般情况下，这些磁性纳米颗粒构成纳米颗粒集合，颗粒之间的相互作用、颗粒尺寸大小分布、单个颗粒的易磁化轴分布对整体的磁化行为都有影响。相关实验的结果都可以用SW模型加上各种相互作用来分析，其中典型的结果如下：

Wicht等人采用溅射的方式制备了（Fe55Pt45）0.7C0.3磁性颗粒薄膜，C的引入可以有效地减弱Fe55Pt45颗粒之间的相互作用[46]。他们的研究发现颗粒的磁化行为符合SW模型的理论结果，即当外磁场沿易磁化方向时，磁化曲线有很好的方型度，而当系统沿难磁化方向磁化时，磁化曲线呈现倾斜的形状，见图22。这种行为和图8种所示的单畴SW行为基本一致。

图23.（Fe55Pt45）0.7C0.3磁性颗粒薄膜磁性颗粒薄膜系统在外磁场分别沿难磁化与易磁化方向时候所测量得到的磁化曲线。内插图为（Fe55Pt45）0.7C0.3磁性颗粒薄膜的形貌图，摘自文献[46]。

Baranov等人采用分子束外延的方式在有台阶的CaF2（110）/Si（001）衬底上沉积MnF2磁性颗粒[47]。由于衬底的影响，MnF2磁性颗粒呈线性排列，颗粒之间的偶极相互作用导致强的磁各向异性。当外磁场沿线方向时候，磁滞回线呈现很好的方型度，而当外磁场垂直线方向时候，磁滞回线呈现蜂腰状。这个实验结果偶极相互作用起主导地位的SW模型，见图21。

另外,化学方式可以制备出核/壳纳米颗粒。通过在磁性纳米颗粒外面包裹非磁性材料，可以有效地避免纳米颗粒之间的交换作用，并且还可以调节纳米颗粒之间偶极相互作用。例如Yang等人利用化学方式合成了纳米颗粒之间距离可控的Fe2O3-SiO2核/壳磁性纳米颗粒集合[48]。通过测量交流磁化率,他们发现系统的动力学行为符合由SW模型给出的单畴磁纳米颗粒的驰豫规律,进而确认纳米颗粒之间无交换作用。相关的基于SW模型的MC计算也表明在无铁磁交换作用的单畴磁纳米颗粒系统，当偶极相互作用能和磁各向异性能的大小比例小于10−4时,偶极相互作用能的影响可以忽略，见图23。通过计算Fe2O3-SiO2核/壳磁性纳米颗粒的各个能量项,发现这个理论计算的结果可以很好的解释实验观察到的现象49。

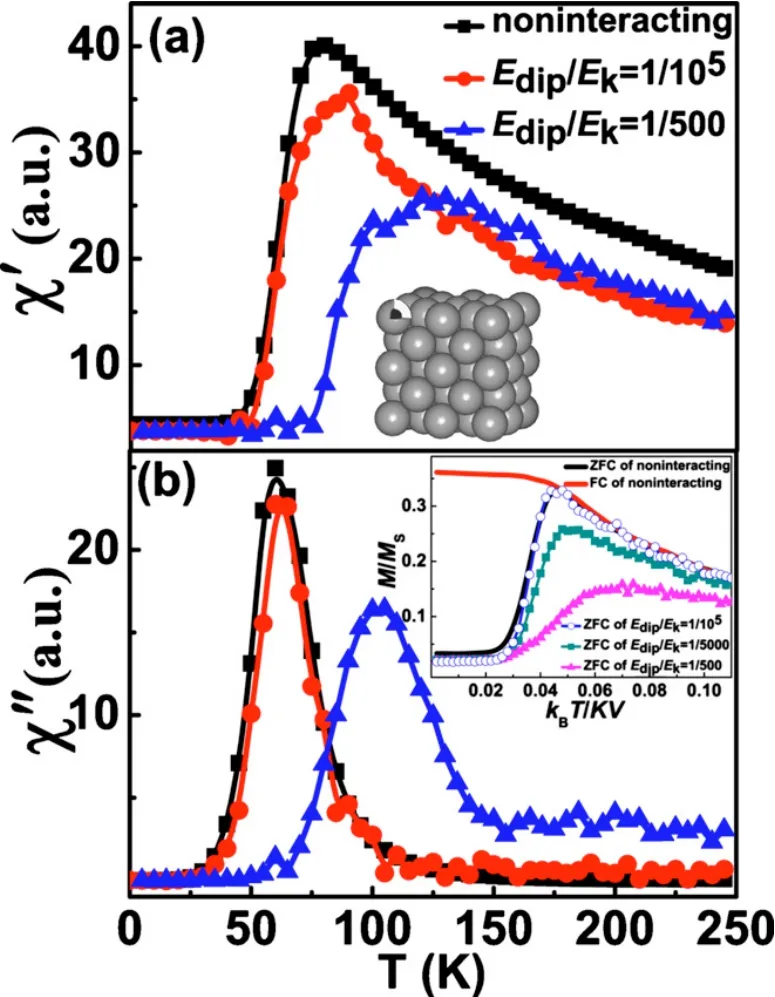
图24. MC模拟得到的磁性纳米颗粒集合在不同的距离时，交流磁化率随温度的变化关系，摘自文献[49]。

2.单个颗粒磁化反转过程的磁共振力显微镜探测[50−54]

目前常用的SQUID VMS磁强计可以直接测量样品的磁矩，但是精度不足以探测单个纳米磁性。目前实验技术的发展已经使得测量单个磁性纳米颗粒的磁学特性成为可能。在本节以及下面的章节中，我们将介绍两个有代表性的方式，即：磁共振力磁强计以及电子全息技术。

瑞士巴塞尔大学Poggio组采用基于灵敏悬臂梁的力矩磁化分析比商业SQUIDVMS磁强计更高的磁性检测精度（可达10−15emu），可以测量纳米材料单体的磁性，观测其磁化过程。力矩磁化分析的原理是：当磁性样品处于外加磁场下，当其易磁化轴偏离外磁场方向时，磁性样品会受到一个力矩使其转回外磁场方向，这个力矩可以通过灵敏的悬臂梁测量，基本工作原理如图22所示。

图25.利用灵敏悬臂梁进行力矩磁化分析。当磁性样品处于外加磁场下，当其易磁化轴偏离外磁场方向时，磁性样品受到的力矩正比于外加磁场和材料的磁矩，摘自文献[50]。

Poggio组利用上述设备成功的测量出单根纳米管的磁化反转过程。图23为多晶镍纳米线的悬臂梁在不同外加磁场方向下的共振频率随磁场强度的变化。通过基于SW模型的理论分析，可以得出这些频率变化正比于外加磁场的强度和镍纳米线的磁化强度。

此项技术主要用于磁性纳米线的研究。原则上，本项技术也可以很方便的扩展到纳米颗粒系统，特别是单畴颗粒，可以严格的测量单个纳米颗粒的磁化过程。我们期待相关的实验结果。

3.单个颗粒磁化反转过程的电子全息技术探测[55−56]

最近几年来，随着场发射电子显微镜的不断发展，为电子全息术提供了高亮度的单色电子束源，使电子全息技术日臻成熟。用电子全息术观察微电磁场结构成了物理学领域中的一个活跃分支。1967 年Cohen首次用电子全息术给出了磁畴结构的直观信息，随后Tonomura，Pozzi和Missiroli用电子干涉术验证了磁畴结构确实影响电子的位相。Wahl 和Lau对此还进行了理论研究。1980年Tonomura首次采用电子全息法观察到铁氧体微粒内的磁畴结构。自此人们把电子全息术作为一个有效的工具用来研究磁性材料和微磁场结构。由于电子全息图中包含了电子波的全部信息，所以采用电子全息法不但可以定量地测出微磁畴精细结构，见图24。而且当采用光学方法重现时，在非成象位置还可以获得Lorentz显微象。这种方法的优点是分辨率高，可以研究磁畴的精细结构，同时也可以在不同温度和外场下进行观测。但需要操作人员掌握一定的全息光学知识与技能。

图26.单根多晶Ni纳米线的磁化过程以及相对应的磁化态，摘自文献[54]。

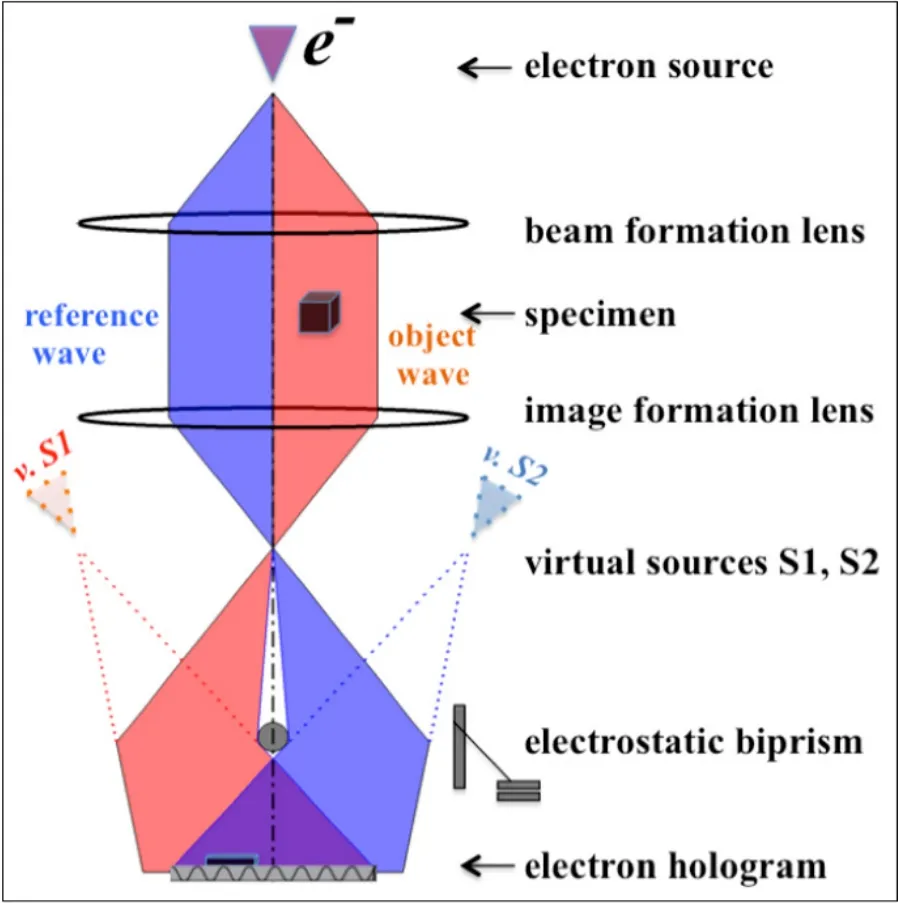
图27.电子全息技术基本原理，摘自文献[55]。

德国尤利西研究中心Rafel研究组利用高分辨的德电子显微全息技术，成功地观测到了单个磁性纳米颗粒以及纳米颗粒集合的磁感应线分布，见图25，从中可以明显地推断出纳米颗粒的单畴结构以及由于纳米颗之间偶极相互作用导致的磁结构。

图28.两个磁纳米颗粒的基态磁感应线分布。（a），两个纳米颗粒的形貌图；（b），电感应强度分布；（c），磁感应强度；（d），磁感应强度的磁力线分布，摘自文献[55]。

III.总结与展望

本文详细论述了纳米颗粒的磁化反转过程所依赖的基本物理的SW物理模型以及基于此模型的计算机模拟方法。SW模型在描述单畴磁性纳米颗粒的磁化反转行为取得了很得成功。我们注意到最近的理论发展进一步扩展SW模型到多个磁各向异性的情况以及近单畴磁性颗粒系统[58,59]。但是对单个单畴磁性纳米颗粒的磁化反转行为的具体检验还有待开展。我们所探讨的磁共振力磁强计以及电子全息技术提供了很好的实验方法，我们期待进一步相关的工作。值得说明的是：磁性纳米颗粒是一种多功能磁性纳米粒子材料，在磁记录材料、磁流体、催化、医药、颜料等领域具有广泛的应用[60,61]。本文对理解相关应用领域的行为提供了一个很好地理论基础。

致谢

本项工作得到了中国科学院青年促进会专项基金的资助（No. 2015267）

参考文献

[1]张志琨,崔作林.纳米技术与纳米材料,北京：国防工业出版社, 2002

[2]张立德,牟季美.纳米材料与纳米结构,北京：科学出版社, 2001

[3]都有为.纳米磁性材料及其应用,中国高校科技与产业化, 2002, 7：36-39

[4]宛德福,马兴隆.磁性物理学,北京：电子工业出版社, 1999

[5] MΦrup S, Chrisiansen G, J. Appl. Phys., 1993, 73（10）：6955

[6] Goll D, Berkowitz A E, Bertram H N, Phys. Rev. B, 2004, 70（18）：184432

[7] Kittel C, Galt J K, Campbell W E, Phys. Rev. B, 1995, 77：725.

[8]钟文定.铁磁学（中）,北京：科学出版社, 1998

[9]李伯臧. Brown方程的分歧解与初始成畴问题,物理学报, 1981, 12.

[10]成立,范建中. Stoner-Wohlfarth模型中的几个表达式,江苏理工大学学报, 1996, 17（2）.

[11] Jamet M, Wernsdorfer W, Thirion C, Dupuis V, M´elinon P, P´erez A, Mailly D, Phys. Rev. B, 2004, 69（2）：024401.

[12]王兴元,朱伟勇,顾树生,一般二维二次映射中的混沌与分形,计算机辅助设计与图形学学报, 2000, 12, 408.

[13]周伯熏.高等代数基础,北京：高等教育出版社, 1989：40-42

[14] Du H F, and Du A, J. Appl. Phys., 2006, 99（10）：104306

[15]冯端,师昌绪,刘治国.材料科学导论,北京：化学工业出版社, 2004：669-696

[16]高英俊,刘慧,钟夏平, Journal of Guangxi University, 2001, 26（4）, 114

[17]夏宗宁,贺立,吕允文.材料科学中的计算机拟,化工新型材料, 1996, 24（2）：124

[18] D. Robert编著,项金钟,吴兴惠译.计算材料学,北京：化学工业出版社, 2002：51-112

[19] Heermann D W著,秦克诚译,理论物理学中的计算机模拟方法,北京：北京大学出版社, 1996：145-174

[20] Landau D P, Binder K. A Guide to Monte Carlo Simulations in Statistical Physics,北京：世界图书出版社, 2000

[21] Knuth D. The Art of Computer Programming, Boston：Addison-Wesley Reading, MA, 1969, Vol.2.

[22] Ahrens J H, Dieter U. Pseudo Random Numbers, New York：Wesley, 1979.

[23]何光渝,高永利. Visual Fortran常用数值算法集,北京：科学出版社, 2002.

[24]中国科学技术大学高等数学教研室,高等数学导论（中册）,合肥：中国科学技术大学出版社, 1996：265-267.

[25] Hansen M F, MΦrup S. J. Magn. Magn. Mater., 1998, 184：262-274.

[26] Dormann J L, Bessais L, Fiorani D, J. Phys. C：Solid State Phys., 1998, 21：2015-2034.

[27] Sorge K D. Magnetic Properties of Nanoparticles Systems of Fe, Co, Ni and FePt, Created by Ion Implantation[D], 2002：27-34.

[28] Andersson J-O, Djurberg C, Jonsson T, Svedlindh P, Nordblad P, Phys. Rev. B, 1997, 56（21）：13983.

[29] Wang L, Ding J, Kong H Z, Li Y, Feng Y P, Phys. Rev. B, 2001, 64（21）：214410.

[30] Dimitrov D A, Wysin G M, Phys. Rev. B, 1996, 54（13）：9237.

[31] Garc´ıa-Otero, Porto J, Rivas M, Bunde J, J. Magn. Magn. Mater., 1999, 203：268-270.

[32] Jalil M B A, J. Appl. Phys., 2003, 93（10）：8050.

[33] Papusoi C, Jr, Stancu Al, Dormann J L, J. Magn. Magn. Mater., 1997, 174：236-246.

[34] Xu C, Li Z Y, Hui P M, J. Appl. Phys., 2001, 89（6）：3403.

[35] Chantrell R W, Weller D, Klemmer T J, Sun S, Fullerton E E, J. Appl. . Phys., 2002, 91（10）：6866.

[36] Andersson J -O, Djurberg C, Jonsson T, Svedlindh P, Nordblad P, Phys. Rev. B, 1996, 56（21）：13983.

[37] Du H F, and Du A, Phys. Stat. Sol.（b）, 2007, 244（4）：1401-1408

[38] Jamet M, Wernsdorfer W, Thirion C, Dupuis V, M´elinon P, P´erez A, Mailly D, Phys. Rev. B, 2004, 69（2）：024401.

[39] Luo W L, Sidney R, Nagel T F, Rosenbaum, Rosensweig R E, Phys. Rev. Lett., 1991, 67（19）：2721—2724.

[40] Mørup S, Bødker F, Hendriksen P V, Linderoth S, Phys. Rev. B, 1995, 52（1）：287.

[41] Mørup S, Christensen P H, Clausen B S. J. Magn. Magn. Mater., 1987, 68：160.

[42] Kechrakos D, Trohidou K N, Appl. Surf. Sci., 2004, 226：261-264.

[43] Kechrakos D, Trohidou K N, J. Magn. Magn. Mater., 2003, 262：107-110.

[44] Kechrakos D, Trohidou K N, Appl. Phys. Lett., 2002, 81（24）：4574.

[45] Wang L, Ding J, Kong H Z, Li Y, Feng Y P. Phuc N X, Dan N H, J. Appl. Phys., 2001, 89（12）：8046.

[46] Wicht S, Neu V, Schultz L, Weller D, Mosendz D, Parker G, Pisana S, Rellinghaus B, J. Appl. Phys., 2013, 114：063906.

[47] Baranov D A, Krichevtsov B B, Gastev S V, Banschikov A G, Fedorov V V, Koshmak K V, Suturin S M, Sokolv N S, Appl. Surf. Sci. 2013, 267, 196-699,

[48] Yang H T, Hasegawa D, Takahashi M, Ogawa T, Appl. Phys. Lett. 2009, 94：013103.

[49] Yang H T, Liu H L, Song N N, Du H F, Zhang X Q, Cheng Z H, Sheng J, Li L F, Appl. Phys. Lett. 2011, 98：153312.

[50] Webert D P, R¨uffer D, Buchter A, Xue F, Russo-Averchi E, Huber R. Berberich P. Arbiol J, Fontcuberta i Morral A, Grundler D, and Poggio M, Nano Lett., 2012, 12：6139-6144

[51] Jang J, Ferguson D G, Vakaryuk V, Budakian R, Chung S B, Goldbart P M, Maeno Y, Science, 2011, 331：186-188

[52] Banerjee P, Wolny F, Pelekhov D V, Herman M R, Fong K C, Weissker U, M¨uhl T, Obukhov Y, Leonhardt A, B¨uchner B, Hammel P C, Appl. Phys. Lett., 2010, 96（25）：252505

[53] Nagel J, Buchter A, Xue F, Kieler O F, Weimann T, Kohlmann J, Zorin A B, R¨uffer D, Russo-Averchi E, Huber R, Berberich P, Fontcuberta i Morral A, Grundler D, Kleiner R, Koelle D, Poggio M, Kemmler M, Phys. Rev. B, 2013, 88：064425.

[54] Buchter A, Nagel J, R¨uffer D, Xue F, Weber D P, Kieler O F, Weimann T, Kohlmann J, Zorin A B,Russo-Averchi E, Huber R, Berberich P, Fontcuberta i Morral A, Kemmler M, Kleiner R, Koelle D, Grundler D, Poggio M, Phys. Rev. Lett., 2013, 111（6）：067202.

[55] Midgley, P. A., Dunin-Borkowski, R. E, Nature Mater., 2009, 8：271-280.

[56]田焕芳李建奇电子全息及其在材料科中的一些应用,科学通报, 2006, 51：1617.

[57] Kuncser A, Kuncser V, J. Magn. Magn. Mater., 2015, 395：34-40.

[58] Campos M, Silva F, Perigo E, Castro J, J. Magn. Magn. Mater., 2013, 345：147-152.

[59] Cimpoesu D, Stoleriu L, Stancu A, J. Appl. Phys., 2013, 114：223901.

[60] Zhang Y D, Zhang Y, Pan Y F, China Medical Engineering, 2006, 14：148-152.

[61]徐星星,朱宏,磁性材料及器件2009年10月综述.

Invesitigation on the Magnetization Reversal of Magnetic Nanoparticles Based on Stoner-Wohlfarth Model

Wei Wen-Sen1,2, Du An3, Du Hai-Feng1∗

1. High magnetic Field Laboratory, Chinese Academy of Sciences, Hefei 230031, China
2. Hefei National Laboratory for Physical Sciences at the Microscale, University of Science and Technology of China, Hefei 230026, China
3. College of Sciences, Northeastern University, Shenyang 110004, China

Magnetic nanoparticles have been applied in many fields due to their novel properties. From the viewpoints of fundamental research, lots of theories have been proposed. On the other hand, with the development of experimental measurements and numerical simulations, it is possible to investigate the magnetic properties of single magnetic nanoparticle and then design the desired assemble. In this review, we introduce the magnetization reversal of magnetic nanoparticles, focusing on the related theories and latest experimental techniques. We first introduce the basic magnetic interaction at the nano-scale, which is followed by introducing the numerical simulation of magnetization reversal of magnetic nanoparticles based on Stoner-Wohlfarth model. Finally, twotypical techniques, detecting the magnetization reversal of magnetic nanoparticles, are overviewed.

Key words:magnetic nanoparticles; magnetization reversal; stoner-wohlfarth model; monte carlo simulation; magnetic resonance microscopy; electron holography

文章编号：1000-0542（2016）01-0001-201

中图分类号：O482

文献标识码：A

DOI:10.13725/j.cnki.pip.2016.01.001

Received date：2015-12-24