基于SVM的精密指针式仪表自动读数方法

石 睿 谢将剑 赵 暄 李剑禹

（北京林业大学 工学院，北京 100083）

基于SVM的精密指针式仪表自动读数方法

石 睿 谢将剑 赵 暄 李剑禹

（北京林业大学 工学院，北京 100083）

针对精密指针式仪表读数算法对自动读数的自适应性差问题，提出一种基于SVM的精密指针式仪表自动读数方法。该方法首先对二值化处理后的仪表图像通过面积形态学提取刻度并做极坐标变化，再利用面积形态学特征提取刻度与指针位置，最后利用SVM识别刻度对应的数值进行读数判读。实验表明，自动读数结果与实际数值相比误差均小于0.1%，算法稳定可靠。

指针式仪表 支持向量机 数字识别 标准差分析

引言

精密指针仪表抗电磁干扰能力强、精度高、价格低，广泛应用于检定计量、电信号测量等领域。但是，指针式仪表输出结果为非数字信号，难以通过系统直接读数，所以近年实际应用中通常采用自动方法[1]来提高读数效率。目前，读数方法一般分为指针提取与刻度定位两种。指针提取方法主要使用影差法或者Hough变化等直线提取方法，如李治玮等通过模板图像与实际图像做影差提取指针位置[2]；张冀等采用影差法提取指针，并通过Hough变换获得指针角度加以处理[3]；施健等采用背景差分法分割指针，利用Hough拟合计算指针夹角[4]；房桦等首先对仪表表盘区域二值化、细化处理，然后通过Hough变换提取指针[5]；Han等提出一种基于改进Hough变换的算法提取指针直线角度读取读数[6]。刻度定位方法较多，常用的是使用神经网络模型方法或者形态学处理的方法，如王三武等采用Hough变换提取指针信息，并选用神经网络模型的方法优化指针提取结果[7]。

上述读数方法虽已取得了一定成果，但均需将指针不同旋转角对应的值提前写入读数算法。由于实际应用中仪表与相机位置常常不能保证相对稳定，因此读数时每次都需要预先设定指针不同位置对应的读数，即算法的自适应性低。针对这一问题，本文在对精密指针式仪表的特性后引入面积形态学提取的方法进行刻度的提取，提出一种基于SVM的精密指针式仪表自动读数方法，从而对指针仪表上的刻度值进行字符识别。

1 指针仪表图像预处理部分

1.1 指针仪表刻度提取

图1为采集的指针仪表图像。读数前，为剔除光照不均影响以及一些不必要信息，有必要对其进行二值化处理。考虑精密指针仪表图像刻度分布连续且面积较大，并需要同时消除读数反射镜对二值化的影响，本文选择Sauvola二值化方法[8]。

本文的二值化方法定义为：

图1 图像采集结果

其中，迭代的窗口大小选择为15×15的矩形窗，m(x,y)为窗口中像素灰度的标准差，k为标准差因子，s(x,y)为窗口内的标准方差，R=128，T(x,y)为动态阈值。计算每个窗口内像素点的s(x,y)和m(x,y)，以此作为判断图像噪声的标准。该算法可以将完全连通在一起的区域（如读数反射镜区域）进行分离。在二值化区分算法中，设定标准差因子对去噪灵敏度进行调节，可以在光照分布不均时有效保留刻度区域。算法运行效果，如图2所示。

图2 局部均值标准差分析二值化结果

由运行结果可以看出，本文所采用的二值化方法可以有效将刻度与指针等区域分割，消除了光照和读数反射镜对表盘的影响。

1.2 极坐标变化

精密指针仪表刻度密集且为非均匀刻度，所以在弧形刻度中实现读数往往会由于角度原因影响读数精度。本文选择通过刻度圆弧进行圆弧拟合，并通过极坐标变化将图像转换到对数极坐标系，将弧形刻度转换为直线刻度进行处理。极坐标变换如式（2）、（3）所示：

2.2 .1 SVM支持向量机

SVM是一种实用的数据分类器，一般认为比神经网络更容易应用。SVM的目标是生成一个可以预测目标值的模型[9-11]，给定一组点(xi,yi)，i=1,...,l，这里xi∈Rn,y∈{1,-1}l，则SVM实际要求解下面这个最优化问题：

训练向量xi投影到一个被φ定义的高维空间，SVM就是在这个高维空间中找到一个线性可分的超平面。C>0是训练误差的惩罚参数。K(x,x)≡φ(x)Tφ(x)是核函数，本文

ijij选择径向基核函数（RBF），其中K(xi,xj)=exp(-γ||xixj||2)，γ=0.02为核参数。

2.2 .2 训练样本的设定

由于本文的识别针对仪表刻度上的数字，因此本实验所用的样本是经过对仪表照片进行一系列处理而提取出来的。为了方便后续的识别工作，这些样本统一转化为8×8的标准尺寸，刻度值样本如图6所示。

其中：ρ、θ分别对应对数坐标系的极径和极角，x0、y0为变换中心，x、y为变换前坐标系像素点。变化后，图像如图3所示。

图3 极坐标变换图像

2 基于SVM的自动读数

2.1 指针与刻度位置提取

提取指针位置与刻度位置并计算它们的相对距离，是完成自动识别读数的最后步骤。从图3可见，极坐标变换后的图像中，下方空白区域指针明显。因此，本文设定刻度下方只有指针存在的白色区域为感兴趣区域，此时采用本文提出的二值化算法即可分割出指针。同理，设定刻度上方只有数字区域为感兴趣区域，通过本文提出的二值化算法区分出数字位置，选择欧氏距离相近的数字将其分别生成数字块，如图4所示。由图4可见，数字10、20、30等均可以定位到其对应的刻度上方，以每个数字块的中心点坐标为大刻度坐标值，则提取出刻度与指针的需要信息，如图5所示。

图6 刻度数字样本

图4 刻度值位置

图5 指针位置提取结果

2.2 SVM数字区域识别

在提取到指针与刻度位置后，在刻度上方分割出数字区域，并对数字区域做字符识别。根据数字对应的刻度坐标，可以实现指针与刻度的自动读数，避免图像中指针仪表位置变动时刻度坐标值发生变化导致读数失败的问题。考虑到刻度值均为工业印刷体数字，属于小样本分类字符识别问题，本文选择SVM分类器进行字符识别。

根据数字识别的特性，选择输入样本的八通道梯度值和样本横纵比作为训练样本的分类特征定。计算八通道梯度值时，首先将梯度方向离散到八个方向，然后幅值图像根据离散的八个方向被分解到八个通道，而每个通道以5×5大小的窗口进行梯度计算。

2.2 .3 Nu-SVM训练与识别

一般将多个两类SVM分类器结合在一起实现多分类，而本文采用其中的1-a-1（1-against-1）方法进行分类。多类分类方法的分类原理是在每两类间训练一个两值SVM分类器，从而得到k(k-1)/2个分类器（假设总类别数是k,k≥2）。

刻度数字种类共9个，分类算法针对二分类问题提出，而刻度数字识别需要解决的是多分类问题多类分类器的方法。本文采用间接法，主要通过组合多个二分类器来实现多分类器的构造。具体的，采用一对一法，即在每两个数字之间设计一个分类器。在选取核函数参数时，本文采用交叉验证的方法找到最优参数。

为了控制训练误差，本文选择改进的Nu-SVM创建支持向量机：

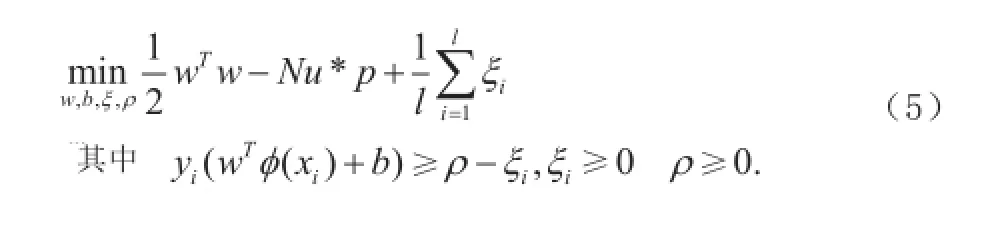
作为一个渐进上边界，Nu∈[0,1]可以控制训练误差，取值为0.05。训练样本后，对分割出的数字区域进行识别，效果如图7所示。

图7 刻度数字识别效果

2.2 .4 读数判读

如图5、7所示，刻度与指针相对位置均已提取，可以判定指针与刻度的相对位置。结合对刻度值数字的自动识别结果，可以自动生成每个刻度坐标对应的实际值，从而通过对指针与大刻度相对位置的计算，实现距离法判读。

3 实验结果分析

为了验证本文算法的有效性，利用Manta-504B型号工业相机搭建精密指针式仪表图像采集系统，测定对象为0.2级精度电压表T24-AV。测试数据如表1所示。

表1 实验运行数据

由表1可见，算法可以准确获取读数值，且读数精度与运行时间满足实际需要。需要注意的是，表中时间不包括训练样本所需时间，只包含SVM分类的时间。

4 结论

本文提出了一种基于SVM的精密指针式仪表自动读数方法，包括仪表图像预处理、SVM识别刻度并读数两个部分。预处理部分：根据精密指针仪表刻度连续分布的特征，改进基于标准差分析二值化预处理方法；分割出刻度与指针后，通过刻度区域进行极坐标变化，为后续提取刻度与指针相对位置提供条件。识别与读数部分：对极坐标图像进行二值化与面积形态学分割，得到刻度与指针相对位置，提出采用SVM识别刻度上方数字部分的方法，解决传统读数算法中自动化程度低的问题。实验结果与实际值相比，相对误差均小于0.1%。可见，该算法稳定可靠，增强了系统自适应性，运行时间满足实用需求。

[1]MOGHADDAM R F，CHERIET M.A Multi-scale Framework for Adaptive Binarization of Degraded Document Images[J]. Pattern Recognition，2010，43（6）：2186-2198.

[2]李治玮，郭戈.一种新型指针仪表识别方法研究[J].微计算机信息，2007，（31）：113-114，126.

[3]张冀，王俊宏，尉迟明，等.基于计算机视觉的汽车仪表指针检测方法[J].计算机工程与科学，2013，35（3）：134-139.

[4]施健，张冬，何建国，等.一种指针式化工仪表的远程抄表设计方法[J].自动化仪表，2014，35（5）：77-79.

[5]房桦，明志强，周云峰，等.一种适用于变电站巡检机器人的仪表识别算法[J].自动化与仪表，2013，28（5）：10-14.

[6]温和，滕召胜，杨圣洁，等.基于计算机视觉的指针式仪表智能判读方法[J].仪器仪表学报，2007，28（7）：1234-1239.

[7]王三武，戴亚文.多指针水表自动识别系统[J].仪器仪表学报，2005，26（11）：1178-1181.

[8]Bovik A L.Handbook of Image and Video Processing[M].New York：Academic Press，2000.

[9]Astorino A，Gorgone E，Gaudioso M，et al.Data Preprocessing in Semi-supervised SVM Classification[J]. Optimization，2011，60（1-2）：143-151.

[10]蒋华，戚玉顺.基于球结构SVM的多标签分类[J].计算机工程，2013，39（1）：294-297.

[11]奉国和.SVM分类核函数及参数选择比较[J].计算机工程与应用，2011，47（3）：123-124.

Auto-reading Method for Precision Pointer Meter Based on Intersect Cortical Model

SHI Rui, XIE Jiangjian, ZHAO Xuan, LI Jianyu
(School of engineering, Beijing Forestry University, Beijing 100083)

Aiming at the problem of adaptivity in autoreading method for precision pointer meter, an auto-reading method for precision pointer meter based on support vector machine (SVM) is proposed. Firstly, the proposed approach extract the scale by area of morphological features of binary meter image, and polar transformation image is derived by information of arc of the scale. Secondly, the scale and index are extracted in polar transformation image using max-area information of binary polar transformation meter image. Finally, the digits of the scale values are recognized by SVM, and the meter reading is calculated by the relative position between scale and index. Experimental results show that the relative error between meter auto-readings and actual readings is less than 0.1% and the method is reliable.

pointer meter, support vector machine, digits recognition, standard deviation analysis

中央高校基本科研业务费专项资金资助（2016ZCQ08）。