动态拖尾星图模拟算法研究
2016-04-07武延鹏
鹿 瑞,武延鹏
(北京控制工程研究所,北京100190)
动态拖尾星图模拟算法研究
鹿 瑞,武延鹏
(北京控制工程研究所,北京100190)
星图模拟技术是星图识别算法仿真和性能测试的基础.为了更好地模拟星敏感器在轨工作的情况,对星敏感器的软件开发以及自身性能进行有效的地面测试,提出一种动态拖尾星图模拟算法.该算法分为4个步骤:首先根据星敏感器指向在全天球范围内搜索导航星;接着利用小孔成像模型计算导航星在星敏感器成像面的投影位置;然后在考虑卫星运动引起的恒星拖尾的基础上,按照二维灰度分布规律置灰度值来模拟星像点像素;最后叠加杂散光背景及成像器件引起的噪声.提出的算法具有速度快、精度高及可实现性高等优点.
星敏感器;星图模拟;卫星轨道运动;像移
0 引言
星敏感器是以恒星作为测量目标的光学姿态测量敏感器,能够输出高精度的姿态信息,是实现卫星控制分系统上水平的关键光学姿态测量部件[1].
伴随着空间技术的发展,对星敏感器的性能指标也提出了越来越高的要求.相应地对星敏感器的标校和检测也提出了越来越高的要求.由于航天试验费用巨大,往往不可能实时开展空间试验,所以必须建立地面模拟仿真平台在地面模拟星空.通常地面测试方法有两种:一种是外场观星测试[2],即在一个空旷、大气环境相对较好以及杂散光相对较弱的真实地面环境下,将星敏感器放在转台上,进行实地观星测试.这种方法简单易行,但是受天气影响较大,而且对转台设备精度要求很高,不能保证随时测试的要求,而且费时费力,无法模拟星敏感器的在轨状态.另一种方法就是采用星模拟器进行星敏感器地面测试[3],这种方法又分为静态和动态两种,静态星模拟器由点光源和一系列滤光片组成,主要用于模拟单个星点成像,对其大小、光度(星等值)张角、星等光谱特性进行模拟以便对星敏感器的探测能力、空间分辨率等进行地面定标.静态星模只有固定的星点构型,而且通常设计指标固定,只能为一种固定类型的星敏感器产品服务.动态星模拟器[4]通常和被测星敏感器、主计算机组成闭环测试系统,将星图模拟程序产生的星图,实时地送到高分辨率液晶显示屏上,照明系统照亮液晶光阀产生模拟星点,再由光管送到星敏感器,实现星敏感器观测星空的实时模拟.而目前的星模拟器一般是针对卫星平稳运行情况下的模拟,无法给出卫星在高机动情况下的模拟[5].无论是静态星模还是动态星模都没有考虑卫星轨道运动及像移对星图模拟的影响.文献[6]仅考虑了个平稳随机振动过程,未考虑背景噪声,与实际情况有很大差距.文献[7]虽然考虑了卫星轨道运动及像移对星图模拟的影响,但是背景单一,未考虑任何背景噪声影响.
为了克服以上问题,本文提出了一种考虑卫星轨道运动和像移影响的全天球动态星图模拟算法.该算法可以实现在全天球范围内模拟动态拖尾星图,采用分区检索的方法,对按赤经、赤纬对全天球进行划分,从而提高了导航星检索的速度,满足星模拟器的实时性要求.该算法采用了基于高斯分布的星点灰度扩散方法,严格准确地模拟了实际星像点灰度散焦的高斯特性.该算法考虑太空的背景噪声、成像器件及电路的噪声,较为准确地模拟了背景星图.该算法还考虑了卫星轨道运动引起的恒星像移,能够比较真实的模拟星敏感器在轨运动过程中采集的星图.除此之外,本方法不仅可以产生单幅星图,而且可以产生任意时间段的连续的星图序列.
1 星图模拟原理
星模拟器主要为星敏感器提供地面模拟仿真测试平台.首先,随机确定视轴方向,包括视轴指向的赤经、赤纬以及旋转角度.其次,根据坐标变换,将基本星表里的导航星从天球坐标变换到像平面坐标,得到导航星点在像平面的精确坐标.接着,根据星等变换关系,将导航星星等变换成对应的图像灰度值.最后叠加背景噪声.星图模拟流程图如图1所示.

图1 星图模拟流程图Fig.1 Star image simulation flow
2 星图模拟算法介绍
2.1 导航星检索
首先产生一个随机指向,根据星图的积分时间和卫星的角速度,计算每帧星图拍摄时的光轴指向.然后根据光轴指向在全天球范围内检索导航星.若采用简单的直接搜索的方法,光轴每变化一次,就需要把星表内所有星检索一遍,才能查找到视场内的星.为了快速检索到导航星,根据星敏感器的视场,建立导航星表的快速索引.例如某星敏感器视场为8.9°×8.9°,其导航星表共有29 666颗导航星,建立了481个索引块,任意一个指向,大约搜索5个索引块即可找到该指向对应的导航星,如此搜索时间大约为全天区搜索方式的1%.
2.2 星点能量计算
星等是星体亮度的表征.星体的亮度[4]是以在地球大气层外接收到的恒星辐射照度来衡量的,其关系如式(1)所示:
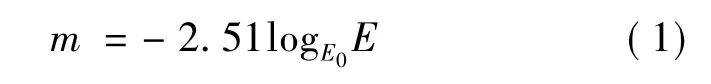
式中:E表示辐射照度;E0为零等星的辐射照度;m为星等.式(1)表明辐射照度越大,星等越小.仪器星等决定于接收仪器所用的探测器的光谱特性.仪器星等可由式(2)计算

式中,ES表示探测器敏感到的辐射照度;ES0为探测器敏感到的零等星的辐射照度;mi为仪器星等.若已知星点的仪器星等,探测器敏感到的辐射照度,即星点的总能量可按式(3)计算

为此,首先需要星敏感器的参数设置,如星敏感器的分辨率,视场,光学系统透过率,量子效率等,计算探测器敏感到的零等星的辐射照度,然后根据恒星的仪器星等,计算探测器敏感到的辐射照度,即星点的能量.
2.3 基于高斯分布的星像点精确模拟
为提高星敏感器仿真系统的精度,提出了基于高斯规律的模拟星像点的灰度扩散算法.首先将导航星在惯性坐标系中的坐标转换到像面坐标系,此为星像点的质心坐标,然后以此质心坐标为中心,开展基于高斯分布的灰度扩散.
为了获得更高的恒星定位精度,星敏感器一般采用离焦技术,使得实际探测面上的恒星像点是一个分布在几个像元上的模糊斑点.在静态条件下,星点在像面上的能量分布可用二维高斯(Gauss)函数表示

式中:I表示在单位时间内所接收到的信号能量总和,由星等、镜头口径、探测器量子效率等因素决定; (x0,y0)表示星点能量分布的中心,即恒星在星敏感器成像面上的投影位置;表示星点能量分布的高斯半径,主要取决于光学设计阶段的像差优化和像面离焦位置.
在对恒星成像过程中,由于星敏感器和恒星的相对角运动,会产生像移.通常,星敏感器的曝光时间较短(<0.25 s),可近似认为星点在像面上匀速运动[6].设星点在探测器像面上像移速度为(u,v),当曝光时间为t0时,第(i,j)像元接收到的星点能量信号为
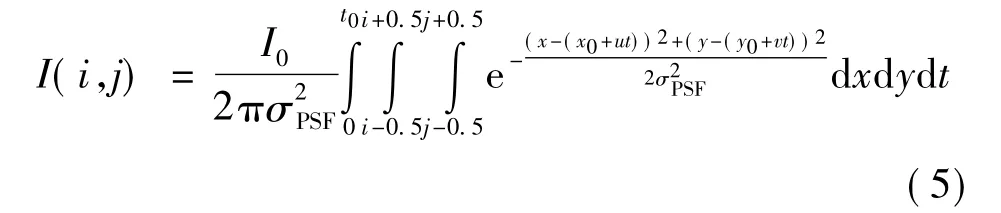
式(5)中,(i,j)的取值为以(x0,y0)为中心的邻域,具体大小取决于恒星像斑大小.
为了提高仿真的精度,将星像点在15×15的窗口内开展扩散,并且对每个星像点开展128×128的亚像元高斯拟合,高斯分布模型如图2所示.基于该模型计算质心位置误差仅为0.017 6个像素.
2.4 噪声分析与建模
星敏感器噪声有两大来源:一是星空背景噪声,主要是指来自太阳和地球的杂散光;二是成像器件本身的噪声,主要有成像器件引起的暗电流噪声、暗电流不均匀性噪声、光响应不均匀性噪声、读出噪声等[8-10].
2.4.1 星空背景噪声
有两种方式叠加星空背景噪声,一种是在杂散光实验室拍摄星图,将其作为星点叠加的基础;另外一种方式为利用拍摄的杂散光星图,统计出星图的背景和方差,然后根据正态分布拟合星空背景噪声.
2.4.2 成像器件的噪声
与星空背景噪声一样,成像器件的噪声亦有两种不同的方式获取:一种为盖住镜头盖,拍摄一幅黑图,该方式拍摄图即可以作为成像器件引起的噪声开展后续工作;另外一种方式为根据器件手册指标或实验室测试值建模分析.
(1)光子散粒噪声
入射星光信号的光子进行随机的不规则运动形成光子散粒噪声.它是图像传感器固有的噪声,不能被后续电路抑制或抵消.
(2)暗电流噪声
光电子由于热运动而形成的散粒噪声称为暗电流噪声,是一种白噪声,其等值电子等于暗电流产生的电子数的平方根.
(3)暗电流非均匀性噪声
由于探测器各像元的暗电流大小不同,形成了暗电流非均匀性噪声.该噪声近似可看作满足泊松分布.
(4)光子响应非均匀性噪声
由于探测器的各像元对光子的响应存在着微小的差别形成了光子响应非均匀性噪声,该噪声与器件的光电信号紧密相关.
(5)读出噪声
电路通道中各种噪声源(读出放大器、可编程增益放大器和模,数转换器)引起的信号电平的随机波动称为读出噪声,在检测弱光信号时此噪声对系统的信噪比影响显著.该噪声可近似看作满足正态分布.
(6)固定模式噪声
由于处理电路和模数转换器在不同列之间存在着失配,会引起列固定模式噪声的问题,突出表现为在图像的垂直方向出现明暗变化的细条纹.
3 试验
3.1 参数设置
以某星敏感器为例,视场:8.9°×8.9°(H×V);模拟星等:0~8.1等星.
3.2 静态星图模拟
在本节主要考虑了噪声与星等的影响.
在本试验中,随机产生一个指向,在该指向下视场中共出现了54颗导航星,不加噪声时产生的星图背景的均值约为0.007,方差约为0.655.叠加噪声后,星图背景的均值为81.097,方差为3.093.
星等与星点的能量E之间的关系如图3所示.图3表明仪器星等越大,星点越暗,能量越低.图4更进一步阐明了这一规律,4(a)中星点能量远高于4(b)中星点能量.
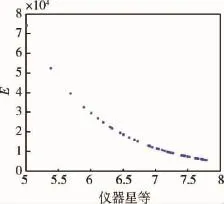
图3 仪器星等与星点能量间的关系Fig.3 Variations of instrumental magnitude and star energy
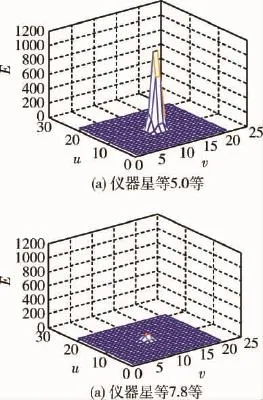
图4 某个仪器星等对应的星点能量分布Fig.4 Star distribution with specific instrumental magnitude
3.3 高机动星图模拟
在本节主要考虑了卫星角速度对星点拖尾的影响.为了与静态模拟生成星图作比较,在本节中亦采用上个指向.当角速度大小为2(°)/s及5(°)/s时,模拟生成星图.由于在z轴方向的角速度,对成像无影响,故在本文考虑了角速度[2 0 0](°)/s、[1.414 1.414 0](°)/s、[5 0 0](°)/s及[3.536 3.536 0](°)/s 4种情况,如图5所示.
图5表明随着角速度的增加星像点拖尾长度增加,当角速度大小为2(°)/s时,拖尾长度为92个像素,当角速度大小为5(°)/s时,拖尾长度约为230个像素.随着角速度的增大,信噪比降低.

图5 不同角速度下模拟的星图及某一星点灰度分布图Fig.5 Star map simulation with different angular rates and the specific star energy distribution
3.4 与真实观星星图比较
将星敏感器放置在观星转台上,角速度设置为[0 1 0](°)/s,采集1 000幅星图,进行星图识别.图像积分时间设置为30 ms.同时采用本文中的星图模拟算法,与采集星图的初始指向相同,生成100幅连续星图.采用相同的星图处理程序处理两个数据集,平均每幅星图中35颗星,结果表明光轴夹角平均值为72″,同一颗恒星能量差平均值为48.7个灰度值.
以某个仪器星等4.73的导航星为例,其能量分布如图6所示.图6表明仿真星图与实拍星图,星点能量相当,但是更为平滑,高斯分布需更精细化处理.

图6 仪器星等4.73等的导航星灰度分布图Fig.6 Energy distribution of the star with magnitude 4.73
4 结论
本文提出了一种动态的全天球星图模拟算法.该算法采用了分区检索导航星的方法,大大提高了检索导航星的速度,从而加快了星敏感器模拟星图的更新频率,满足星模拟器短采样周期的要求.在噪声和环境干扰方面,充分考虑了杂散光干扰和成像器件自身噪声.利用本算法产生的模拟星图,更加真实的模拟了星敏感器在轨工作的状态.本算法的提出有益于星敏感器的杂散光分析、地面性能测试及动态性能验证,对天文导航研究有重要意义.
[1]LIEBE C C.Accuracy performances of star trackers—a tutorial[J].IEEE Transactions on Aerospace and Electronic Systems,2002,38(2):587-589.
[2]KLAUS A,BAUER J,KARNER K,et al.Camera calibration from a single night sky image[C]//The 2004 IEEE Computer Society Conference on Computer Vision and Pattern Recognition.New York:IEEE,2004.
[3]RUFINO G.MOCCIA A.Stellar scene simulation for indoor calibration of modern star trackers[J].Space Technology,2001,21(1-2):41-51.
[4]胡宜宁,巩岩.动态星图显示算法的设计与实现[J].宇航学报,2008,29(3):849-853.
HU Y N,GONG Y.Design and realization of a dynamicdisplay algorithm for star map[J].Journal of Astronautics,2008,29(3):849-853.
[5]徐明庚.卫星姿态动力学与控制(3)[M].北京:中国宇航出版社,2009.
[6]黄博,马杰,田金文.振动模糊星图仿真技术研究[J].计算机与数学工程,2012(4):90-92.
HUANG B,MA J,TIAN J W.Research on simulation of vibration blurred star images[J].Computer and Digital Engineering,2012(4):90-92.
[7]刘海波,宿德志,谭吉春,等.考虑卫星轨道运动和像移影响的星敏感器星图模拟方法[J].宇航学报,2011,32(5):1190-1194.
LIU H B,SU D Z,TAN J C,et al.An approach to star image simulation for star sensor considering satellite orbit motion and effect of image shift[J].Journal of Astronautics,2011,32(5):1190-1194.
[8]王海涌,费峥红,王新龙.基于高斯分布的星像点精确模拟及质心计算[J].光学精密工程,2009(17): 1673-1677.
WANG H Y,FEI Z H,WANG X L.Precise simulation of star spots and centroid calculation based on Gaussian distribution[J].Optics and Precision Engineering,2009(17):1673-1677.
[9]张辉,钟建勇,袁家虎,等.电路噪声对星敏感器星点定位精度的影响[J].光学精密工程,2006(14): 1052-1056.
ZHANG H,ZHONG J Y,YUAN J H,et al.Circuit noise effects on star sensor position accuracy[J].Optics and Precision Engineering,2006(14):1052-1056.
[10]王辰,王宏强,陈明华,等.成像噪声对星敏感器性等灵敏度的影响[J].红外与激光工程,2008,37(5): 858-862.
WANG C,WANG H Q,CHEN M H,et al.Effect of image processor’s noise on magnitude sensitivity of star sensor[J].Infrared and Laser Engineering,2008,37 (5):858-862.
An Approach of Star Image Simulation for Strapdown Star Sensor
LU Rui,WU Yanpeng
(Beijing Institute of Control Engineering,Beijing 100190,China)
The technique of the star map simulation is widely used to test star identification algorithms and the performance of star sensor on the ground.A novel approach of star map simulation is put forward in this paper,considering satellite orbit motion and effect of image shift.The simulation procedure consists of four steps:firstly,searching the navigator stars that appearing in the field of view throughout the whole sky.Dividing index method is proposed to accelerate the selecting velocity.Secondly,the accurate positions of selected guide stars on the image plane of star sensor are derived by constructing a pinhole model.Thirdly,gray values for simulating star image pixels are evaluated according to the 2D Gaussian distribution law.In order to simulate the star image accurately and actually,the image shift should be considered.Finally,noises made by stray light and circuits are added in order to simulate the orbit environment vividly.In a world,the approach proposed here is with the merit of high speed,nice accuracy,and good reality and so on.
star sensor;star map simulation;satellite orbit motion;image shift
V448
A
1674-1579(2016)04-0057-06
10.3969/j.issn.1674-1579.2016.04.011
鹿 瑞(1983—),女,工程师,研究方向计算机视觉、图像处理与成像式敏感器;武延鹏(1977—),男,研究员,研究方向为成像式敏感器.
2016-01-18
