基于局部能量的三次B样条曲线自动光顺算法
2016-04-07章虎冬
章虎冬
(西安邮电大学 理学院,陕西 西安 710121)
基于局部能量的三次B样条曲线自动光顺算法
章虎冬
(西安邮电大学 理学院,陕西 西安 710121)
摘要:给出B样条曲线的一种自动光顺算法,通过求解一个以修改控制顶点为目标函数的优化问题,进而求出光顺后的控制顶点,反复上面的过程,直到最后得到满足约束条件的光顺后的曲线。通过光顺法光顺后的曲线,不仅使曲线的曲率变化比较均匀,而且也使曲线的应变能较小,光顺效果明显。
关键词:B样条曲线;应变能;误差限;光顺准则
0引言
在现代的计算机辅助设计中,由给定的数据点产生一条“光顺的”或者“视觉效果良好”的曲线是一项非常重要的任务。即使运用最有效的B样条曲线,也可能拟合或插值出一条不光顺的曲线。所以对其进行几何处理,使得曲率图变化均匀就显得至关重要。
目前,对曲线的几何处理主要两种方法:一种方法是运用张力样条对曲线进行光顺[1]。另一种方法是交互式光顺:人为观察需要光顺的控制顶点,并通过校正这些点得到光顺后的控制顶点与光顺后的曲线[2-3],但是这需要有经验的专家及大量的人力资源,所以这种交互式的光顺法也有失败的时候[4],而且在交互式光顺中运用较多的是节点的删除和插入算法[5-7]和能量法[8-11],所以不适合于计算机自动辅助设计。给出一种B样条曲线的自动光顺算法就成了计算机辅助几何设计工作者必须解决的问题。本文给出了一种基于优化法的B样条曲线自动光顺算法。以反映光顺性的应变能达到最小作为目标函数,又考虑到误差限,所以,用此算法不仅光顺效果很好而且满足误差要求。
1三次B样条曲线
三次B样条曲线为
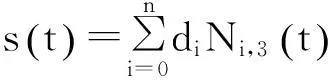
(1)
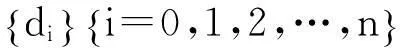
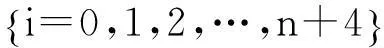
(2)

2光顺准则
对曲线进行光顺,首先必须给出具体的光顺准则,目前在光顺中经常使用的光顺准则有:
Sapidis N等给出的光顺准则1:
在相应于zi值最大的内节点ti(i=4,…,L)处曲线应该被光顺
其中
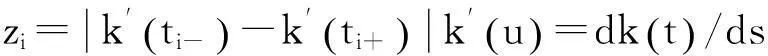
Poliakoff等给出的光顺准则2:
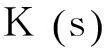
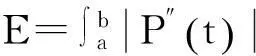
3能量光顺
首先给出一些有用的概念和光顺前后的曲线表示
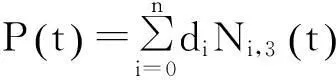
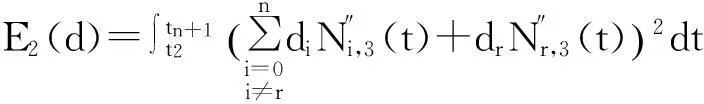
(3)
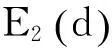
把(3)式代入上式得

(4)
其中权因子
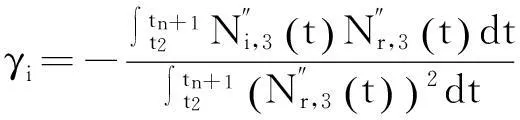
(5)
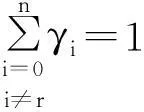
4光顺算法
下面给出光顺算法:
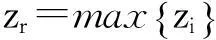
5算例
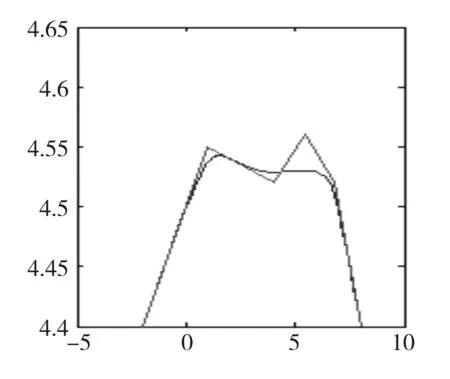
图1 光顺前的曲线
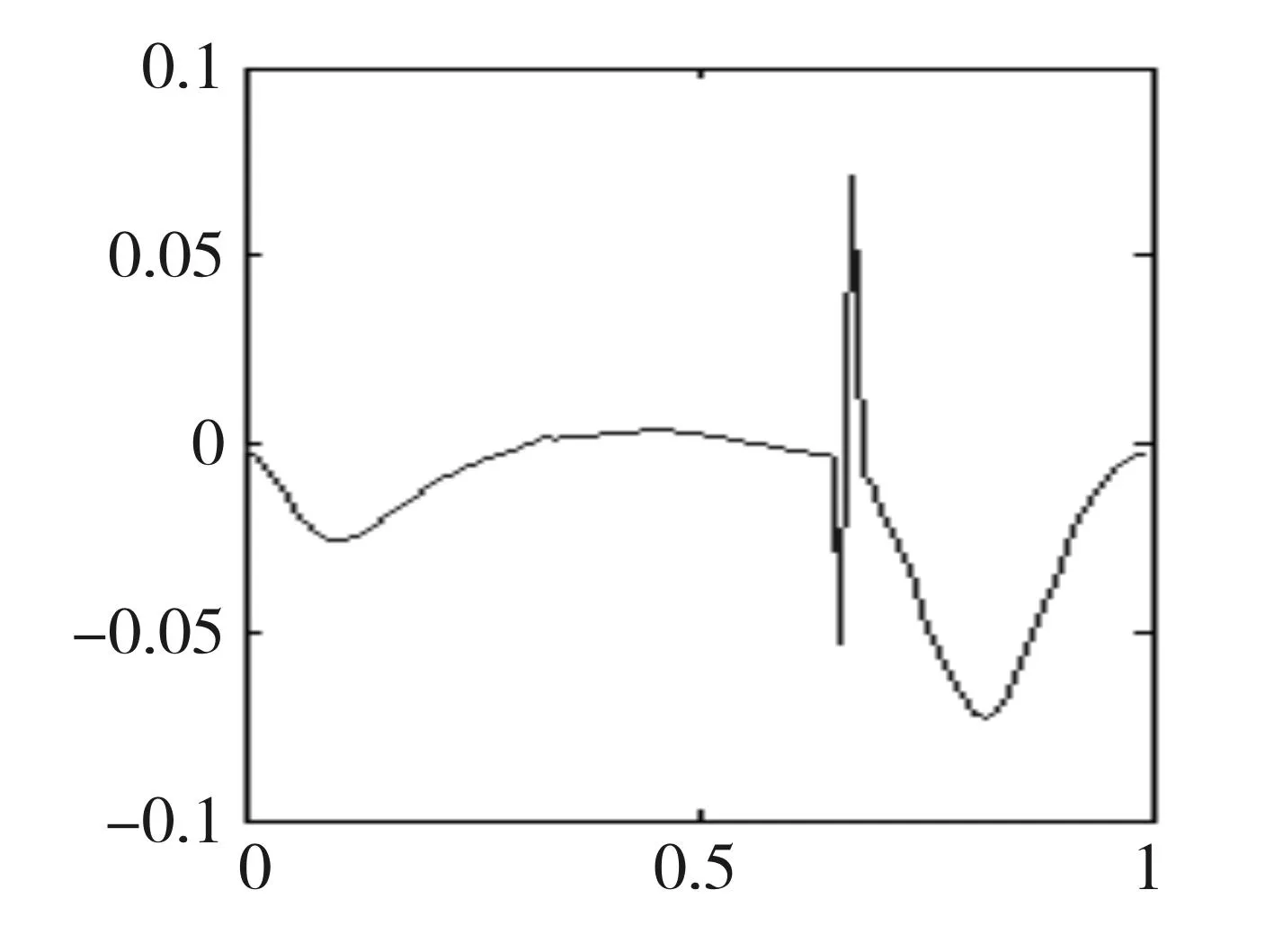
图2 光顺前的曲率图
图1~图4是基于上面的光顺法进行曲线光顺的例子。
图1和图2分别是由所给数据拟合出的曲线以及曲率图,就是我们需要光顺的曲线;图3和图4分别是经过上文的光顺法光顺后的曲线和曲率图。
由曲率图2可以看出,在0.5~1之间频率有一段震荡比较大,这也就说明原曲线这一段上的光顺性比较差。由曲率图4可以看出,在0.5~1之间原来频率震荡比较大的一段现在明显震荡比较小了,这也说明经过本文的光顺法光顺后,得到的曲线光顺性好。并且从图1和图3的比较中可以看出,光顺前后的曲线基本吻合,没有发生较大的变化;从图2和图4的比较中可以看出,曲率变化较原来有了明显的改善,达到了预先的光顺目的。
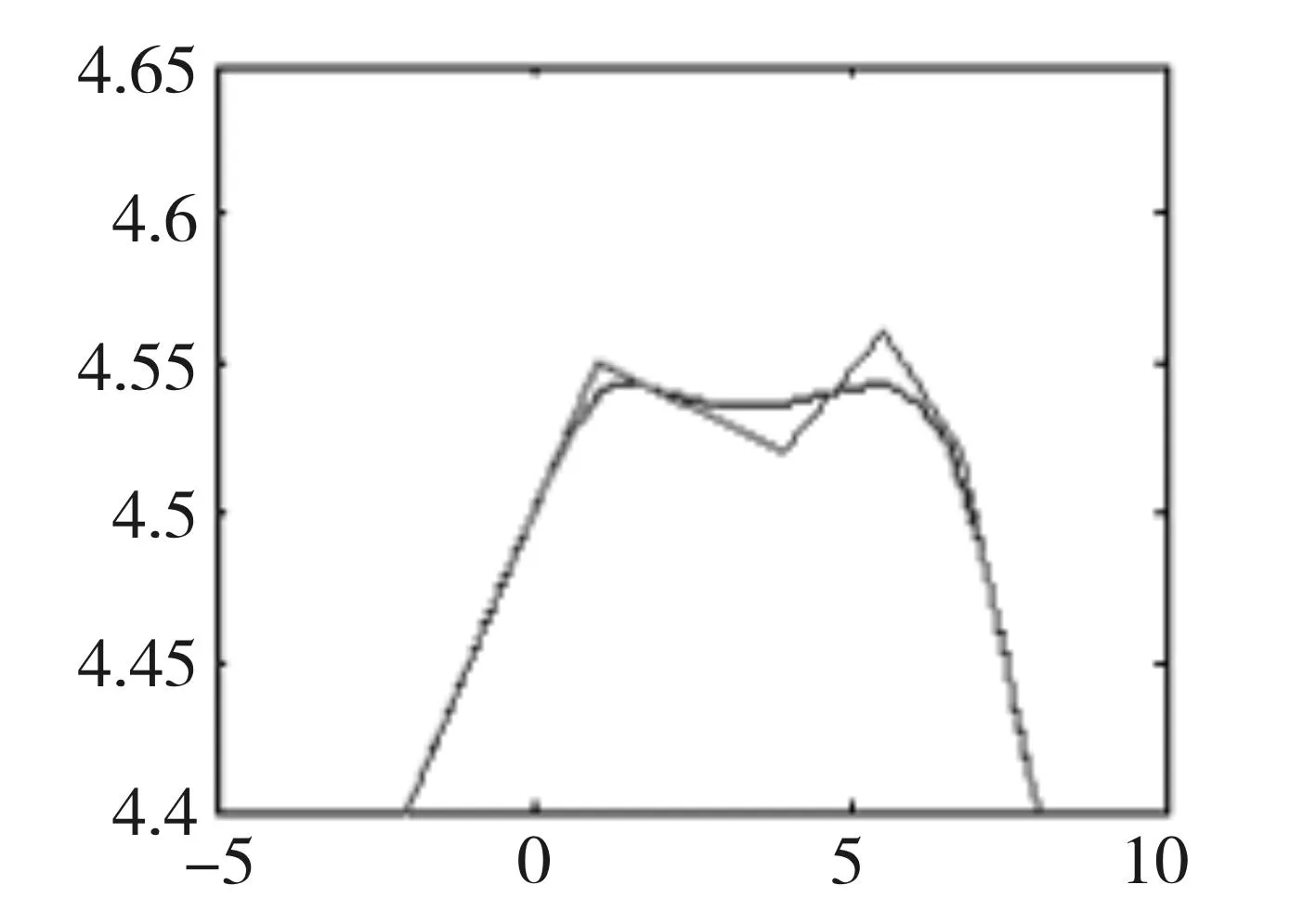
图3 光顺后的曲线
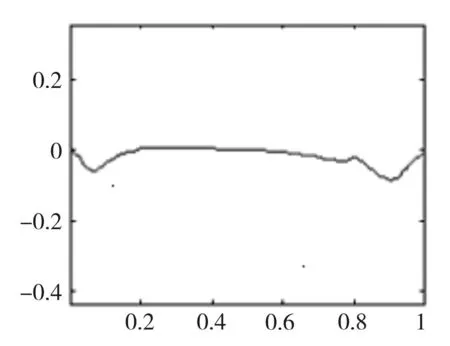
图4 光顺后的曲率图
光顺前型值点的横纵坐标分别为:
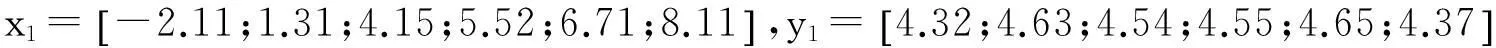
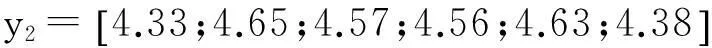
6结论
本文给出了基于局部能量的三次B样条曲线的一种自动光顺算法,首先总结了目前在光顺曲线时所使用的各种光顺准则,并从中选出最适合本文选点修改的光顺准则,通过求解一个以修改控制顶点为目标函数的优化问题,进而求出光顺后的控制顶点,反复上面的过程,直到最后得到满足约束条件的光顺曲线。通过算例可知,在满足控制顶点约束条件下,平面参数三次B样条曲线的光顺效果较好。后期,还可以把这种自动优化光顺算法运用于NURBS曲线的光顺,只是求导比较困难,有待做进一步研究。
参考文献
[1] 朱心雄.自由曲线曲面造型技术[M].北京:科学出版社,2000:348-365.
[2] Kjellander J.Smoothing of cubic parametric splines[J].CAD,1983,15(3):175-179.
[3] Sapidis N,Farin G.Automatic fairing algorithm for B-spline curves[J].CAD,1990,22(2):121-129.
[4] Lee E T Y.Energy,fairness,and a counterexample[J].CAD,1990,22(1):37-40.
[5] 康宝生,赵录刚.平面三次NURBS曲线的自动光顺算法[J].计算机辅助设计与图形学学报,2002,14(3):225-227.
[6] 满家巨,胡事民,雍俊海,等.B-样条曲线的节点去除与光顺[J].软件学报,2001,12(1):143-147.
[7] Tiller W.Knot-removal algorithms for NURBS curves and surfaces[J].CAD,1992,24(8):445-453.
[8] Nowacki H,LIU D Y,LU X M.Fairing Bézier curves with constraints[J].CAGD,1990(7):43-55.
[9] ZHANG C M,ZHANG P F,CHENG F H.Fairingspline curves and surfaces by minimizing energy[J].CAD,2001,33(11):913-923.
[10] 李安平,蒋大为.三次均匀有理B样条曲线的权因子优化光顺算法[J].计算机辅助设计与图形学学报,1997,9(6):562-567.
[11] Hildebrandt K,Polthier K.Constraint-baseed fairing of surface meshes[C]//Proceedings of the Fifth Eurographics Symposium on Geometry Processing.Spain:Barcelona,2007.
[责任编辑、校对:李 琳] 第34卷第1期2016年1月西安航空学院学报JournalofXi'anAeronauticalUniversityVol.34No.1Jan.2016
An Automatic Faring Algorithm of Cubic B-spline Curves Based on Local Energy
ZHANGHu-dong
(School of Science,Xi'an University of Post and Telecommunications,Xi'an 710121,China)
Abstract:Local Energy Fairing of parametric cubic B-spline curves is presented in this paper.Firstly,we summarize all kinds of fairing criteria for curves fairing and select most suitable fairing criteria for the proposed algorithm.Secondly,by solving an optimization problem of having constraint condition,we obtain the fairing control points.Lastly,fairing curve is got by repeating process above.Fairing curves are acquired.Through this paper,the curve of the ray becomes smooth.Not only the curvature of the curve is more uniform,but also the strain of the curve can be smaller,so the effect is obvious.
Key words:B-spline curves;strain energy;distance tolerance;fairing criteria
中图分类号:O241.5;TP391
文献标识码:A
文章编号:1008-9233(2016)01-0079-03
作者简介:章虎冬(1979-),男,内蒙古呼和浩特人,讲师,从事计算机辅助几何设计研究。
基金项目:西安邮电大学校青年基金资助项目(106-205010228);陕西省教育厅科研项目(14JK1655)
收稿日期:2015-11-25
