基于Mathematica的顾及地形的开采沉陷三维可视化

蔡音飞，李晓静，邓伟男

(1.太原理工大学 矿业工程学院，山西 太原 030024；2.洛林大学 南锡高等矿业学院 ，法国 南锡 54000；

3.山西农业大学 资源与环境学院，山西 太谷 030801；4.天地科技股份有限公司 开采设计事业部，北京 100013)



基于Mathematica的顾及地形的开采沉陷三维可视化

蔡音飞1，2，李晓静3，邓伟男4

(1.太原理工大学 矿业工程学院，山西 太原 030024；2.洛林大学 南锡高等矿业学院 ，法国 南锡 54000；

3.山西农业大学 资源与环境学院，山西 太谷 030801；4.天地科技股份有限公司 开采设计事业部，北京 100013)

[摘要]利用Mathematica软件，考虑原始地表数据和由顾及地形的开采沉陷预计方法计算得到的沉陷数据，实现了原始地表、沉陷和受沉陷影响的地表的三维可视化。顾及地表的开采沉陷预计需使用2个偏斜影响函数分别描述单元开采的下沉和水平移动，进而按经典方法进行积分。应用Mathematica的插值函数和绘图函数，绘制所需的各种三维图形，可直观反映沉陷后的地表形态。

[关键词]Mathematica；地形影响；影响函数法；插值；三维可视化

采矿引起的地表沉陷对矿区的土地、建筑、道路等的功能和安全造成了不同程度的影响[1-2]。很多矿区的地表是非水平的，结合地表形态因素，以三维图示的方法表现沉陷和沉陷后的地形，可以更直观、准确地对沉陷区土地、地物进行损毁分析。单独沉陷数据的三维显示在很多研究中都有报告，但只能表现矿区地表为水平面时的开采沉陷状况，而无法顾及矿区原有的地表特征，因此尚不能够真实反映开采后的地表情况[3]。有些研究工作已实现了沉陷影响下的矿区地形三维可视化，或采用DEM法编程实现[4-5]，或使用GIS软件[6-11]、南方CASS[12]等配合沉陷数据实现。这些方法虽然在原始地形上叠加了沉陷数据以实现受开采影响的地形三维显示，但是在计算沉陷时均未能考虑原始的非水平地表对沉陷的影响，并且沉陷预计与其后的三维显示成图均不是在同一软件中实现的，操作和数据转换有诸多不便。

本文使用考虑地形变化的开采沉陷预计程序，计算非水平地表条件下的沉陷，然后与原始地形数据相叠加，获得受开采影响后的地表数据，并实现三维显示，为矿山开采前的设计、规划，开采后的评估、复垦提供可视化支持和依据。

本文沉陷预计和数据叠加均在Mathematica中完成。Mathematica是由沃尔夫勒姆研究公司开发的一款被广泛使用的科学计算软件，拥有强大的数值计算和符号运算能力，是科学计算的完全集成环境、交互式的问题解决系统[13]，其提供的高等数学函数可以直接用于本研究的开采沉陷预计程序的开发，极大地简化了编程过程；其提供的插值函数和绘图函数也为三维显示输出提供了便利。

1顾及地表形态的开采沉陷预计方法

理论上，水平地表条件下，沉陷与地形叠加后的形态与仅考虑沉陷不叠加地表的形态是完全一致的。本文研究对象是非水平地表条件下的开采沉陷三维可视化，首先需将地表变化的影响纳入开采沉陷预计计算中。

本文使用的开采沉陷预计程序是基于影响函数法[14-15]，在Mathematica环境下开发的。笔者在文献[16]中详细说明了考虑地形因素的开采沉陷预计程序的基本原理，即采用偏斜正态分布的概率密度函数，如式(1)、式(2)所示。作为影响函数，用以描述单元开采在地表倾向方向上的下沉和水平移动，按照经典影响函数法，采用积分的方法求取任意地表点的移动变形量。

(1)

(2)

(3)

(4)

式(1)～式(4)中：G(x)为正态分布(高斯分布)的概率密度函数；erfc(x)为高斯误差函数，用于偏斜G(x)；G(x)和erfc(x)的积即为偏斜正太分布的概率密度函数；ifv(x)为下沉在地表倾向方向上的影响函数；ifh(x)为水平移动在地表倾向方向上的影响函数；sm，α，μ，σ为地形相关的修正系数，对于ifv(x)，ifh(x)其取值是不同的，其中，sm用于修正单元开采下沉和水平移动的数值大小、α用于修正他们的偏斜度、μ用于修正他们在地表倾向方向上相对于开采单元的位置、σ用于修正他们的影响范围。

相对于经典影响函数法，本方法最主要的特点为：

(1)使用了2个影响函数分别描述单元开采的下沉和水平移动。研究发现，在非水平地表条件下，水平移动不再和倾斜(下沉的导数)相似，即水平移动无法再由下沉计算，因此需要定义2个影响函数。其他的地表移动变形量(倾斜、水平变形、曲率)仍可用经典方法计算。

(2)地表高程数据需要作为已知数据输入计算。上述2个影响函数中的地形影响修正系数都可以表示为地表相对矿体高程和地表倾角的函数。实际上，地表倾角也可以由地表高程求导得到，所以对于本方法而言，只有地表高程数据(更准确地说是地表相对矿体高程数据)是较经典方法新增的输入数据。

通过使用按照上文原理开发的开采沉陷预计程序，可以在沉陷计算中考虑非水平地表的影响，相对于原来的预计方法，能够得到相对更精确的预计结果。

2受沉陷影响的地表三维可视化

Mathematica提供了一个插值函数(Interpolation)，适用于任意维数数据的插值(本文涉及的地形数据、沉陷数据均为三维)，插值的方法可选择样条曲线(Spline)插值法或埃尔米特(Hermite)插值法，得到的结果是一个函数，可以和其他任何数学函数一样使用。应用该插值函数，配合Mathematica提供的三维绘图函数(Plot3D)可以方便地绘制地表和沉陷的三维图形，包括受沉陷影响后的地表形态。

本节结合法国洛林地区某矿实例[16]进行说明。洛林曾是法国主要的矿产区，当地大多采用房柱法开采，很多矿山在停采多年后面临矿柱逐渐失稳，地表沉陷频发的问题。本文研究的2个开采区块近年来有失稳的迹象，其拐点坐标见表1(文中图表所用坐标系均为RGF93 / Lambert-93，为便于表述，所有平面坐标均统一减去一定值，经过现场实测，这2个区块造成的最大地表下沉值约为0.5m，影响角约为30°。

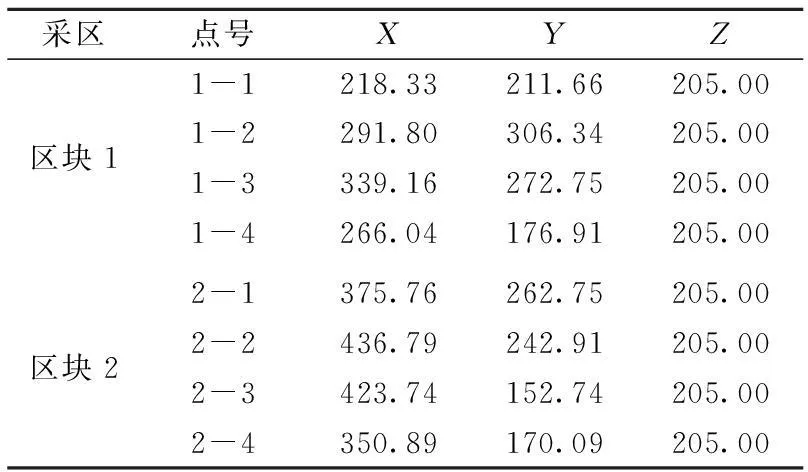
表1　失稳的开采区块拐点坐标

2.1原始地表

任何途径获得的原始地表数据均可以用三维数组表示：surfdata = {{x1，y1，z1}，{x2，y2，z2}，…,{xn，yn，zn}}，其中x,y为地表点的平面坐标，z为对应点的高程。开采区块上方的若干离散地表点高程数据已知，这些点的位置绘于图1(图中，每个点相连的竖线底端位置是该点的平面位置，竖线长度为相对最低点的高程)，其高程约介于+330m到+390m之间，最大高差约60m。

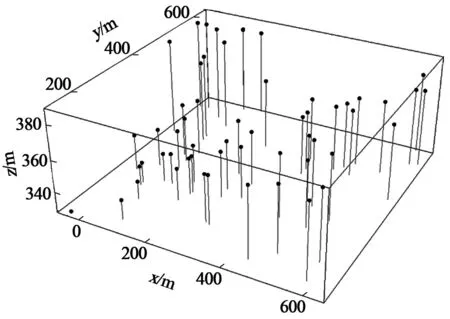
图1　有高程数据的地表点位置示意

以x，y为自变量，使用样条曲线插值法，地表点高程z的插值函数(此处记为SurfZ[x，y])可以用以下命令在Mathematica中求取：

SurfZ[x，y]= Interpolation [surfdata，Method → “Spline”，InterpolationOrder → 1]

“InterpolationOrder → 1”表示不进行平滑处理，该值越大，插值后的函数图形越光滑。

在Mathematica中使用Plot3D函数(仅需提供三维函数作为输入数据即可输出图形)，可将原始地表函数SurfZ(x,y)输出为三维图形：

Plot3D [SurfZ[x，y]，{x，0，600}，{y，0，600}，UserSettings]

“{x，0，600}”和“{y，0，600}”用于指定输出范围；“UserSettings”是图形显示相关附加设置的集合(如：颜色、字体、坐标轴、比例、观察点等)。

输出的原始地表三维图见图2。需要说明的是(对图3，图4亦同，不再赘述)：本文将地表的颜色设置为高程的函数并用灰度区分，实际上，Mathematica提供了很多颜色函数，支持彩色输出；观察点位置可以设置，或者直接在程序中拖动图形进行三维旋转；传统的平面等值线、色晕图与三维输出方法类似，因非本文内容，在此不展开说明；图中地表的网格线是为了更清楚地显示，实际操作中并不需要求网格点处的函数值；为了便于将开采区块与地表等一起显示，图中开采区块的高程是经过调整的，各点实际高程以表1为准。

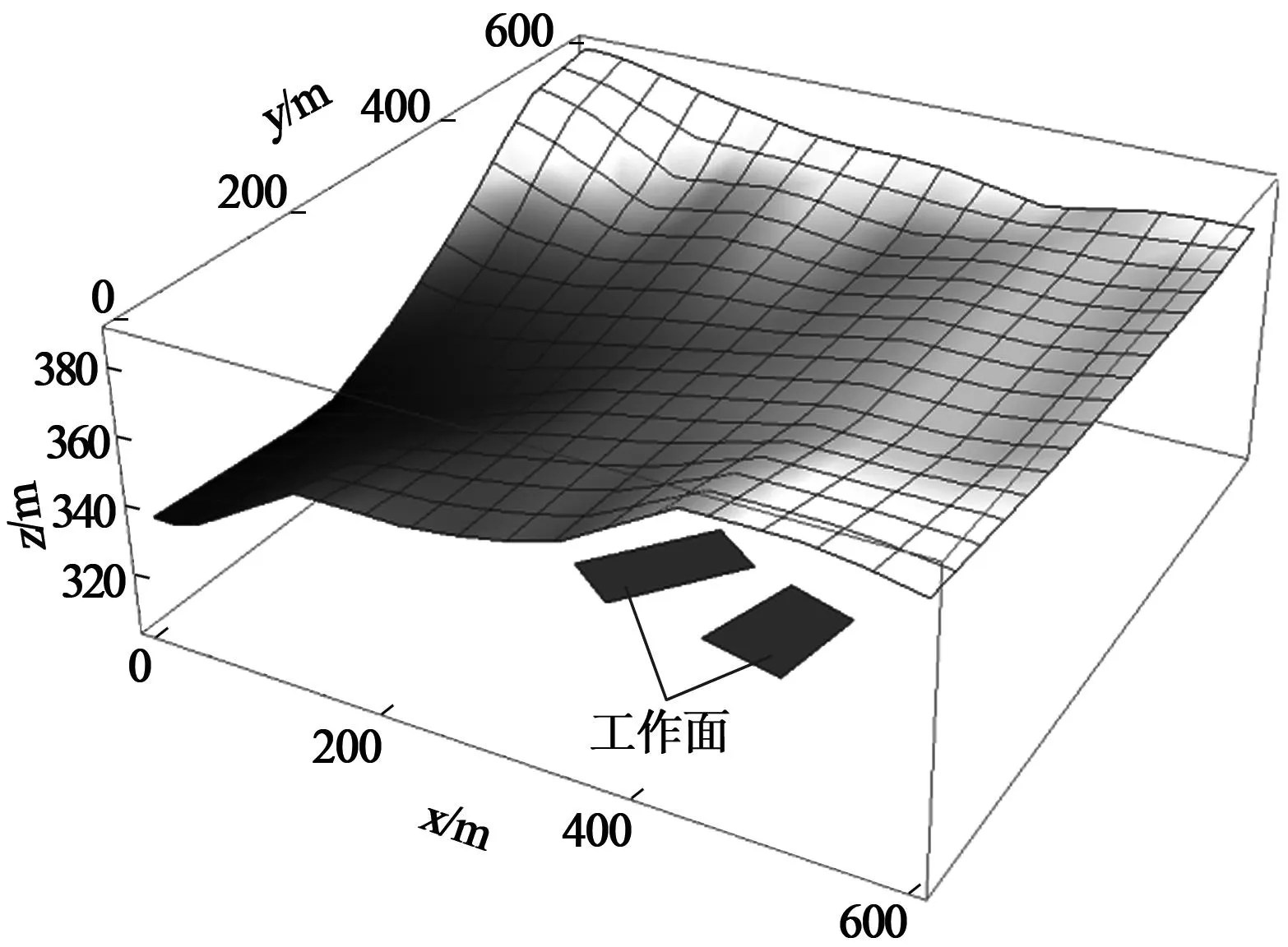
图2　原始地表三维示意

2.2开采沉陷计算

应用上文考虑地表形态的开采沉陷预计方法(已在Mathematica中编程实现)，计算由开采区块1，2矿柱失稳造成的沉陷，获得下沉、水平移动数据。与处理地表数据类似，可以在Mathematica下，用插值函数算得下沉、x方向水平移动、y方向水平移动的函数，记为SubsV[x，y]、SubsHx[x，y]、SubsHy[x，y]。以下沉为例，其三维图如图3所示。

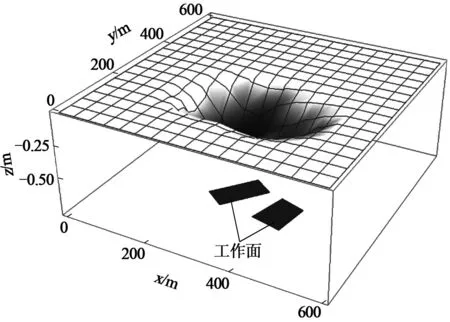
图3　下沉三维示意

在Mathematica中，插值函数与一般初等函数一样，可以通过赋予自变量值得到函数值；也可以进行四则运算、求导、积分等。因此用下沉、水平移动的函数求偏导可以求得相应方向上的倾斜、水平变形、曲率。

2.3受沉陷影响的地表

在求取受下沉影响的地表时，无需如传统用列表的方法一样考虑数据点位置对应问题，直接将原始地表函数SurfZ[x，y]与下沉函数SubsV[x，y]相加(下沉记为负值)，即可得到考虑下沉的地表函数。水平移动与原始地表叠加的方法类似，但稍微复杂，需将SubsHx[x，y]，SubsHy[x，y]与对应的平面坐标相加。由于沉陷量(下沉0.5m左右)与地表高差(60m左右)相比较小，按照实际沉陷量与地表叠加后与原始地表对比不明显。本文将沉陷量放大20倍后，叠加沉陷(下沉和水平移动)的地表三维示意见图4。

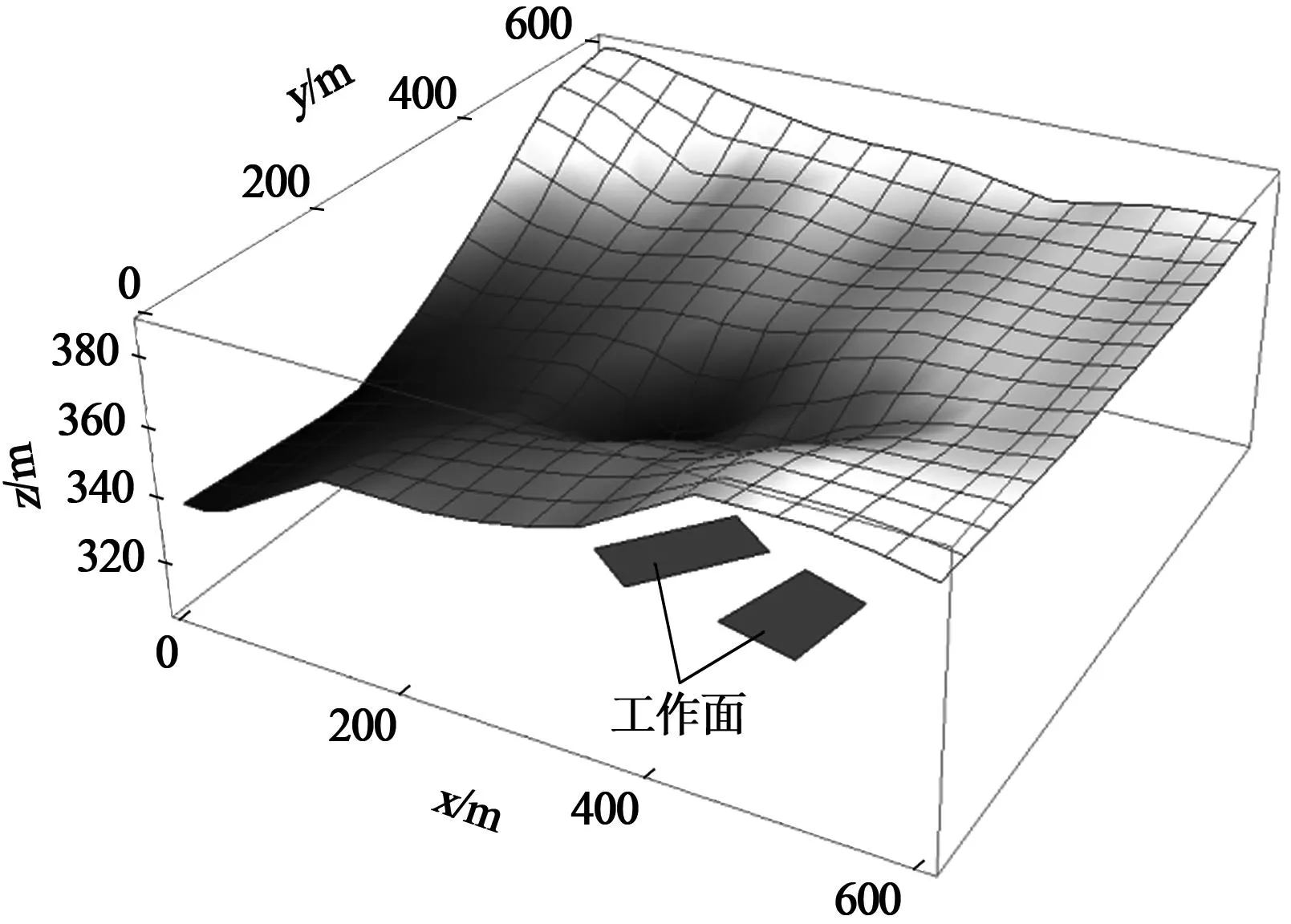
图4　受沉陷影响的地表三维示意

2.4数据、图形输出

Mathematica可以将数据以各种自定义的列表形式输出到Text或者Excel等常用软件，与其他程序配合使用无障碍；图形也可以以图片格式(常用均可)或者矢量格式(包括eps，svg，dxf等)输出，便于进一步处理。

本文为说明Mathematica在图形显示方面的便利和优越性，所有图片均仅在Mathematica中通过调整显示参数(UserSettings)直接生成，未在其他软件中处理。

3结论

(1)使用考虑地形影响的开采沉陷叠加原始地表，实现了受沉陷影响的地表三维可视化。

(2)沉陷计算和受沉陷影响的地表三维可视化均在同一个软件中实现，操作更方便，无需考虑数据转换问题。

(3)使用Mathematica提供的高等数学函数、插值函数、绘图函数，编程更简练，效率更高。

[参考文献]

[1]邓伟男，张华兴，徐乃忠.开采损害影响范围的多方法比较鉴定模式及其应用[J].煤矿开采，2013，18(2)：105-107.

[2]Li Xiao-jing，Hu Zhen-qi，Li Shuang-cheng，et al.Anomalies ofmountainousmining paddy in western China[J].Soil and Tillage Research，2015(145)：10-19.

[3]肖武，胡振琪，李太启.采区地表动态沉陷模拟与复垦耕地率分析[J].煤炭科学技术，2013，41(8)：126-128.

[4]柴华彬，邹友峰，刘景艳.DTM在开采沉陷可视化预计中的应用[J].辽宁工程技术大学学报(自然科学版)，2004，23(2)：171-174.

[5]陈秋计，胡振琪，刘昌华，等.DEM在矿区土地复垦中的应用研究[J].金属矿山，2006 (2)：67-68.

[6]戴华阳.基于倾角变化的开采沉陷模型及其GIS可视化应用研究[J].岩石力学与工程学报，2002，21(1)：148-148.

[7]刘立民，刘汉龙，连传杰.基于GIS的矿山塌陷损害评价系统及可视化方法[J].防灾减灾工程学报，2003，23(1)：69-73.

[8]孟峰.矿区地表沉陷预计三维可视化研究[J].陕西煤炭，2006 (2)：10-12.

[9]王京卫，栾红，汝续伟.顾及矿区地貌特征的开采沉陷三维可视化实现方法[J].山东科技大学学报(自然科学版)，2007，26(1)：8-11.

[10]Dai Hua-yang，Ren Li-yan，Wang meng，et al.Water distribution extracted frommining subsidence area using Kriging interpolation algorithm[J].Transactions of Nonferrousmetals Society of China，2011(21)：723-726.

[11]卢志刚，刘兴权，唐义宏.基于GIS和FLAC3D矿山地表沉陷可视化[J].现代矿业，2012 (11)：44-46.

[12]易四海，戴华阳，廉旭刚，等.顾及地表沉陷的矿区地貌可视化实现方法[J].湖南科技大学学报(自然科学版)，2008，23(4)：81-84.

[13]Wolfram Stephen.Themathematica book[M].Wolframmedia，Incorporated，1996.

[14]National Coal Board.Subsidence engineers’handbook[M]. London：National Coal Board，1975.

[15]何国清，杨伦，凌赓娣，等.矿山开采沉陷学[M].徐州：中国矿业大学出版社，1991.

[16]Cai Yin-fei，Verdel Thierry，Deck Olivier.On the topography influence on subsidence due to horizontal undergroundmining using the influence functionmethod[J].Computers and Geotechnics，2014，61(6)：328-340.

[责任编辑：徐乃忠]

3-D Visualization of Mining Subsidence Considering Terrain Based on Mathematica

CAI Yin-fei1，2,LI Xiao-jing3,DENG Wei-nan4

(1.College of Mining Engineering,Taiyuan University of Technology,Taiyuan 030024,China;2.Nancy Higher Mining Institute,Lorraine University,Nancy 54000,France;3.College of Resources and Environment,Shanxi Agricultral University,Taigu 030801;4.Coal Mining & Designing Department,Tiandi Science & Technology Co.,Ltd.,Beijing 100013,China)

Abstract:Applying mathematica software,3-d visualization of original surface,subsidence,and surface influenced by subsidence was realized with original surface data and subsidence data calculated by mining subsidence prediction method. The mining subsidence prediction considering terrain need to use deflection influence functions respectively describing sink and horizontal displacement of elements,and farther finish integral with classic method. Using interpolation function and drawing function,various 3-d graphs were drawn which could directly reflect surface configuration after subsidence.

Key words:Mathematica;terrain influence;influence function method;interpolation;3-d visualization

[中图分类号]TD327

[文献标识码]A

[文章编号]1006-6225(2016)01-0080-04

[作者简介]蔡音飞(1983-)，男，浙江嘉兴人，博士，主要研究方向为“三下”采煤技术及其理论的研究与应用。

[收稿日期]2015-07-19

[DOI]10.13532/j.cnki.cn11-3677/td.2016.01.022

[引用格式]蔡音飞，李晓静，邓伟男.基于Mathematica的顾及地形的开采沉陷三维可视化[J].煤矿开采，2016，21(1)：80-83.