平面稀疏阵列天线的约束优化设计*
2016-04-06赵宏伟李维梅西安空间无线电技术研究所西安710100
刘 恒,赵宏伟,李维梅,刘 波(西安空间无线电技术研究所,西安710100)
平面稀疏阵列天线的约束优化设计*
刘 恒**,赵宏伟,李维梅,刘 波
(西安空间无线电技术研究所,西安710100)
**通信作者:liuheng@ mail. nankai. edu. cn Corresponding author:liuheng@ mail. nankai. edu. cn
摘 要:针对有阵元数和阵列口径约束的矩形平面稀疏阵天线的综合问题,提出了一种基于整数编码的差分进化算法。该方法以每个阵元的栅格位置编号作为设计变量,使阵列的稀疏率满足约束条件,避免了优化过程中的不可行解,还减少了优化变量的个数。为了加速优化过程,采用快速傅里叶变化计算阵列的方向图。以改善阵列峰值副瓣电平为目的进行仿真试验,结果表明:优化后的稀疏天线阵峰值旁瓣电平比现有方法相比改善了1. 2~1. 7 dB,且具有收敛性和稳定性好的优点。
关键词:阵列天线;稀疏阵列;差分进化算法;快速傅里叶变换;约束优化
1 引 言
稀疏相控阵天线是指从规则排布的均匀相控阵中按照一定的比例剔除掉部分阵元[1],或者将这些阵元连接到匹配负载上,这样既可以减少阵列天线成本和重量,还可以获得与满阵排布相当的窄波束。当阵元均匀激励时,稀疏阵列天线可以获得比满阵布置更低的副瓣电平。由于稀疏阵列天线不需要幅相调整的放大器和移相器等器件,具有结构简单和成本低等优点,已成功应用在抗环境干扰的卫星接收天线、高频地面雷达和射电天线学中的干涉阵等领域。
针对稀疏阵列天线优化设计的问题,已经出现多种综合方法,如密度加权法[2]、动态规划法[3]和分数阶勒让德变换法[4]等。随着计算机技术的发展,高效的全局优化随机优化算法已成研究热点,有遗传算法[5-6]、粒子群算法[7]、差分进化算法[8]、蚁群算法[9]和迭代傅里叶算法[10]等各种优化算法的混合算法[11-12]。由于稀疏阵列的设计是一个0-1规划问题,在这些文献中大多采用二进制编码[5-9],其中“0”和“1”分别代表相应的栅格位置上是否放置天线阵元。二进制编码的方式虽然直观,但是在优化过程中阵列的稀疏率容易遭到破坏,对于有稀疏率约束的稀疏阵列优化,只有蚁群算法和迭代傅里叶算法可以精确地控制处于“开”状态的阵元,其他的随机进化算法个体的稀疏率在每次操作中是变化的,只有极少数满足约束,从而产生大量不可行解,这严重地影响算法的搜索性能。
差分进化算法(Differential Evolution,DE)是由Storn和Price两位学者提出的[13],由于其高效快速、随机并行搜索方式,且操作简单、搜索能力强,已经广泛应用于阵列天线综合等电磁优化问题[14]。杨仕文[15]应用DE算法在时间调制天线阵列和幅度激励的方向图综合,取得了比遗传算法更快的收敛速度。本文提出一种基于整数编码DE算法,采用整数编码方式使得优化过程中阵列的稀疏率保持恒定,为加速优化过程,采用快速傅里叶变换(Fast Fourier Transform,FFT)计算阵列方向图。以降低阵列天线的峰值副瓣电平的实验进行仿真,结果证明了本文方法在工程应用中的有效性和可行性。
2 矩形平面稀疏阵列天线模型
设稀疏优化布阵模型为图1所示,阵列在x轴方向有M行栅格,行间距为dx;在y轴方向有N列栅格,列间距为dy。所以,阵元均为理想点源,此时阵列的方向图为
式中:Amn是第(m,n)个阵元的激励幅度,对于稀疏阵,当Amn=1,表示该阵元被保留;若Amn=0,则该阵元被稀疏;k=2π/λ,λ为工作波长;u=sinθcosφ;v= sinθsinφ,θ、φ分别为球坐标系下的俯仰角和方位角。
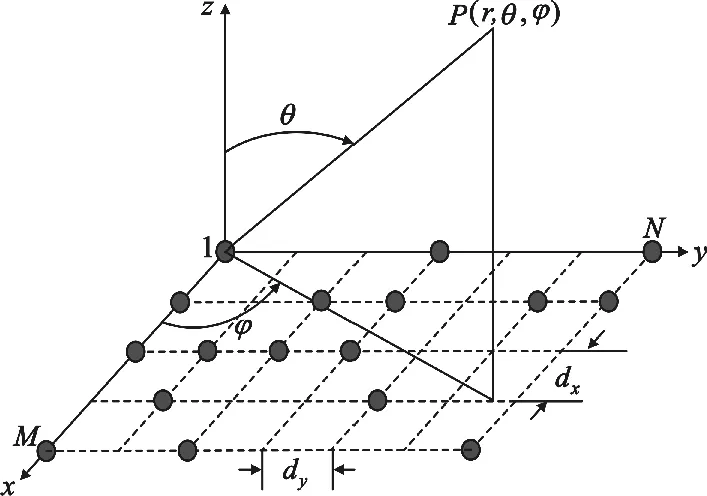
图1 矩形平面稀疏阵列模型Fig. 1 Model of rectangular thinned planar array
令p=Mkdxu/2π+1,q=Nkdyv/2π+1,则式(1)变换为
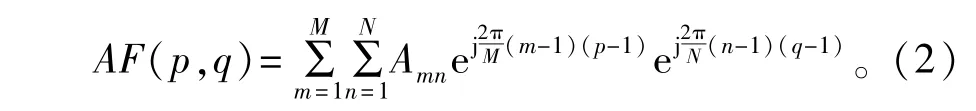
由式(2)可以看出阵因子AF(u,v)与阵元激励A之间存在FFT关系:AF(u,v)= MN×IFFT(A),这样根据具体的问题,将(θ,φ)域的方向图特性映射到(p,q)域中进行计算。对于约束的阵元数为T,求解阵元位置,使稀疏阵的峰值副瓣电平(Peak Sidelobe Level,PSLL)最低。为了保持阵列孔径,约束矩形边界的角阵元不被稀疏,得到的最优化模型为
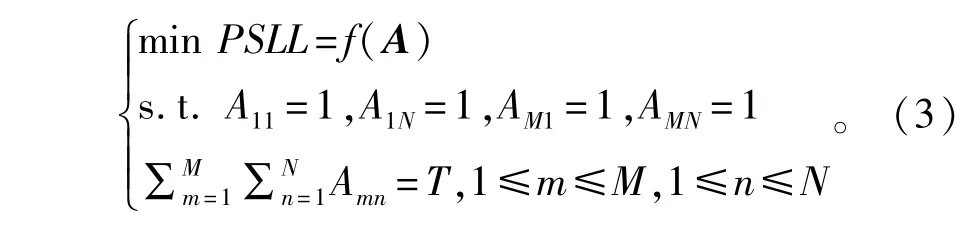
以改善稀疏阵的PSLL为优化目标,则适应度函数定义为

式中:S表示方向图的副瓣区域;FFmax是主瓣点电平值。
3 算法描述
对于栅格间距规则的稀疏阵列,阵元都分布在规则的栅格点位置上,对这些栅格点进行编号就可以采用整数编码的方式来描述个体,不仅减少了优化变量的个数,还可以精准地控制阵元数。考虑到阵列孔径的约束,矩形阵列的4个角分别放置阵元,则剩下需要优化的阵元数为D=T-4,可以供放置阵元的栅格点数为MN-4,对这些栅格点进行编号[1#,2#,…,(MN-4)#],则把式(3)需要优化的A转换为D个阵元所对应的栅格点编号作为设计变量。
定义D维空间的向量x=sort[x1,x2,…,xD]为闭区间[0,MN-T]内的生成的随机数并按从小到大的顺序排列,在此基础上构造一个目标向量x对应的阵元位置编号向量:
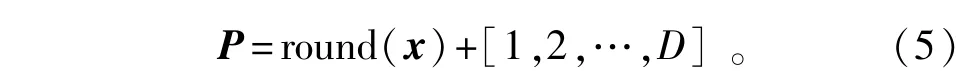
式中:round(·)为四舍五入取整,则第i(i = 1,2, …,D)个阵元对应在的栅格点编号为round(xi)+i; x的不同取值分别对应稀疏阵激励A的不同分布。
容易证明采用x作为个体的编码,由个体x采用式(5)生成的阵元位置编号序列满足阵列孔径阵元数的约束。为了减小优化变量的数量,根据稀疏率的大小来判断是对“阵元”的栅格位置还是对“空”栅格的位置进行编码。当稀疏率小于50%时选择有阵元的栅格作为变量,反之则选择空的栅格位置作为变量。因此,本文采用整数编码的DE算法对有稀疏率约束的稀疏阵列的优化操作具体如下。
(1)种群初始化:根据变量范围[0,MN-T],在上下边界空间尽可能地均匀生成种群,对每个个体按从小到大的顺序排列并四舍五入取整。
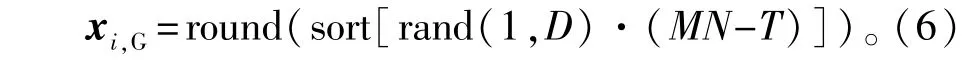
式中:rand(1,D)为D维的[0,1]区间上的随机数。
(2)变异:随机选取的3个不同目标向量,生成变异向量vi,G= round ( sort [ xr1,G+ F·( xr2,G-xr3,G)]),差分因子F∈[0,2]。
(3)交叉:对变异个体vi,G和xi,G进行交叉操作,产生新的试验向量ui,G=sort(u1i,G,u2i,G,…,uDi,G)。

式中:CR∈[0,1]是交叉概率;k任意随机整数,以确保至少有一维vi,G贡献给实验向量ui,G。
(4)解码并计算适应度函数:对目标向量和试验向量按式(5)解码得到阵元的位置,并根据式(4)计算适应度。
(5)选择:目标向量与试验向量进行竞争,适应度值更优的个体作为进入下一轮进化。
(6)判断是否满足迭代次数上限或收敛准则,未满足,转到第2步;
(7)输出最好个体对应的阵列结构,优化结束。
4 稀疏阵列天线的优化实例
应用本文提出的算法对矩形平面阵列的栅格点数为20×10放置108个阵元,稀疏率为54%的阵列进行优化,阵元均为理想点源,阵元间距dx= dy= λ/2。由于稀疏率大于50%,我们选择“空”栅格位置编码作为优化变量。为了使结果具有的对比性, IFFT采用与文献[10]中相等的采样点数K = 256,迭代进化次数G=1 000。DE算法的种群数为200,策略参数采用DE/ rand/1/ bin,差分因子F=0. 5,交叉概率为0. 9。为了体现本文方法的稳健性,独立运行10次仿真程序。
4. 1 对称矩形平面稀疏阵列优化结果
由于矩形平面阵列具有对称结构,只需要优化1/4阵元分布,然后利用对称性映射出整个阵列的阵元分布。采用本文提出的方法对栅格点为20×10稀疏率为54%的对称平面稀疏阵优化的收敛曲线图2所示,最好优化结果PSLL=-19. 88 dB,与文献[10]对相同的对称阵列采用IFT算法相比,改善了1. 2 dB;最差结果相比也改善了0. 26 dB。
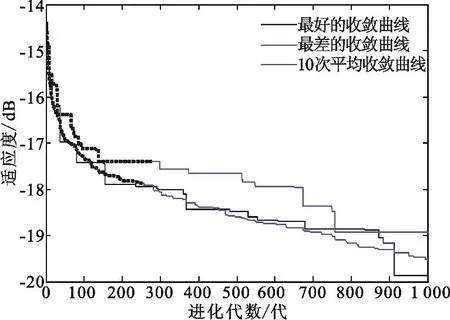
图2 对称优化收敛曲线Fig. 2 Convergence of symmetric optimization
表1给出了本文方法与现有方法优化结果对比,包括PSLL、主瓣3 dB波束宽度和方向性系数D(文献[6]中没有给出阵列分布图,无法计算出相应的D)。从表1中可以看出本文方法与现有方法相比,PSLL得到很大改善,在主瓣3 dB波束宽度同等情况下,增益得到了改善。
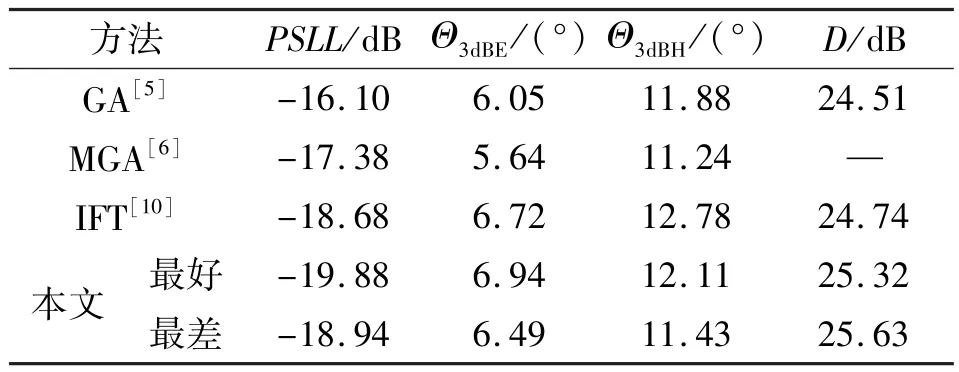
表1 本文方法与现有方法对称优化结果对比Tal. 1 Symmetric optimization result comparison between DE and GA
图3给出了最好稀疏阵的阵元分布图,实心圆表示该栅格有阵元,空心圆表示该栅格无阵元。阵列中心阵元密集,边缘阵元排布比较稀疏,符合稀疏阵列优化的一般规律,最好稀疏阵对应的远场方向图如图4所示。

图3 最好对称矩形稀疏阵列阵元分布图Fig. 3 Symmetric elements distribution in aperture
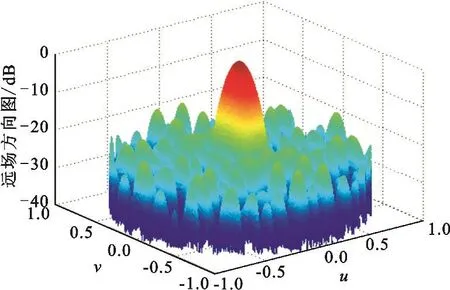
图4 对称阵列的远场方向图Fig. 4 Far field pattern of the symmetric array
4. 2 非对称矩形平面稀疏阵列优化结果
本节同样对栅格点为20×10稀疏率为54%的对称平面稀疏阵优化。由于非对称优化具有更多的设计自由度,相对而言可以得到比对称优化更优的结果。10次独立优化的收敛曲线图5所示,最好优化结果PSLL = -21. 39 dB,与文献[10]采用IFT算法非对称优化相比,改善了1. 7 dB;最差结果相比也改善了0. 54 dB。
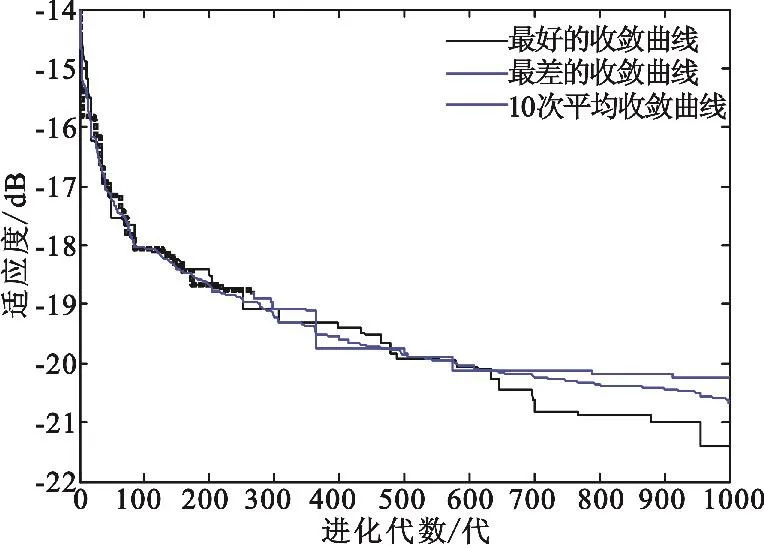
图5 非对称优化收敛曲线Fig. 5 Convergence of asymmetric optimization
表2给出了本文方法与IFT方法优化结果对比,可以看出本文方法与IFT相比,PSLL得到了改善,且主瓣3 dB波束宽度和增益也得到了改善。
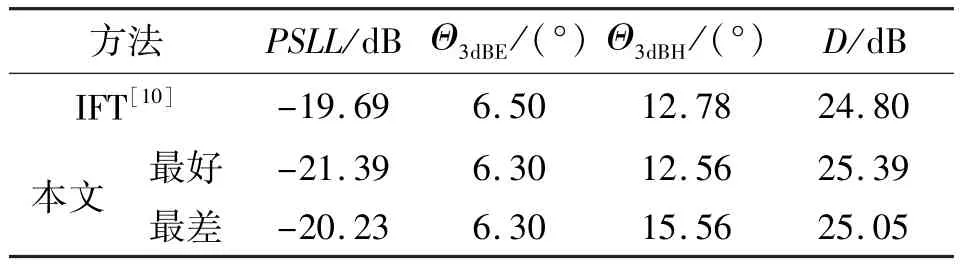
表2 本文方法与现有方法非对称对比Tab. 2 Asymmetric optimization result comparison between DE and GA
图6给出了最好稀疏阵的阵元分布图,实心圆表示该栅格有阵元,空心圆表示该栅格无阵元,最好稀疏阵对应的远场方向图如图7所示。

图6 最好非对称矩形稀疏阵列阵元分布图Fig. 6 Asymmetric elements distribution in aperture
图7 非对称阵列的远场方向图Fig. 7 Far field pattern of the asymmetric array
5 结束语
随机进化算法在优化的稀疏阵列时,个体的稀疏率容易遭到破坏,从而产生大量不满足稀疏率的不可行解,严重影响算法的搜索性能。为了保证阵列的稀疏率满足约束,本文提出了一种基于整数编码的DE算法。该方法对阵列的栅格点进行编号,采用整数编码的方式来描述个体,不仅减少了优化变量的个数,还可以精准的控制阵元数。利用整数编码的DE算法对矩形稀疏阵列天线进行优化处理,为了快速计算六边形阵列的辐射场,利用FFT快速的计算阵列的辐射方向图。以改善阵列的峰值副瓣电平为目,取得了比已有算法更优的结果。这种整数编码的方式可以应用于DE算法以外的其他算法,并可以用于其他类型的阵列形式的设计优化。
参考文献:
[1] KEIZER W P M N. Synthesis of thinned planar circular and square arrays using density tapering[J]. IEEE Transactions on Antennas and Propagation,2014,62(4):1555-1563.
[2] STEINBERG B. The peak sidelobe of the phased array having randomly located elements[J]. IEEE Transactions on Antennas and Propagation,1972,20(4):621-634.
[3] SKOLNIK M I,NEMHAUSER G,SHERMAN J W. Dynamic programming applied to unequally spaced arrays [J]. IEEE Transactions on Antennas and Propagation, 1964,12(1):35-43.
[4] KUMAR B P, BRANNER G R. Design of unequally spaced arrays for performance improvement[J]. IEEE Transactions on Antennas and Propagation, 1999, 47 (3):511-523.
[5] HAUPT R L. Thinned arrays using genetic algorithms [J] . IEEE Transactions on Antennas and Propagation, 1994,42(7):993- 999.
[6] 彭祥龙.用遗传算法优化任意稀布率的平面阵列[J].电讯技术,2007,47(3):153-158.
PENG Xianglong. Using genetic algorithm to optimize thinned planar arrays with arbitrary thinned factor[J]. Telecommunication Engineering,2007,47(3):153-158. (in Chinese)
[7] 史东湖,习靖,周志伟.对称平面稀疏阵列阵形优化方法研究[J].飞行器测控学报,2013,32(4):302-305.
SHI Donghu,XI Jing,ZHOU Zhiwei. Research on optimization method of symmetric thinned planararray[J]. Journal of Spacecraft TT&C Technology,2013,32(4):302-305. (in Chinese)
[8] ZHANG L,JIAO Y C,WENG Z B,et al. Design of planar thinned arrays using a Boolean differential evolution algorithm [ J]. IET Microwaves, Antennas & Propagation, 2010,4(12):2172-2178.
[9] OSCAR Q T,EVA R I. Ant colony optimization in thinned array synthesis with minimum sidelobe level[J]. IEEE Antennas Wireless Propagation Letters,2006(5):349-352.
[10] 曾伟一,梁颖,黄伟.基于迭代FFT算法的平面稀疏阵列优化方法[J].电讯技术,2011,51(11):99-102.
ZENG Weiyi,LIANG Ying,HUANG Wei. An optimum method for thinned planar array based on iterative FFT algorithm[J]. Telecommunication Engineering,2011,51 (11):99-102. (in Chinese)
[11] YEPES L F,CONVARRUBIAS D H,ALONSO M A,et al. Hybrid sparse linear array synthesis applied to phased antenna arrays[J]. IEEE Antenna and Wireless Propagation Letters,2014(13):185-188.
[12] BUCCI O M,PERNA S,PINCHERA D. Synthesis of isophoric sparse array allowing zoomable beams and arbitrary coverage in satellite communications[J]. IEEE Transactions on Antennas and Propagation, 2015, 63 (4):1445-1457.
[13] STORN R,PRICE K. Differential evolution-a simple and efficient heuristic for global optimization over continuous spaces[J]. Journal of Global Optimization,1997 (11):341-359.
[14] GOUDOS S K,SAHALOS J N. Pareto optimization microwave filter design using multiobjective differential evolution[J]. IEEE Transactions on Antennas and Propagation,2010,58(1):132-142.
[15] YANG S,GAN Y B,QING A. Sideband suppression in time modulated linear arrays by the differential evolution algorithm[J]. IEEE Antennas Wireless Propagation Letters,2002(1):173-175.

刘 恒(1986—),男,湖南衡阳人,2012年于中国空间技术研究院获硕士学位,现为博士研究生,主要研究方向为阵列天线优化与设计;
LIU Heng was born in Hengyang, Hunan Province,in 1986. He received the M. S. degree from China Academy of Space Technology in 2012. He is currently working toward the Ph. D. degree. His research concerns array antenna design and optimization.
Email:linheng@ mail. nankai. edu. cn
赵宏伟(1982—),男,山东潍坊人,2008年于东北大学获硕士学位,现为博士研究生,主要研究方向为DOA估计与智能算法;
ZHAO Hongwei was born in Weifang,Shandong Province, in 1982. He received the M. S. degree from Northeastern University in 2008. He is currently working toward the Ph. D. degree. His research concerns DOA estimation and smart method.
李维梅(1986—),女,甘肃陇西人,博士研究生,主要研究方向为射频子系统关键技术;
LI Weimei was born in Longxi,Gansu Province,in 1986. She is currently working toward the Ph. D. degree. Her research concerns key technology of RF system.
刘 波(1963—),男,湖南汉寿人,研究员、博士生导师,主要研究方向为卫星总体设计。
LIU Bo was born in Hanshou,Hunan Province,in 1963. He is now a senior engineer of professor and also the Ph. D. supervisor. His research concerns satellite system design.
Constraint Optimization of Planar Thinned Array Antenna
LIU Heng,ZHAO Hongwei,LI Weimei,LIU Bo
(Xi'an Institute of Space Radio Technology,Xi'an 710100,China)
Abstract:For the rectangular planar thinned array with the design constraint of the filling factor,a differential evolution algorithm based on integer code is proposed to reduce the peak sidelobe level(PSLL). In order to avoid the infeasible solution during the optimization,the position number of grid is set as the optimization variable on the premise of the condition that the thinned ratio constraint is satisfied and the variables are reduced. Meanwhile,a fast Fourier transform(FFT) is employed to speed up the calculation of pattern. Then the proposed method is applied to design a low side lobe rectangular planar thinned array. The simulated results show that the PSLL is reduced by 1. 2~1. 7 dB and good convergence and stability can be achieved.
Key words:array antenna;thinned array;differential evolution algorithm;fast Fourier transform;constraint optimization
doi:10. 3969/ j. issn. 1001-893x. 2016. 02. 011引用格式:钟亚君,吴次南,刘泽文.用于UHF频段的RFID波束扫描阵列天线设计[J].电讯技术,2016,56(2):171-175. [ZHONG Yajun,WU Cinan,LIU Zewen. Design of an RFID beam scanning array antenna for UHF band[J]. Telecommunication Engineering,2016,56(2):171-175. ]
作者简介:
中图分类号:TN821
文献标志码:A
文章编号:1001-893X(2016)02-0166-05
*收稿日期:2015-08-28;修回日期:2015-11-27 Received date:2015-08-28;Revised date:2015-11-27
