一种高稳定度帆板驱动系统的摩擦参数辨识*

程俊波，张 强，虎 刚，于国庆，陆栋宁

(1.北京控制工程研究所，北京100190;2.中国长城工业总公司，北京100054)

一种高稳定度帆板驱动系统的摩擦参数辨识*

程俊波1，张 强1，虎 刚2，于国庆1，陆栋宁1

(1.北京控制工程研究所，北京100190;2.中国长城工业总公司，北京100054)

为了减少帆板驱动机构(SADA)对太阳帆板的激励作用和降低摩擦的影响，以永磁同步电机作为驱动源，提出了一种基于LuGre模型的摩擦参数辨识和补偿方法.为了能够准确的进行摩擦参数的试验辨识，设计了SADA系统摩擦力矩测试平台两者相结合进行了试验辨识，并将试验辨识所得到的摩擦模型参数代入SADA驱动系统模型中.通过仿真和试验表明:试验辨识较准确，且摩擦补偿后的SADA系统消除了正弦跟踪中速度过零时的波形畸变现象，能够有效改善SADA系统的动态性能.

帆板驱动机构;永磁同步电机;摩擦;参数辨识;粒子群

0 引 言

太阳帆板驱动机构(SADA)是太阳帆板与卫星本体之间的机电接口，连接太阳帆板与卫星本体的同时，驱动帆板相对本体按照一定规律转动，并且将太阳电池获得的电能通过导电环向本体电源系统传输［1-2］.为了降低每个导电环组件的传输功率，SADA所设置的导电环数量很多，由此产生了很大的摩擦力矩，且帆板转速极低，其低速摩擦特性尤为复杂，存在预滑动、摩擦滞后、动静摩擦转换、Stribeck摩擦、摩擦记忆效应等非线性现象.这些非线性特性不但限制了高性能驱动策略和方法在SADA系统中的应用，严重时还会影响帆板驱动的平稳性，导致卫星姿态指向精度和稳定度下降.

因此，为提高卫星姿态控制精度与稳定度，需对太阳帆板驱动机构摩擦特性开展测试研究，并选用较适合的摩擦模型，进行参数辨识，获得较精确摩擦模型.然而，由于摩擦模型是复杂非线性函数，对于辨识参数而言，按常规方法进行参数辨识比较困难.因此，需要利用智能算法的非线性全局搜索能力对摩擦模型参数进行辨识.文献［3］利用速度和行程位置信号作为输入信号，用遗传算法对该LuGre模型的动静态参数进行辨识.文献［4］利用电机匀速和自由减速两种状态的电流和转速变化离线辨识摩擦模型的静态参数，但没有对动态参数进行辨识.文献［5］通过精确测量摩擦预滑阶段的摩擦力和角位移，采用频域辨识方法获取动态参数.

本文采用扰动力矩较少的永磁同步电机作为驱动源，并建立了SADA系统的控制模型.然后，以速度为输入，摩擦力矩为输出，采用粒子群算法对系统的摩擦模型进行了参数辨识.为了能够准确的实现摩擦参数的试验辨识，设计了SADA系统摩擦力矩测试平台，解决了极低转速下常规方法无法对摩擦力矩精确测量的难题.然后，以永磁同步电机作为驱动源对刚性负载进行驱动.最后，通过仿真与试验对比，验证了系统摩擦参数辨识的准确性.

1 SADA驱动系统建模

SADA驱动系统包含SADA和太阳帆板两部分，SADA系统示意图如图1所示.

图1 太阳帆板驱动系统的示意图Fig.1 The schematic diagram of the solar array drive system

SADA驱动系统的一般驱动原理是:当太阳敏感器发现太阳帆板法线方向与太阳光线之间的夹角误差大于设定的阈值时，将启动太阳的捕获模式，此时运行速率较高，约0.24～0.6(°)/s.当帆板基本实现对日定向时，SADA进入跟踪模式，此时帆板以轨道角速度连续转动，对于地球静止轨道卫星约为360(°)/天，而太阳同步轨道卫星约为0.06(°)/s.

由于永磁同步电机驱动由正弦波电流驱动，虽仍然存在一定的干扰力矩，但仍比步进电机小得多.因此，为了降低驱动系统的扰动力矩，本文采用永磁同步电机作为帆板驱动机构的驱动源，其采用永磁同步电机的SADA驱动系统的原理图如图2所示.

图2 SADA驱动系统的机电一体化模型示意图Fig.2 The schematic diagram of the solar array drive system

1.1 永磁同步电机的模型

由于SADA驱动系统是在极低速的情况下进行驱动，因此，本文采用基于转子磁场定向的永磁同步电机矢量控制方案对SADA进行驱动.

若认为永磁同步电机转子永磁磁链ψr不变，永磁同步电机定子绕组电压方程可以写为:

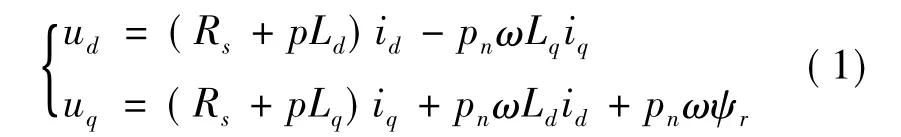
式中:ud、uq分别表示定子侧的d和q轴电压;id、iq分别表示定子侧的d和q轴电流;Rs表示定子侧电枢电阻;ω表示转子机械角频率;p为微分算子;Ld、Lq表示定子侧的d、q轴电感;ψr表示转子永磁体在定子绕组中产生的磁链，即转子永磁磁链;pn表示转子极对数.

对式(1)进行整理，将其表达成以d、q轴电流为状态变量的状态方程形式:

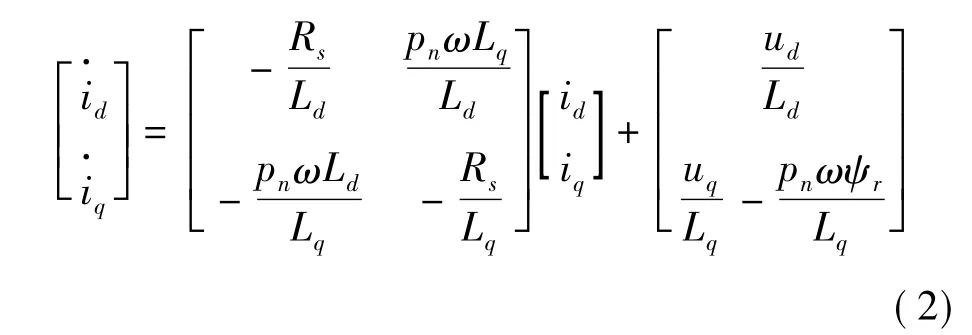
电磁转矩表达式为:

式中Te表示电机电磁转矩.注:本文采用的表面式永磁同步电机d、q轴电感相等.

1.2 太阳帆板驱动模型

根据帆板的力学特性，应用拉格朗日法可以得到帆板驱动系统的动力学方程如下:

式中:Te表示电机电磁转矩;Tf表示摩擦力矩;J表示挠性负载转动惯量;Fi(i=1，2，…N)表示帆板转动与挠性的耦合系数;θ为挠性负载转过的机械角度;η∈RN为挠性模态变量;K∈RN×N为模态刚度; D∈RN×N为模态阻尼.

1.3 摩擦模型

由于帆板驱动系统中存在比较复杂的摩擦非线性现象，故采用经典的摩擦模型，如Coulomb摩擦+粘性摩擦模型，并不能真实地反映摩擦现象的动态过程.而LuGre摩擦模型是一个较为完善的动态摩擦模型，该模型考虑了2个接触面之间弹性刚毛的平均偏移来表征摩擦的动态行为，精确地描述了摩擦过程复杂的静态和动态特性［6］.LuGre模型数学描述如下:

式中，ω分别为转速，z为粘滞状态下运动表面间的相对变形量，Fc为库仑摩擦力矩，Fs为最大静摩擦力矩，ωs为临界Stribeck转速，即摩擦力矩负斜度与正斜度相交点的速度，fv为粘性摩擦阻尼系数，σ0为移动前微观变形量z的刚度，σ1为的动态阻尼.由此可以看出，摩擦模型可由4个静态参数(Fc，Fs，ωs，fv)和2个动态参数(σ0，σ1)描述.

2 SADA系统的摩擦模型参数辨识

LuGre模型是带微分方程的复杂非线性函数，对于辨识参数而言，按常规方法选取的评价函数容易存在多个局部极值点，而传统参数辨识方法大多数基于梯度估计，容易陷入局部极值，很难准确得到LuGre模型的全部参数.

粒子群算法［7］:

粒子群优化算法(PSO)是一种实现简单、全局搜索能力强且性能优越的启发式搜索技术，在面对非线性优化问题时有较大的优势.

PSO初始化为一群随机粒子(随机解)，通过迭代找到最优解.在每次迭代中，粒子通过跟踪两个“极值”来更新自己.第一个就是粒子本身所找到的最优解，称为个体极值，记为Pdi;另一个极值是整个种群目前找到的最优解.该极值是全局极值，记为Pdg.找到这两个最优值时，粒子更新自己的速度和新的位置，表达式为

式中:vdi为第i个粒子的速度;Xdi出为第i个粒子的位置;c1和c2为非负常数.称为学习因子;r1和r2为介于［0，1］之间的随机数.每一维粒子的速度都会被限制在一个最大速度口vmax;如果某一维更新后的速度超过用户设定的vmax，那么这一维的速度就被设定为vmax，即vdi∈［－vmax，vmax］.

2.1 粒子群算法参数辨识原理

用粒子群算法进行系统辨识有两种方案:一种是根据先验知识来确定模型结构，再用粒子群算法来优化模型参数;另一种是用粒子群算法优选几种通过经验估计的结构，并同时估计其参数，本文选用第一种方案对摩擦参数进行辨识.其辨识原理如图3所示.

图3 摩擦辨识原理图Fig.3 The schematic diagram of friction parameter identification

如图3所示，u(k)为系统输入信号;y(k)为系统输出实际观测值;ye(k)为估计模型计算值;输出误差e(k)=y(k)－ye(k).

2.2 动静摩擦参数辨识

上述模型的动静态参数可分两步进行辨识:首先，通过多组匀速运动试验数据预估静态参数范围，采用粒子群算法辨识静态参数;然后，通过预滑移阶段的试验数据预估动态参数范围，采用粒子群算法辨识动态参数.

(a)静态辨识

式中，fv为粘性摩擦系数，Fc为库仑摩擦力矩，Fm为最大静摩擦力矩，ωc为Stribeck特征速度，ω为转子的转速，Ff为摩擦力.

然后，应用粒子群算法优化获得式(7)中的4个静态参数.

其中:

定义辨识误差为

Ff由式(7)确定.

取目标函数

则辨识问题即为最小化目标函数Js.

(b)动态参数辨识

由于LuGre摩擦模型的内部状态变量z不可测量，模型的动态参数的辨识相对困难，因此，可在预滑阶段近似按以下公式计算σ00和σ10的值［8］:

式中:J为总转动惯量，ΔT、Δθ为预滑移阶段力矩和转角的变化量.与辨识静态参数类似，根据σ00和σ10的值预估动态参数的搜索范围，由粒子群算法进行优化.设待辨识参数，定义辨识误差为

式中:θ(ti)为实际系统在ti时刻的输出;θ1(xd，ti)为由辨识参数组成的模型系统在ti时刻的输出.由此定义目标函数如下:

式中c1，c2为权系数.辨识目标为极小化Jd.

3 测试平台的设计

由于太阳帆板驱动机构的工作在极低转速区间，摩擦力矩呈现动摩擦和静摩擦耦合特性，而常规的阻力矩测量手段难以稳定模拟在力矩作用下的极低转速的稳定转动.因此，为了准确测量导电环在极低转速下的摩擦力矩波动，本文采用大惯量的气浮台，降低转动过程中的角加速度，使测力台能够获得较多的测量数据，提高测量精度.

为了拟合出速度-摩擦曲线，本文采用陀螺仪置于气浮台转盘处，实现对SADA旋转速度的测量.然后，将测力台所测的摩擦力矩数据与陀螺仪所测速度的数据进行拟合，得出导电环的速度-摩擦力矩曲线.其SADA摩擦力矩测试系统示意图以及实物图如图4和图5所示.其中，为了排除气浮台电机和SADA电机对测试的干扰，所有工况都要求处于不通电状态.

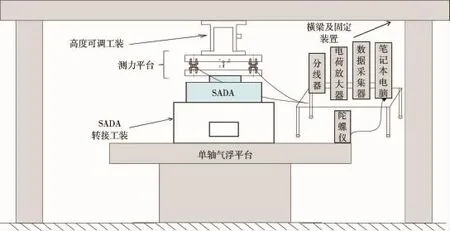
图4 SADA摩擦力矩测试系统示意图Fig.4 The schematic diagram of SADA friction test system

图5 SADA摩擦力矩测试平台实物图Fig.5 SADA friction torque test platform

4 仿真与试验

4.1 参数辨识仿真

本文通过限定粒子群规模、粒子维数及最大迭代次数来完成SADA系统静态及动态摩擦参数的辨识，以最优个体为辨识输出.

对于系统的 LuGre模型静态参数，种群大小M=40，最大迭代次数T=200，Fc∈［0，1］，Fm∈［0，1］，ωc∈［0，0.5］，fv∈［0，1］，辨识结果如表1中所示.

对于LuGre模型动态参数，种群大小M=50，最大迭代次数T=100，σ0∈［0，2 000］，σ1∈［0，10］，辨识结果如表1中所示.由表1可看出，此方法所辨识的LuGre摩擦模型参数比较精确的.

4.2 参数辨识试验验证

考虑加入一个过零点的正弦测试信号，幅值为0.6(°)/s，频率为0.85 Hz，验证试验辨识摩擦模型的准确性.将辨识到的LuGre摩擦力矩模型代入带有刚性负载SADA系统模型中进行仿真.然后，将得到的型仿真的结果与实测速度曲线进行对比分析，其对比结果如图6所示.仿真与试验对比分析表明，试验辨识的模型参数可以很好地复现实测SADA系统的速度曲线，较为准确地预测SADA系统过零的转速波动.

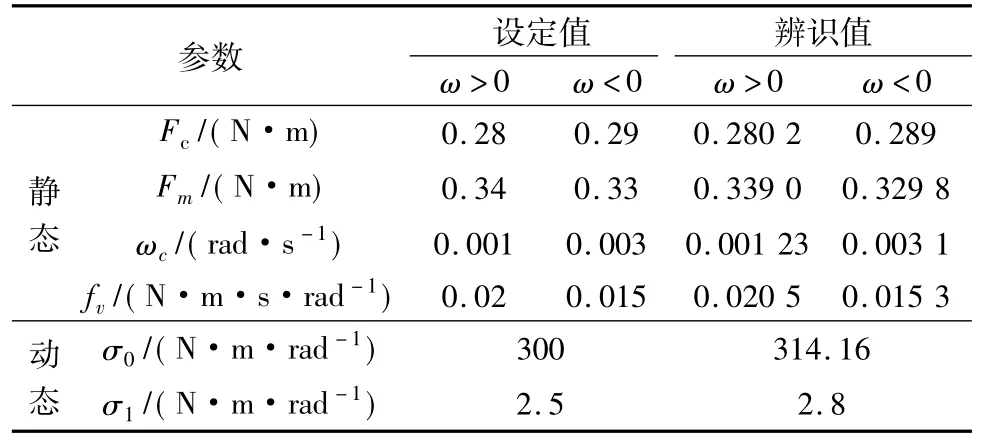
表1 摩擦参数辨识结果Tab.1 Identification result of friction parameters

图6 实测速度曲线与模型仿真速度曲线对比Fig.6 The comparison between test curve and simulation curve

4.3 基于辨识摩擦模型的摩擦补偿

为了验证摩擦力矩的动态补偿效果，将辨识的摩擦模型对带有刚性负载的SADA系统进行摩擦补偿，其试验得到的速度曲线和误差曲线如图7和图8所示.从图中可以看出，采用摩擦补偿后，其速度曲线更加平滑，基本消除了正弦跟踪中速度过零时的波形畸变现象.因此，此摩擦补偿方法能够有效的克服SADA系统的摩擦爬行现象，改善了系统的跟踪性能.

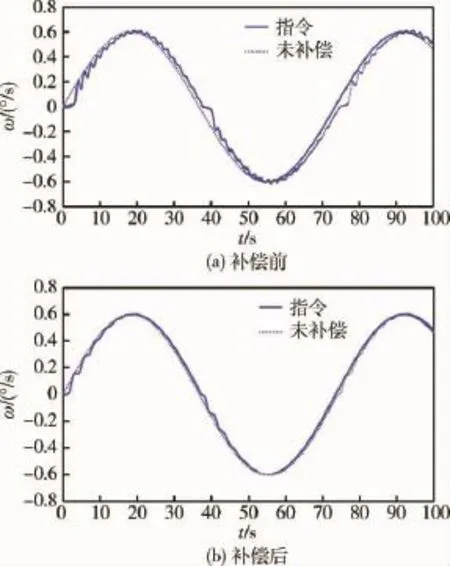
图7 摩擦补偿前后速度曲线对比图Fig.7 The comparison speed curve between without friction compensation and with friction compensation

5 结 论

本文采用扰动力矩较少的永磁同步电机作为驱动源，降低了电机对帆板的激励，并建立了SADA系统的闭环控制模型.然后，以速度为输入，摩擦力矩为输出，并采用粒子群算法对系统的LuGre摩擦模型进行了辨识.为了能够准确的进行摩擦参数的试验辨识，设计了SADA系统摩擦力矩测试平台，实现了极低转速下摩擦力矩的精确测量.然后，将辨识得到的摩擦参数带入带有刚性负载SADA系统中进行仿真和实验验证.通过仿真和试验验证得出以下结论:

(1)带有辨识摩擦参数的模型仿真速度曲线与实测速度曲线的现象基本一致，证明试验辨识得到的摩擦参数的是较准确的.

(2)通过摩擦补偿后SADA系统基本消除了正弦跟踪中速度过零时的波形畸变现象，能够有效改善SADA系统的动态性能.

为了更好的表现摩擦补偿方法的有效性，本文仅针对带刚性负载的SADA系统的摩擦参数进行了辨识与补偿，而下一步将进行带有挠性负载的SADA系统的摩擦补偿的试验验证工作.

图8 摩擦补偿前后的误差曲线对比图Fig.8 The comparison speed error curve between without friction compensation and with friction compensation

［1］高星.卫星姿态动力学与控制(4)［M］.北京:中国宇航出版社，2006.

［2］Patrick S，Christine E.Hiigh performance stepper motor for space mechanisms［R］.NASA，N95-27271，1995.

［3］向红标，裘祖荣，李醒飞，等.精密实验平台的非线性摩擦建模与补偿［J］.光学精密工程，2010，18(5): 1119-1127.XIANG H B，QIU Z R，LI X F，et al.Nonlinear friction modeling and compensation of high-precision experimental platforms［J］.Optics And Precision Engineering，2010，18(5):1119-1127.

［4］胡浩军，毛耀，马佳光，等.稳定转台摩擦参数的测量及其对稳定精度的影响［J］.光电工程，2007，34(5): 5-9.HU H J，MAO Y，MA JG.Stabilized turntable friction parameters measurement and the effect on the stabilized accuracy［J］.Opto-Electronic Engineering，2007，34 (5):5-9.

［5］李拥军.光电跟踪系统低速平稳性技术研究［D］.成都:中国科学院光电技术研究所，2009.

［6］CANUDAS de wit C，OLSSON H，ASTROM K J，et al.A new model for control of systems with friction［J］.IEEE Trans Automation Control，1995，40(3):419-425.

［7］KENNEDY J，EBERHART R C.Particle swarm optimization［C］//Proceedings of IEEE International Conference on Neural Networks，IV.Piscataway.New York: IEEE，1995:1942-1928.

［8］JOH an K，CANU das C.Revisiting the LuGre friction model［J］.Control Systems Magazine，IEEE，2008，12(1):101-114.

Friction Parameter Identification for High Stability SADA

CHENG Junbo1，ZHANG Qiang1，HU Gang2，YU Guoqing1，LU Dongning1
(1.Beijing Institute of Control Engineering，Beijing 100190，China;2.China Great Wall Industry Corporation，Beijing 100054，China)

In order to improve the flexible vibration resulting from solar array，the PMSM(permanent magnet synchronous motor)is chosen to be the drive sources.A method of friction parameter identification and friction compensation is brought forward based on the LuGre model.Both static and dynamic parameters of the model are identified via the particle swarm optimization(PSO)algorithm.A friction torque measuring platform is designed，combined with which the proposed identification method is used to the test identification.From the comparison of simulation and test，the accuracy of the identification method is verified.The method is used to compensate the friction of SADA system，and the test results show that the method can improve the system’s tracking performance and decease the influences of friction.

SADA;PMSM;friction parameter identification;PSO

V448.2

:A

:1674-1579(2016)02-0014-06

10.3969/j.issn.1674-1579.2016.02.003

程俊波(1983—)，男，博士研究生，研究方向为航天器执行与驱动机构技术;张 强(1978—)，男，研究员，研究方向为航天器执行与驱动机构技术;虎 刚(1965—)，男，研究员，研究方向航天器执行机构技术;于国庆(1974—)，男，研究员，研究方向为航天器执行与驱动机构技术;陆栋宁(1982—)，男，博士，主要研究方向为航天器姿态控制技术.

*国家自然科学基金资助项目(61573060).

2016-01-19