基于多应用场景独立微电网储能系统优化配置

潘 华，邓长虹，吴之奎，何 俊，郭 芳

(1.武汉大学电气工程学院，湖北武汉430072；2.广东省电力设计研究院，广东广州510000)

基于多应用场景独立微电网储能系统优化配置

潘 华1，邓长虹1，吴之奎1，何 俊1，郭 芳2

(1.武汉大学电气工程学院，湖北武汉430072；2.广东省电力设计研究院，广东广州510000)

含风、光、储的独立微电网，科学配置合理的储能容量，能满足负荷供电需求，保证系统安全稳定运行。针对三种具有代表性的应用场景，分别提出了储能系统配置评价指标；以储能系统全寿命周期费用最优为优化目标，计及系统运行要求及蓄电池设备的特性约束，建立了孤网运行的微电网蓄电池储能系统的优化配置模型，并采用改进的粒子群算法进行求解；在容量配置的基础上，探讨了储能系统拓扑结构优化的方法。编写了优化设计软件并进行算例验证。

独立微电网；蓄电池储能系统；容量优化配置；改进粒子群算法；多应用场景

可再生能源被大量应用到微电网中，成为解决传统发电系统所带来的经济及环境等问题的重要方法。我国在风、光资源丰富的地区以及远离大陆的海岛建立了许多微电网系统，但是可再生能源具有的随机性、波动性，对系统的安全可靠运行造成了影响，特别是独立微电网，更加需要储能系统进行调节[1]。蓄电池作为发展最成熟的储能设备而被广泛应用于储能系统的建设。

本文针对现有研究的不足之处，提出了一种应用于孤岛模式下的微电网蓄电池储能系统 (BESS)容量优化配置的模型，对不同的应用场景提出不同的优化评价指标，采用改进的粒子群算法，从储能系统综合经济性最优的角度出发，以保证系统的安全可靠运行为前提，计及不同类型储能蓄电池设备的诸多约束条件进行容量配置求解。

1 含蓄电池的微电网系统建模

1.1 独立运行微电网的结构

独立运行的微电网主要由微电源(风电、光伏)、储能系统和负荷构成，典型的系统结构如图1所示。

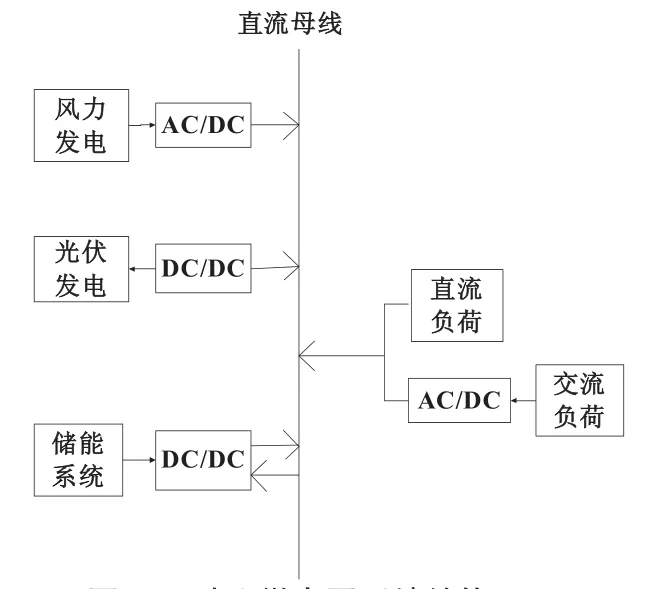
图1 独立微电网系统结构

1.2 BESS充放电建模

蓄电池储能系统的剩余电量在充放电过程中不断变化，其变化量与该时段内的充、放电电量和自放电有关。

蓄电池充电时：

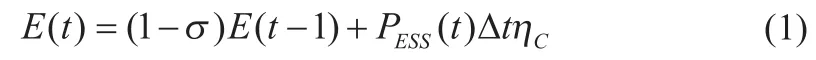
蓄电池放电时：

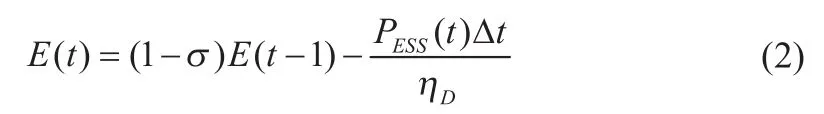
1.3 各种类型蓄电池特性

针对目前比较常用的、技术发展比较成熟的几种蓄电池，对其性能特点总结如下：

(1)铅酸电池是传统电化学电池的代表，是目前备用电源领域应用规模最大的电池类型，其技术和产业发展已非常成熟。铅酸蓄电池优点在于无记忆效应，成本相对较低；缺电在于循环寿命短，比能量小，质量和体积较大，自放电大且存在一定的污染。

(2)氢镍电池优点：具有较高的容量、结构坚固、充放循环次数多的特点；是密封免维护电池，正常使用过程中也不会产生任何有害物质；具有较好的低温放电特性，自放电率很小，可深度放电。缺点是有记忆效应，能量密度低，充电速度较慢，原材料制造成本较高。

(3)锂离子电池是新型绿色环保蓄电池，不仅具备高比能量、高比功率、高能量转换效率等优点，而且兼具长循环寿命；其缺点在于制造成本较高。

1.4 蓄电池串并联拓扑结构设计

蓄电池成组的串并联拓扑结构设计具有十分重要的意义，既要使实际使用的蓄电池单体数尽量接近理论计算值，又要为最大限度保持各电池单体充放电电流均匀而遵循“多串少并”原则。本文提出了一种蓄电池成组拓扑结构设计方法，包括以下步骤：

(2)根据工程实际情况计划采用的蓄电池用PCS型号；

2 基于多场景应用的BESS容量优化模型

2.1 目标函数

本文以BESS综合经济性最优为目标，以全生命周期费用对经济性进行衡量。根据IEC60300-3-3的规定，储能设备的全生命周期成本模型可定义为四大成本之和，即购置成本、运行成本、维护成本以及处置成本。在传统的优化目标中，通常只考虑储能设备的初始购置费用，忽略了在整个工程运行周期中蓄电池的运行、维护以及置换处理费用。如目前储能用的锂离子电池，虽然初始购置费用很高，但由于其充放电循环次数多，储能设备的折旧率很低，在较长时间的工程中，与需要相对频繁维护、更换的传统铅酸蓄电池相比，反而会显示出更优的经济性。

目标函数的具体表达式为[2]：

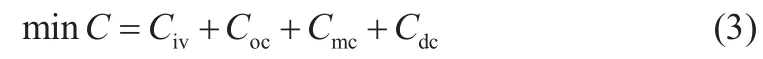
为避免优化模型过于复杂，本文引入折算系数来表示相应的成本，将式(3)改写为：

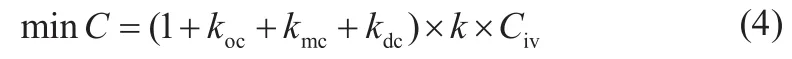
实际上，公共服务均等化供给受到的影响因素显然不限于本文所列举的几个变量。从回归结果中的拟合优度R2值比较低可以看出，我们无法在建模过程中把所有解释变量全部列出，因此三个模型不能排除因为遗漏变量而产生的内生性。

蓄电池的折旧率与其容量的损失直接相关，即当蓄电池进行深充深放时充放的电量低于一定值(本文取低于额定值的80%)时就需进行置换。定义蓄电池的初始额定容量为，运行一段时间后蓄电池的容量为，则此时蓄电池的折旧率为：

2.2 约束条件

在进行BESS容量优化时，一方面要考虑蓄电池设备本身的特性约束，另一方面要根据具体的应用场景考虑系统的运行约束。蓄电池的特性约束如式(6)所示：

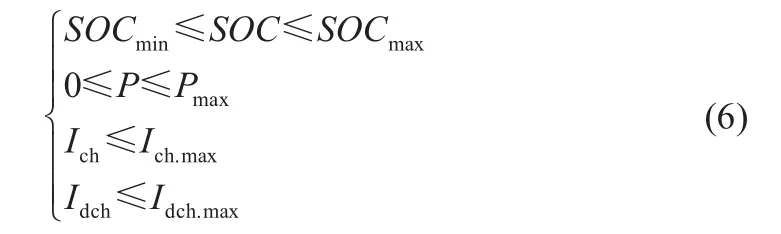
系统运行的约束条件和具体的应用场景有关。

(1)BESS作微电网后备电源

作为后备电源，储能系统应能配合风、光等新能源，满足负荷供电需求，使微电网的负荷缺电率 (loss of power supply probability，LPSP)小于制定值：

在此应用场景下以LPSP为衡量指标表征微电网系统的供电可靠性。

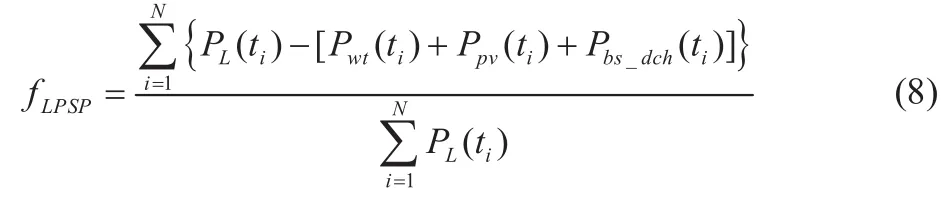
(2)BESS抑制风、光输出功率波动

由于风、光自然资源的随机性和间歇性，会导致风电、光伏发电的输出功率波动很大，随着可再生能源的渗透率不断增加，将给系统的安全稳定运行带来很大的挑战。本文提出以新能源的输出功率波动率(fluctuation of power supply probability，FPSP)来表征系统的输出功率波动情况。

然后根据系统运行的要求和新能源渗透率的不同制定输出功率波动率的目标值BD。通过储能系统的充放电调节，理想情况是使新能源的输出功率保持在区间[内。若通过蓄电池的调节，风电、光伏的输出功率仍超过了设定的功率波动范围，即：

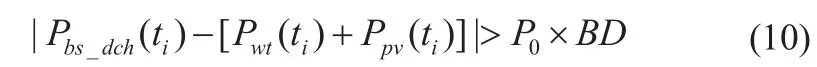
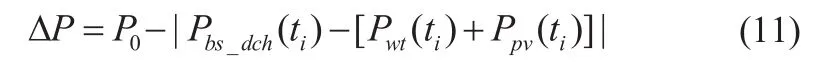
由式(12)得到FPSP的定义式：

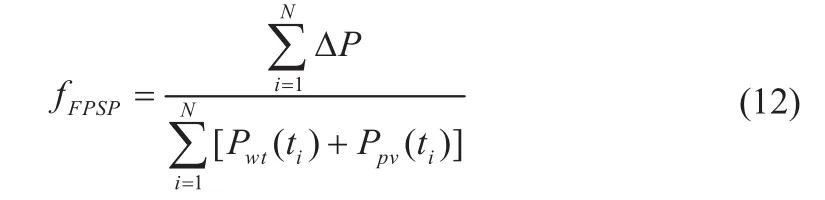
故此场景下的新能源输出功率波动率约束即衡量指标FPSP小于制定值。

(3)储能系统作重要负荷的全后备

微电网孤网运行时，没有大电网的支撑仅靠新能源发电，在资源条件不好时会导致负荷供电中断。针对微电网中的重要负荷，如机房、医院等，需要配置一定容量的储能系统在极端条件下持续供电一段时间。

此应用场景下，重要负荷在要求的保电时间内，应做到负荷缺电率为零：

2.3 改进的粒子群算法

本文采用改进的粒子群算法对优化模型进行求解。基本的粒子群算法思路见文献[3]：将每个优化问题的解看作是搜索空间内的一个粒子，所有的粒子具有一个由优化目标函数确定的适应度，还具有一个决定飞翔方向和距离的二维速度量。在迭代过程中，粒子根据自身最优解pbest和全局最优解gbest对自己的速度和位置进行更新。基本的粒子群算法收敛速度快，但容易陷入局部最优而导致收敛“早熟”。因此本文引入惯性权重，得到每个粒子的速度更新公式为：

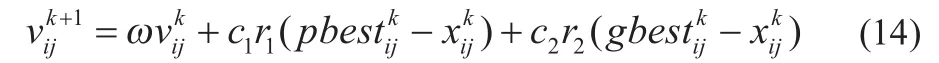
惯性权重对算法性能影响很大：较大的惯性权重有利于全局的探索，而较小的惯性权重有利于局部开发从而加快收敛。为解决这一问题，对ω采用如下的非线性动态惯性权重系数公式：

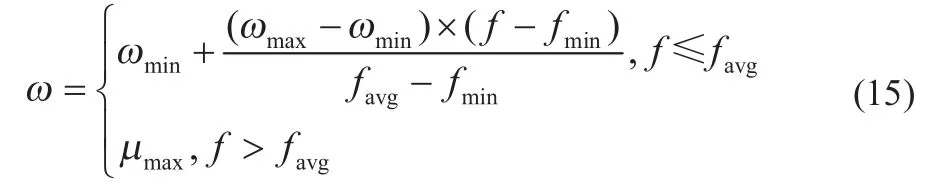
式中：ωmax、ωmin分别为ω的最大值和最小值；为粒子当前的目标函数值，和分别为当前所有微粒的平均目标值和最小目标值。

引入惯性权重系数ω，并采用自适应法确定其数值，可以针对算法初期目标函数的不同取值情况对权重进行不同处理，若趋于局部最优则加重权重，反之若各微粒目标值很分散则减小权重。对于取值不同的各微粒，将趋于最优解的微粒的权重减小，将取值相对较差的微粒权重因子加重，最终达到粒子群平均取值趋于最优的目的。除此之外，自适应权重法还能够根据目标值的变化而做相应的变化，从而使目标函数加速优化。

3 算例及分析

本文采用的算例为国内某一海岛的实际数据，为一典型的孤岛运行的微电网系统，其中包含10台260 kW的风力发电机，17组50 kW的光伏电池板。所选用PCS的端口电压上限值分别为150和50 V。该岛的月平均风速情况如表1所示。

该岛的月平均光照强度如表2所示。

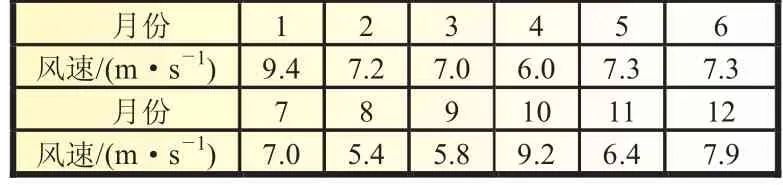
表1 算例风速数据

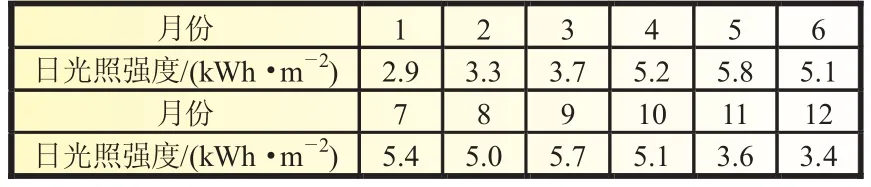
表2 算例光照数据

本文选用氢镍、锂电、铅酸等多种类型的储能蓄电池，针对具体的微电网算例，应用于不同的场景。其中，后备场景缺电率取值5%，抑制功率波动场景波动率取值10%，并在Matlab/Simulink下对优化配置出来的储能蓄电池容量进行了仿真验证。为了表现不同类型蓄电池的特性，所选用蓄电池的额定容量均为1 000 Ah、额定电压均为2 V，SOC初始值为80%，蓄电池的具体参数见表3。

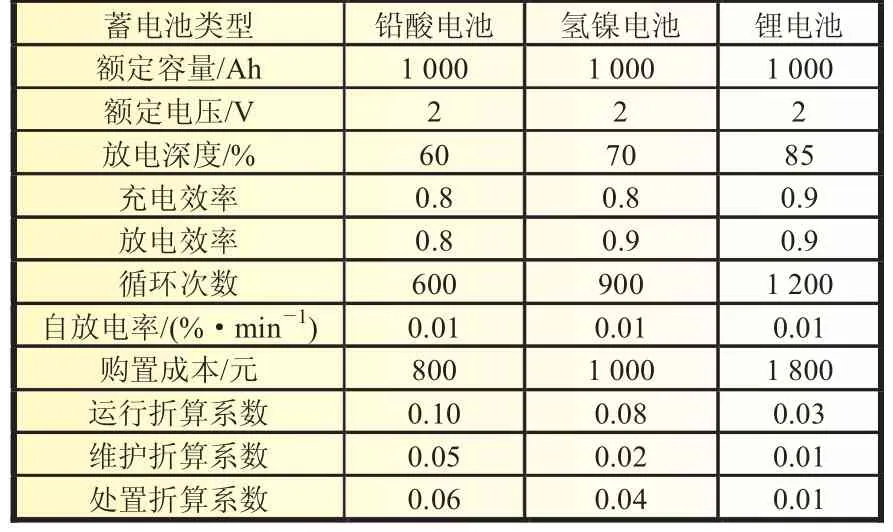
表3 蓄电池储能系统参数

3.1 储能系统作后备场景

缺电率取5%时储能容量配置结果如表4所示。该场景下的仿真结果如图2所示。

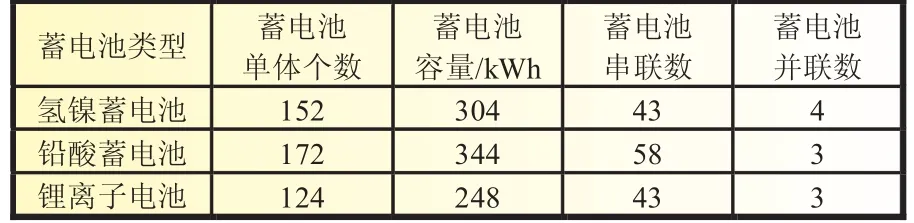
表4 储能作后备场景配置结果

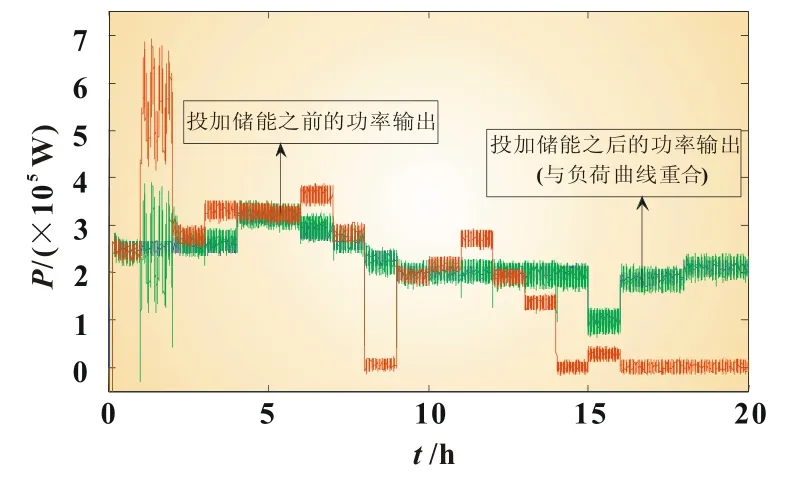
图2 蓄电池作后备场景仿真结果

3.2 储能系统抑制功率波动场景

取不同目标波动率时储能容量配置结果如表5所示。

该场景下的仿真结果如图3所示。

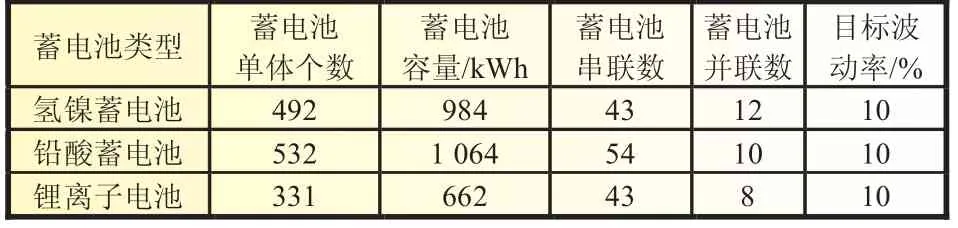
表5 储能抑制功率波动场景配置结果

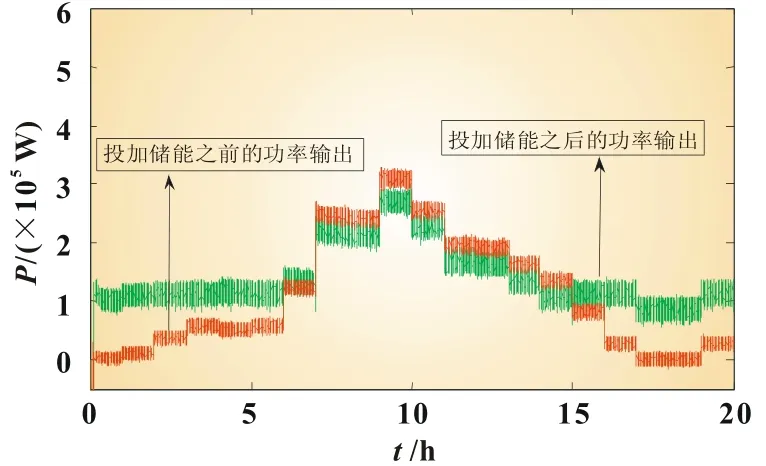
图3 蓄电池抑制功率波动场景仿真结果

3.3 储能系统作重要负荷的全后备场景

针对不同的保电负荷、保电时间的要求，配置出相应容量的蓄电池储能系统，结果如表6所示。

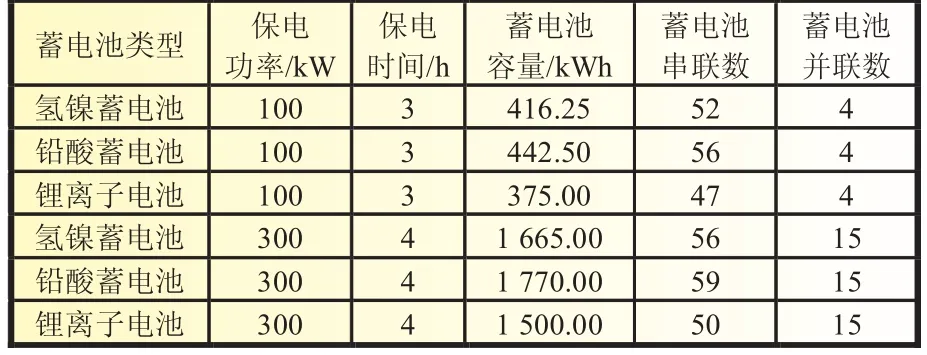
表6 储能作重要负荷的全后备场景配置结果

3.4 BESS全生命周期经济性效益

以不同类型的BESS的年平均费用来评价全寿命周期的经济性，其中年平均费用包括购置、运行、维护和处置等成本，以BESS作微电网后备电源为例，工程时间取10年，结果如图4所示。

如图4所示，锂电池储能系统相对其他两种类型的BESS，初始购置成本较高，但由于锂电池循环寿命较长，在长时间的工程运行中，反而显示出经济性优势，而铅酸蓄电池和氢镍蓄电池由于需要进行更换，使得年平均费用在4年以后高于锂电池储能系统的年平均费用。

4 结论

针对孤岛运行的风、光、储微电网系统，本文提出一种优化配置储能系统容量的方法。该方法以满足系统的安全稳定运行为前提，以实现全生命周期内综合经济性最优为目的，计及储能蓄电池的诸多约束条件，运用改进的粒子群算法对优化配置模型进行求解，同时对串并联拓扑结构进行设计。

在不同的应用场景下，根据不同的系统运行实际要求，配置出不同的储能容量，并进行仿真验证，由粒子群算法得到满足要求的最小容量。仿真结果表明，优化配置后的储能系统，在作后备场景下能满足负荷功率需求，在抑制功率波动场景下能明显减小波动范围，在作重要负荷全后备场景下能够在要求的时间内保证重要负荷的正常供电。算例的结果验证了该方法的合理性和有效性。

采用全生命周期作为经济性表征指标，比只考虑初始购置成本的经济性考核方法更符合实际情况，具有现实意义。

[1]丁明，王波，赵波，等.独立风光柴储微网系统容量优化配置[J].电网技术，2013，37(3)：576-581.

[2]崔新奇，尹来宾，范春菊，等.变电站改造中变压器全生命周期费用(LCC)模型的研究[J].电力系统保护与控制，2010，38(7)：69-73.

[3]李爱国，覃征，鲍复民，等.粒子群优化算法[J].计算机工程与应用，2002，38(21)：1-3.

Optimal design of energy storage system for independent microgrid based on multi-application situation

For an independent microgrid containing wind power,photovoltaic power and energy storage system,it is of great importance to configure reasonably the capacity of energy storage system to meet the electric power need of load and to make the microgrid system function safely and stably.Aiming at three typical scenarios,different indexes were presented.An optimal sizing method based on the modified particle swarm optimization was proposed.The method solves the optimal design problem on the premise that microgrids function safely.Various restrictions of batteries were taken into account, and finally the best sets of batteries were selected to achieve the optimal economic.In addition,the optimal design of topological structure of energy storage system was discussed.And optimization software was programmed and verified by calculation examples.

independent microgrid;battery energy storage system;capacity optimization;modified particle swarm algorithm;multi-application situation

TM 912

A

1002-087 X(2016)06-1269-04

2015-12-09

国家科技支撑计划(2013BAA02B02)；中央高校基本科研业务费专项资金(207274006)

潘华(1990—)，男，湖北省人，硕士研究生，主要研究方向为新能源发电中储能容量优化配置。