一种锂离子电池容量退化经验模型

2016-04-05韩裕生王瑾珏

电源技术 2016年6期

关键词：电池容量锂离子寿命

张金，魏影，韩裕生，王瑾珏

(1.解放军陆军军官学院军用仪器教研室，安徽合肥230031；2.偏振光探测技术安徽省重点实验室，安徽合肥230031)

一种锂离子电池容量退化经验模型

张金1，魏影1，韩裕生2，王瑾珏1

(1.解放军陆军军官学院军用仪器教研室，安徽合肥230031；2.偏振光探测技术安徽省重点实验室，安徽合肥230031)

锂离子电池随着时间的推移，其性能逐步下降退化直至寿命终结，往往会导致系统整体功能失效，应用于军事目的将直接导致各种无人作战系统无法完成战略战术预期，失去作战能力。分析了锂离子电池电学特性，给出电池内部阻抗与容量退化的关系，提出一种根据容量退化速率优先确定整数变量的条件三参数容量退化经验模型，并通过不同退化速率的锂离子电池退化实验数据对模型的可性行及实用性加以验证，为基于数据驱动的锂离子电池寿命预测和健康管理提供理论支撑。

锂离子电池；容量退化模型；三参数

锂离子电池由于其能量密度大、输出功率高、循环寿命长、工作温度范围宽、自放电小、绿色环保等优点，在军事通信、无人系统、便携式电子产品、航空航天等领域成为系统首选能源[1-2]。随着时间的推移，电池性能的下降以及意外的电池寿命终结，往往会导致系统整体功能失效，引起巨大的经济损失[2]，应用于军事目的将直接导致各种无人作战系统无法遂行战略战术预期，失去作战能力。2006年“火星探测者”号就是由于电池出现故障导致任务失败[1]。2011年爱默生网络能源有限公司的一项调查显示，导致数据中心停工事故的最大原因是不间断电源(UPS)的电池故障。2013年日本两架波音787客机由于机载锂离子电池过热引起燃烧，迫使全球波音787客机停飞。可见安全性是制约锂离子电池大规模应用的关键技术瓶颈[3]。电池寿命预测和健康管理 (prognostics and health management，PHM)使用户可根据底层条件做出维护决策，在失效之前给出预警，减缓危险系数。针对电池进行退化建模、寿命预测和健康管理，将大大提高电池供电系统的可靠性。

PHM有物理模型和数据驱动两种主要方式，数据驱动技术从电池性能数据如电流、电压、时间、阻抗等提取特征，使用统计学和机器学习跟踪电池退化从而估计其剩余寿命[3-4]。建立锂离子电池退化模型是预测其循环寿命的重要一环，但在实际工况中，根据锂离子电池内部的电化学过程来建立精确的电池退化过程模型很困难[5]。Bhaskar Saha等[6]首先开展了不同条件下的锂离子性能退化实验，获得了大量测试数据。在多个温度(40～70℃)下对锂动力电池进行加速寿命测试[7-8]，根据电池内阻与温度、荷电状态(SOC)与Δ%SOC的变化规律，提出了一个完全经验模型，并发展成多Sigmoid模型。Ramadass等[9]通过SOC、SEI膜电阻和扩散系数的变化来定量研究电池容量的衰减，提出电池容量退化的半经验模型。Gang等[10]在定量分析充电截止电压(end of charged voltage，EOCV)和放电深度(depth of discharged，DOD)对电池循环寿命影响的基础上完善了半经验模型。Wei He等[4]基于历史数据分析，提出一种由两个指数函数之和组成的模型来对锂离子电池容量退化过程建模。Bhaskar Saha等[11]利用来自于电化学模型的电池内部参数，建立一个指数增长模型来表达电解质电阻、电荷转移电阻和电池容量之间的关系，应用粒子滤波估计该模型的系数，采用关联向量机(relevance vector machines，RVMs)准确地跟踪电池退化趋势。然而，这种预测方法依赖于阻抗测量，由于电化学阻抗谱(electrochemical impedance spectroscopy，EIS)设备的高成本、严格的测量要求以及空间的限制等因素抑制了它在实际问题中的应用。

综上所述，电池的退化过程受温度、阻抗、EOCV以及DOD等多种因素的影响，模型涉及的参数越多，模型的准确性越高，然而在电池容量退化过程中，有些参数获取并不容易，涉及参数愈多，其建立就越复杂越困难。本文提出一种条件三参数容量退化模型，该模型在复杂性和准确性之间寻求最佳平衡，能够准确地拟合电池容量退化趋势的非线性。

1 锂离子电池退化过程分析

1.1 锂离子电池电学特性

锂离子电池一般由一对浸在电解液中的电极组成，化学驱动力来源于两个电极之间的化学势能差。由于循环充放电过程中，锂离子电池内部会发生一些不可逆的电化学反应，将导致电极上嵌入/脱出的Li+的损失，从而使其内阻增加，引起电池开路电压下降，影响电池的循环寿命。图1给出了几种因素影响下的电池典型极化曲线[12]，图中E0为室温25℃、1个大气压条件下测得的理论开路电压。

图1 电池典型极化曲线

电阻压降：形成电流环路时，由电解液内阻效应引起的电池本身的电压降。

活性极化：由内部电化学反应固有的动力学特性引起的各种迟滞因素，如Li+在电解液和电极接触面间运动所必须克服的逸出功。

浓差极化：离子在电极之间相互传递过程中质量扩散引起的电阻效应。

1.2 内部阻抗对容量退化的影响

除开路电压的下降，电池内部不可逆反应还将引起放电速率的下降，从而导致电池容量的退化。由图2[13]可见，电池容量随着电池的老化过程将会逐渐退化，即电池的容量随着电池充放电循环的增加而逐渐减小，达不到额定容量；同时电池的放电速率越大，电流越大，极化越严重，电池容量衰减得越快。

由此可见，电池内部不可逆化学反应引起其内部阻抗的变化是反映电池退化状态的重要参数。采用EIS法测得电池内部阻抗，经过分析大量的实验数据发现，电池容量与内部阻抗之间具有高度的线性相关性[14]，图3中RCT为电荷转移电阻，RE为电解质电阻，Warburg阻抗RW对电池退化过程的影响微不足道，一般忽略。

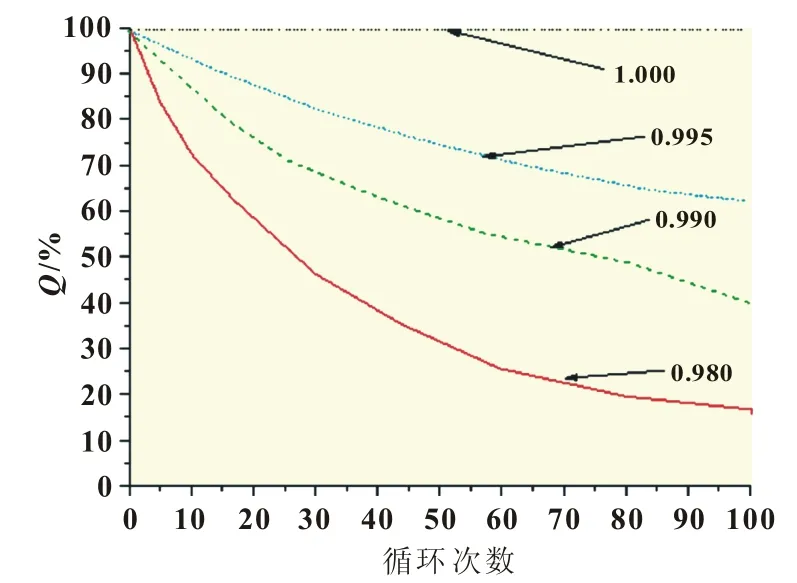
图2 典型的电池放电曲线

图3 容量和阻抗参数之间的相关性

2 锂离子电池容量退化模型

2.1 四参数容量退化模型及鲁棒性分析

由以上分析可知，电池的容量退化和内部阻抗增加是紧密相关的，而内部阻抗可用指数函数之和的形式表示[3]。基于此，不同退化速率的锂离子电池容量退化可表示为[4]：

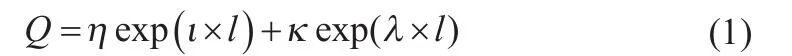
选用石墨阳极锂氧化钴阴极额定容量为0.9 Ah的商业锂离子电池，采用美国Arbin BT2000的锂电池实验系统在室温条件下进行循环充放电老化实验，放电电流为0.45 A，其中三组电池A1、A2、A3的容量退化数据如图4(a)、(b)、(c)中蓝色圆点所示。从容量退化趋势来看，尽管三组电池实验条件相同，但电池容量退化的速率却各不相同。根据式(1)得到的拟合曲线如图4(a)、(b)、(c)中红色粗实线所示。图4中容量退化数据来自于马里兰大学先进寿命周期工程中心。

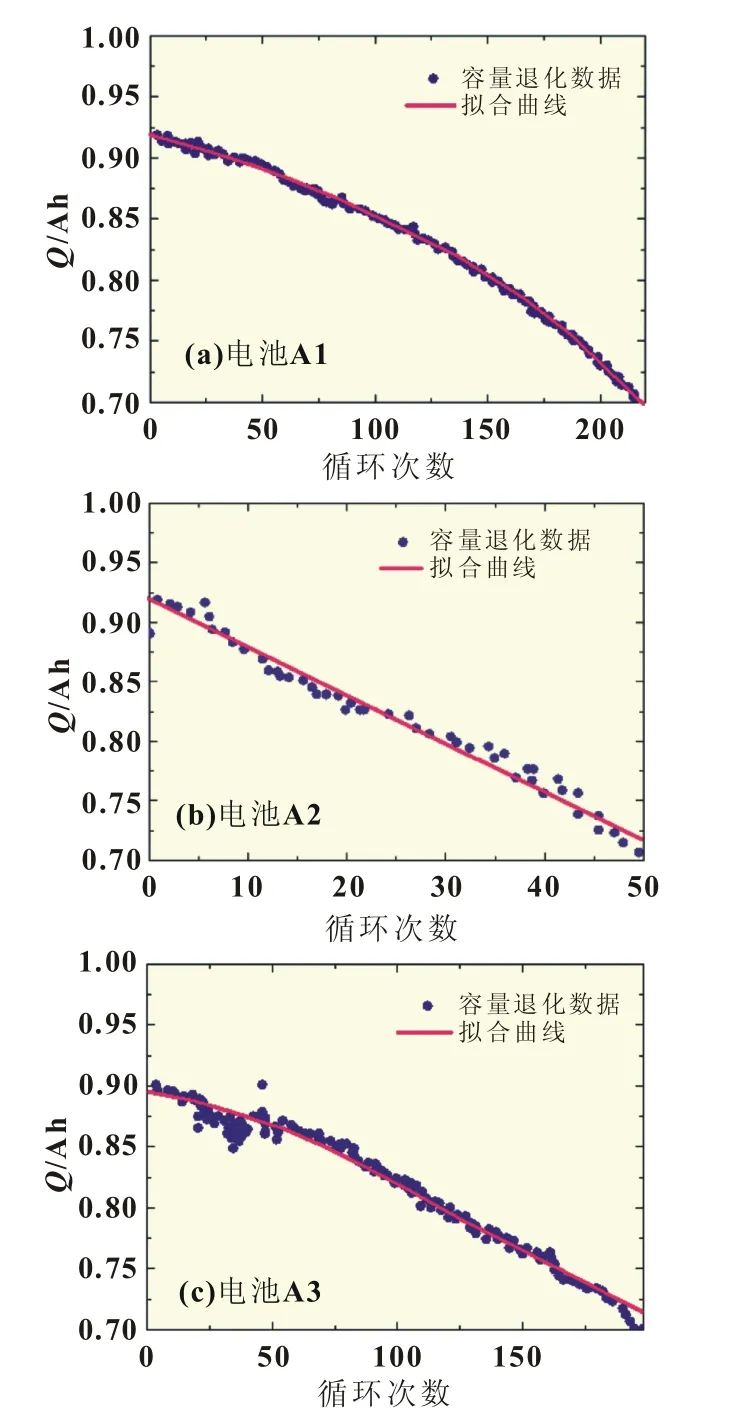
图4 电池A1、A2、A3容量退化数据及四参数模型拟合曲线

表1 容量退化四参数模型统计拟合度参数

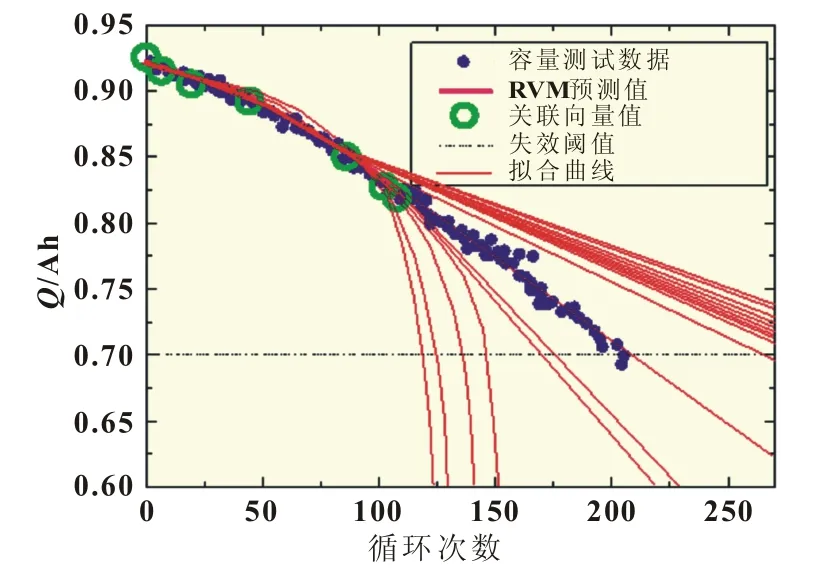
图5 由四参数容量退化模型得到的预测值拟合曲线不确定

2.2 条件三参数容量退化经验模型

由以上分析可见当仅仅有少量的容量退化数据时，公式(1)所示的四参数容量退化模型无法对预测平均值进行理想拟合。为获得唯一确定的数学模型，有必要在不丢失其函数功能的条件下对公式(1)做简化变形。由于指数函数能够展开成一系列幂函数之和的形式：

这样，式(1)中两个指数函数中的一个就可用一个幂函数来近似，于是得到：

对上述锂离子电池容量测试数据根据式(3)得到的拟合曲线如图6(a)、(b)、(c)细实线所示，均方根误差、决定系数以及调整相关如表2所示，这些数据说明式(3)能够对锂离子电池容量退化数据进行正确拟合。

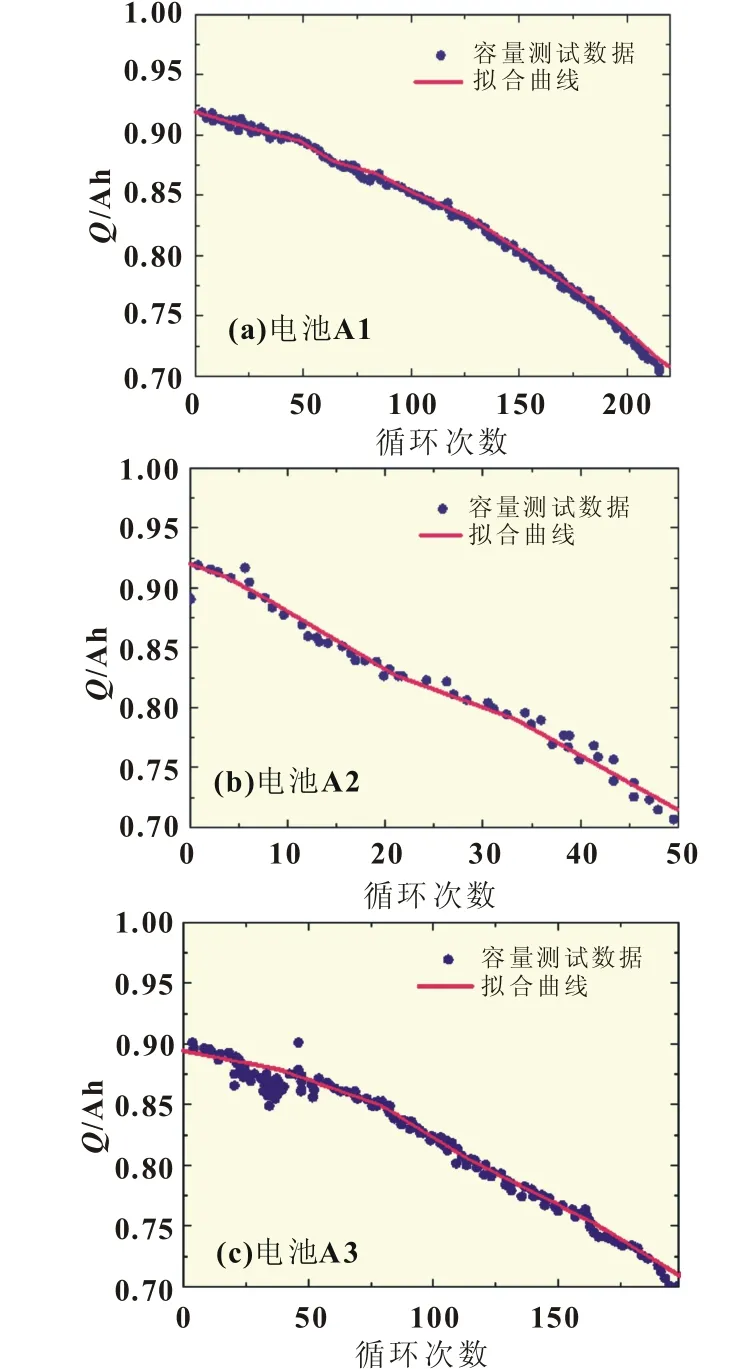
图6 电池A1、A2、A3容量退化条件三参数模型拟合曲线

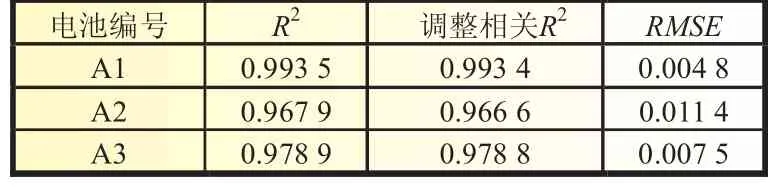
表2 容量退化四参数模型统计拟合度参数

表3 电池A1条件三参数退化经验模型参数估计值

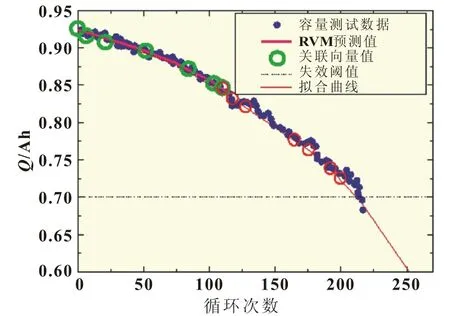
图7 由条件三参数容量退化经验模型得到的预测值拟合曲线唯一确定

比较图4和图7结果表明，本文提出的条件三参数容量退化经验模型拟合预测值具有唯一性，且参数维度少，计算简单。

3 结论

锂离子电池是一种新型绿色能源，安全性是制约其发展的关键因素，其性能随着时间的推移将逐步老化下降直至失效。由于锂离子电池的物理模型较复杂、失效机理难分析，运行过程一般是十分复杂且动态变化的，因此较难建立一个准确而通用的退化模型。本文根据锂离子电池电化学特性，得到其内阻变化与容量变化的对应关系。在此基础上对基于指数函数的锂离子电池四参数模型进行鲁棒性分析，依据数学原理对模型进行改进，提出根据容量退化速率优先确定整数变量的条件三参数容量退化经验模型。实验结果表明该模型参数维度少，计算简单，能对容量预测值进行唯一确定拟合，为锂离子电池剩余寿命预测及健康管理提供了一种理想的解决方案。

[1]王铭，李建军，吴扞，等.锂离子电池模型研究进展[J].电源技术，2011，35(7):862-865.

[2]ZHANG J L,JAYLEE.A review on prognostics and health monitoring of Li-ion battery[J].Journal of Power Sources,2011(3): 101-106.

[3]WANG D,MIAO Q,PECHT M.Prognostics of lithium-ion batteries based on relevance vectors and a conditional three-parameter capacity degradation model[J].Journal of Power Sources,2013, 239:253-264.

[4]HE W,WILLIARD N,OSTERMAN M,et al.Prognostics of lithium-ion batteries based on Dempster-Shafer theory and the Bayesian Monte Carlo method[J].Journal of Power Sources,2011,196: 10314-10321.

[5]罗悦.基于粒子滤波的锂离子电池剩余寿命预测方法研究[D].哈尔滨:哈尔滨工业大学,2012.

[6]SAHA B,GOEBEL K,POLL S,et al.Prognostics methods for battery health monitoring using a bayesian framework[J].IEEE Transactions on Instrumentation and Measurement,2009,58(2):291-297.

[7]WRIGHT R B,MOTLOCH C G,BELT J R,et al.Calendar and cycle-life studies of advanced technology development program generation 1 lithium-ion batteries[J].J Power Sources,2002,110:445-470.

[8]CHRISTOPHERSON J P,BLOOM I,EDWARD V T.Advanced technology development program for lithium-ion batteries:gen 2 performance evaluation final report[M].Washington:US Department of Energy,2006.

[9]RAMADASS P,HARAN B,WHITE R,et al.Mathematical modeling of the capacity fade of Li-ion cells[J].J Power Sources,2003, 123:230-240.

[10]NING G,RALPH E W,BRANKO N P.A generalized cycle life model of rechargeable Li-ion batteries[J].Electrochim Acta, 2006,51:2012-2022.

[11]SAHA B,POLL S,GOEBEL K.An integrated approach to battery health monitoring using bayesian regression and state estimation[C]//Proceedings of IEEE Autotestcon.Baltimore,MD:IEEE, 2007:646-653.

[12]SAHA B,GOEBEL K,CHRISTOPHERSEN J.Comparison of prognostic algorithms for estimating remaining useful life of batteries[J].Transactions of the Institute of Measurement and Control,2009,31(3/4):293-308.

[13]HUGGINS R.Advanced batteries:materials science aspects[M].New York:Springer,2008.

[14]GOEBEL K,SAHA B,SAXENA A,et al.Prognostics in battery health management[J].IEEE Instrumentation and Measurement Magazine,2008,11:33-40.

Empirical capacity degradation model of lithium-ion battery

With the time growing of lithium-ion battery,the performance of the batteries goes down or even gets over, and it always causes great loss both functionally and economically.In military applications,the failure will make unmanned combat system fail to carry out the strategic and tactical tasks.The electrical properties of lithium-ion batteries were analyzed,and the relation between lithium-ion batteries inner impedance and capacity degradation was set up.A conditional three-parameter capacity degradation model in which integer variable was determined firstly according to batteries capacity degradation rate was proposed.Three instance studies were conducted to validate the developed model.The results show that extrapolation of the conditional three-parameter capacity degradation model to failure threshold can be used to estimate the remaining useful life of lithium-ion batteries.

lithium-ion battery;capacity degradation model;three-parameters

TM 912

1002-087 X(2016)06-1176-04