在图形变换的操作对比中激活学生的想象思维
2016-04-05韩荣华张文良
韩荣华 张文良
(湖北省襄阳市襄州区朱集镇第三小学)
在图形变换的操作对比中激活学生的想象思维
韩荣华 张文良
(湖北省襄阳市襄州区朱集镇第三小学)
在小学几何初步知识中,经常出现计算阴影部分面积的几何问题,这些问题中,有阴影部分是单一的,也有阴影部分分布为两部分或两部分以上的,通常情况下阴影部分大都是一些不规则的图形,要直接算出每一部分的面积确实难以做到。如果在原图形的基础上,利用对称法(即翻转法)、平移法、旋转法将其进行等积、定性变换,把分散且不规则的图形重新组合成新的而又有规则的图形,那么,原来看似难以计算的问题就会变得极为简单了。
“等积、定性变换”说来容易,但在做法上还是很有窍门的,做得好,学生会学得又好又深,做得一般,学生只能机械接受。下面举几例来谈谈图形变换操作上的小窍门。
例1.已知:△ABC是等腰直角三角形,求图中阴影部分的面积。

操作方法:
1.画一画,先将画有图1的透明纸交给学生,要求:以OA(1 4圆半径)为轴,画出右圆的对称图形,即得到图2。
2.折一折,在图2中,以OA为轴对折。
3.对比分析:图2可以看作是由图1中完成以OA为轴的左圆与原图1所组合的图形(即例1中的图),图1又可看作是由图2中OA左圆向右翻转后与右圆完全重合后所成的图形。
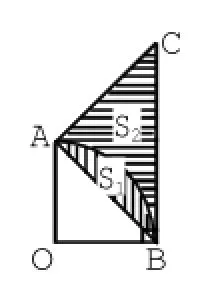
图1

图2
总结:一些不处于同一位置且不完全规则的图形,实质上是由同一位置上的且规则的图形用对称方法相对扩充后形成的,于是,在例1图中解决问题的思路就清楚了。


操作方法:
1.画一画,先交给学生两张透明纸,其中一张上画有图1,另一张空白,要求:将空白透明纸覆盖在图1上,并拓印出S2部分。
2.移一移,将拓印出的S2部分向右平移。
3.对比分析:图2可以看作是由图1中S2部分向右平移后形成的(即例2中的图),而图1又可看作是由图2中的S2部分向左平移后与S1部分对接组合而成的图形。

图1
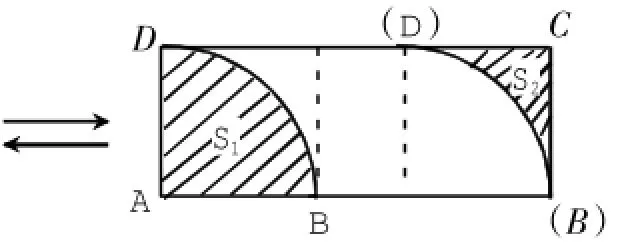
图2
总结:一些不处于同一位置且不完全规则的图形,实质上是由单一且规则的图形中的一部分经过平移分离后形成的,于是,在例2图中解决问题的思路就清楚了。
例3.已知:△ABC是等腰直角三角形,求图中阴影部分的面积。说明:例3中的两个图形实际上是同一个问题。
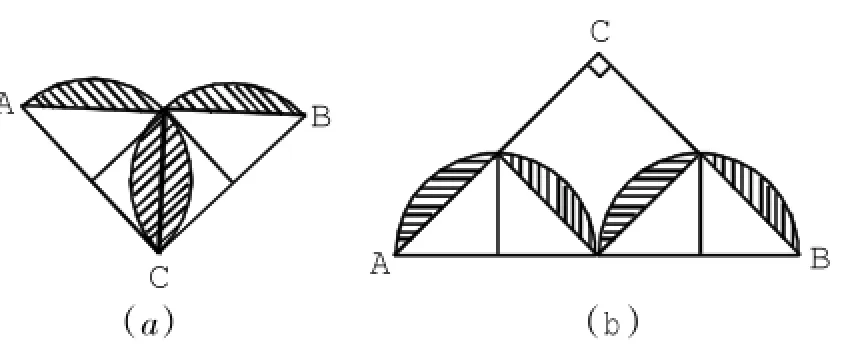
操作方法:
1.画一画,交给学生两张透明纸,其中一张上画有图1,另一张空白,要求:将空白透明纸覆盖在图1上并拓印出S3、S4或S1、S2所在的半圆。
2.转一转,以A为中心将S3、S4所在的半圆按逆时针旋转90°即得到上图2;以A为中心将S3、S4所在的半圆按顺时针旋转180°即得到下图2。
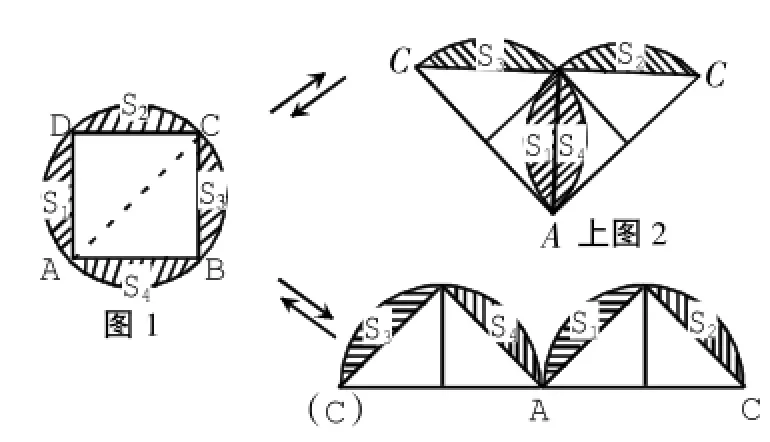
下图2
3.对比分析:上图2可以看作是由图1中S3、S4所在的半圆,以A为中心按逆时针旋转90°后形成的(即例3图(a)),而图1又可以看作是由图2中S3、S4所在半圆以A为中心按顺时针旋转90°后所得到的;下图2可以看作是由图1中S3、S4所在半圆,以A为中心按顺时针旋转180°后得到的(即例3图(b)),而图1又可看作是由图2中S3、S4所在半圆,以A为中心按逆时针旋转180°后得到的。
总结:一些不处于同一位置且不完全规则的图形,实质上是由同一位置上且又规则的图形经过旋转后形成的,于是,在例3图中解决问题的思路就清楚了。

综上所述,在通过图形变换对比中,学生的思维敏捷了,问题的思路清晰了,自然解决问题时也就胸有成竹了。
·编辑 鲁翠红
