多用户认知协作无线网络中的中继选择与载波分配策略★

徐加利，管章玉（1. 山东能源集团技术研发中心，济南50100；. 山东大学信息科学与工程学院，济南50100）



多用户认知协作无线网络中的中继选择与载波分配策略★

徐加利1，2，管章玉2
（1. 山东能源集团技术研发中心，济南250100；2. 山东大学信息科学与工程学院，济南250100）

摘要：在一个基于多载波的多主用户对-多次用户对-多认知中继节点组成的多用户认知协作无线网络中，本文考虑次用户网络采用underlay 频谱接入模式与主用户网络共享频谱，次用户中继节点采用译码转发的信号处理方式，在满足主用户对干扰温度限制的条件下，研究如何通过中继选择和载波分配以最大化次用户对的信道容量和。该问题首先被建模成为一个带复杂约束的非凸整数规划问题。通过问题等价转化，本文把两个二维0-1系数矩阵的联合优化问题转化为一个三维0-1系数矩阵的优化问题，继而原问题转化为0-1线性规划问题。因为变量之间互相耦合的特性，常规优化算法无法求解此问题，基于分支定界框架，本文设计了中继选择与载波分配最优算法。仿真结果表明，该算法的复杂度远低于穷举法（平均迭代次数少于2.5次）且总能取到全局最优性能。

关键词：无线通信；认知中继网络；中继选择；载波分配；分支定界；非线性整数规划

Citation: XU Jia-li, GUAN Zhang-yu. Relay selection and subcarrier allocation strategy in multiuser cognitive and cooperative wireless networks[J]. The Journal of New Industrialization，2016，6（1）:62-72.

0　引 言

认知无线电技术通过允许一组次要用户动态接入已经分配给主要用户的频谱，可以有效解决频谱使用效率低下的问题，通过引入协作中继技术，认知无线电系统的性能和频谱利用率可以得到更进一步提升，且可以带来系统的空间分集增益。因具有很好的对抗无线传输环境中的频率选择性衰落以及高频谱利用率的特点，OFDM技术非常适用于无线宽带信道下的高速传输。作为实现个人未来通信系统目标的有效方法（OFDM技术与协作中继技术已经被多个多个无线宽带系统标准如802.16e标准[1]和3GPP LTE-Advanced方案[2]作为关键技术采用），这几种技术的有效融合，将大力提升无线频谱资源的利用率，提高无线通信链路的可靠性和网络连通性。

对任何无线通信系统来说，资源分配问题始终都是研究的热点问题。不考虑认知无线电和协作通信技术的多用户OFDMA系统中的资源分配问题已经得到了较多的研究（如Cioffi等人的专著[3]），特别是基于不同优化目标对载波、比特和功率等的分配方案研究的热点，如[4，5，6，7]以及对应的参考文献。参考文献[8，9，10，11]研究了蜂窝网络中基于OFDM的多用户协作场景下的中继选择与载波分配问题。我们在前期工作[12，13]中研究了协作无线通信网络中的联合单中继选择与频谱分配问题。针对多信源-多信宿-多中继场景下的最优中继选择与子载波分配问题，[14]以中断概率最小化为目标，设计了基于随机二部图最大匹配（random bipartite graph based maximum matching，RBG matching）的算法。参考文献[15]考虑了基于OFDMA的认知无线电网络中的载波和功率分配问题，在次用户系统中考虑了一个次用户中继节点帮助次用户信源向多个次用户信宿节点广播数据，且主用户系统只考虑了一个信源-信宿收发对。[16]在基于OFDMA的认知协作无线网络中，基于对偶分解技术设计了子载波匹配、中继选择和功率分配的渐近最优算法，但是该文章只考虑了一个主用户信宿、一对次用户收发对的情况，而没有考虑多用户情况。[17]研究了认知协作Ad Hoc网络中路由、中继选择和频谱分配问题，采用跨层设计的方法提出了分布式算法，但是考虑的是overlay频谱接入方式，即只有某一子载波的授权用户不占用该频段的时候，次要用户才可以接入。

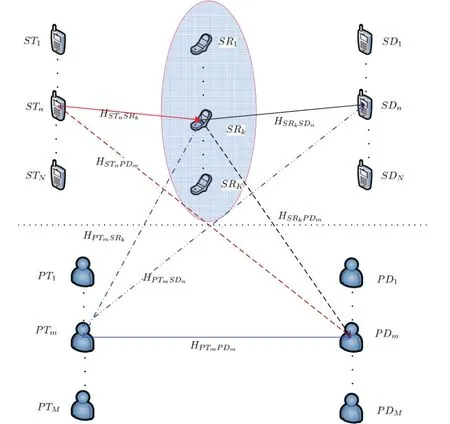
图1　多用户认知协作无线网络模型Fig.1 System model of multiuser cognitive and cooperative wireless network

1　多用户认知协作网络模型

本文所研究的多用户认知协作无线网络的系统模型如图1所示。 该系统有一个主要用户网络和一个次要用户网络组成。其中，主要用户网络有M个主要用户信源端（Primary Transmitter，PT）以及对应的主要用户信宿端（Primary Destination，PD）组建的M个主用户对组成，

假定多用户认知协作无线网络中的每个节点都只配备一根半双工全向天线。用分别表示从次用户发送端到次用户中继节点和主用户接收端在第w个信道上的信道增益；用和分别代表从次用户中继节点到次用户接收端和主用户接收端在第w个信道上的信道增益；用分别表示从主用户发送端到主用户接收端、次用户中继节点和次用户接收端在第w个信道上的信道增益。分别用分别表示第m个主用户发送端、第n个次用户发送端和第k个次用户中继节点在第w个子载波上的发送功率，其。

2　问题建模

在本文研究的工作中，我们对系统进行如下假设：

● 在每次通信过程中，每个主用户对最多只能占用一个载波，且每个载波只能被一个主用户对唯一占用。

● 在每次通信过程中，每个次用户对至多只能选中一个次用户中继节点，且每个次用户中继节点每次只能被一个次用户对唯一选中。

● 在主用户完成载波分配的基础之上，每个次用户组合只能占用一个载波进行通信。如果该载波已经被某一主用户对占用，则在一个通信周期的两个时隙内，在需要满足该主用户对的干扰温度限制条件下，次用户组合中的次用户发送端和次用户中继节点占用同一载波进行传输。

2.1中继选择模型

考虑到在每次通信过程中，每个次用户对至多只能选中一个次用户中继节点，且每个次用户中继节点每次只能被一个次用户对唯一选中。我们可以得到关于中继选择矩阵A的如下约束：

其中，约束条件（2）和（3）表示在该矩阵中，任何一行或者任何一列里面最多只能有一个1。

2.2载波分配模型

在我们的问题当中，主用户网络和次用户网络之间共享载波资源，当次要用户组合选用的载波已经被主用户对占用的时候，需要满足占用该载波的主用户对的干扰温度限制；当主用户没有占用该载波的时候，则不受干扰温度的限制。从实际的角度出发，在一个主次用户同时存在的网络里面，主用户享有对子载波分配的优先权。换言之，主用户网络的用户对可以根据某种原则首先进行子载波的分配。我们假定这一主用户载波分配的结果可以通过某种方式被次用户网络的用户知道。次用户网络的用户可以根据某种规则进行子载波分配，次用户可以独占空闲的子载波或者在满足主用户干扰门限的条件下与某一主用户对共享该子载波。

考虑在每次通信过程中，每个主用户对最多只能占用一个载波，且每个载波只能被一个主用户对唯一占用的限制，可以得到如下主用户子载波分配矩阵的相关约束：

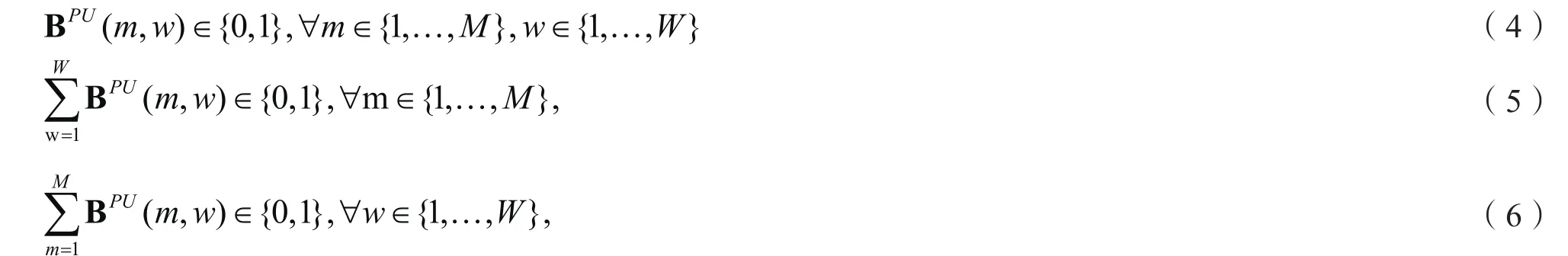
其中约束条件（5）和（6）分别表示在该矩阵中任何一行或者任何一列里面最多只能有一个1。 表示次用户发送端及选定的次用户中继节点选择占用子载波w，否则，表示不占用该子载波。可以得到如下次用户子载波分配矩阵的相关约束：

其中，约束条件（8）和（9）表示在该矩阵中，任何一行或者任何一列里面最多只能有一个1。

2.3多用户系统容量

当次用户网络中的中继节点采用译码转发（DF）的中继策略时，对次用户网络中的任意一个次用户收发对nn

STSD−来说，其链路容量表达式如下：SINRkSR代表第一个时隙中中继节点收到的信干噪比，代表第二个时隙中次用户接收端收到的信干噪比。下面，我们首先给出以上信干噪比的通用表达式。用代表被次用户发送节点nST和次用户中继节点kSR占用的子载波集合。那么我们可以得到的通用表达式如下：

以上公式中的分子部分表示接收端在占用的所有子载波上接收的有用信号功率之和；分母中的1为接收端收到的AWGN噪声的归一化功率，后面的两个表达式分别代表占用相同子载波的主用户和其他次用户造成的干扰。这些干扰的通用表达式如下：

在我们的问题中，当限定每个子载波只能分配给一个次用户组合使用时，其他次用户将不会产生干扰，即分别表示第一个时隙中所有工作在子载波w上的次用户发送端和第二个时隙中所有工作在子载波w上的次用户中继节点对主用户接收端mPD造成的干扰，其中：用一个M行W列的矩阵来表示M个主用户接收端在W个子载波上的干扰温度限制。用

2.4问题数学模型

本问题的求解目标是在满足主用户干扰温度限制的条件下，联合考虑中继选择和子载波分配策略以最大化次用户对的链路容量之和。公式表示如下：

3　中心式全局最优算法

在2.4节中描述的问题是一个0-1非线性整数规划问题，通常来说都是NP-hard问题。为了对问题进行求解，我们首先将对该问题进行等价变换使其转变为带约束条件的0-1线性整数规划问题，然后设计全局最优的中继选择与子载波分配算法。

3.1问题等价转换

为了进一步求解优化问题的最优解，我们定义如下几个新的变量：

●N*K*W的三维变量其中代表占用第w个子载波与通信时，接收到的信干噪比。

●N*K*W的三维变量其中占用第w个子载波与通信时，接收到的信干噪比。

●N*K*W的三维变量，其中代表占用第w个子载波选择作为中继节点与通信时，与之间的有效信干噪比。

●N*K*W的三维变量，其中代表占用第w个子载波选择作为中继节点与通信时，他们之间的信道容量。

经过以上的转化之后，我们的问题等价成为设计一个**NKW的三维0-1系数矩阵X，其约束条件如下：时，表示选择作为中继节点占用第w个子载波与建立通信链路。公式（27）-（29）表示的限制条件对应于在该三维系数矩阵中，任何一个二维平面上最多只能有一个1，其物理意义为任何一个次用户发送端最多只能选用一个次用户中继节点，同时最多只能占用一个子载波进行通信。此时原来的优化问题可以等效表示为：

其中，

公式（26）-（29）的限制条件

3.2算法设计

3.1节中（26）-（32）描述的问题是一个0-1线性整数规划问题，是一个NP-hard问题，采用穷举方法肯定可以得到此问题的最优解，但是当节点规模较大时，穷举法带来的复杂度将非常大。为了解决此问题，我们在本节基于分支定界算法框架，设计了可快速取到全局最优性能的算法。分支定界算法被认为是寻求非凸优化问题全局最优解的一种有效工具[18-21]，该算法框架的收敛性和全局最优性的理论证明可以参考[21]。针对本研究问题，分支定界算法框架的关键步骤包括：对原问题的优化函数或者限制条件进行放松，以得到一个便于求解的原问题上界；以放松后的解为出发点，通过设计本地搜索算法，得到一个原问题的可行下界；通过子问题选择和变量选择分割算法，将选定的子问题分割为两个子问题进行迭代求解。具体来说，就是首先将待求解变量从离散取值范围放松成为连续取值区间，求得原问题的一个放松解。本地搜索算法则是将待求解变量重新收敛到离散值。

下面，我们将对这几个步骤详细说明。

3.2.1放松问题及上界求解

本问题中的变量是三维系数矩阵中的每个0-1离散变量X(n,k,w)，为便于求解原问题的上界，首先将待求解变量从离散变量放松为连续区间变量，后面会再通过本地搜索算法再将变量收敛到0或者1，从而经过有限的迭代过程，最终得到最优性能解。将所有的优化变量X(n,k,w)从离散的{0,1}放松到连续区间之后，我们可以得到放松之后的优化问题如下：

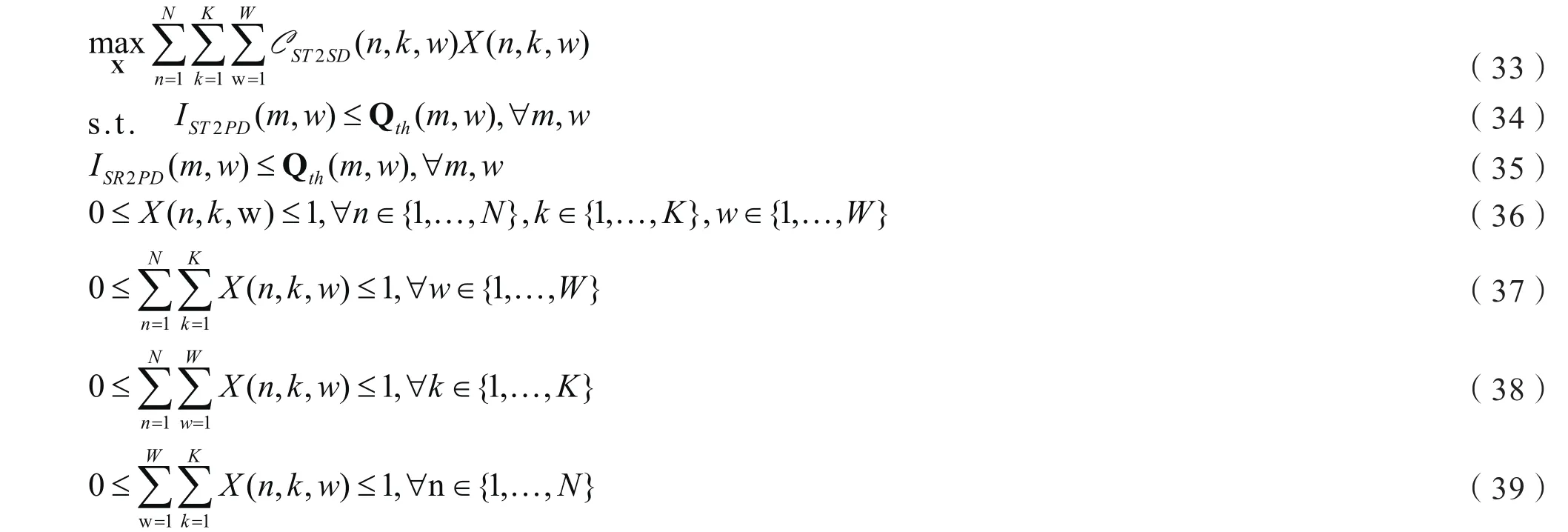
3.2.2本地搜索算法

上面经过放松之后的优化问题，可以使用内点法[22]等传统凸优化方法进行求解，得到一组最优解ˆX和对应的最优值ˆC。为了得到原优化问题的一组可行解以及对应的可行值，我们在本小节介绍的本地搜索算法中主要是在ˆX的基础上，将放松后的变量重新收敛到0或者1。

此处，采用对通过求解放松问题得到的解ˆX进行四舍五入取整运算，即：

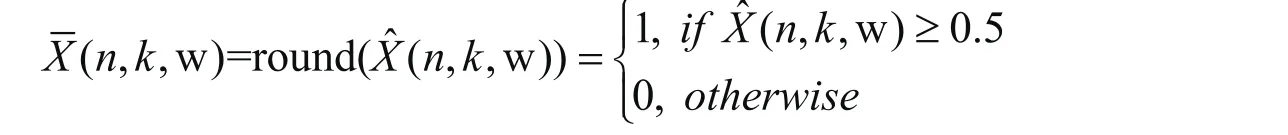
经过以上处理之后，在极个别情况下，会出现某一个二维平面上存在两个1的情况，这与本问题的限制条件不符。为了解决这个问题，我们采取如下措施：取整运算完成之后，当某一个平面上有两个1存在时，比较这两个1所在位置对应值的大小，保留值较大的变量值之后，代入目标函数可以求得原优化问题的一个函数值为1，将另一个置0。更新所有，作为原优化问题的可行下界。

本地搜索算法的详细描述如下：

本地搜索算法

for w=1:W

if 在某一平面上有两个1出现

3.2.3变量选择和分割策略

在基于分支定界算法的每个迭代过程中，若当前最大可行下界与最大上界仍无法满足迭代停止条件时，需要继续选定一个子问题，并选定该子问题中的一个未确定变量进行分割，从而生成两个新的子问题，进一步迭代求解。在我们的问题当中，我们选择具有最大上界的子问题进行分割。子问题选定之后，对分割变量的选择方法采用“不确定最大的值首先被分割”的原则。在我们的问题当中，由于需把待求解的变量确定为1或者0，因此，我们选定距离不确定性最大的0.5最近的变量首先进行分割，即

算法整体描述如下所示：

算法I: 全局最优中继选择与载波分配算法

输入变量:

主用户干扰温度矩阵Qth；

求解精度ε；

初始化:

迭代次数变量t=0；

迭代：

从子问题集合te中选择满足的子问题Q;

按照3.23节的方法，将子问题Q分割为QI和QII；

将子问题Q从et删除并加入QI和QII从而构成et+1；

输出：

LBt为满足原优化问题求解精度要求的最终函数值。

4　仿真结果与复杂度分析

4.1仿真结果

本节将通过仿真实验来验证3.2节中所设计算法的性能。仿真参数如下：

● 所有的信道都是单位方差、独立同分部（i.i.d.）的瑞利衰落信道；

● 所有主次用户的发送节点最多只能占用一个子载波且有相同的发送功率，即

● 求解精度=0.99ε；

● 所有仿真结果均是10000次Monte Carlo信道仿真后的平均值。

需要说明的是，在仿真中，主用户之间的载波分配算法不是我们研究的重点，此处我们采用以所有主用户对链路容量和最大化为目标的载波分配方法。

图2分别给出了主用户对数量M=5，次用户对数量N=5，次用户中继节点数量K=10情况下本文所设计中继选择与载波分配算法（图中用“proposed”表示）与通过穷举法（图中用“exhaustive”表示）取得所有次用户对链路容量和随子载波数量w变化的性能比较和本文所设计算法的平均迭代次数。从图中可以看出，本文所设计中继选择与载波分配算法可以取到全局最优性能且平均迭代次数在1到1.9之间。运行以上仿真过程所有的台式PC机配置如下：Windows XP 操作系统，Intel Pentium Dual E2200 @2.2 GHz CPU和2 GB的内存。运行以上仿真时，“exhaustive” （“proposed”）算法所用平均时间依次为:35秒（少于1秒），3分2秒（少于1秒），12分45秒34分44秒（少于1秒），1小时20分25秒（1秒），2小时43分50秒（少于3秒）。

为进一步验证所提算法性能，我们考虑在次用户中继节点数量K=8情况下，主次用户对以及整体系统的容量和随主用户对数量M和次用户对数量N、载波数量W变化时的三维性能曲线。需要说明的是，因为仿真过程中本文所设计算法始终可以取到全局性能，故没有再用proposed和exhaustive区分。图3分别从不同角度给出了主用户对容量和（图中用“PUs”表示）、次用户对容量和（图中用“SUs”表示）以及整个认知协作无线网络中所有主次用户对容量和（图中用“PUs+SUs”表示）。图4从不同角度展示了本文所设计算法的平均迭代次数，从图中可以看出我们的算法经过简单的几步迭代即可取到最优值。

4.2复杂度分析

为进一步比较本文所设计算法与穷举法的性能，我们将对这两种算法的计算复杂度进行定量分析。

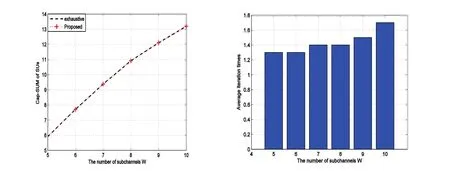
图2　所提方案与穷举法的系统容量和性能比较与平均迭代次数Fig.2 Aggregate system capacity achievable by the proposed scheme and exhaustive search and the number of required iterations

由3.2节中对本文所设计算法的描述可以得出，本算法的计算复杂度主要体现在对的三维变量中的每个元素的计算上，因此其算法复杂度为。而当采用穷举方法时，其计算复杂度为

综合以上仿真结果以及算法复杂度分析可知，在多用户认知协作无线网络场景中，本文所设计的中继选择与载波分配联合算法可取得全局最优性能且其运算复杂度远远低于穷举法。

图3　多用户认知协作无线网络中主次用户系统的SINR性能Fig.3 SINR performance of the multiuser cognitive and cooperative networks

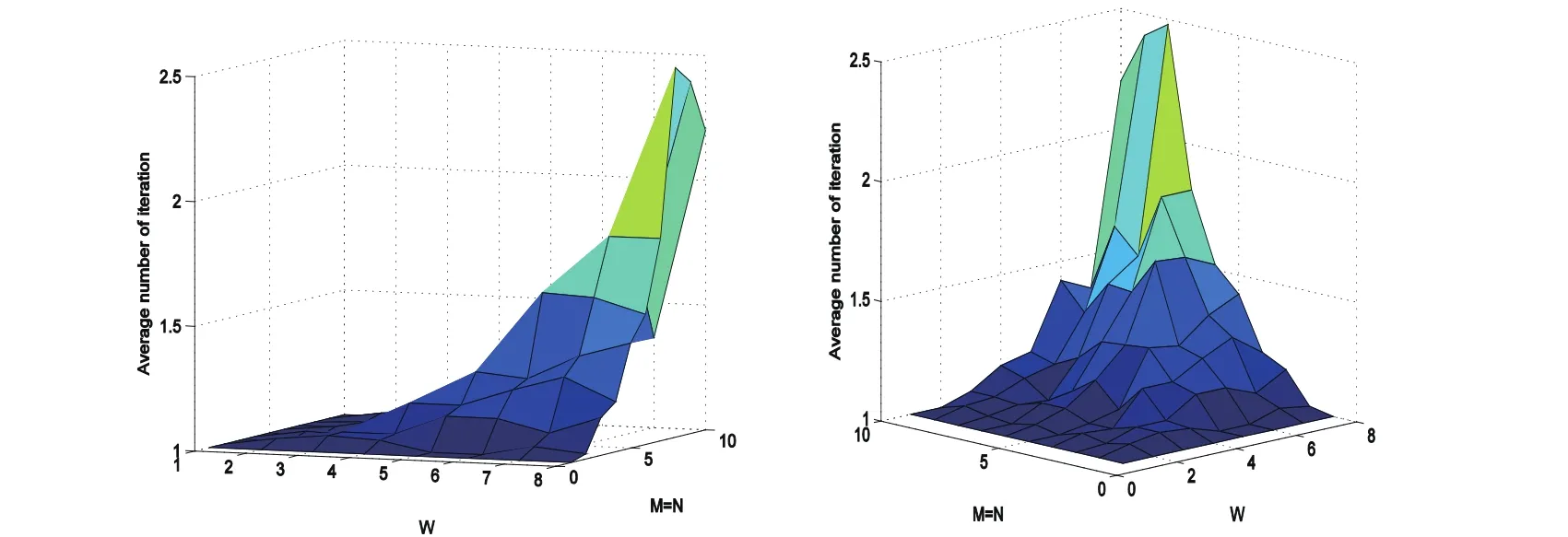
图4　不同角度下本文所设计算法平均迭代次数示意图Fig.4 Plot of average number of iterations required by the proposed algorithm （left），and its rotated version （right）

5　结论

本文研究了基于多载波的多用户认知协作无线网络中的中继选择与载波分配问题。我们考虑的多主用户对-多次用户对-多次用户中继节点组成的多用户认知协作无线网络中，次用户系统以underlay模式与主用户系统共享频谱，次用户中继节点采用两跳译码转发的信号处理方式，在满足所有主用户对干扰温度限制的条件下，通过中继选择和载波分配，最大化次用户系统的所有信道容量和。我们首先将联合优化问题建模成为一个具有复杂约束的非凸整数规划问题。通过等价转化，我们把两个二维0-1系数矩阵的联合配置问题转化为一个三维0-1系数矩阵的配置问题，基于分支定界算法框架，我们设计了可取得全局最优性能的中继选择与载波分配算法。数据分析与仿真结果表明，该算法的复杂度远低于穷举法（平均迭代次数少于2.5次）。

参考文献

[1] IEEE work group，IEEE 802.16e-2005. IEEE Standard for Local and Metropolitan Area Networks，Part 16 [S]. 2006.

[2] 3GPP. TR 22.951 Service aspects and requirements for network sharing [OL]. Tech. Rep.，December 2008. http://www.3gpp.org/ftp/Specs/ html-info/22951.htm

[3] J. M. Cioffi ，L. M. C. Hoo. Performance optimization in Orthogonal Frequency Division Multiplexing for Wireless Communications [M]. Springer，2006.

[4] C. Y. Wong，R. S. Cheng，K. B. Letaief，et al. OFDMA with adaptive subcarrier，bit，and power allocation [J]. IEEE J.Sel. Areas in Commun.，1999，17（10）:1747-1758.

[5] I. Kim，I. S. Park，Y. H. Lee.Use of linear programming for dynamic subcarrier and bit allocation in multiuser OFDM [J]. IEEE Trans. on Veh. Tech.，2004，55（9）:80-89.

[6] D. Kivanc，G. Li，H. Liu. Computationally efficient bandwidth allocation and power control for OFDMA [J]. IEEE Trans. Wireless Commun.，2003，2（6）:1150-1158 .

[7] 郝丽娜，宋金玲.自适应OFDM 及其改进算法[J].新型工业化，2011，1（7）：91-99.

Hao Lina，Song Jinling.Simulation of Adaptive OFDM and its improved algorithm[J].The Journal of New Industrialization，2011，1（7）：91-99. （in Chinese）

[8] Z. Han，T. Himsoon，W. P. Siriwongpaira，et al. Resource allocation for multiuser cooperative OFDM networks: Who helps whom and how to cooperate [J]. IEEE Trans. Veh. Technol.，2009，58（5）:2378-2391.

[9] W. Wang，S. Yang，L. Gao. Comparison of schemes for joint subcarrier matching and power allocation in OFDM decode-and-forward relay system [A]. Proc. IEEE Conf. Commun.，2008，4983-4987.

[10] Y. Li，W. Wang，J. Kong，et al. Subcarrier pairing for amplify-and-forward and decode-and-forward OFDM relay links [J]. IEEE Commun. Lett.，2009，13（4）:209-211.

[11] H. Shan，H. Wang，Z. Wang. Joint optimization of subchannel reassignment and power adaptation for multicarrier cooperative systems [A]. Proc. IEEE Conf. Wireless Commun.，Networking and Mobile Computing，2007，974-979.

[12] Z. Guan，T. Melodia，D. Yuan，D. Pados. Distributed Resource Management for Cognitive Ad Hoc Networks with Cooperative Relays [J]. IEEE/ACM Transactions on Networking，accepted for publication.

[13] 徐加利，管章玉．协作无线网络中基于遗传算法的联合中继选择与认知频谱接入机制[J]．新型工业化，2014，4（5）：41-47.

XU Jiali，GUAN Zhangyu.Joint relay selection and cognitive spectrum access based on Genetic Algorithm in cooperative wireless networks[J].The Journal of New Industrialization，2014，4（5）：41-47. （in Chinese）

[14] Bo Bai，Wei Chen，K.B. Letaief，et al. RBG Matching Based Optimal Relay Selection and Subchannel Allocation [A]. Proc. IEEE Conf. Commun. （ICC2011），2011，1-5.

[15] Jia Guo，Shen Gu，Xinbing Wang，et al. Subchannel and Power Allocation in OFDMA-Based Cognitive Radio Networks [A]. Proc. of ICC 2010，1-5.

[16] M. Shaat，F. Bader. Asymptotically Optimal Resource Allocation in OFDM-Based Cognitive Networks with Multiple Relays [J]. IEEE Transactions on Wireless Communications，2012，11（3）:892-897.

[17] Lei Ding，T. Melodia，S.N. Batalama，et al. Distributed Routing，Relay Selection，and Spectrum Allocation in Cognitive and Cooperative Ad Hoc Networks [A]. Proc. of Sensor Mesh and Ad Hoc Communications and Networks （SECON'2010），1-9.

[18] D. Li ，X. Sun. Nonlinear Integer Programming [M]. Springer，2006.

[19] Jens Clausen. Branch and Bound Algorithms - Principles and Examples[M]. 1999.

[20] 徐加利，张海霞，袁东风. 两跳放大转发中继网络中的ε-全局最优多中继选择策略[J]. 电信科学，2011，27（8）:39-44.

Xu Jiali，Zhang Haixia，Yuan Dongfeng. ε-Global Optimal Multiple Relay Selection Scheme for Dual-Hop Amplify-and-Forward Relay Networks [J]. Telecommunications Science，2011，27（8）:39-44. （in Chinese）

[21] S. Boyd，J. Mattingley. Branch and Bound Methods [OL]. http://www.stanford.edu/class/ee364b/notes/bb\_notes.pdf.

[22] Yu. E. Nesterov ，A. S. Nemirovskii. Interior Point Polynomial Algorithms in Convex Programming [M]. Philadelphia，SIAM，2004.

Relay selection and subcarrier allocation strategy in multiuser cognitive and cooperative wireless networks

XU Jia-li1, 2, GUAN Zhang-yu2
(1. R&D Center, Shandong Energy Group Co., Ltd., Jinan 250100, China; 2. School of Information Science and Engineering, Shandong University, Jinan 250100, China)

Abstract:The paper focuses on optimizing cooperative wireless networks where there are multiple primary users, multiple secondary users and multiple secondary relay nodes. The secondary users share a set of subcarriers with the primary users in underlay mode, and decode-and-forward strategy is used at the secondary relay nodes. The objective is to maximize the aggregate capacity of secondary networks by joint relay selection and subcarrier assignment, subject to the interference temperature constraints for the primary users. The resulting optimization problem is a constrained nonconvex integer programming problem, which is hard to solve because it needs to jointly optimize two bi-dimensional binary-coefficient matrices. To address this challenge, we propose to transform the original problem by transforming the joint matrices optimization into optimizing a single three-dimensional coefficient matrix, which can be further transformed to a binary linear programming problem. Since traditional optimization techniques cannot be directly applied because of the coupled variables, we design a solution algorithm based on branch and bound framework. Simulation results indicate that the algorithm can always achieve the global optimum with very low computational complexity （less than 2.5 iterations on average）.

Keywords:Wireless communications;Cognitive relay network; Relay selection; Subcarrier allocation; Branch-and-Bound; Nonlinear integral programming

通信作者：管章玉（1983-），男，讲师，山东大学信息科学与工程学院,主要研究方向：无线通信网络建模、分析与优化及其在多媒体通信网络、水下通信网络中的应用

作者简介：徐加利（1981-），男，高级工程师，山东能源集团技术研发中心,主要研究方向：智慧矿山、井下通信、认知中继无线网络

基金项目：国家自然科学基金（61101120），教育部博士点基金（20110131120028），山东省中青年科学家奖励基金（2012BSE27052）。

DOI：10.3969/j.issn.2095-6649.2016.01.004

本文引用格式：徐加利，管章玉.多用户认知协作无线网络中的中继选择与载波分配策略[J]. 新型工业化，2016，6（1）：62-72.