基于改进粒子群算法的无刷直流电机调速控制研究

黄 伟 王佳佳 谢 威 付家兴

（上海电力学院，上海 200090）

基于改进粒子群算法的无刷直流电机调速控制研究

黄 伟 王佳佳 谢 威 付家兴

（上海电力学院，上海 200090）

无刷直流电机（BLDCM）是一变量多、存在强耦合关系的复杂非线性系统，用传统的PID控制方法寻找合适的PID参数十分困难，进而很难提高BLDCM系统的控制性能。针对这一问题，基于粒子群算法优良的寻优能力，提出一种改进粒子群算法的BLDCM自适应PID速度控制算法。该算法对PID控制器的参数进行自整定，提高了PID控制器适应外在变化的能力。经过仿真发现，经优化后的BLDCM系统具有很好的静、动态特性，转速响应快，抗负载扰动能力强。

无刷直流电机 粒子群优化算法 自适应控制 PID

引言

当今社会，电机作为工业生产、家用电器等设备的重要执行部件，在很多场合要求必须具备精度高、速度快、效率高等特点。无刷直流电机也因为所具有的优异性能，得到了使用者的亲赖，主要表现在结构简单、效率高、没有励磁损耗、调速性能好等方面。尤其在当今大力提倡节能环保的大形势下，BLDCM高效率的特性更凸显了其应用的巨大潜力。因此，无刷直流电机的控制也成为研究的热点。

常规无刷直流电机一般采用传统的PID控制。传统PID控制是一种线性控制器，结构简单，需整定的参数少，是当今工业控制中应用非常广泛的控制算法。尽管传统PID控制器有这一系列优点，但它的缺陷也日益凸显。传统PID控制器要想取得满意的控制效果，必须找到合适的参数。在复杂的工业生产现场，负载、温度、压力等随时可能变化，甚至模型结构都会发生变化。其次，无刷直流电机所具有的非线性特点进一步增加了PID参数整定的难度。采用传统PID控制器，以整定好的PID参数去适应复杂变化的外界环境，想要达到满意的控制效果是很困难的。为弥补传统PID控制器存在这种不足，近年来，学者们提出了各种智能算法来优化PID控制器的参数，智能算法也在工控过程中逐渐被重视，并得到了一定程度的发展。

本文采用混合混沌粒子群算法优化PID控制器参数，通过利用Matlab中的Simulink工具箱搭建了电机控制系统的仿真模型。经仿真验证发现，该算法超调小，上升时间短，比传统PID控制具有更好的控制效果。

1 无刷直流电机的数学模型

无刷直流电机有多种工作方式，常见的两相导通星形三相六状态是应用最多的一种工作方式。在该工作方式下，电机出力大，转矩平稳性好且控制简单、性能优良。下面基于这种工作方式，分析无刷直流电机的数学模型。无刷直流电机具有一个很明显的特点，即BLDCM的反电动势、气隙磁场以及电流都不是以正弦波的形式存在。如果再采用交、直轴坐标变换的形式分析BLDCM，是不恰当的。直接采用无刷直流电机自身的相变量来构造数学模型，则更为简单明了。

为了便于分析，本文采用如下假设：

（1）电动机的气隙磁感应强度在空间呈梯形分布；（2）定子齿槽的影响忽略不计；

（3）电枢反应对气隙磁通的影响忽略不计；

（4）忽略电机中的磁滞损耗和涡流损耗；

（5）三相绕组完全对称。

1.1 电压方程

根据电机学原理，定子绕组的自感和互感参量只有在电机的转子磁阻不因转子位置的改变而发生变化时，参数自感和互感才是一个定值。此时，定子三相绕组的电压方程式为：

式中：ua、ub、uc为定子各相电压，R为定子电阻，ia、ib、ic为定子各相电流L、M为定子自感、互感，ea、eb、ec为各相反电动势。无刷直流电机的等效电路图如图1所示。

图1 BLDCM等效电路图

1.2 转矩方程和机械运动方程

BLDCM的机械运动方程为：

式中：Te为电磁转矩，w为电机转子角速度，B为阻尼系数，Tl为负载转矩。

2 无刷直流电机的控制系统结构

双闭环BLDCM调速系统的结构框图如图2所示。本文研究的主要目标是实现对速度的有效控制。为了减小外界干扰对系统的影响，取得理想的控制效果，电机调速系统采用速度电流双闭环控制结构：外速度环采用改进粒子群算法优化的PID控制器，内电流环采用常用的电流滞环控制器。此种结构能够一定程度地抑制外界扰动，更好的达到理想效果。

图2 无刷直流电机调速系统结构图

3 基于混合混沌粒子群算法的PID控制

3.1 粒子群算法

PSO算法是一种群体智能算法。该思想最初来源于对鸟类搜索食物的思考，后来经过一定程度的发展，应用在求解优化问题中。在粒子群对目标函数的寻优过程中，空间中的每个点都可看做是搜索空间中的一只鸟，称其为粒子。每个粒子都有一个由目标函数决定的适应度值和一个决定粒子飞行方向的速度值。粒子在搜索空间中以一定的速度飞行，通过粒子个体学习经验和群体学习经验之间信息的传递与共享，进而达到不断调节粒子飞行速度的目的。在每一次迭代计算中，粒子都会参考自己飞行过程中的最好位置Pbest和群体飞行过程中的最好位置Gbest来调节自己的位置和速度，使之不断向最优解附近靠拢。

粒子的位置和速度根据如下方程进行变化：

其中，c1和c2为学习因子或加速度系数，ε,η∈U[0,1]，是在[0,1]区间内均匀分布的随机数。

PSO通过追随个体极值和群体极值完成极值寻优，操作简单。在算法运行的初始阶段，收敛速度比较快，但随着迭代的不断进行，在粒子群不断收敛的同时，速度越来越慢，粒子越来越相似。多样性的缺失，使其无法摆脱局部极值点，这种现象被称为早熟收敛或停滞。针对这个问题，提出混合混沌粒子群算法。以下采用混合混沌粒子群算法对PSO进行改进。

3.2 改进的粒子群优化算法

3.2.1 混沌思想的引入

在非线性系统中，存有一种比较普遍的现象，这种现象被称为混沌。利用混沌运动具有的内在随机性、不重复、不紊乱等特点进行寻优搜索，可以防止陷入局部极值，进而提高优化速率，增强搜索的可靠性。因此，将混沌学嵌入粒子群的优化搜索中，与传统搜索方法相比，更具优势。

利用混沌优化算法的关键问题是如何实现混沌学与粒子群寻优算法的结合。本文采用载波的形式，将选用的混沌变量投射到待寻优参数的给定范围中，再用混沌变量实现参数寻优。采用Logistic映射来生成混沌变量，其迭代方程如下所示：

式中，μ是控制参数。当μ=4，0＜x0＜1时，Logistic映射处于完全混沌状态，并遍布整个[0,1]取值范围。

3.2.2 遗传算法中选择交叉机制的引入

标准粒子群算法在迭代寻优后期收敛速度慢，陷入局部极值的可能性很大。为此，引入遗传算法中的选择交叉机制，从群体中筛选出性能良好的粒子，则适应性强的个体就会被保存下来，而适应性差的个体将分别进行交叉操作。若交叉后的个体的适应值优于原来的粒子，则原来的粒子将被新粒子代替，反之保留原来的粒子。

3.3 混合混沌粒子群算法对PID参数的优化

传统PID控制器适应外在环境的能力比较差，控制器的参数整定后，就无法根据外在环境变化而进行动态调整，使得控制质量无法保持在最佳状态。利用混合混沌PSO算法优化PID控制器参数的基本思路，就是将控制器的Kp、Ki、Kd三个参数作为一个粒子，初始化粒子群的速度和位置，让其在给定范围内迭代寻优，最终得到参数最优值。

PSO优化算法步骤如下：

（1）确定控制器参数Kp、Ki、Kd的取值范围，同时设定群体规模Size、迭代次数MaxIter、加速常数c1、c2，利用Logistic映射产生N个混沌变量，即N个粒子的粒子群，并将N个混沌变量映射到优化变量的大致取值范围，完成微粒速度和位置的初始化。对于惯性权重，采用时变权重：

（2）评价每个微粒的适应度，适应度好的前N/2个粒子直接进入下一代，适应度差的N/2个粒子则进行交叉操作。本文选择的适应度函数为时间绝对偏差积分（ITAE)，它能够全面反应系统的控制效果和工业控制系统的特点。使用该适应度函数的主要目的，是改善系统的暂态响应，降低超调。

（3）对每个粒子，将其适应值与该粒子所经历过的最佳位置Pbest的适应值进行比较，将较好的那个值赋予此时的Pbest；同样，把粒子适应值和整个种群的历史最好位置Gbest的适应值进行对比。如过结果较好，则将其作为当前的Gbest。

（4）根据公式（4）、公式（5），改变微粒的速度和位置。

（5）若没有满足结束条件（通常为预设最大进化代数和适应值下限值），则返回（2）；反之，退出算法，得到最优解。

4 仿真实验

在Matlab/Simulink仿真环境下，搭建无刷直流电机控制的仿真模型，如图3所示。

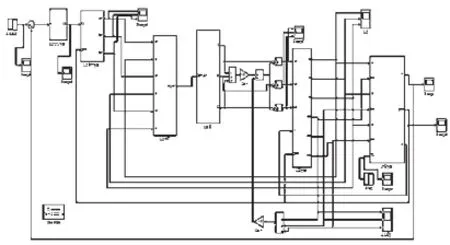
图3 BLDCM调速系统仿真模型

BLDCM电机参数设置为：极对数P＝1、定子相绕组电阻R＝2.0Ω、定子相绕组自感L＝0.025H、定子绕组互感M＝-0.0065H、额定转速n＝1000r/min、阻尼系数B＝0.002N·m，转动惯量J＝0.006kg·m2，饱和限幅模块幅值限定为±35，逆变器电源采用220V直流。

系统空载启动时额定转速n=1000r/min，在t=0.2s时加速到n=1200r/min，在t=0.3s时加负载TL=12Nm，在t=0.6s加负载TL=8Nm。运行无刷直流电机仿真模型，转速响应曲线如图4所示。

图4 转速响应曲线

由图4仿真波形可以看出，传统PID控制在电机启动时响应速度比较慢，在0.1s左右才达到了稳定状态；在0.2s突然加速后，经过0.08s达到稳定状态；在0.3s和0.6s突加负载后，转速波动比较大，转速突降达到20%。未改进的粒子群算法，在电机启动时存在较大的超调，超调为4%；在0.2s突然加速时，也能快速响应到额定转速；在0.3s以及0.6s突加不同大小的负载后，转速下降，较传统PID控制小。而在基于改进PSO算法优化的PID控制下，响应快速且平稳，超调量小，在突加负载之后，转速波动很小，范围在2%以内。整体而言，改进的粒子群自适应控制算法比传统的PID控制具有更好的控制效果。

5 结论

本文对无刷直流电动机采用基于混合混沌粒子群优化的PID控制算法，有效克服了传统PID控制器参数不能自寻优的缺点。仿真结果表明：用改进粒子群优化的无刷直流电机PID控制器的调速控制系统，比采用常规PID控制器的调速控制系统控制效果更佳，不仅超调量小，而且在系统参数和负载扰动变化时能够迅速恢复到稳定运行状态，具有较强的适应环境能力。

[1]张鑫，党建武，王阳萍.基于PSO的多叶准直器PID控制器参数优化研究[J].兰州交通大学学报，2013，32（6）：15-18.

[2]王永宾，许军，周奇勋.改进重置粒子群算法在MPC调速系统中的应用[J].微电机，2015，48（5）：79-84.

[3]钟福龙.基于粒子群优化的线性离散冶金控制系统[J].世界有色金属，2016，（3）.

[4]丁恒兵.改进协同量子粒子群算法在流水车间调度中的应用[J].数字技术与应用，2015，（1）：133-134.

[5]吴伟，张康康.基于智能算法的轮式机器人控制系统优化设计[J].AA电气工程学报，2015，10（12）.

[6]谢铮桂，钟少丹，韦玉科.改进的粒子群算法及收敛性分析[J].计算机工程与应用，2011，47（1）：46-49.

[7]王洪涛，任燕.一种动态多种群粒子群优化算法[J].微计算机信息，2011，（12）：144-146.

[8]戴莹.基于BP神经网络的无刷直流电机PID控制方法的研究[D].合肥：合肥工业大学，2007.

[9]王瑾，张求明，黄波.粒子群优化算法的分析与研究[J].中国地质大学计算机学院，2009，13（2）：32-35.

[10]Zhang L P，Yu H J，Hu S X.Optimal Choice of Parameters for Particle Swarm Optimization[J].浙江大学学报A：英文版，2005，6（6）：528-534.

[11]刘颖.微型飞行器动力装置特性研究[J].南京航空航天大学，2007，11（3）：25-30.

[12]付光杰，杨皋润，高俊莹.基于粒子群算法的无刷直流电机控制研究[J].组合机床与自动化加工技术，2013，（6）：95-98.

[13]陈昊，厉虹.基于粒子群算法的无刷直流电机调速系统应用研究[J].北京信息科技大学学报：自然科学版，2008，23（4）：53-57.

Brushless DC Motor Velocity Adjustment Research based on Improved Particle Swarm Optimization Algorithm

HUANG Wei, WANG Jiajia, XIE Wei, FU Jiaxing
(Shanghai University of Electric Power,Shanghai 200090)

Brushless DC motor(BLDCM) is a multivariable ,strong coupling,complex and nonlinear system，so it is difficult to find a suitable PID parameter and improve the controlling effect for BLDCM.In order to solve this problem, an adaptive PID controller algorithm based on improved particle swarm optimization is proposed. The ability of excellent optimizing was used to adjust parameters ,so as to improve the ability of PID controller to adapt to the environment.The simulation results proves that the system has a better static and dynamic performance, and the speed response is fast．At the same time ,the algorithm has a strong adaptability for changes of the load disturbance.

brushless DC motor, PSO, adaptive control, PID

上海市电站自动化技术重点实验室（13DZ2273800）。