横肋粗糙元地表的风场阻力特征研究
2016-04-05武建军
李 冰,江 岸,武建军
(兰州大学西部环境与灾害力学教育部重点实验室 土木工程与力学学院,甘肃兰州 730000)
横肋粗糙元地表的风场阻力特征研究
李 冰,江 岸,武建军*
(兰州大学西部环境与灾害力学教育部重点实验室 土木工程与力学学院,甘肃兰州 730000)
使用雷诺应力模型(RSM)模拟横肋粗糙元地表的风场,将粗糙元横截面的高宽比h/b、粗糙元间距宽度比w/b以及间距高度比w/h作为粗糙表面的特征参数,利用数值方法定量研究了粗糙表面阻力随粗糙元密度的变化规律以及粗糙元横截面尺寸改变对阻力的影响。研究结果表明:粗糙元横截面尺寸改变不影响粗糙表面阻力随粗糙元分布密度的变化规律,粗糙元的间距高度比w/h是横肋粗糙表面的关键特征参数,且粗糙表面的平均总阻力在w/h=7时取得最大值。
横肋粗糙元;摩擦阻力;形状阻力;平均总阻力
0 引 言
粗糙表面的流动在现实生活中十分常见,流体工程中也常常使用粗糙表面来增强对流换热效果,但这往往增大了表面阻力[1],横肋粗糙表面经常作为简化模型用来研究粗糙元对流场的湍流结构[2-5]、阻力[6-9]和传热[10]等的影响。Perry等[11]通过实验研究零压力和逆压力梯度条件下横肋粗糙表面湍流边界层的发展,认为粗糙表面的阻力由分布在粗糙元表面的压强决定。Furuya等[6]通过风洞实验研究了圆形截面金属线形成的粗糙表面的湍流运动,通过测量粗糙元表面的压强揭示出粗糙表面的阻力主要是形状阻力。Okamoto等[10]通过水槽和风洞实验研究横肋粗糙表面流场的流动形态和传热系数随粗糙元分布密度的变化规律,但没有对阻力进行深入研究。Leonardi等[7-8]通过直接数值模拟(DNS)的方法研究了方形截面粗糙元形成的横肋粗糙表面流线旋涡的形态以及阻力随粗糙元间距增加的变化规律,结果表明形状阻力在粗糙元间距高度比w/h=7时取得最大值,并认为w/h值是横肋粗糙表面的关键特征参数,但没有考虑粗糙元横截面尺寸的影响。Ashrafian等[12]在Leonardi等[7]研究基础上,使用直接数值模拟(DNS)的方法研究w/h=7时横肋粗糙表面的湍流特性,将瞬时速度云图中出现的延长条纹结构与Leonardi等[7]的结果进行对比,认为至少对粗糙元分布比较稀疏的情况,粗糙元高度和粗糙元间距同为影响横肋粗糙元表面流动的关键参数。
己有文献在研究中多用横截面为圆形和方形的横肋粗糙元,只对应横截面高宽比h/b=1的情况。本文使用雷诺应力模型(RSM),将粗糙元间距宽度比w/b、粗糙元高宽比h/b和粗糙元间距高度比w/h作为横肋粗糙表面的特征参数,通过改变粗糙元横截面的尺寸,研究粗糙表面阻力随粗糙元密度的变化规律以及粗糙元横截面尺寸对阻力的影响,并从阻力角度判断横肋粗糙表面的关键特征参数。
1 理论模型
1.1 基本控制方程
考虑湍流脉动的影响,通常使用雷诺平均法,将速度(ui)和压力(p)分为时均项和脉动项两部分,即其中和分别为速度和压力的时均项和分别为速度和压力的脉动项,将用时均项和脉动项表示的速度和压力代入瞬时连续性方程和纳维-斯托克斯方程,并对时间取平均,即可得到时均形式的连续性方程和纳维-斯托克斯方程。简便起见,省略时均项上的横线,则时均形式的连续性方程和纳维-斯托克斯方程表示如下:
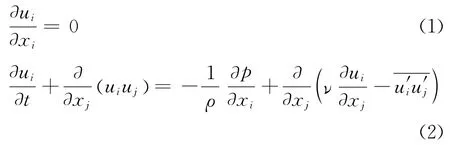
1.2 湍流方程的封闭
时均形式的纳维-斯托克斯方程比时均化之前多了一个新未知量常被称为雷诺应力项,要使湍流方程封闭则必须求解雷诺应力项。雷诺应力方程模型(RSM)摒弃了Boussinesq假定,考虑雷诺应力的对流和扩散效应[13-14],构造雷诺应力的输运方程,这种处理方式更加符合物理实际[15],适合模拟一般复杂的流动。
雷诺应力输运方程具有如下形式:
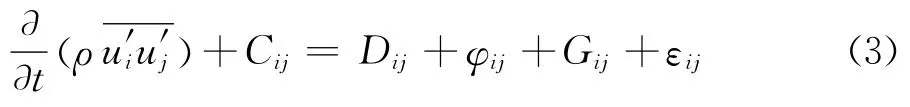
其中,Cij为雷诺应力的对流项;Dij为扩散项,影响湍流动量的空间分布;Gij为雷诺应力的产生项;φij为雷诺应力的再分配项,影响湍流动能在法向应力分量中的分布,本文使用的是再分配项的LRR模型;εij为雷诺应力的粘性耗散项。模型化后各项具体的表达式如下:
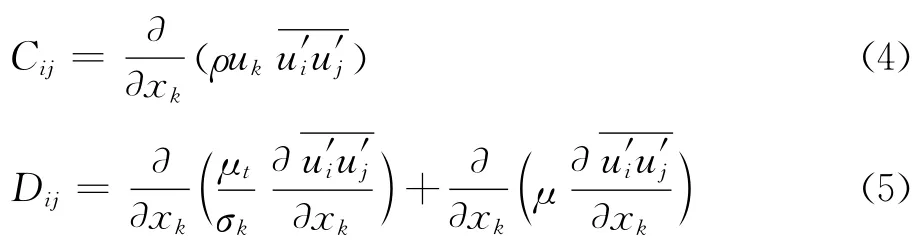
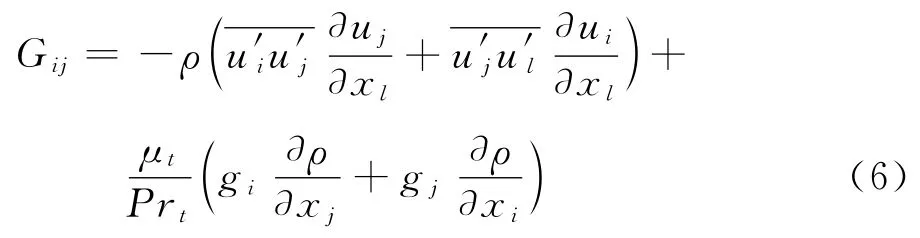
式中,gi和gj分别代表重力加速度在i方向和j方向的分量,Prt=0.85为普朗特常数。
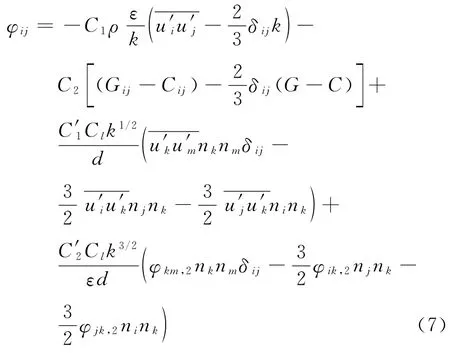
δij为kronecker delta,i=j时,δij=1;i≠j时,δij=0。C1=1.8,C2=0.6,G=1/2Gkk,C=1/2Ckk,Cij和Gij分别见式(4)和式(6),C′1=0.5,C′2=0.3,Cl=为卡门常数,nk为壁面单位法向量的xk分量,d为计算位置到壁面的垂直距离。

雷诺应力输运方程含有湍动能k和湍流耗散率ε,故还需补充湍流动能k和湍流耗散率ε的方程:
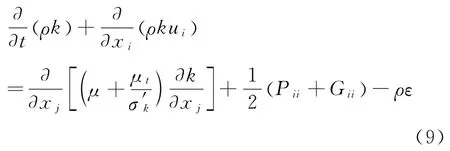
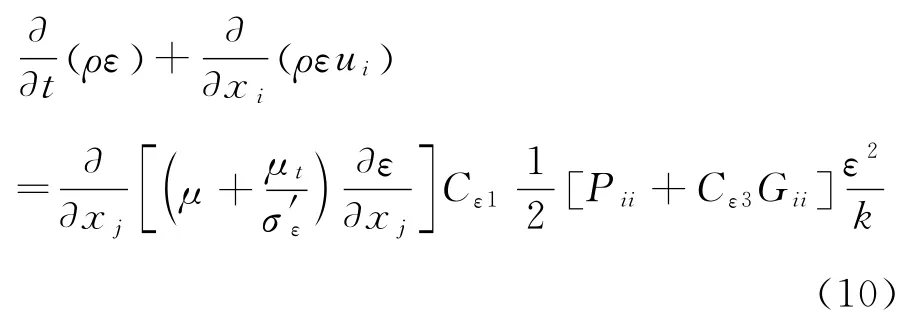
其中,σ′k=0.82,σ′ε=1,σε1=1.44,σε2=1.92,Cε1=1.44,Cε2=1.92,Cε3=tan|v/u|,v为与重力方向平行的流速分量,u为与重力方向垂直的流速分量。
2 数值计算模型
数值计算域为长方形,顶面光滑,底面铺有等间距排列的横截面为矩形的横肋粗糙元。图1给出了计算域的示意图。粗糙元横截面高度为h,宽度为b,相邻粗糙元之间的间距为w。λ=w+b,看作一个单位长度,计算域长度L=3λ,高度H=0.2m。Ub为入口的平均风速,风场方向从左至右,AB面为粗糙元的迎风面,CD面为粗糙元的背风面。对计算域的入口和出口设置周期性边界条件,能够使湍流发展的足够充分,同时有效地降低计算量,提高计算效率。
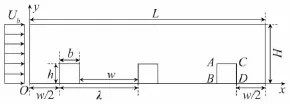
图1 计算域示意图Fig.1 Computational field diagram
图2给出了近壁面单元划分图。x方向和y方向均为非均匀网格,靠近壁面的部分尤其是粗糙元附近网格尺寸较小,网格分布比较密集。

图2 计算单元划分Fig.2 Computational grid
边界条件如下:
入口和出口为平移周期性边界条件:ui(xo,yo)=ui(xL,yL)
其中,(xo,yo)为入口边界任意位置坐标,(xL,yL)为与入口对应的出口位置坐标;
上表面和下表面为固定壁面:
ui=0。
Re=Ub·H/2ν,ν=1.46×10-5m2/s为空气的运动粘度。
3 计算结果及分析
3.1 数值模型验证
Okamoto等[10]通过风洞实验测量了不同粗糙元分布密度时,横肋粗糙表面粗糙元之间和粗糙元顶端中心位置的风速廓线,并使用边界层外缘风速Ul和边界层厚度δ(边界层厚度δ为风速达到0.99Ul时对应的高度)对测量结果进行了无量纲化。实验中Uf=16m/s为来流自由风速,粗糙元高度和宽度相等,h=b=0.01m。图3和图4分别给出了不同w/b值时模拟得到的粗糙元之间和粗糙元顶端中心位置的无量纲风速U/Ul与实验结果对比,可以看出吻合程度较好。
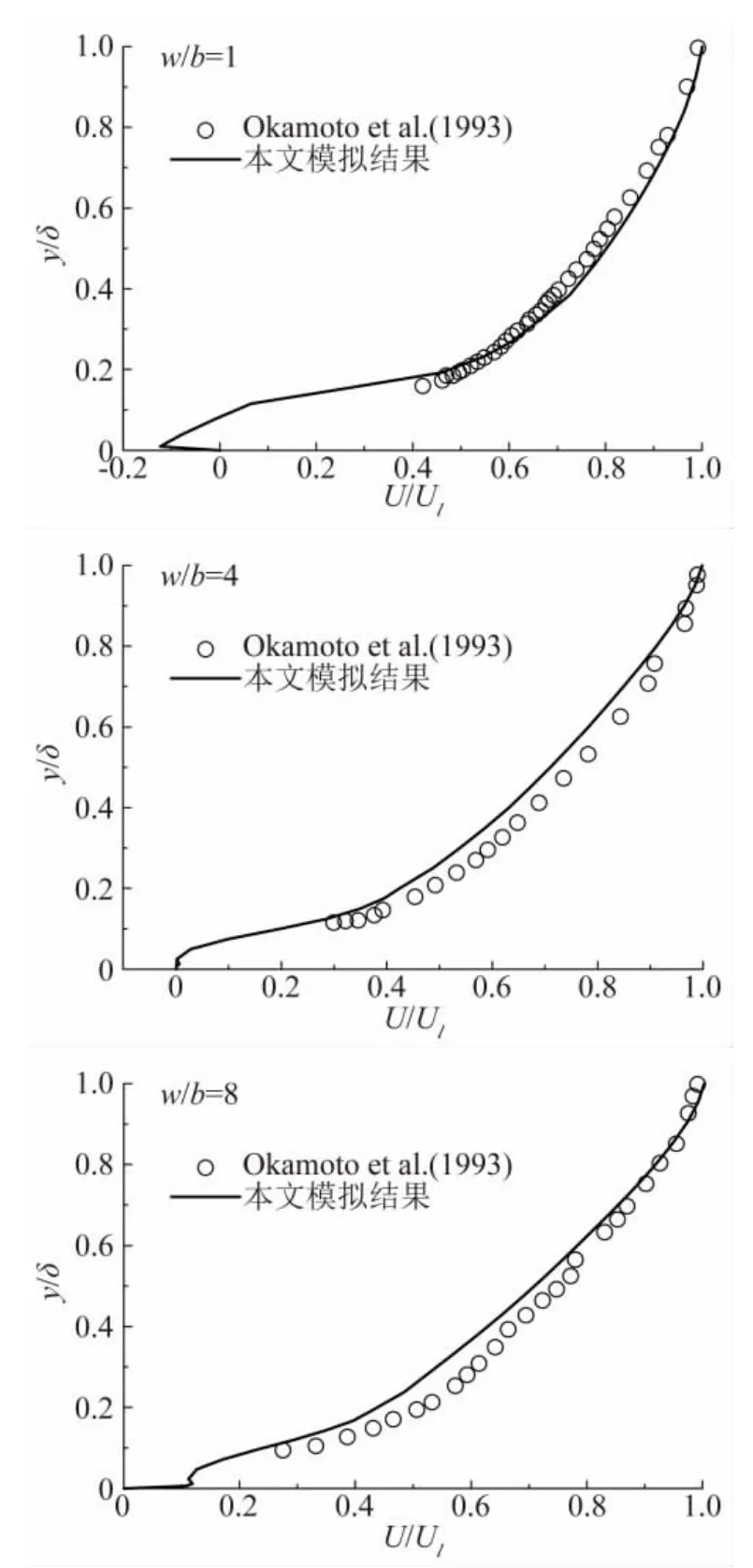
图3 粗糙元之间的风速廓线Fig.3 Mean steamwise velocity profile at cavity between adjoining roughness elements
从图3可以看出,w/b=1时,粗糙元之间中心位置的近壁面风速为负值,表明此处风场与来流方向相反;w/b=4时,粗糙元之间中心位置近壁面风速十分接近0;w/b=8时,粗糙元之间中心位置近壁面风速为正值,表明此处风场与来流方向相同。说明粗糙元分布的越稀疏,粗糙元之间近地面的风速受粗糙元的阻碍作用越弱。从图4可以看出,w/b=1、4、8时,粗糙元顶端的风速廓线在贴近粗糙元顶端很薄的一层高度内近乎水平地快速增大;w/b=8时,y/δ≈0.15高度处的风速廓线稍显凸出,说明此处风速增大的有些超前于这个高度应有的风速。
图5给出的是横截面高度与宽度相等的横肋粗糙元在不同分布密度时,相邻粗糙元之间的流线图。
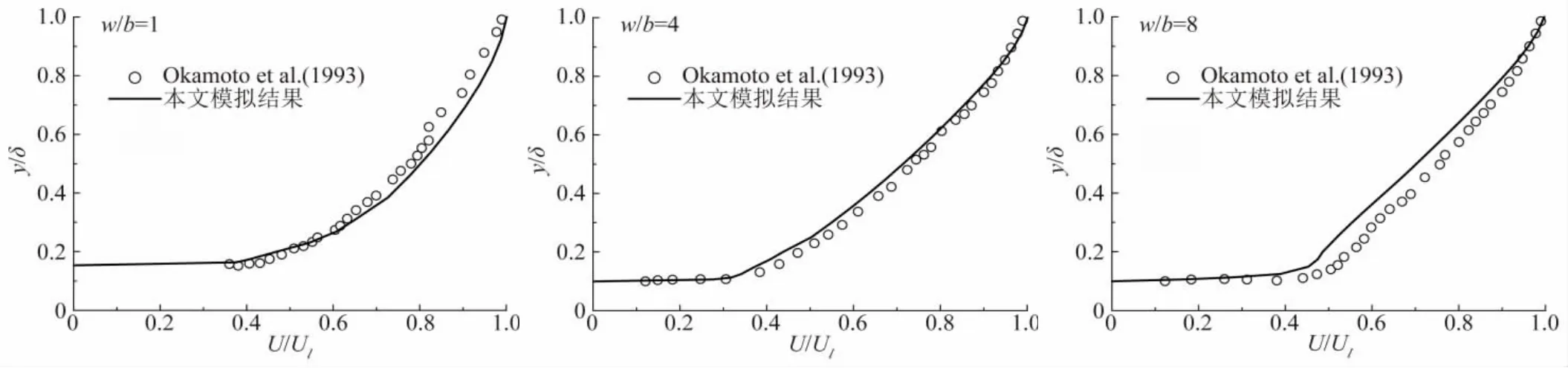
图4 粗糙元顶端的风速廓线Fig.4 Meanstreamwise velocity profile at crest of roughness element
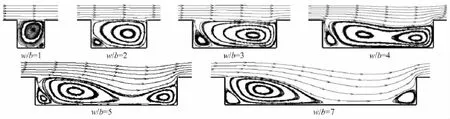
图5 不同w/b值时粗糙元之间的流线图Fig.5 Streamline pattern between adjoining roughness elements with differentw/b
从图5可以看出,近壁面流线遇到粗糙元的时候会与底面发生分离,在粗糙元两侧形成不对称的旋涡。w/b<7时,随着粗糙元分布密度减小,流线涡的形态逐渐发生变化。w/b=1时,粗糙元之间仅有一个占满粗糙元之间空间的主涡;w/b=2、3时,前一个粗糙元的右下角出现一个较小的旋涡;w/b=4时,主涡开始分离;w/b=5时,主涡几乎完全分离,分离部分在后一个粗糙元的左下角形成一个小旋涡;w/b=7时,主涡完全分离,流线涡的形态已经达到稳定。分离后的主涡长度约为4倍的粗糙元高度,越过粗糙元的流线重新附着回底面的位置约在背风面后4.7h的位置,这与Leonardi等[7]和Cui等[16]分别通过直接数值模拟(DES)和大涡模拟(LES)得到的结论十分接近。
3.2 横肋粗糙表面的阻力
固定粗糙元宽度b=0.015m,通过改变w/b值和h/b值研究横肋粗糙元表面特征参数对阻力的影响。雷诺数Re=5000。
3.2.1 摩擦阻力和形状阻力
横肋粗糙表面的阻力包括摩擦阻力ff和形状阻力fP两部分:

摩擦阻力是空气的动力粘度与近壁面空气的速度梯度的乘积:
本研究针对茶尺蠖分别采取了3种诱捕器进行诱捕试验,筛选最适合鄂东南茶区茶园性诱杀虫平台,确定最佳投放间距和高度,以供茶叶生产管理参考。

其中ρ=1.225kg/m3,为空气密度。
对摩擦阻力进行无量纲化,用〈ff〉表示:

图6给出的是四种w/b值下,h/b=2/3、1、4/3和5/3时单位长度λ内的摩擦阻力分布规律。w/b=3时,x/b=1.5~2.5之间为粗糙元所在位置;w/b=4时,x/b=2~3之间为粗糙元所在位置;w/b=5时,x/b=2.5~3.5之间为粗糙元所在位置;w/b=7时,x/b=3.5~4.5之间为粗糙元所在位置。
从图6可以看出,不同w/b值时单位长度内的摩擦阻力具有相似的分布规律。粗糙元迎风面和背风面两侧的摩擦阻力呈现跳跃式的差异。摩擦阻力在粗糙元顶端的迎风一侧达到最大值,然后迅速减小。w/b值越大,摩擦阻力达到的最大值也越大。
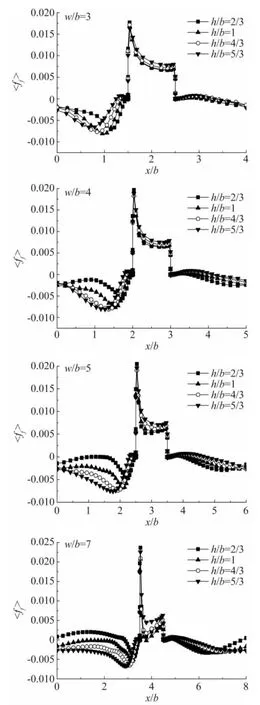
图6 单位长度内摩擦阻力的分布规律Fig.6 Distributions of skin friction drag in the vicinity of a roughness element
w/b=3时,粗糙元背风面之后到粗糙元迎风面之前的摩擦阻力呈现缓慢的先增大后减小,然后在粗糙元迎风面之前显著增大的变化趋势。w/b=4时,粗糙元背风面之后的摩擦阻力增大减小后开始出现并不十分明显的恢复增大的趋势,这是由于粗糙元间距的增大,近地表风场受粗糙元阻碍作用减弱而开始恢复且h/b值越小,这种恢复趋势越明显。随着w/b值的增大,粗糙元背风面之后的摩擦阻力增大减小后恢复增大的趋势越来越明显。h/b值主要影响的是粗糙元之间底面的摩擦阻力。粗糙元背风面之后有一段长度约为2倍粗糙元高度的摩擦阻力减小区,从图6中可以看出,h/b值越小,减小区的长度越短,减小区之后摩擦阻力恢复增大得越快,恢复的摩擦阻力值也越大。
形状阻力为粗糙元迎风面和背风面形成的压力差,由迎风面和背风面的压强差沿粗糙元高度积分得到,单个粗糙元产生的形状阻力用fp表示:
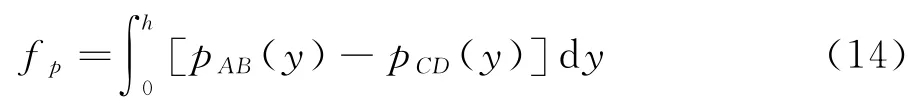
其中,pAB(y)与pCD(y)分别为图1中AB面(即迎风面)和CD面(即背风面)任意高度的压强。
对形状阻力进行无量纲化,用〈fp〉表示:
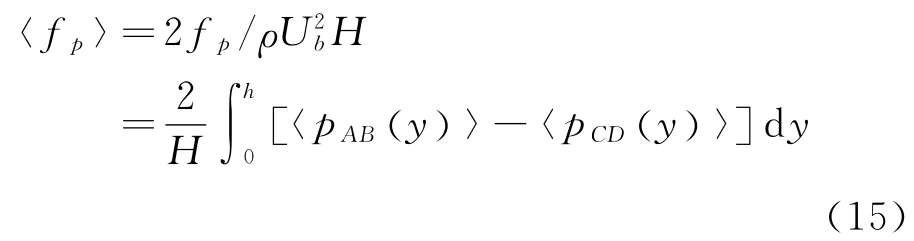
从图7可以看出,不同w/b值时粗糙元迎风面和背风面的压强分布具有相似的变化规律。粗糙元迎风面的压强整体大于背风面,且迎风面压强随高度的增加变化比较剧烈,背风面压强相比之下则变化比较平缓。w/b=3、4时,粗糙元迎风面压强在y/h=0-0.9之间先减小后增大,在y/h=0.4附近达到最小值,在y/h=0.9-1之间急剧减小;w/b=5、7时,粗糙元迎风面压强在y/h=0-0.35之间缓慢减小,在y/h=0.35-0.7之间缓慢增大,在y/h=0.8-1.0之间急剧减小。随着w/b值的增加,迎风面y/h=0-0.8之间的压强变化越来越平缓。h/b值越大,粗糙元迎风面的压强变化越剧烈,背风面的压强整体越大。
3.2.2 粗糙表面的平均阻力
平均摩擦阻力是将单位长度λ内的摩擦阻力积分后求平均得到:

平均形状阻力由单位长度内粗糙元迎风面与背风面的压力差除以单位长度λ给出:
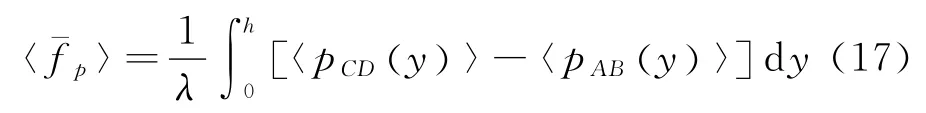
平均总阻力为平均摩擦阻力与平均形状阻力之和:

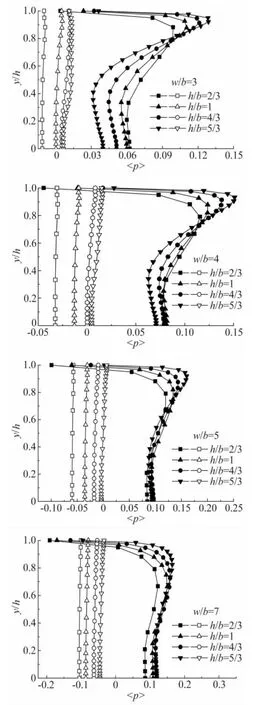
图7 粗糙元迎风面和背风面的压强分布(实心符号表示迎风面压强,空心符号表示背风面压强)Fig.7 Distributions of pressure along the two vertical walls of a roughness element(filled marks stand for the pressure of windward side and empty marks stand for the pressure of leeside)
图8(a)给出了粗糙元高宽比h/b=1时,平均摩擦阻力〈f-f〉、平均形状阻力〈f-p〉和平均总阻力〈f-〉随w/b值的变化规律;图8(b)、(c)、(d)分别给出了h/b=2/3、1、4/3、5/3时,〈f-f〉、〈f-p〉和〈f-〉分别随w/b值变化规律。
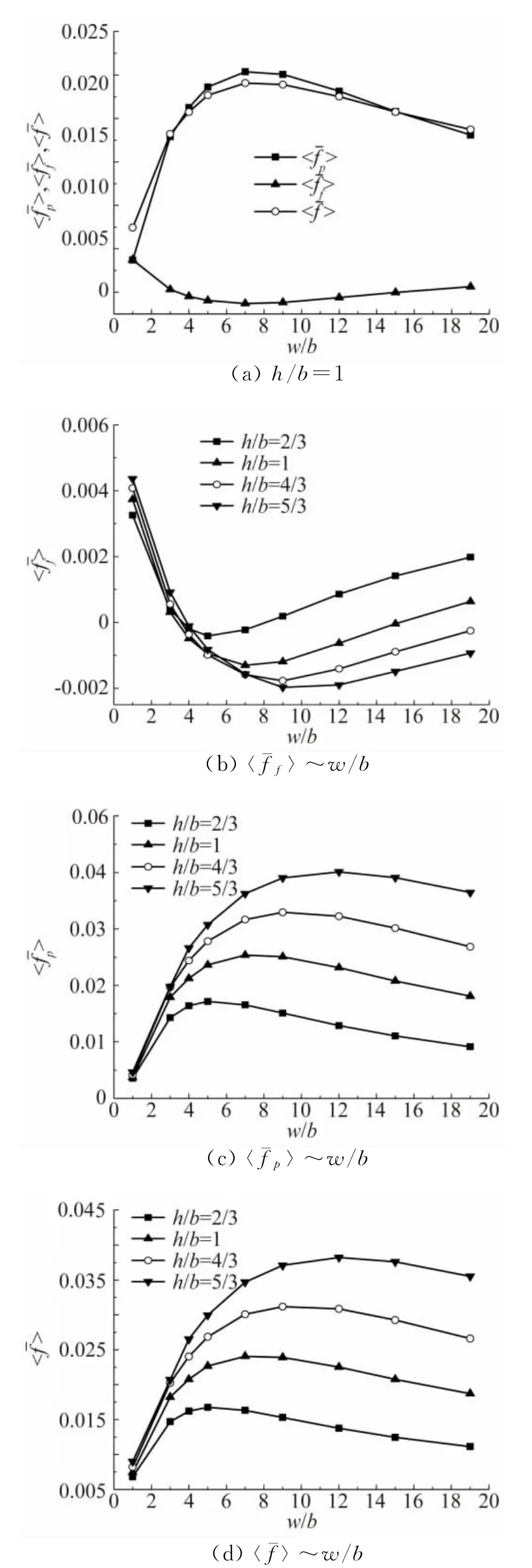
图8 平均阻力随w/b值变化曲线Fig.8 Dependence of the mean resistance onw/b
从图8(a)可以看出,粗糙元高度h与宽度b相等时,随着w/b值的增加,平均摩擦阻力先减小后增大,平均形状阻力和平均总阻力先增大后减小,与Furuya等[6]的实验结果以及Leonardi等[7]的直接数值模拟(DNS)结果一致。w/b=1时,平均摩擦阻力与平均形状阻力大小几乎相等,3<w/b<19时,平均形状阻力远远大于平均摩擦阻力,平均形状阻力起主要作用。w/b=7时,平均摩擦阻力取得最小值,平均形状阻力和平均总阻力取得最大值,这与Leonardi等[7]直接数值模拟(DNS)得到的结论相同。根据图8(a)平均摩擦阻力、平均形状阻力和平均总阻力随w/b值的变化曲线可以看出,如果w/b值无限趋近于0或者正无穷大,也就意味着粗糙表面的形态就无限接近平坦表面,那么横肋粗糙表面的平均形状阻力近乎为0,平均摩擦阻力无限接近平坦表面的平均摩擦阻力,平均总阻力几乎等同于平均摩擦阻力,摩擦阻力起主要作用。
从图8(b)、(c)、(d)可以看出,h/b=2/3、h/b=1、h/b=4/3和h/b=5/3时,平均摩擦阻力随w/b值先减小后增大,平均形状阻力和平均总阻力随w/b值先增大后减小,说明h/b值变化并不改变平均摩擦阻力、平均形状阻力和平均总阻力随w/b值的变化趋势。对平均摩擦阻力,1<w/b<4时,不同h/b值的平均摩擦阻力大小非常接近;9<w/b<19时,h/b值越大,平均摩擦阻力越小。对平均形状阻力和平均总阻力,w/b=1时,不同h/b值的平均形状阻力和平均总阻力大小非常接近,2<w/b<19时,h/b值越大,平均形状阻力和平均总阻力越大。h/b=2/3时,平均总阻力在w/b=5时取得最大值,此时粗糙元的间距高度比w/h=7.5;h/b=1时,平均总阻力在w/b=7时取得最大值,此时w/h=7;h/b=4/3时,平均总阻力在w/b=9时取得最大值,此时w/h=6.75;h/b=5/3时,平均总阻力在w/b=12时取得最大值,此时w/h=7.2。可以发现,h/b值增大,平均总阻力取得最大值时对应的w/b值也增大,但w/h值始终徘徊在7左右,这说明粗糙元的间距高度比w/h是横肋粗糙表面的关键特征参数,横肋粗糙表面的平均总阻力在w/h=7时取得最大值。
4 总 结
本文使用雷诺应力模型(RSM)模拟横肋粗糙表面流动,得出以下结论:
1)平均摩擦阻力随w/b值的增大而先减小后增大,平均形状阻力和平均总阻力随w/b值先增大后减小,h/b值的变化不改变平均摩擦阻力、平均形状阻力和平均总阻力随w/b值的变化趋势。
2)h/b值越小,平均摩擦阻力整体越大,平均形状阻力和平均总阻力整体越小;h/b值越大,平均摩擦阻力整体越小,平均形状阻力和平均总阻力整体越大。h/b值增大,平均总阻力取得最大值时对应的w/b值也增大。
3)粗糙元的间距高度比w/h是横肋粗糙表面的关键特征参数,横肋粗糙表面的平均总阻力在w/h=7时最大。
[1]Dai Gance,Fan Zihui,Wang Guiren.Flow resistance in Repeated-Rib tube[J].Journal of East China Institude of Chemical Technology,1989,15(3):299-304.(in Chinese)戴干策,范自晖,王归仁.横肋管中的流动阻力[J].华东化工学院学报,1989,15(3):299-304.
[2]Krogstad P,Andersson H I,Bakken O M,et al.An experimental and numerical study of channel flow with rough walls[J].Journal of Fluid Mechanics,2005,530:327-352.
[3]Lee S H,Sung H J.Direct numerical simulation of the turbulent boundary layer over a rod-roughened wall[J].Journal of Fluid Mechanics,2007,584:125-146.
[4]Djenidi L,Antonia R A,Amielh M,et al.A turbulent boundary layer over a two-dimensional rough wall[J].Experiments in Fluids,2008,44(1):37-47.
[5]Volino R J,Schultz M P,Flack K A.Turbulence structure in a boundary layer with two-dimensional roughness[J].Journal of Fluid Mechanics,2009,635:75-101.
[6]Furuya Y,Miyata M,Fujita H.Turbulent boundary layer and flow resistance on plates roughened by wires[J].Journal of Fluids Engineering,1976,98(4):635-643.
[7]Leonardi S,Orlandi P,Smalley R J,et al.Direct numerical simulations of turbulent channel flow with transverse square bars on one wall[J].Journal of Fluid Mechanics,2003,491:229-238.
[8]Leonardi S,Orlandi P,Djenidi L,et al.Structure of turbulent channel flow with square bars on one wall[J].International Journal of Heat and Fluid Flow,2004,25(3):384-392.
[9]Leonardi S,Orlandi P,Antonia R A.Properties of d-and k-type roughness in a turbulent channel flow[J].Physics of Fluids(1994-present),2007,19(12):299-304.
[10]Okamoto S,Seo S,Nakaso K,et al.Turbulent shear flow and heat transfer over the repeated two-dimensional square ribs on ground plane[J].Journal of Fluids Engineering,1993,115(4):631-637.
[11]Perry A E,Schofield W H,Joubert P N.Rough wall turbulent boundary layers[J].Journal of Fluid Mechanics,1969,37(02):383-413.
[12]Ashrafian A,Andersson H I,Manhart M.DNS of turbulent flow in a rod-roughened channel[J].International Journal of Heat and Fluid Flow,2004,25(3):373-383.
[13]Nie S Y,Gao Z H,Huang J T.Differential Reynolds stress model for shock &separated flow[J].Acta Aerodynamica Sinica,2012,30(1):52-56.(in Chinese)聂胜阳,高正红,黄江涛.微分雷诺应力模型在激波分离流中的应用[J].空气动力学学报,2012,30(1):52-56.
[14]Zhang Y,Liu S Y,Wang B G.Application of the Reynolds stress model to the calculation of three-dimensional turbulent flow-field[J].Journal of Aerospace Power,2005,20(4):572-576.(in Chinese)张雅,刘淑艳,王保国.雷诺应力模型在三维湍流流场计算中的应用[J].航空动力学报,2005,20(4):572-576.
[15]Gatski T B,Jongen T.Nonlinear eddy viscosity and algebraic stress models for solving complex turbulent flows[J].Progress in Aerospace Sciences,2000,36(8):655-682.
[16]Cui J,Patel V C,Lin C L.Large-eddy simulation of turbulent flow in a channel with rib roughness[J].International Journal of Heat and Fluid Flow,2003,24(3):372-388.
Research on wind resistance characteristics of transverse rod-roughened surface
Li Bing,Jiang An,Wu Jianjun*
(Key Laboratory of Mechanics on Disaster and Environment in Western China with the Ministry of Education,School of Civil Engineering and Mechanics,Lanzhou University,Lanzhou 730000,China)
The wind field above transverse rod-roughened surface is investigated using the Reynolds stress model(RSM).The RSM abandons Boussinesq hypothesis that the Reynolds stress has linear relationship with mean velocity gradient.The RSM is more realistic because the convection and diffusion effects of Reynolds stress are considered.The pitch width ratiow/b、aspect ratioh/band pitch height ratiow/hare regarded as the main characteristics parameters of transverse rod-roughened surface to study the effect of roughness elements distribution density and cross section size on rough surface resistance.Numerical results indicate that the mean frictional resistance first decreases then rises with the increasing ofw/b,while the variation of mean form resistance and mean skin resistance show contrary trends and the variation ofh/bhas nothing to do with these trends.Thew/bcorresponding to the maximum mean skin resistance increases withh/b,and thew/hcorresponding to that keeps around 7.It suggests that the pitch height ratio is the key parameter of transverse rod-roughened surface and the maximum skin resistance occurs atw/h=7.
transverse rod roughness;frictional resistance;form resistance;skin resistance
O359;X169
Adoi:10.7638/kqdlxxb-2015.0025
0258-1825(2016)04-0517-07
2015-03-02;
2015-05-14
国家自然科学基金委创新研究群体(11421062);国家自然科学基金重大计划项目(91325203);国家自然科学基金项目(11472121)
李冰(1988-),男,河南郑州人,硕士研究生,研究方向:风沙物理学.E-mail:lbing2012@163.com
武建军*(1964-),E-mail:wujjun@lzu.edu.cn
李冰,江岸,武建军.横肋粗糙元地表的风场阻力特征研究[J].空气动力学学报,2016,34(4):517-523.
10.7638/kqdlxxb-2015.0025 Li B,Jiang A,Wu J J.Research on wind resistance characteristics of transverse rod-roughened surface[J].Acta Aerodynamica Sinica,2016,34(4):517-523.
