一种新的计算非稳态流动的自适应无网格方法

王 亮，许厚谦，吴 伟，薛 锐

（南京理工大学能源与动力工程学院，江苏南京 210094）

一种新的计算非稳态流动的自适应无网格方法

王 亮＊，许厚谦，吴 伟，薛 锐

（南京理工大学能源与动力工程学院，江苏南京 210094）

基于带权点填充布点方法，结合指定流场参数梯度的分布，提出了一种新的无网格自适应方法计算非稳态问题。该方法的自适应探测器E由节点的权重和参数梯度组成。使用自适应探测器识别出加密或者粗化的区域，形成加密空腔和粗化空腔，然后重新填充布点。新节点的权重由自适应探测器E结合该处的梯度大小通过预测－校正迭代算法计算得到。另外，由于参数梯度在激波附近波动范围比较大，所以新节点的权重存在最大值和最小值。首先对预先设置压强梯度的流场区域进行自适应布点，并与传统自适应布点结果进行对比，点云分布图显示所提自适应方法重新生成的点云结构疏密分布更加合理。进一步，将此自适应方法应用于Riemann问题和激波碰撞圆柱问题，计算结果表明该方法可以在节点数目较低的情况下显著提高运动激波的分辨率。在激波碰撞圆柱问题中，比较了使用自适应算法和非自适应算法得到相当的结果所使用时间，前者是后者的20.6%，因此该自适应算法在计算效率方面也具有较大的优势。

无网格方法；自适应方法；激波；点云

0 引 言

在计算流体力学中，无网格方法越来越受到关注［14］，这主要是由于无网格方法空间离散相对灵活，易于处理边界较为复杂或存在复杂边界变形的流动问题。无网格方法空间离散是将计算区域划分为一系列的节点，节点之间无线段相连，避免了多边形单元的生成，减少了存储计算信息所占用的内存空间。然而无网格方法也存在一定的缺陷：首先是其精度相对于网格方法较低，当节点间距过疏时，计算结果误差较大甚至无法分辨激波间断；另外是计算效率较低，主要是由于形函数的计算涉及多次矩阵求逆、矩阵相乘等运算，而且每个离散单元与周围单元间的通量计算个数（二维空间，一般大于等于6）也大于网格方法（二维空间，一般为3或者4）。所以，研究无网格快速算法是现在无网格方法研究重点之一。

自适应技术是一种被广泛使用于提高计算效率的方法，特别是在网格方法中［5－7］。在无网格方法中，大量学者［8－12］也对自适应技术做作了较多的研究：马志华［13］和蒲赛虎［14］根据流场中压强梯度的大小，在原有节点的基础上进行快速的局部加密或者粗化；马志华［15］随后又基于移动节点的思想提出了点云自适应移动技术，该方法将流场中的离散点向梯度较大的区域聚集，主要适用于稳态问题；倪国喜等［16］根据流场参数的分布，结合Voronoi图方法对整个计算区域重新布点，清晰展现了点云基于参数大小的自适应分布；Jun等［17］采用再生核粒子法（RKPM）自身具有多尺度分辨率的特性，将解分为高阶模态和低阶模态，在大梯度的区域利用高阶模态过滤器进行精细处理；Liu等［18］结合事后误差估计和Voronoi图对流场进行加密。

本文基于梯度准则和带权点填充布点技术［19］提出了一种新的无网格自适应方法。该方法采用流动参数梯度大小和节点权重相结合的自适应探测器对计算流场进行探测，形成加密空腔或粗化空腔。点云加密或粗化是在完全摒弃原有点云的基础上重新生成的，充分地体现了参数的不均匀分布对点云结构的影响，简单灵活，稳态和非稳态问题均适用。为了验证所提无网格自适应方法在自适应区域内点云分布的合理性，本文首先对预先设置压强梯度的流场进行自适应布点，然后使用该方法分别计算非稳态的黎曼问题和激波碰撞圆柱问题。

1 控制方程

本文采用无黏Euler控制方程，在直角坐标系中可表示为：

式中，U是守恒变量，F及G为无粘通量，分别为：

式中，ρ为密度，u、v为运动速度X和Y方向的分量，p为气体压强，E为单位质量总能。状态方程采用刚性气体状态方程。

式中，P∞和γ分别是压力扩展系数和气体比热比，气体为空气时，P∞＝0，γ＝1.4。

2 数值方法

本文采用最小二乘方法逼近空间导数，基函数采用一阶线性函数，其具体形式如下：

以流场中某一点i为例，其卫星点个数为N，此点云中N＋1个点均满足式（3）。所以可以通过一定的运算得到如下矛盾方程组：

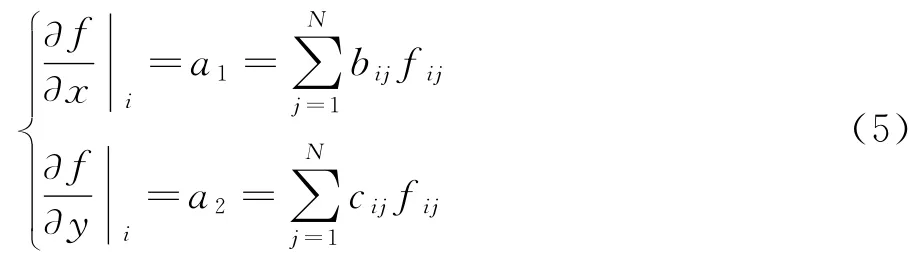
则，控制方程（1）中的通量项可以表示为：

HLLC是一种近似求黎曼解的方法，由Toro等［20］对Harten及Lax等［21］提出的HLL方法进行改进所得。吴伟［19］将该方法引入到无网格方法中，计算结果中激波的分辨率比较高。所以本文采用文献［19］中的HLLC格式计算数值通量。

3 自适应技术

3.1 带权点填充布点技术概述

带权点填充布点技术是由吴伟［19］提出的一种新的无网格布点方法。该方法的主旨是赋予每一离散节点一个实数的权重，其物理意义可以理解为以该点为圆心，权重大小为半径的圆球面。带权点填充布点就是将具有相同或不同半径的圆球面填充到计算区域中。在实际操作中，为了加强该方法的灵活可用性，两个相邻的虚拟圆球面之间并不要求严格意义上的相切，即允许部分的相交或相离。其具体的布点过程分为以下几步：

1）根据实际情况，对边界进行均匀或按照某一规则非均匀布点，每一个边界点i的权重ri＝为点i与相邻节点j的距离，N为相邻点的个数；

2）将边界作为初始阵面，向内部填充带权点。以阵面边AB为例，其最佳推进带权点C的权重取两端点A和B权重的平均，通过节点C所在的球面与节点A和B所在的球面相切的原理，得到带权点C的坐标。然后在C点周围寻找现有的带权点，形成候选点链表，经过穿透、交叉等几何判断，删除无效的带权点。最后根据现有带权点与理想推进点的重叠系数大小确定最佳推进点。具体的计算方法见文献［19］。

3）填充布点结束后对内部节点进行Laplace光顺处理，使得流场节点分布更加合理。

3.2 自适应方法

在以上带权点填充布点技术的基础上，本文提出了一种新的自适应布点方法。该方法的自适应探测器采用参数梯度大小与节点权重相结合的方法确定，具体的表达式为：

1）计算流场中每一节点的探测器E的取值，并对整个区域内的探测器值取平均，得到E0，即该流场的自适应基准值。

其中，M为计算域内节点个数。

2）对整个区域内的点进行加密或粗化判断：当ri＞1.1αrmax，Ei＞E0时，将点i标注为加密待删除点；当ri＜0.85βrmax，Ei＜0.1E0时，将点i标注为粗化待删除点。然后分别形成加密空腔和粗化空腔。

3）对形成的空腔进行带权点填充布点。新填充点C的权重采用以下公式计算。

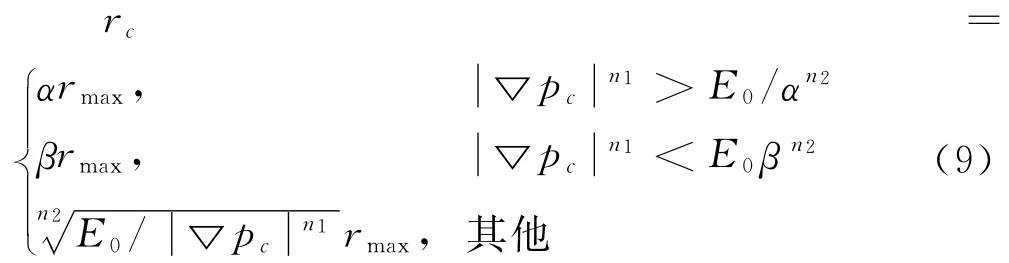
4）填充布点结束后对新增加的内部节点进行Laplace光顺处理，使得流场节点分布更加合理。

4 数值算例

4.1 布点示例

本文首先对预先设置压强梯度值的流场进行自适应布点，以检验采用本文自适应方法重构点云分布的合理性。布点区域为一边长为4的正方形，中心点位于原点（0，0）。其中，本文假设在以中心点为圆心，半径为1的圆形区域内压强梯度值为外部区域的压强梯度值均为零。布点的最大权重为0.1，最小权重为0.0125，E0＝5。图1（a）给出了相应的布点结果，图1（b）给出了采用传统自适应方法［14］的布点结果。由于传统方法是在原有节点的基础上在两节点中心处添加新节点或者删除新增加的点，所以要进行多次自适应布点才能使得大梯度区域点的权重达到0.0125。通过观察可以发现传统方法的节点分布呈现阶梯型，节点的自适应相对简单，无法准确地与梯度的分布相吻合，冗余节点的产生是无法避免的，而采用本文的方法进行自适应布点时，节点疏密过渡更加自然，与梯度的分布情况更加吻合，能够最大程度的减少或避免冗余节点的产生。

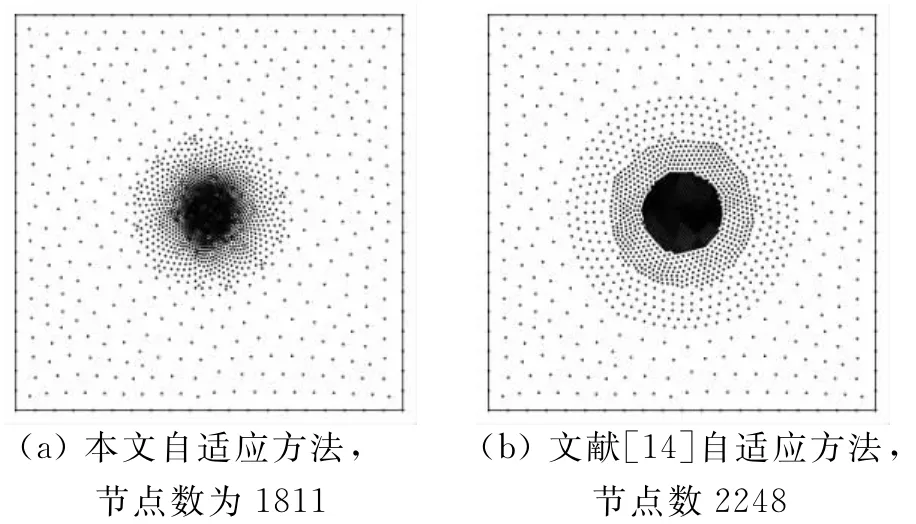
图1 自适应布点结果Fig.1 Adaptive point distributions

4.2 Riemann问题

Riemann问题是经典的非稳态激波管问题。激波管内放置一薄膜，薄膜两侧分别充满不同状态的空气。本文采用二维轴对称模型进行求解。空气的初始状态值为：

0.0≤x≤0.5：

ρ＝1.0，u＝0.0，p＝1.0

0.5＜x≤1.0：

ρ＝0.125，u＝0.0，p＝0.1

t＝0时刻，薄膜破裂，由于密度压力的不同，空气开始流动。

初始时刻，计算域内均匀分布的无网格节点数为1234，如图2（a）所示，采用非自适应算法得到的计算结果如图3所示，激波的捕捉精度较低，厚度较大，无法达到计算要求。所以本文采用自适应无网格方法对计算域内点云进行实时加密及粗化。对于该算例，自适应探测器公式中的流场参数梯度取密度梯度。图2（b）给出了t＝0.2时刻计算域内自适应点云分布图，在密度变化较为剧烈的区域，点云分布的很密，并且左侧的膨胀波区域点云分布由疏到密，右侧强激波附近点云分布密集，对应的激波管内密度及压力分布曲线如图3所示。比较自适应结果和非自适应结果，可以发现激波的分辨率得到了很大的改善，而且自适应结果与解析解吻合的较好。该算例说明本文的自适应方法可以准确捕捉非定常流动中的简单运动激波。

图2 计算域内t＝0.0和t＝0.2时刻节点分布Fig.2 Gridless points distributions att＝0.0andt＝0.2

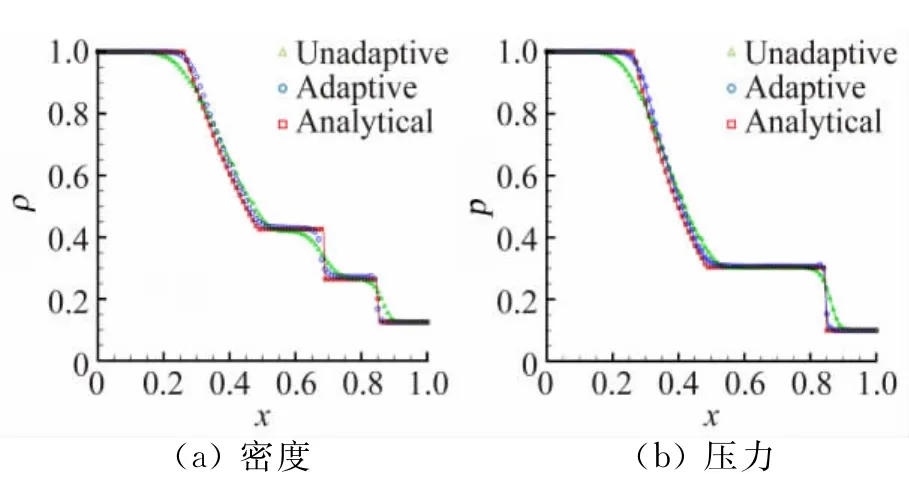
图3 在t＝0.2时刻的压力与密度分布曲线Fig.3 Curves of pressure and density att＝0.2

4.3 瞬时激波碰撞圆柱

在以上计算的基础上，本算例给出了自适应无网格方法在二维非稳态无黏圆柱绕流问题中的应用。计算区域为长度L＝6.0，高度是H＝3.0的管道，圆柱位于管道中心处，半径为1.0。管道内初始激波的位置在圆柱左侧0.45处，激波左侧流场状态为：ρ＝2.667，u＝1.479，v＝0.0，p＝4.5；激波右侧流场状态为：ρ＝1.0，u＝0.0，v＝0.0，p＝1.0。计算采用的初始无网格节点数为4703，均匀分布。

图4给出了随着时间的推进，计算域内的压力等值线图以及对应无网格点云分布的变化。观察发现点云动态分布合理，在激波附近一直比较密，激波运动过后的区域点云被及时粗化，激波厚度始终较小，由此可以说明本文的自适应算法可以实时捕捉较为复杂的运动激波。图5给出了不采用自适应方法，计算域内较密集地均匀分布76389个无网格节点时，计算得到的t＝1.2时刻压力等值线图。比较发现两种方式得到的激波位置及强度吻合的很好，激波分辨率很高。比较两种算法所使用的时间，自适应算法所使用的时间只占直接采用较密节点计算的20.6%，所以本文自适应算法也可以有效提高计算效率。本文计算效率低于文献［14］，这是由于本文自适应点云重构需要耗费较长的时间。然而，比较本文和文献［14］中t＝1.2时刻自适应点云分布图，在激波附近本文点云分布更加紧密，其他区域也相对比较稀疏，说明本文方法可以更加准确地探测到计算域内需要自适应的区域，并对其进行重新布点，使得参数变化较为剧烈的区域内的点云分布更加密集。

图4 在t＝0.9、1.2、1.5时刻的自适应结果（左侧是压力等值线图，右侧是自适应无网格节点分布图）Fig.4 Adaptive results att＝0.9，1.2，1.5（Left：pressure contours，Right：adaptive gridless points distributions）

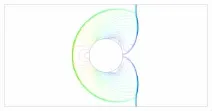
图5 节点总数为76389时，直接计算得到的t＝1.2时刻压力等值线Fig.5 Pressure contours att＝1.2 when the number of gridless points is 76389

5 结 论

在带权点填充布点的基础上，本文结合流场中指定流场参数的梯度分布规律发展出了一种新的自适应无网格方法。该方法在自适应区域重新生成点云，简单，灵活，实用，能够准确求解非定常问题。为验证自适应后节点分布的鲁棒性，首先针对预先设置压强梯度分布的计算域进行了自适应布点，得到的无网格自适应点云分布图显示这种方法能够根据梯度的大小对计算域合理地进行加密或粗化。随后，非稳态的Rimeann问题和瞬时激波碰撞圆柱问题的计算结果显示本文方法能够准确识别激波所在的区域，并能实时捕捉运动激波，而且点云的自适应结果合理，进一步展示了所提自适应方法在非稳态问题计算中的有效性。在瞬时激波碰撞圆柱问题中，本文比较了自适应计算和非自适应计算得到相当的结果所耗费的时间，结果显示自适应算法的计算时间比较小，所以本文的算法是可以较好地提高无网格计算效率的。本文后续的工作将考虑改进点云重构方法以进一步提高自适应计算效率并将该自适应方法应用于求解存在复杂边界变形的多介质流动问题。

［1］Sun Yingdan，Wang Gang，Ye Zhengyin.Extending the AUSM＋－up scheme into the gridless method［J］.Acta Aerodynamica Sinica，2005，4（4）：511－515.（in Chinese）孙迎丹，王刚，叶正寅，等.AUSM＋－up格式在无网格算法中的推广［J］.空气动力学学报，2005，4（4）：511－515.

［2］Hong Luo，Joseph D Baum，Rainald Lhner.A hybrid cartesian grid and gridless method for compressible flows［J］.Journal of Computational Physics，2006，214（2）：618－632.

［3］Ma Zhihua，Chen Hongquan，et al.A new type hybrid algorithm using local gridless techniques［J］.Acta Aerodynamica Sinica，2008，26（03）：344－348.（in Chinese）马志华，陈红全，等.基于局部无网格的混合算法研究［J］.空气动力学学报，2008，26（03）：344－348.

［4］Wu Wei，Xu Houqian，Wang Liang，et al.Numerical simulation for the external combustion of base－bleed projectile using gridless method［J］.Journal of Harbin Institute of Technology，2014，21（3）：95－100.

［5］Kang Hongwen，Gu Xiangqian，Liu Chongjian.Study on weigh functions of adaptive grid technique［J］.Acta Mechanica Sinica，2002，34（5）：790－795.（in Chinese）康红文，谷湘潜，柳崇健.自适应网格技术中的权函数问题研究［J］.力学学报，2002，34（5）：790－795.

［6］Han Zhirong，Lu Zhiliang，et al.Grid adaption for separation flow［J］.Acta Aerodynamica Sinica，2012，1（1）：86－89.（in Chinese）韩志熔，陆志良，郭同庆，等.一种用于分离流动的网格自适应算法［J］.空气动力学学报，2012，1（1）：86－89.

［7］Xu Heyong，Ye Zhengyin，Zhang Weiwei.Numerical simulation of hypersonic flow based on unstructured adaptive grid method［J］.Engineering Mechanics，2012，29（3）：226－229.（in Chinese）许和勇，叶正寅，张伟伟.基于非结构自适应网格技术的高超声速流动数值模拟［J］.工程力学，2012，29（3）：226－229.

［8］Lee，Sangho，Hyo Jinkim，Sukky Jun.Two scale meshfree method for the adaptivity of 3－D stress concentration problems［J］.Computational Mechanics，2000，26（4）：376－87.

［9］You Y，Chen J S，Lu H.Filters，reproducing kernel，and adaptive meshfree method［J］.Computational Mechanics，2003，31（3－4）：316－326.

［10］Lee C K，Zhou C E.On error estimation and adaptive refinement for element free Galerkin method：Part II：Adaptive refinement［J］.Computers and Structures，2004 82（4－5）：429－443.

［11］Rossi R，Alves M K.Recovery based error estimation and adaptivity applied to a modified element－free Galerkin method［J］.Computational Mechanics，2004，33（3）：194－205.

［12］Ma Z H，Hong Q C.Mesh free adaptive algorithm for solving Euler equations on structured grid points［J］.Transactions of Nanjing University of Aeronautics and Astronautics，2005，22（4）：271－275.

［13］Ma Z H，Chen H Q.Simulations of transonic inviscid flows over airfoilsusing meshfree adaptive algorithm［J］.Modern Physics Letters B，2005，19（28－29）：63－66.

［14］Pu S H，Chen H Q.Gridless adaptive method for simulating flows with moving shocks［J］.Aeronautical Computing Technique，2012，42（5）：4－8.（in Chinese）蒲赛虎，陈红全.模拟存在运动激波流场的无网格自适应算法［J］.航空计算技术，2012，42（5）：4－8.

［15］Ma Z，Chen H，Zhou C.A study of point moving adaptivity in gridless method［J］.Computer Methods in Applied Mechanics＆Engineering，2008，197（21）：1926－1937.

［16］Ni G X，Wang R L，Lin Z.Adaptive distribution of particles in a meshfree method［J］.Chinese Journal of Computational Physics，2006，23（4）：419－424.（in Chinese）倪国喜，王瑞利，林忠.无网格方法中粒子分布与自适应研究［J］.计算物理，2006，23（4）：419－24.

［17］Jun S，Im S.Multiple－scale meshfree adaptivity for the simulation of adiabatic shear band formation［J］.Computational Mechanics，2000，25（2－3）：257－266.

［18］Liu G R，Tu Z H.An adaptive procedure based on background cells for meshless methods［J］.Computer Methods in Applied Mechanics ＆Engineering，2002，191（s17－18）：1923－1943.

［19］Wu W.Gridless method for numerical simulation of complex chemical reaction flow field and its application［D］.Nanjing：Nanjing University of Science ＆Technology，2015.（in Chinese）吴伟.复杂化学反应流场数值模拟的无网格方法及应用［D］.南京：南京理工大学，2015.

［20］Toro E F，Spruce M，Speares W.Restoration of the contact surface in the HLL－Riemann solver［J］.Shock Waves Journal，1994，4：25－34

［21］Harten A，Lax P D，Leer B V.On upstream differencing and Godunov－type schemes for hyperbolic conservation laws［J］.SIAM Revision，1983，25：35－6.

A novel gridless adaptive method for simulating unsteady flows

Wang Liang＊，Xu Houqian，Wu Wei，Xue Rui

（School of Energy and Power Engineering，Nanjing University of Science ＆Technology，Nanjing 210094，China）

Based on the weighted－point filling strategy，a novel gridless adaptive method is developed to capture shock waves with high resolutions in unsteady flows.The adaptive indicatorEis the function of the local specified parameter gradients and the weight of points.The refining and coarsening regions are identified by the indicator，and then form refining cavities and coarsening cavities which are filled with new points.Using the predictor－corrector iterative algorithm，the weight of the new point is obtained by the adaptive indicatorEand the local gradient.To prevent the violent change of the point weights with the parameter gradients，the maximum and the minimum are stipulated respectively in the filling process.The proposed adaptive method is firstly used to fill points into the flow field which is set with designated pressure gradient in advance.By comparison with the traditional adaptive result，the sparse and dense distributions of clouds of points are more satisfactory and more reasonable.Further studies are the calculations of Riemann flow and incident shock past a cylinder.The results show that the adaptive method can capture the moving shock waves successfully in the unsteady flow fields with scanty points.For achieving equivalent pressure contours of the flow of the incident shock past a cylinder，the time spent using the presented adaptive method is 20.6%of the conventional unadaptive method，which suggests that it has a definite advantage on the computational efficiency.

gridless method；adaptive strategy；shocks；clouds of points

V211.3

Adoi：10.7638／kqdlxxb－2015.0185

0258－1825（2016）04－0497－06

2015－10－10；

2015－11－26

王亮＊（1989－），男，安徽阜阳人，博士研究生，计算流体力学.E－mail：310082216＠njust.edu.cn

王亮，许厚谦，吴伟，等.一种新的计算非稳态流动的自适应无网格方法［J］.空气动力学学报，2016，34（4）：497－502.

10.7638／kqdlxxb－2015.0185 Wang L，Xu H Q，Wu W，et al.A novel gridless adaptive method for simulating unsteady flows［J］.Acta Aerodynamica Sinica，2016，34（4）：497－502.