《相遇问题》教学设计及反思

谢　涛

【教学内容】

青岛版三年级下册第九单元《信息窗》。

【教学过程】

一、创设情境，导入新课

师：同学们，请看，有这样一个问题：出示：小红每分钟走60米，4分钟从家走到学校。她家到学校有多少米？你会列式解答吗？

生：60×4=240（米）。

师：你是根据什么数量关系列式的?

生：速度×时间=路程。

师：这道题是已知速度和时间，求路程，就要用“速度×时间=路程”。这是我们以前学习的一个物体的运动情况，今天我们就在“速度×时间=路程”这个数量关系的基础上研究两个物体的运动情况。

二、探究交流，学习新知

1.初步理解题意。

课件出示：小红和小明同时从家出发相对而行，小红每分钟走60米，小明每分钟走70米，经过4分钟两人相遇。

师：用你数学的眼光仔细观察，从中你能获得哪些数学信息？

（学生汇报信息）

师：他们是怎么走的呢?

（学生可能说：同时从家出发相对而行，最后相遇了）

师：小红和小明同时从家出发，“同时”你是怎样理解的?

生：同时就是同一时刻。

师：例如小红是7时出发，那小明呢？

生：小明也是7时出发。

师：“相对而行”是什么意思？

生：就是面对着面走。

师：“相遇”是什么意思？

生：碰面了。

师：为了更形象地表示出两人行走的过程，我们还可以找两位同学表演表演，谁来？

师：看着这些信息，根据你们的理解，想一想该怎样表演呢？你们两人可以先商量商量。下面的同学同桌两人商量商量。

师：商量好了吗？我说开始，你们再走，相遇以后握一握手，其他同学当评委，看他们在表演时能不能准确地表示出题目中的信息。

（组织学生表演，其他学生评价。重点关注“同时”、相对而行”、“相遇”以及“行走速度”等）

2.根据信息，发现提出数学问题。

师：通过表演，同学们对题中的信息有了比较深刻的理解。根据这些信息，你能提出什么数学问题？

（学生可能提出：小红走了多少米？小明走了多少米？这样的问题直接解答。还有学生提出：他们两家相距多少米？）

师：同学们提出了这么多有价值的问题，今天我们就来解决刚才那位同学提出的问题，课件出示：他们两家相距多少米？

3.画线段图，理解题意。

师：这个问题中的信息比较多，并且数量之间的关系不易发现，为了更清晰、简洁地表示出题目中的信息和问题，我们还可以画线段图帮助我们理解题意。

师生共同完成线段图：用两个点分别表示小红家和小明家，小红朝这个方向走，（画箭头），小明呢？（画箭头），小红每分钟走60米，小明每分钟走70米，经过4分钟两人相遇，相遇的地点离谁家近些？（小红家）在这儿相遇了，小红走了几分钟？（4分钟），我们就要把这一段平均分成4份，这样的一份就表示小明每分钟走60米，小明走了几分钟？（4分钟），同样，也把这一段平均分成4份，这样的一份就表示小明每分钟走70米，问题标在哪里？标上问题。

师：看着线段图，你能完整地说一说题目的意思吗？

4.尝试解决，汇报交流。

（1）自主尝试。

教师边指题边说：要求他们两家相距多少米，我们应该怎么想呢？要先求什么？再求什么？同学们可以结合线段图想一想。

（学生尝试完成，教师巡视、指导，收集学生作业）

（2）汇报交流。

（第一种方法的侧重点是两家的距离与两人4分钟走的路程和之间的关系；第二种方法的侧重点是速度和的问题）

展示学生的第一种方法：60×4+70×4。学生结合线段图说思路：先求出小明和小红各走了多少米，再求他们一共走了多少米。

师：这位同学不仅做得好，说得也很条理。大家听明白了吗？

教师小结：求两家相距多少米？我们可以先求出小红和小明4分钟各走了多少米，再求出他们一共走了多少米。也就是用“小红走的路程+小明走的路程=总路程”，我们一起把算式写下来。

展示学生的第二种方法：（60+70）×4。

生：（60+70)×4是先求他们两人一分钟共走了多少米，再求出他们4分钟一共走了多少米。

师：大家明白吗？从你疑惑的眼神中，老师看出有的同学还不大明白，为了让大家理解得更透彻，咱们用课件演示一遍。请看，多媒体演示，强化学生对“速度和”的理解，小红每分钟走多少米？（60米）小明呢？（70米）他们两人1分钟共走多少米？（130米）两人1分钟共走的路程就是两人的速度和。第2分钟呢？（130米）第3分钟呢？（130米）第4分钟？（130米）共走了几个130米？（4个）。我们可以先求出两人1分钟共走了多少米，再求出两人4分钟一共走了多少米。也就是用“速度和×相遇时间=总路程”，按照这种思路，该怎样列式呢？

生：(60+70)×4。

教师指算式，这里的60+70表示什么？（两人1分钟共走了多少米，速度和）

（3）检验。

师：解答完问题，不要忘记检验，你在解决问题的时候有什么好的检验方法？

生：回过头仔细检查。

师：回头看。

生：如果有两种方法，可以用一种方法检验另一种方法。

师：这道题就有两种方法，请大家检验检验。不要忘记写上答。

（4）比较、质疑。

师：同学们真聪明，想出了两种方法解决这个问题，仔细观察、比较这两种方法，有什么不同的地方？

（学生说不同点）

教师小结：两种方法的思路不同，在解决这个问题时我们可以先分别求出每个人所走的路程，再加起来。还可以先求出两人的速度和，再乘以相遇时间。这就是我们研究的相遇问题。

5.回顾过程，总结方法。

师：回顾我们解决问题的过程，当我们遇到一个实际问题时，要先审题，再分析、解答，最后检验。（板书：审题 分析列式解答 检验作答）

三、综合应用，提高能力

1.只列式，不计算。

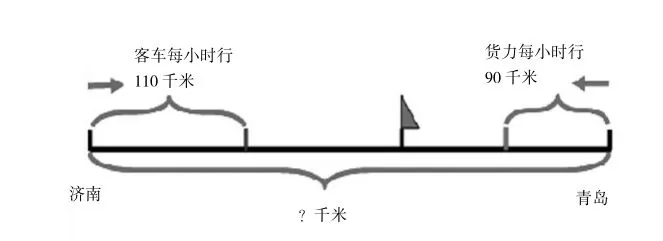
2.两个修路队合修一条公路，各从一端同时向中间施工。第一队每天修300米，第二队每天修200米，经过6天正好修通。这条公路长多少米？

师：请大家认真读题，可以多读几遍题，第1题要图文结合读，第2题有困难的同学可以画一画线段图，想好后做在作业纸上，只列出算式就可以了，不用计算。

（收集学生作业，展示汇报两种方法）

针对第2题，教师引导学生沟通联系：这道修路的问题和刚才解决的问题有什么相同的地方？

生：它们都是从两个地方同时相对前进，最后相遇，都是求总路程。

生：解决问题的思路是一样的。

教师总结：同学们，像刚才我们研究的两个人或两种事物同时从两地出发，相对而行，最后相遇，求两地相距多少的问题，都是我们今天研究的相遇问题，解决这种问题的数量关系是一样的。

3.选一选。

中午放学后，小刚和小丽同时从学校出发。小刚向东走，每分钟走60米；小丽向西走，每分钟走50米。经过3分钟，两人相距多少米？

师：要求两人相距多少米？正确的算式是哪个？让学生口答，并讲出理由。第②个算式表示什么意思？

4.智慧乐园。

师：我们一起走进智慧乐园看看吧。

课件出示：

小华和小亮在环形跑道上跑步，两人从同一地点同时出发，反向而行。小华每秒跑4米，小亮每秒跑6米，经过40秒两人相遇。环形跑道长多少米？

师：他们是怎样跑的？两人从同一地点同时出发，反向而行。可以用手势表示。请自己解答在练习本上。

（组织学生交流方法和想法）

师：请同学们思考一个问题：在这种环形跑道上，他们从同一地点同时出发，反向而行，最后相遇，我们在求环形跑道长多少米的时候，为什么用的方法和刚才研究的相遇问题的方法是一样的？

（我们结合线段图看一看）

教师总结：通过这节课的学习，我们知道了无论是刚才研究的两个人或两个物体同时从两地出发，相对而行，最后相遇的问题，还是环形跑道上两个人同时从同一地点出发，反向而行，最后相遇的问题，我们都可以用这种思路来解决。

四、总结反思、畅谈收获

【课后反思】

1.创造使用教材，合理选取素材。

本课在设计时充分领会教材编写意图，掌握教材的基本结构但又不为教材所约束。教材中的素材是“小萍和小明同时从家去栈桥，小萍每分钟走65米，小明每分钟走75米，经过6分钟两人在栈桥相遇。他们两家相距多少米？”。这个素材离学生的生活实际较远，另外，学生容易受相遇地点的干扰，认为两人走的路程是一样的，相遇地点正好在两家中间，因此改为“小红和小明同时从家出发相对而行，小红每分钟走60米，小明每分钟走70米，经过4分钟两人相遇。他们两家相距多少米？”学生易于理解，同时，具备相遇问题的关键要素，即：“同时”、“相对而行”、“相遇”、“相距”。真正做到了用教材教，而不是教教材。

2.落实两个转化，构建数学模型。

根据小学生的认知规律、年龄特点和教学内容的特征，设计了构建应用问题的数学模型的基本思路：创设问题情境，发现提出问题——建立模型准备；自主整理信息，探究解决问题——建立数学模型；解释应用拓展，体验数学价值——应用数学模型，构建了相遇问题的数学模型。在整个教学过程中，既重视“解决问题”的第一个转化：从学生的生活实际出发，创设与学生的日常生活紧密联系的情境，学生在现实而有趣的、富有挑战性的问题情境的吸引下，主动发现问题、提出问题，进而提炼生成完整的数学问题，帮助学生顺利完成解决问题的第一个转化；同时，我们也重视“解决问题”的第二个转化：即放手让学生理解关键要素——理清数量关系；借助线段图——探明解题思路；明确解题方法，独立列式解答——自主建构应用问题的数学模型，帮助学生顺利完成解决问题的第二个转化。这样，同时重视并扎实完成“两个转化”，让学生有效经历“解决问题”的全过程，从而大面积提高学生解决问题的能力，达到增强解决问题实效性的目的。

3.渗透思想方法，注重思路训练。

解决问题活动的价值不只是获得具体的结论，主要价值在于使学生初步学会从数学的角度发现问题、提出问题和解决问题；综合运用数学知识方法解决简单的实际问题；获得分析和解决问题的一些基本方法，并在此基础上形成解决问题的基本策略，掌握其思想方法。教学《相遇问题》时，着眼于学生的发展需要，根据课程标准的要求，设计了一明一暗两条线：明线是指数学基础知识和基本技能，即逐步提炼形成相遇问题，理解相遇问题的基本结构特征，并应用解决实际问题；暗线是指数学思想方法，即在解决应用问题的过程中，学生运用并形成的模拟与演示、操作与画图、分类与比较、综合与分析等解决问题的一些基本方法策略，以及数形结合、数学模型等数学思想方法。同时，注重数量关系的分析，对解题思路做必要的梳理和提炼，学生通过理清数量关系，明确解题思路，探究解题方法，引导学生对分析解决问题的过程、方法进行观察与比较、分析与综合、抽象与概括，建立了相遇问题的数学模型。